基于事件触发的大规模互联非线性系统的自适应分散漏斗控制

杨文静，夏建伟

（聊城大学 数学科学学院，山东 聊城 252000）

众所周知，大规模非线性系统通常被视为由许多相互关联的子系统组成的系统。由于控制结构的复杂性以及各子系统之间信息交换的局限性，给大规模非线性系统的控制器设计和稳定性分析带来了很大的困难。为了克服这个困难，在过去的几十年中，许多学者利用分散自适应技术控制大规模系统[1-3]。然而该控制方法有一定的局限性，即系统中的不确定非线性函数要么是参数未知的线性函数，要么是已知非线性函数。为了克服这些限制，文献[4-6]中利用神经网络或文献[7-8]中利用模糊逻辑系统来识别未知非线性函数的自适应分散控制方法得到了广泛研究。其中，在文献[8]中，针对一类具有执行器故障的非严格反馈非线性系统，利用模糊控制构造了一种改进的容错控制器，使闭环系统中的所有信号都是半全局有限时间稳定的。

另一方面， 为了有效地节省通信资源，减轻通信负担，非线性系统的自适应事件触发控制也受到了广泛的关注。与传统的时间触发控制不同，事件触发控制是一种仅在系统需要时才将控制器输出应用于系统的控制机制。最近，将模糊和神经网络逼近方法与反步技术相结合，针对具有不同触发机制的非线性系统，文献[9-14]提出了一些自适应事件触发控制方案。其中，针对具有未建模动态的随机非线性系统，文献[12]提出了一种基于变阈值方案的模糊自适应有限时间事件触发控制策略。在文献[15]中，针对一类不确定严格反馈非线性系统，设计了一种新的自适应事件触发机制，使控制器和参数估计器同时触发。然而，上述控制方案不能用于控制系统的瞬态行为和稳态性能。在许多实际应用中，除了跟踪稳定性外，经常需要系统的跟踪性能满足预定的约束条件，并要求系统达到预期的稳态跟踪精度。

最近，预定义性能控制(Predefined Performance Control， PPC)技术一经在文献[16]中提出就引起了广泛关注。预定义性能控制技术通过利用规定的性能函数(Predefined Performance Function, PPF)和构造误差变化来处理预定义的性能约束[15,17–18]。其中，文献[17]针对一类严格反馈系统，提出了一种基于有限时间性能函数的自适应模糊控制器，该控制器可以确保闭环系统的所有信号都有界，并且跟踪误差在有限时间内收敛到预定范围。然而，以上所述的基于PPF的性能控制方法取决于初始条件，这限制了其在实际中的应用。文献[19]提出了一种漏斗控制方法(Funnel Control)放宽了对初始条件的要求。近年来，利用反步技术，文献[20-21]中研究了相对度为2的非线性系统的漏斗控制问题，文献[22-24]研究了相对度大于2的非线性系统的漏斗控制问题。然而，到目前为止，对于大规模非线性系统的漏斗控制的研究还很少。因此，对于不确定大规模非线性系统，如何设计控制器，使得跟踪误差不仅在预定义的漏斗内演化，而且与初始值无关，是一个值得解决的问题。

基于上述讨论，本文研究了一类互联大规模非线性系统的自适应事件触发漏斗控制问题。本文的主要贡献如下:

(1) 与文献[15, 17-18]中基于PPF的预定义性能控制相比，本文放宽了对初始条件的约束，所提出的漏斗函数的初始值是无穷大而不是一个有界常数。

(2) 与文献[24]的研究相比，本文提出了一种新的障碍Lyapunov函数来处理漏斗约束，并确保系统的输出总是在漏斗中演化。

(3) 与文献[19-23]结果相比，利用神经网络系统、事件触发机制和反步技术设计了有限时间事件触发控制器，该控制器能有效降低控制器与执行器之间的传输负担，并大大节省通信资源。

1 问题陈述和准备工作

1.1 问题陈述

1.2 准备工作

1.3 漏斗性能

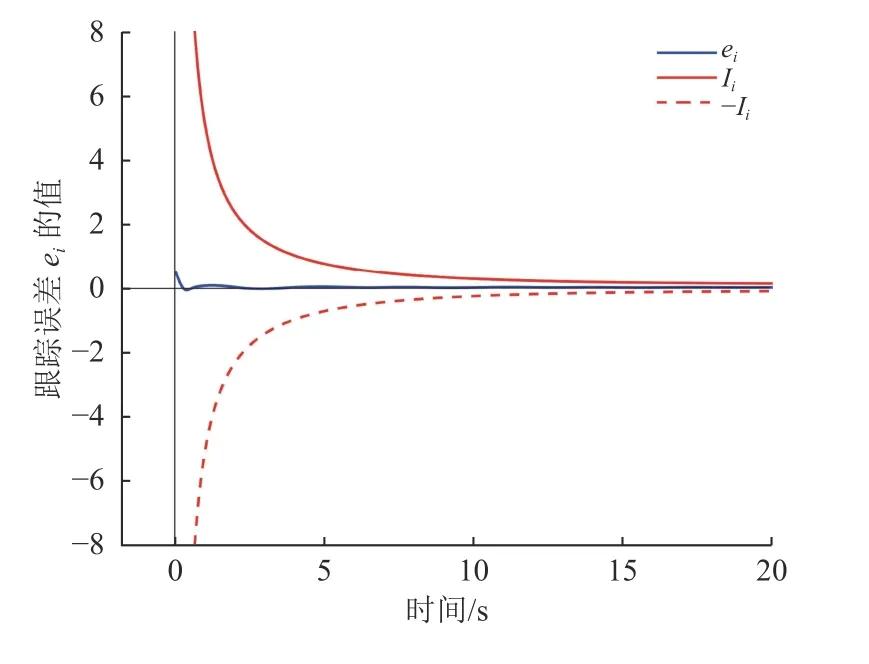
图1 跟踪误差预定性能示意图Fig.1 A diagram of the prescribed tracking behavior.

为保证跟踪误差始终在漏斗内演化，定义障碍函数为

2 事件触发控制器设计

3 稳定性分析

定理1 考虑一类具有性能约束的大规模非线性系统(1),虚拟控制器(27),事件触发控制器(29)和自适应律(44)。在假设1和假设2的条件下，可以保证以下性能：

(1) 系统的输出信号在一定误差内可以追踪到参考信号；

(2) 闭环系统中所有信号都是半全局一致有界；

(3) 跟踪误差的轨迹始终在漏斗内演变。

证明 可以通过以下4个步骤来证明定理的结果。

步骤1 对整个系统构造李雅普诺夫候选函数为

将式(55)代入式(54)得到

4 仿真

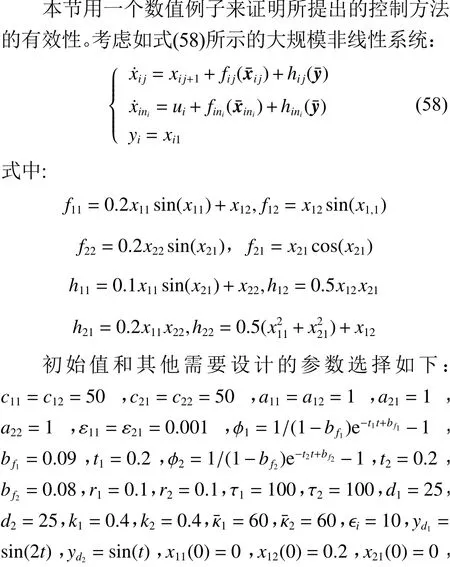
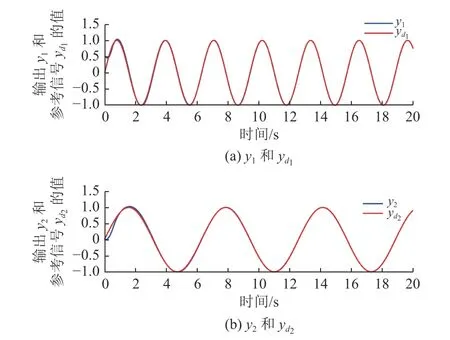
图2 y i(t)和 y di(t),i=1,2的运动轨迹Fig.2 The trajectories of y i(t) andydi(t),i=1,2

图3展示了跟踪误差ei(t)(i=1,2)的运动轨迹，从图中可以看出，跟踪误差总是在给定的区域内演化，并且所提出的控制机制放宽了对初始条件的要求。图4描述了控制器ui(t)(i=1,2)的轨迹。图5显示了触发间隔tk+1−tk。图6显示了自适应率ζ ˆi(i=1,2)的运动轨迹。

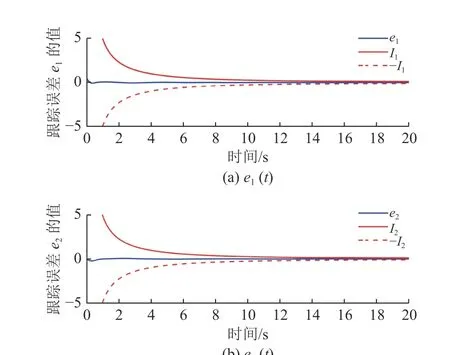
图3 跟踪误差e i(t),i=1,2的运动轨迹Fig.3 The trajectories of error trackingei(t),i=1,2

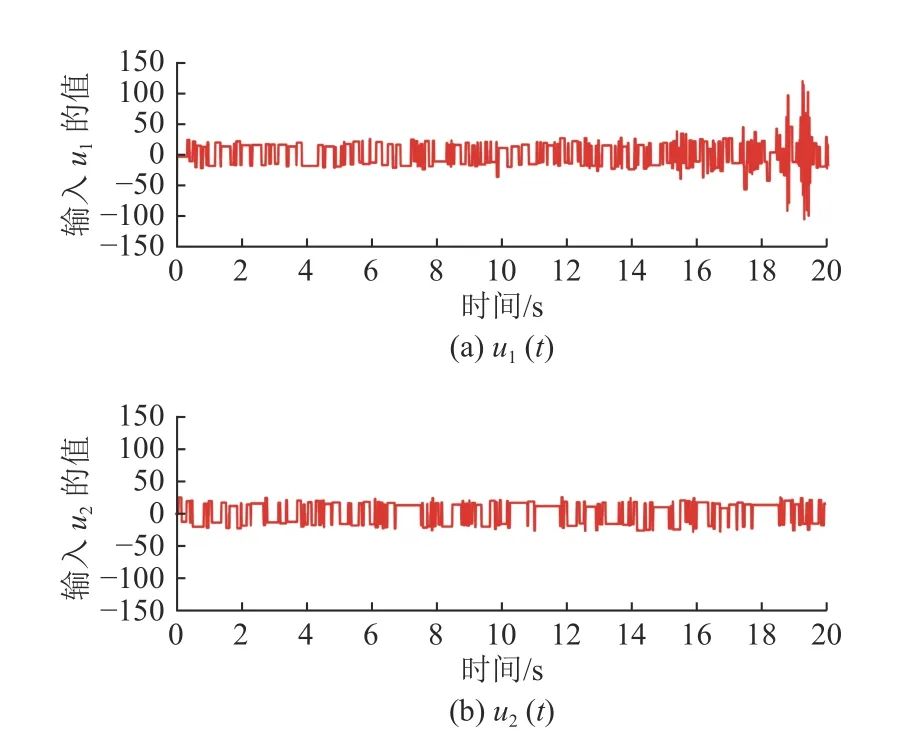
图4 u i(t),i=1,2的运动轨迹Fig.4 The trajectories ofui(t),i=1,2

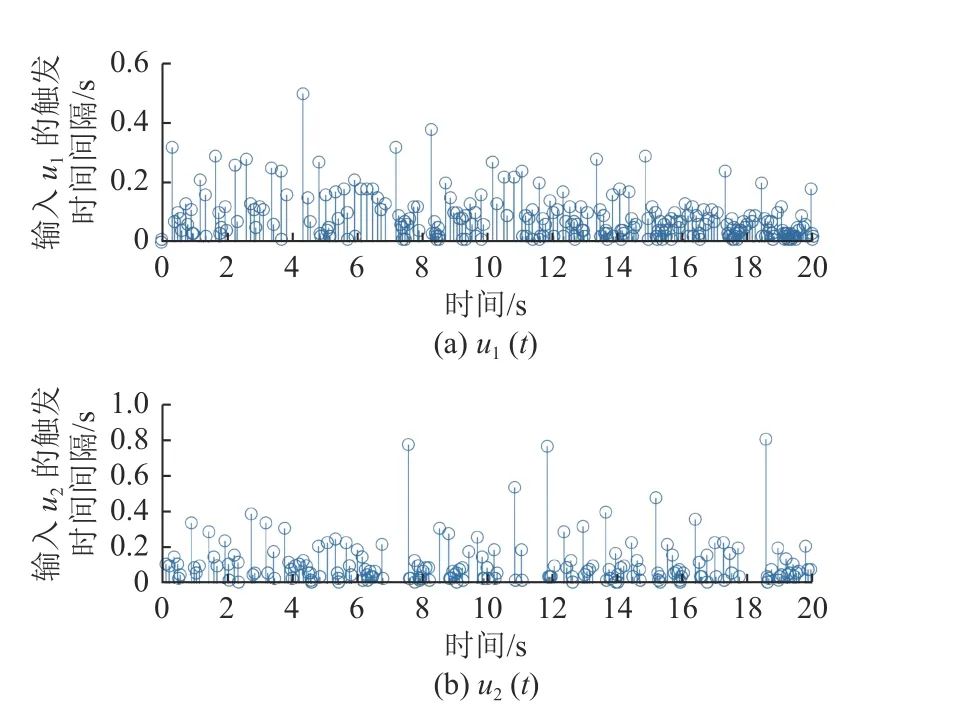
图5 u i(t),i=1,2的触发时间间隔Fig.5 Trigger time interval ofui(t),i=1,2

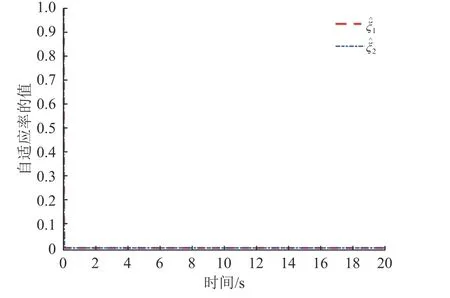
图6 自适应率ζ ˆ1和 ζ ˆ2的轨迹Fig.6 The trajectories of adaptive lawsζ ˆ1a ndζˆ2

5 结论

本文研究了一类不确定大规模非线性系统的分散自适应事件触发漏斗控制问题。首先，通过障碍李雅普诺夫函数变换，递归构造了一种新的自适应分散漏斗控制器，以实现给定瞬态行为的输出跟踪。其次，为了解决控制器设计中的互联项问题，引入了一个辅助非线性函数。同时，将命令滤波技术应用到反步设计中，避免了反步过程中的“复杂性爆炸”问题。此外，还设计了一种事件触发机制，以减少控制器和执行器之间不必要的传输，从而提高资源效率。结果表明所提出的控制方案能保证闭环系统的所有信号都是有界的，并且跟踪误差总是在漏斗中演化。最后，通过一个数值系统验证了该控制方法的有效性。