模型预测控制下多移动机器人的跟踪与避障

彭积广，肖涵臻

（广东工业大学 自动化学院，广东 广州 510006）

近些年来，移动机器人的编队控制与避障能力引起了许多研究者的兴趣，是机器人领域中非常热门的研究方向之一。基于分布式一致性的编队控制获得了快速且持续的发展，在基于一致性的编队中，由于机器人之间的通信带宽受到限制及机器人之间的信息传输应具备高质量和无延时的高标准，因此考虑机器人只能与它的邻居接收和发送信息是十分有必要的。在领导者−跟随者机器人编队形式中[1-3]，有一个及以上机器人为领导者，领导者可以是其中的某个机器人或者为虚拟机器人，它决定整个编队的运动轨迹和方向，其他移动机器人作为跟随者被领导者带领运动，并相互之间保持相对的距离与方位。文献[4]实现了一种模型预测控制(Model Predictive Control, MPC)方法来控制一个领导者−跟随者编队系统。通过在分离度−姿态−方位模型(Separation-Bearing-Orientation Scheme, SBOS)和避障模型之间进行切换，使编队避免碰撞，达到理想的编队状态，并对约束条件进行处理。但是SBOS模型难以与避障模型相结合起来。于是文献[5]提出了固定无向拓扑下基于距离与速度的人工势场方法的编队避障系统，但是没有考虑有向拓扑且拓扑可以变化下的避障，并且没考虑机器人相互避免碰撞的同时，能避免障碍物的问题。结合以上参考的工作，为在期望路径上规划机器人到达并与领导机器人保持期望距离，通过构造编队路径规划的控制输入与避障系统结合起来。

研究者们提出了许多的控制算法来控制机器人编队，如一致控制[6-7]、自适应控制[8]、滑模[9-10]和人工势场[11]等。对于群体编队，需要考虑系统约束问题。然而，模型预测控制(MPC)能够很好地考虑移动机器人的物理约束问题。另一方面，模型预测控制(MPC)方法已成功地应用于工业环境下的复杂系统的控制，是应用最广泛的最优控制技术之一。其中，文献[12-13]是一种模型预测控制(MPC)，具有轨迹优化能力，并充分考虑物理约束，适用于多机器人控制。一般来说，MPC可以解决包含约束的优化问题。在预测控制范围内，由最优解得到的输入序列总能考虑机器人的内在物理约束。为解决预测控制的优化问题，需要一种高效的优化算法。文献[14]将多机器人编队控制(General Projection Neural Network,GPNN)方法与多机器人一致编队相结合，来求解包含编队最优输入的约束(Quadratic Programming,QP)问题的最优解。与现有的领导者−跟随者方法相比，所提出的MPC方法能够考虑系统的输入约束和状态约束。本文利用投影神经网络优化算法来处理基于MPC方法的优化问题。

在实际机器人运动中，机器人处理避障的能力是十分重要的，研究者们对于这一问题进行了深入的研究[15-18]，其中一种较简单且广泛使用的避障方式为基于距离的人工势场法。人工势场法的主要思想是，当一个机器人进入其他机器人的势场中时，机器人会产生一种很强的排斥力，迫使它远离其他机器人，从而避免发生碰撞。然而，文献[19-20]中的人工势场方法仅基于机器人之间的距离进行设计，在很多情况下具有相当大的局限性。例如：一机器人虽然进入势场中，但是两机器人的移动方向和速度不同，使得机器人之间不会产生碰撞，此时，机器人也会因靠近产生排斥力，从而会增加机器人的能量消耗，并且易致编队控制不稳定。机器人也需有避开障碍物的能力，运用人工势场法来进行避障处理。基于上述分析，本文利用一种基于距离和速度的人工势场方法来处理多移动机器人编队控制的机器人间的避碰问题和人工势场法来处理避免障碍物。

受以上文献启发，本文首次将文献[5]的基于距离与速度的人工势场方法引入有向拓扑且拓扑可以变化下考虑机器人相互避免碰撞避障。同时，运用人工势场法[21]能避免障碍物的问题，且融合进一阶多移动机器人的一致性编队路径规划控制中。本文提出两层编队控制框架， 在编队控制层面上，设计具有避碰的编队控制律控制。可以使机器人在相对平滑的轨迹上运动且具有避障能力，并与相邻机器人达到并保持预期的距离。在编队跟踪层，应用GPNN结合MPC方法重构并求解一个基于跟踪误差模型的约束QP问题。得到控制机器人的最优输入，同时考虑速度约束和系统状态约束。该两层群形成框架综合了轨迹生成方法和算法的优点。

1 预备知识及问题描述

1.1 代数图论

1.2 问题描述

2 一致性控制编队避障控制律

在实际工作过程中，机器人的避障能力是十分必要的，不仅仅是避免对障碍物的碰撞，而且机器人相互之间也需要有良好的避障能力。对于基于距离的人工势场法的避障系统，当某一机器人进入另一机器人的势场范围内或两个及以上机器人的势场范围发生接触时，机器人之间就会迅速产生排斥力。但是如图1所示，即使其进入势场的范围内时，机器人之间也不会发生碰撞。此时机器人之间的碰撞不仅仅取决于机器人之间的距离，也与机器人之间的速度的大小和方向相关。根据文献[5]，可用基于距离和速度的避障方式来建立机器人躲避障碍的模型。

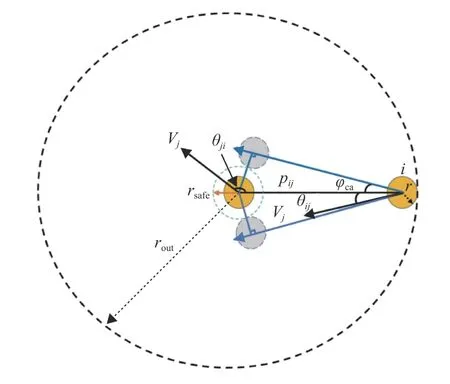
图1 基于距离与速度的机器人避障图Fig.1 Obstacle avoidance diagram of robot based on distance and speed

3 移动机器人编队跟踪系统

3.1 编队跟踪误差模型

3.2 模型预测控制策略

为了控制编队跟踪良好，采用MPC方法。在有限时间范围之类，经过欧拉离散化的系统，可转化为具有输入和状态饱和约束以及离散非线性模型方程的闭环离散时间最优控制问题。因此，将系统的控制输入和状态方法转化成离散时间状态空间方程。编队控制目标、避障实现和轨迹跟踪可以通过MPC方法转化为离散时间闭环优化控制问题。不失一般性，可得到广义非线性离散仿射系统：

模型预测控制是一种基于模型的闭环优化控制策略，其算法的核心是:可预测未来的动态模型，在线反复优化计算并滚动实施的控制作用和模型误差的反馈校正。因此，对比于传统或经典的控制器，模型预测控制具有控制效果好、鲁棒性强等优点，可有效地克服过程的不确定性、非线性和并联性，并能方便地处理被控变量和操纵变量中的各种约束。因此，代价函数可表示为

3.3 广义投影神经网络优化

为了在线模型预测控制中获得已规划的优化问题的最优解，需要寻求一种高效的最优化方法来求解。因此，一种广义投影神经网络优化的方法被提出。为了解决二次规划问题(19)，开发了一种单层结构一般投影神经网络(GPNN)，它是一种递归神经网络(Recurrent Neural Network, RNN)。广义投影神经网络是一类求解更广泛的单调变分不等式和相关的优化问题。本文所提出的神经网络具有低模型复杂度的单层结构，包含了现有的用于约束优化的神经网络，如原始对偶神经网络、对偶神经网络和投影神经网络，均为广义投影神经网络的特殊情况。广义投影神经网络的渐进神经网络的递归神经网络(RNN)用于解 MPC 控制中产生的二次规划问题，并表现出了较低的计算复杂度。通过GPNN方法，可得到具有全局指数收敛性和李雅普诺夫稳定性的二次规划问题最优解。因此，有以下定理[20]：

4 仿真

在本节中，利用Matlab对一组编队的非完整移动机器人进行轨迹跟踪和避障仿真，以验证本文提出的避障与轨迹跟踪的控制性能和有效性。本文以3个机器人和1个虚拟机器人为例进行数值计算。机器人被标记为R1～R3， 虚拟领导者被标记为RL。

在本文中，图2为机器人的通信拓扑结构，在机器人运动过程中可选用两种通信拓扑。实验1仿真结果如图3～图7所示。在图3中，跟随者可以实现并保持所期望的直线运动的规则三角形，跟随者的几何中心可以跟踪领导者的轨迹。并且跟随者即实际机器人可以实现良好的避障效果。与文献[5]相比，本文不仅实现了良好的避障而且可以进行编队控制与跟踪。在图4～图5中显示了机器人的线速度和角速度的变化，可以看到线速度和角速度受到约束。图6～图7中，通过使用的一致性控制方法，所有的一致性误差都可以稳定到原点。

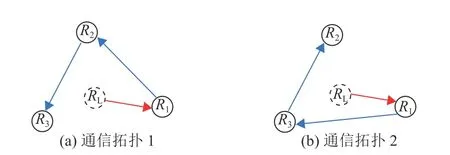
图2 通信拓扑结构图Fig.2 Communication topology

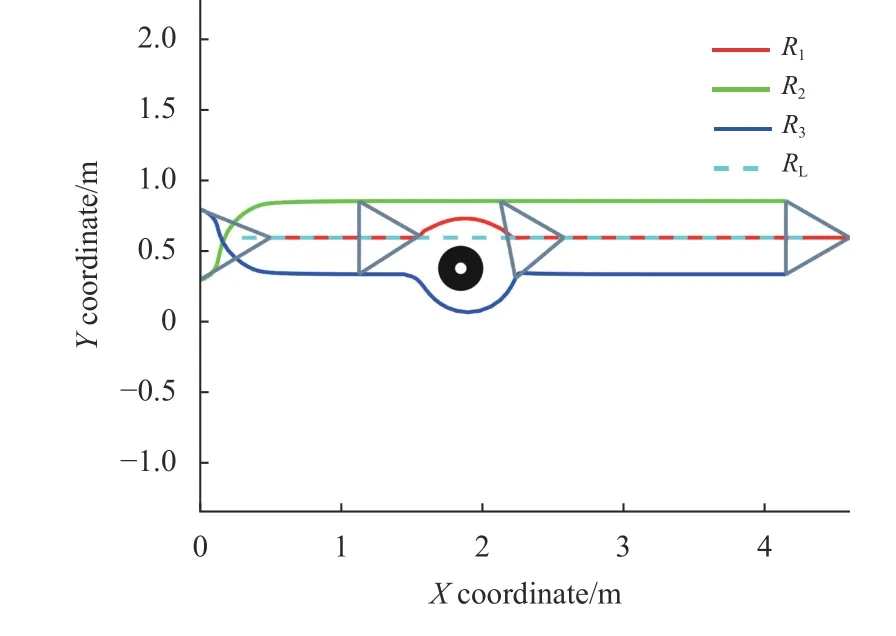
图3 实验1编队的跟踪与避障Fig.3 Formation tracking and obstacle avoidance in test one

图4 实验1机器人Ri 的线速度Fig.4Linear velocitiesofRiintest one

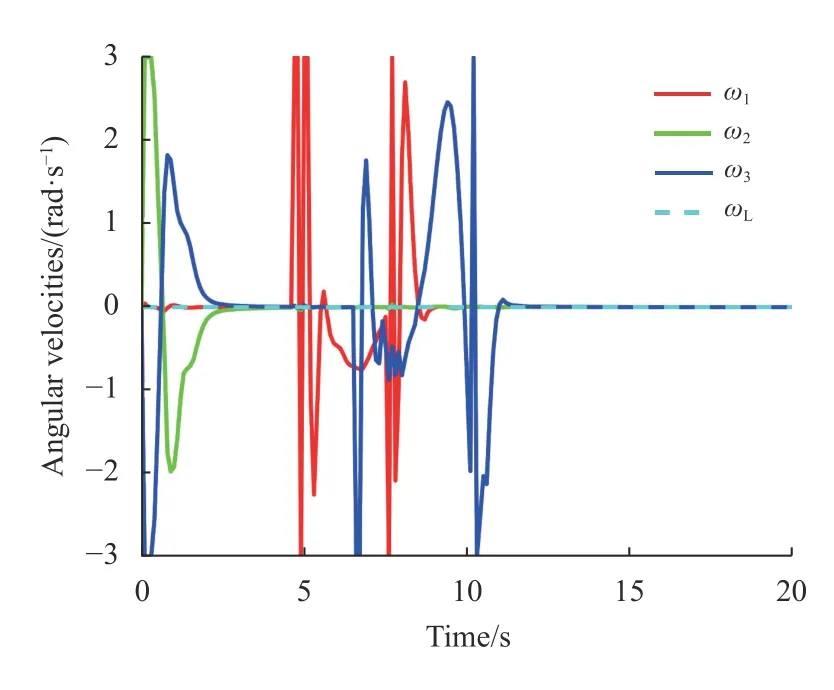
图5 实验1机器人Ri 的角速度Fig.5Angularvelocities of Riin test one

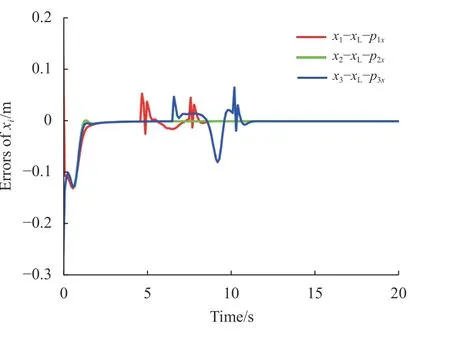
图6 实验1 xi的误差演化Fig.6 Evolutions of errorsofxiin test one

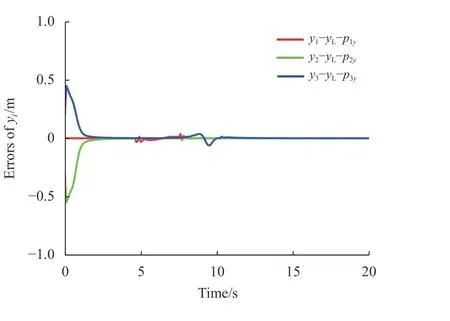
图7 实验1yi的误差演化Fig.7 Evolutions oferrorsofyiin test one

实验2仿真结果如图8～图12所示。在图8中，跟随者可以实现并保持所期望的正弦曲线的规则三角形运动，跟随者的几何中心可以跟踪领导者的轨迹。并且跟随者即实际机器人可以实现良好的避障效果。在图9～图10中显示了机器人的线速度和角速度的变化，表示线速度和角速度受到约束。图11～图12中，通过使用的一致性控制方法，所有的一致性误差都可以稳定到零或趋于零。综合上述仿真结果表明:采用所提出的控制策略，本文系统能够在充分考虑输入约束的前提下实现编队跟踪目标与避障处理。通过上述实例，验证了该控制方法系统的有效性。

图8 实验2编队的跟踪与避障Fig.8 Formation tracking and obstacle avoidance in test two

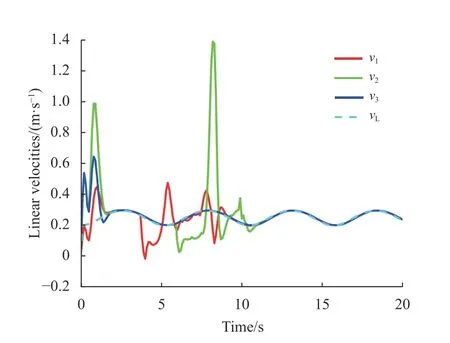
图9实验2机器人Ri 的线速度Fig.9Linear velocitiesofRiintest two

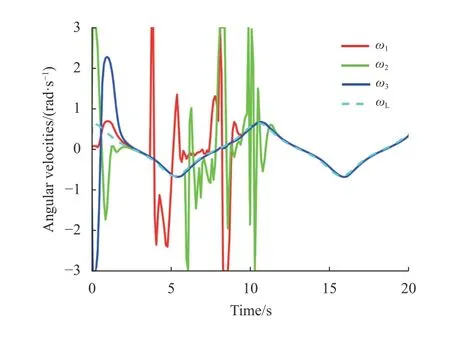
图10实验2机器人Ri 的角速度Fig.10Angularvelocities of Riin test two

图11 实验2 xi 的误差演化Fig.11 Evolutions of errorsofxiin test two

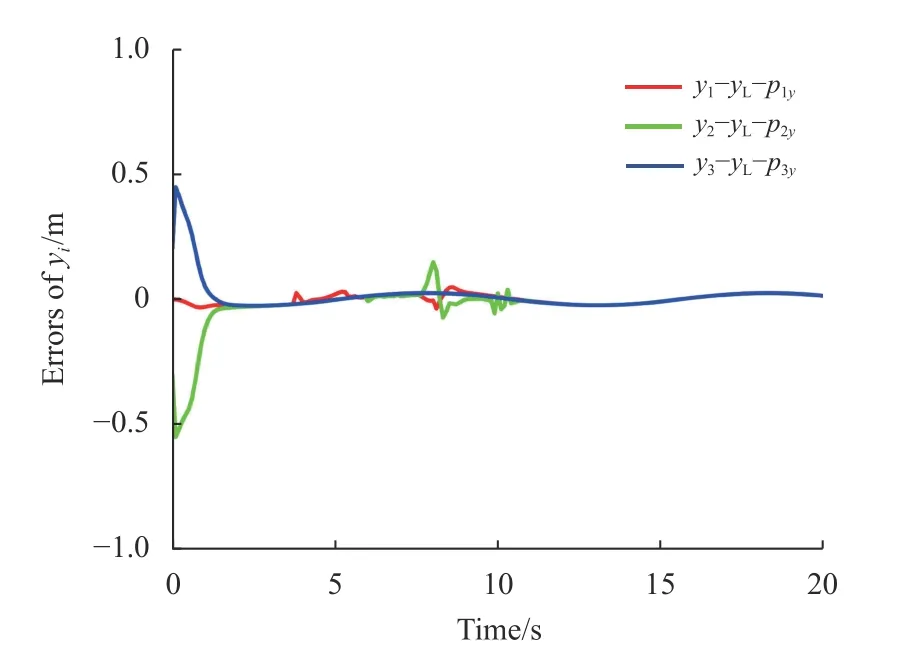
图12 实验2yi的误差演化Fig.12 Evolutions oferrorsofyiin test two

5 结论

本文研究了在虚拟领导者下的具有一阶多移动机器人系统在基于位移与速度下的一致性编队跟踪与避障控制问题。首先设计多机器人的通信拓扑，再设计具有避障功能的一致性编队控制律，然后设计移动机器人编队跟踪系统，运用模型预测控制(MPC)方法，将编队误差运动问题按代价函数转化为最小优化问题。利用广义投影神经网络优化的方法求解最优值。本文给出的理论分析和仿真结果验证了该方法的有效性。