基于扩张状态观测器的永磁同步电机转速环连续螺旋控制

吴 宜，梅珂琪，丁世宏，葛群辉，王巍植

（1. 江苏大学 电气信息工程学院，江苏 镇江 212000；2. 德玛克 (长兴) 注塑系统有限公司，浙江 湖州 313100）

永磁同步电机(Permanent Magnetic Synchronous Motor, PMSM)具有可靠、高效、损耗小等优点，在许多工业应用中起着至关重要的作用。然而，在传统线性控制方法下，很难满足PMSM系统的控制性能要求。原因在于，传统控制方法难以处理外部扰动、参数扰动和非线性动力等不确定性问题[1-5]。因此，越来越多的研究学者开始关注PMSM的非线性控制策略，进而提出了很多控制方法，如模糊控制[6]、鲁棒控制[7]、自适应控制[8]、滑模控制(Sliding Mode Control，SMC)[9-13]等。

在这些方法中，滑模控制因其较强的抗干扰能力而广受关注。其主要优点是，当系统的状态轨迹进入滑动阶段时，它可以有效地抑制参数扰动和外部扰动的影响。为了进一步提高电机的性能，文献[14]提出了一种积分滑模控制(Integral Sliding-mode Control，ISMC)，并将其用于PMSM的速度调节。虽与SMC相比，ISMC提高了系统的动态响应性能，但ISMC也存在不连续控制项，这导致了抖振现象，并限制了系统的性能。为了有效地抑制抖振，文献[15]提出了一种连续螺旋算法。该算法可以使系统状态在有限时间内稳定到原点，并显著地减少系统的抖振，但控制器的高开关增益会影响系统性能。于是在文献[16]中提出了一种新型ESO，解决了控制器的高开关增益问题，并且在一定程度上提高了PMSM的控制精度与鲁棒性。

为了综合地解决上述PMSM存在的抖振以及控制器增益过大的一系列问题，本文在文献[14-17]的基础上提出了一种基于ESO的连续螺旋滑模控制(CTSMC)方法。本文的主要贡献可以概括为两个方面。一方面是针对期望速度和实际速度之间的误差过大的问题，提出CTSMC。与比例积分(Proportional Integral，PI)控制相比，该控制可以将误差收敛到一定的区域，从而确保PMSM调速系统具有很强的跟踪性能[18-20]。另一方面是针对CTSMC的高开关增益会带来较差动态性能的问题，提出了一种ESO来估计系统的扰动，从而避免了上述的问题，并且进一步增强了系统的鲁棒性[21-24]。

1 PMSM矢量控制数学模型

式中：ud、uq分别为d、q轴电压；φf为电机的磁链；id、iq分别为d、q轴电流；ω 为电角速度；Rs为定子电阻；TL为负载转矩；J为转动惯量；B为摩擦系数；Ls为定子电感；np为极对数。

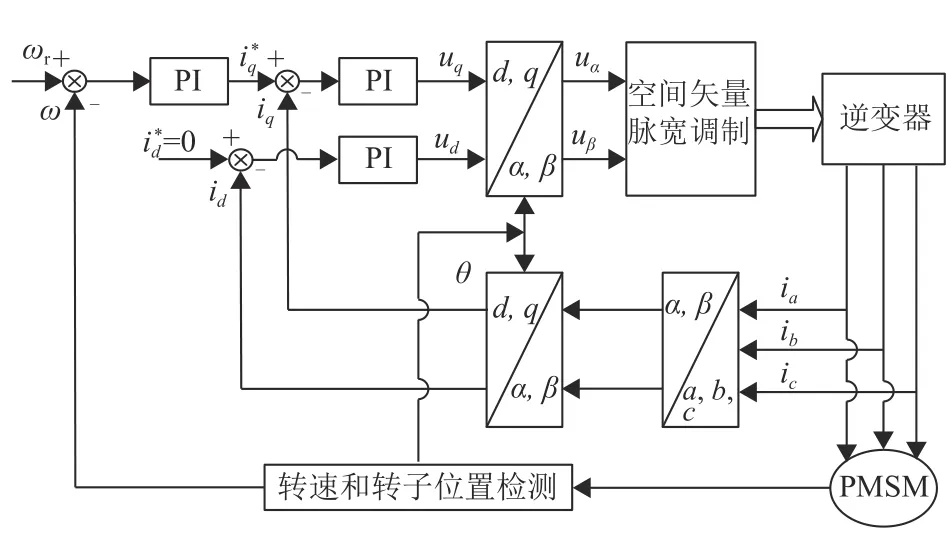
图1 id=0永磁同步电机矢量控制框图Fig.1 Vectorcontrolblockdiagramof PMSMwithid=0

2 PMSM转速环控制器设计

从以上分析可以看出，状态模型是控制设计的基础。传统PMSM的速度调节器使用速度PI控制器来产生相应的参考电流。然而，当负载发生突变以及内部参数发生扰动时，PI控制器的性能并不理想[28-29]。SMC具有对外部干扰和参数扰动不敏感、强鲁棒性和快速响应等优点。因此，提出了一种CTSMC，能够为PMSM的调速提供快速准确的参考输入。此外，CTSMC还可以进一步提高系统的性能和收敛速度。

2.1 CTSMC设计

PMSM系统的主要控制目标是在有负载扰动的情况下提高系统的跟踪精度。将调速系统的跟踪误差定义为

根据此表达式可以证明定理2。

2.2 基于ESO的转速环复合控制器设计

为了提高系统的抗干扰能力和收敛速度，在速度系统中设计了一个观测器。在本节中，首先建立了一个ESO，用来估计PMSM调速系统的扰动。然后，将CTSMC与ESO的估计值相结合，构成复合控制器。

首先，对转速环设计二阶ESO，可表示为

然后，结合之前构建的CTSMC，得到复合控制器。

综上所述，基于ESO的永磁同步电机CTSMC控制原理图如图2所示。

图2 基于ESO的永磁同步电机连续螺旋控制原理图Fig.2 Principle diagram of CTSMC of PMSM based on ESO

3 仿真与实验

为了证明所提出控制器的有效性，在永磁同步电机系统上完成了PI控制器和CTSMC的仿真和实验。该平台采用的是型号为130ST-M10015的三相电机和RTU-BOX204实时数字控制器。系统参数如表1所示。

表1 电机驱动参数Table 1 Motor drive parameters

3.1 仿真结果

本文采用id=0的矢量控制，为了公平，可以任意调整所提出控制器的参数，以实现其最佳性能。CTSMC的开关增益选择为λ1=3.5、λ2=0.5、λ3=0.23和 λ4=0.11。此外，无论在速度回路中使用哪种控制器，仿真中两个电流回路的PI控制器参数都是相同的。比例和积分增益分别为20和1 500。参考转速为500 r/min。为了验证所提出控制器的抗干扰性能，本文考虑了负载转矩变化(2.4 N·m)。3种控制方法在负载突变情况下的仿真结果如图3～5所示。从图3～4中可以看出，PI控制器的抗超调能力比CTSMC的差，且CTSMC控制策略在稳定性和抗干扰性能方面优于PI方法。此外，在CTSMC+ESO控制下，电机明显具有更好的抗负载性能。从图5中可以看出，在起动阶段，与CTSMC相比PI控制器的启动电流明显过大。

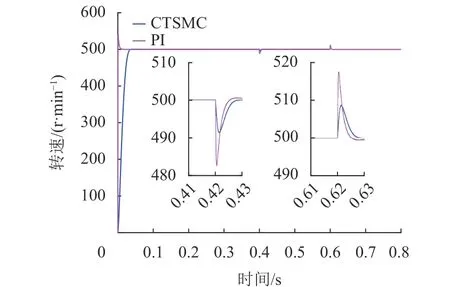
图3 仿真中PI控制器和CTSMC的转速响应对比Fig.3 Comparison of PI controller and CTSMC speed response in the simulation

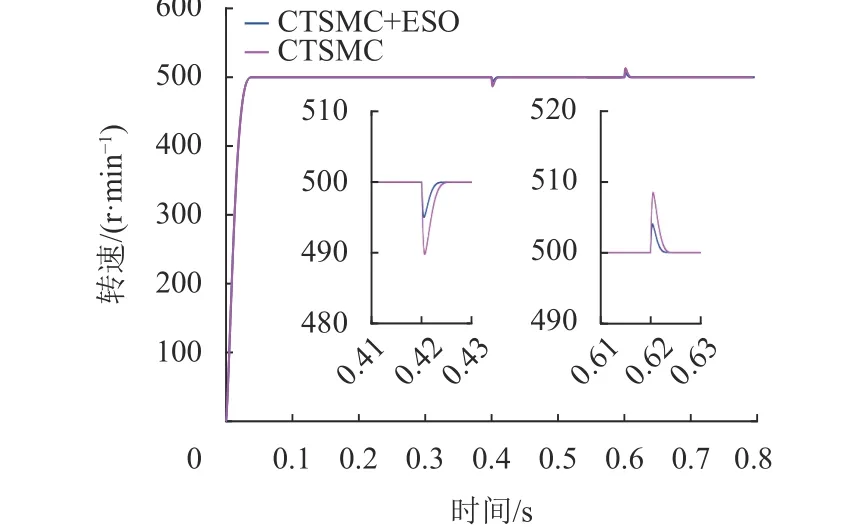
图4 仿真中CTSMC+ESO和CTSMC的转速响应对比Fig.4 Comparison of CTSMC+ESO and CTSMC speed response in the simulation

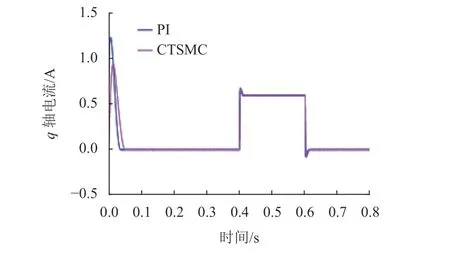
图5 PI控制器和CTSMC的 q轴电流响应对比Fig.5 Comparison of CTSMC and PI controller current response of axis of q

3.2 实验结果

为了进一步研究CTSMC+ESO控制器的有效性，进行了一些实时实验。将ESO和CTSMC应用于PMSM的调速问题以提高系统性能。电流回路的PI控制器的参数同步选择为比例增益0.05和积分增益3000。此外，控制器的参数与仿真中的参数相同。

首先比较了PI控制器和CTSMC的系统性能。两者的参数与仿真中的参数相同。电机在500 r/min的转速并且无负载的条件下，实验结果如图6～7所示。从图6～7可以看出，CTSMC无论在转速还是电流上都表现出更小的超调量和更好的抗干扰性能。

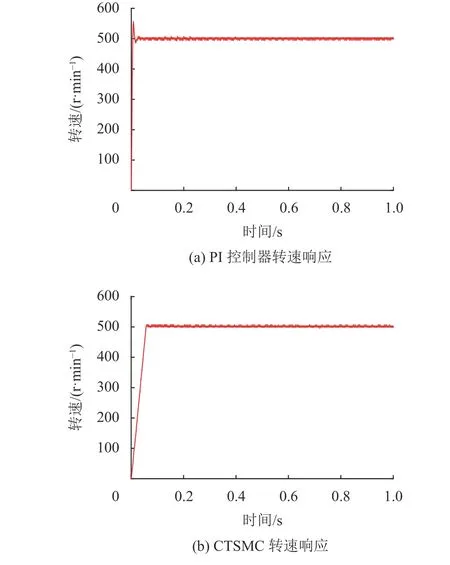
图6 实时实验中PI控制器和CTSMC的转速响应对比Fig.6 Comparison of PI controller and CTSMC speed response in the real time experiment

为了验证加了ESO系统后的性能，对PI控制器、CTSMC和ESO+CTSMC在突加负载下的系统性能进行了比较。从图8～10中可以看出，当添加干扰负载时，可以观察到CTSMC下永磁同步电机系统的转速响应波动较小，并且虽然ESO+CTSMC具有较小的开关增益，但它的最大转速波动远小于CTSMC的最大转速波动。此外，可以很容易地观察到，CTSMC以及ESO+CTSMC下的a相电流和q轴电流波动有所减小。

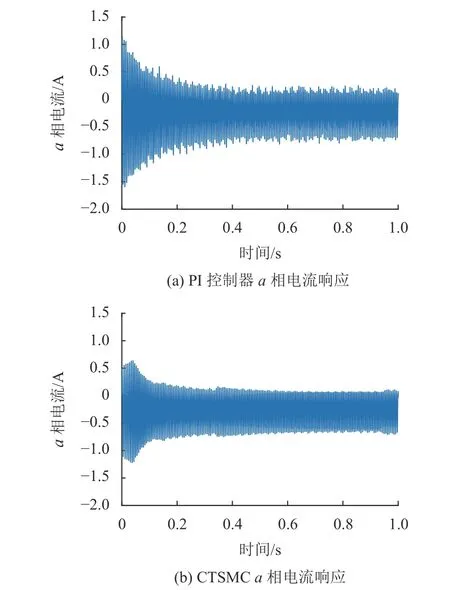
图7 PI控制器和CTSMC的 a相电流响应对比Fig.7 Comparison of PI and CTSMC current response of phase a

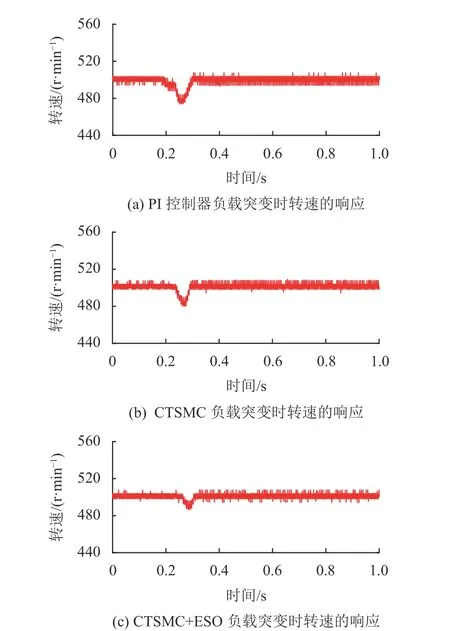
图8 负载突变时转速的响应对比Fig.8 Comparison of speed response under sudden load change

图9 负载突变时a相电流的响应对比Fig.9 Comparison of current response of phase a under sudden load change

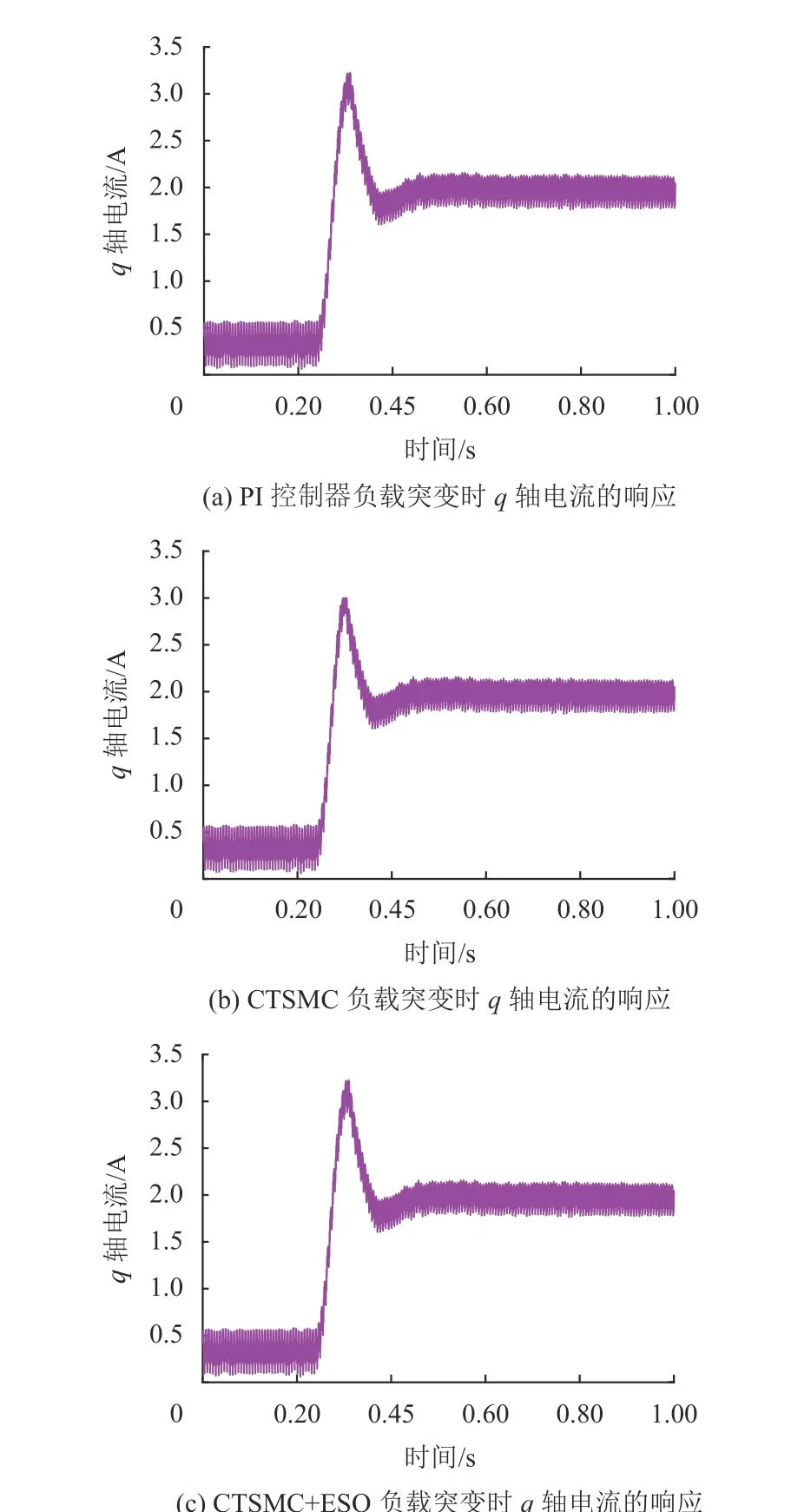
图10 负载突变时q轴电流的响应对比Fig.10 Comparison of current response of axis of q under sudden load change

4 结论

本文介绍了一种基于ESO的复合连续螺旋滑模控制方案在永磁同步电机系统中的应用。首先在转速环部分采用CTSMC方法，提高了负载扰动的鲁棒性，有效减少了系统的抖振。其次，在此控制器的基础上加入ESO，利用CTSMC和ESO的前馈补偿构造复合控制器，可以避免开关增益过高导致的动态性能不理想问题。最后，仿真和实验结果都验证了CTSMC+ESO控制器的有效性。未来的工作可以在控制器设计中采用自适应连续螺旋控制算法，使控制器自动地调节增益。