扩展的(3+1)维浅水波方程的解析解
2022-07-23刘会彩李东方
刘会彩,李东方
(许昌电气职业学院公共教学部,河南 许昌 461000)
对非线性可积方程的研究正蓬勃发展,因为这些方程可用来描述海洋学、大气领域和工程等领域的真实特征。这促使科学家们投入更多的工作来寻找非线性可积模型的解析解,如孤子解[1-8],在理解非线性科学现象的各种定性和定量特征方面起着重要的作用。而最近几十年,浅水波方程一直是广大研究人员研究的热点。浅水波方程是一种水深远小于自由水面扰动的波长的模型。各种浅水波模型在海洋和大气场中被广泛地用于模拟水波传播的动力学行为,比如:
(2+1)维浅水波方程
uxxxy+uyt-3uyuxx-3uxuxy=0
(1)
和
uxxxy+uxt-2uyuxx-4uxuxy=0
(2)
(3+1)维浅水波方程
uxxxyz+uyzt-6uxyuxz-6uxuxyz=0
(3)
和
uxxxyz+uxzt-2(uxxuyz+uyuxxz)-4(uxuxyz+uxzuxy)=0
(4)
本文将讨论一个新的扩展的(3+1)维常系数浅水波方程[9]
uxxxy+uyt+αuxx+βuyy+γuxy+δuyz-3uyuxx-3uxuxy=0
(5)
其中u=u(x,y,z,t),α,β,γ和δ是常数。这个方程是Abdul-Majid Wazwaz首先提出来的。他使用Painlevé分析证明了这个新发展的方程(5)具有可积性,给出了受参数α,β,γ和δ以及附加项系数影响的明显色散关系。该作者还获得了方程(5)的多孤子解和lump解。方程(5)其他的解析解尚未看到文献研究过。
做变换u(x,y,z,t)=-2[lnξ(x,y,z,t)]x,可得方程(5)的Hirota双线性形式
(6)
或者
(7)
事实证明,方程(6)和(7)的解是相同的。
2 解析解
为了获得方程(7)的解,不妨设
ξ=e-xλ11-yλ12-zλ13-tλ14+exλ11+yλ12+zλ13+tλ14φ1+φ2tan(xλ21+yλ22+zλ23+tλ24)+φ3tanh(xλ31+yλ32+zλ33+tλ34)
(8)
其中φi和λij(i=1,2,3;j=1,2,3,4)是待定常数。将方程(8)代入方程(7)可得:

(9)
将方程(9)代入方程(8)和变换u(x,y,z,t)=-2[lnξ(x,y,z,t)]x中可得方程(5)的第一组新的解析解
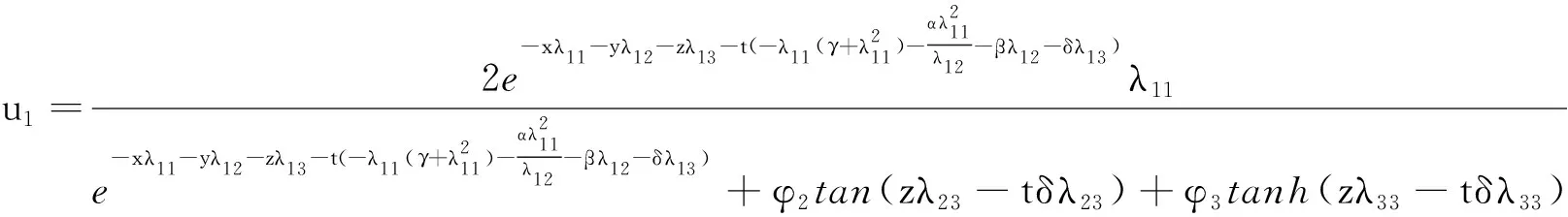
(10)
为了了解方程(10)的动力学行为,我们给出了相应的三维图形(a)、等高线图(b)以及密度图(c)(见图1)。
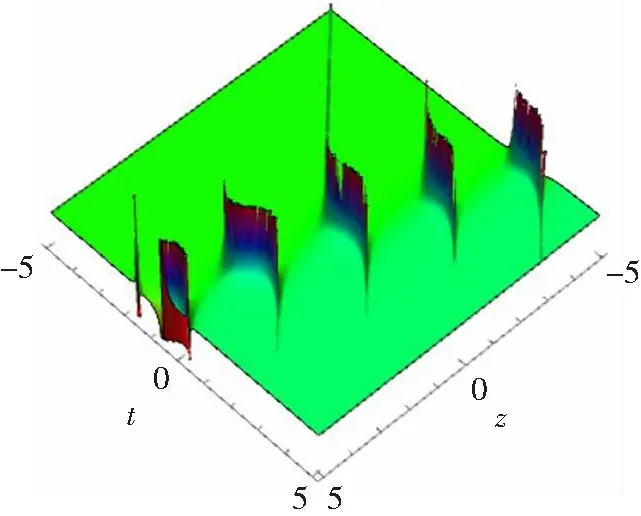
(a)
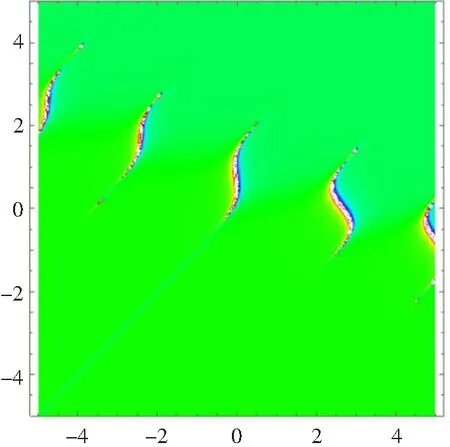
(b)
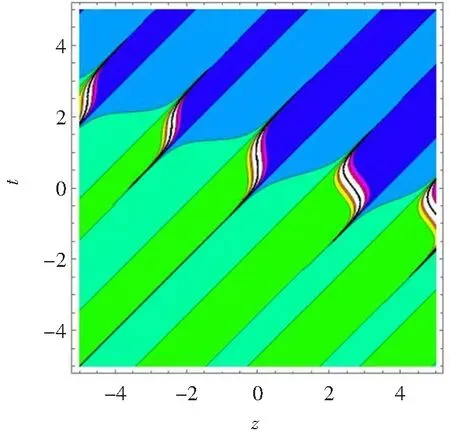
(c)图1 λ11=λ12=λ23=δ=γ= α=β=φ3=x=y=1,λ13=-1,φ2=2
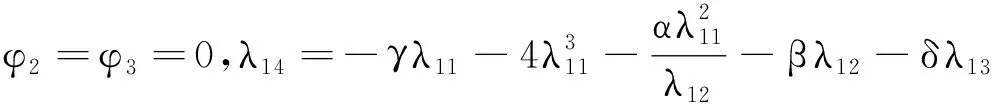
(11)
将方程(11)代入方程(8)和变换u(x,y,z,t)=-2[lnξ(x,y,z,t)]x中可得方程(5)的第二组新的解析解
u2=-2(-
(12)
为了了解方程(12)的动力学行为,我们分别给出了(z,t)平面(a)、(y,t)平面(b)以及(x,y)平面(c)下的三维图形(见图2)。
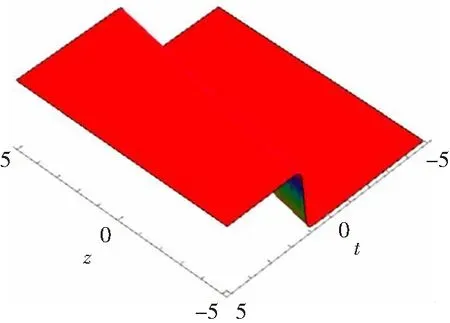
(a)

(b)

(c)图2 λ11=λ12=δ=γ=α= β=x=y=1,λ13=-1,φ1=2
(3)φ2=λ32=λ12=α=0
(13)
将方程(13)代入方程(8)和变换u(x,y,z,t)=-2[lnξ(x,y,z,t)]x中可得方程(5)的第三组新的解析解
(14)
为了了解方程(14)的动力学行为,我们给出了相应的三维图形(a)、等高线图(b)以及密度图(c)(见图3)。

(a)
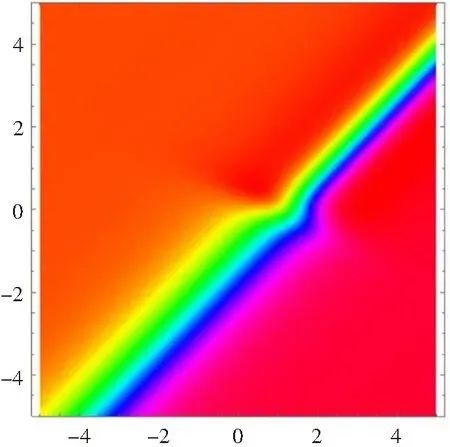
(b)
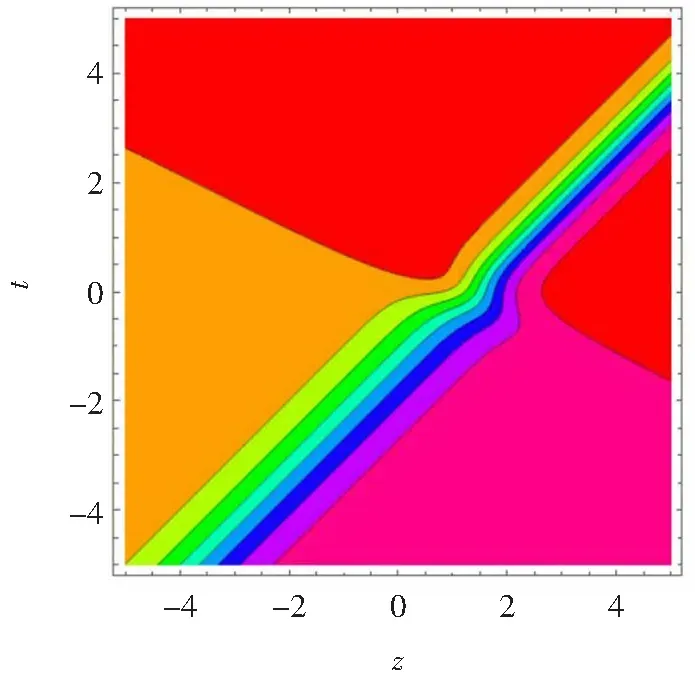
(c)图3 λ11=λ14=λ31=φ3=x=y=1, λ13=λ33=-1,φ1=2,λ34=-2
(4)φ3=λ22=λ12=α=0
(15)
将方程(15)代入方程(8)和变换u(x,y,z,t)=-2[lnξ(x,y,z,t)]x中可得方程(5)的第四组新的解析解
(16)
为了了解方程(16)的动力学行为,我们给出了相应的三维图形(a)、等高线图(b)以及密度图(c)(见图4)。
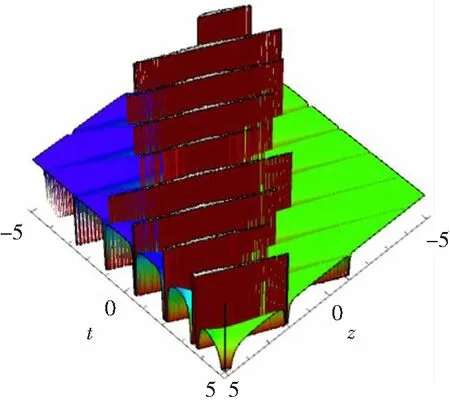
(a)
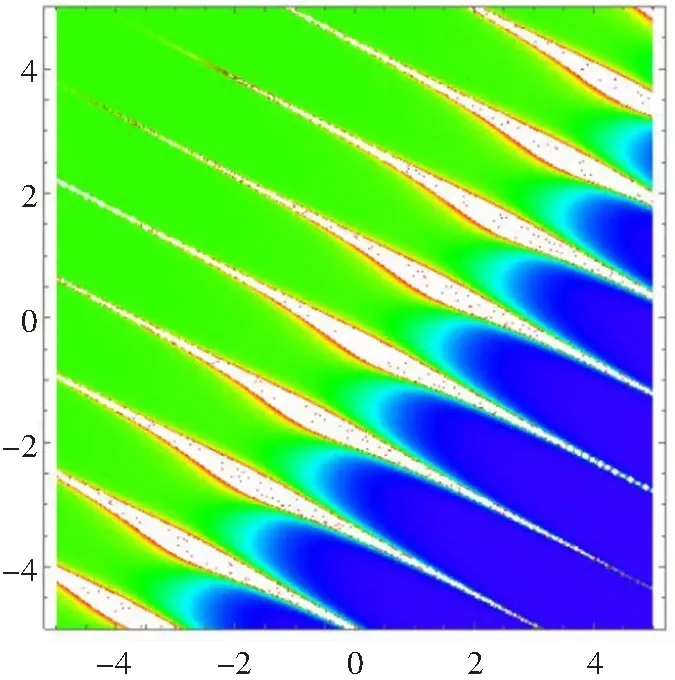
(b)
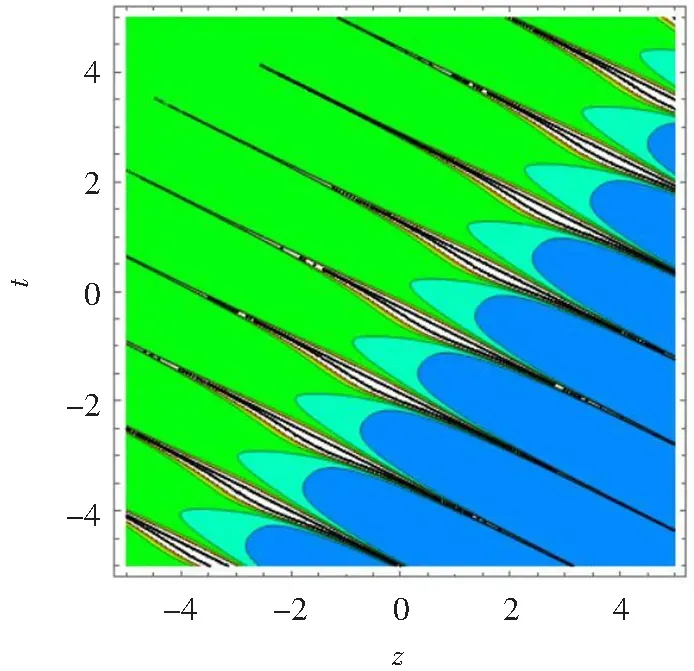
(c)图4 λ11=λ14=λ21=φ2=x=y=1,λ13=λ23=-1,φ1=2,λ24=-2
3 结论
高阶非线性可积方程能够用来描述更为真实复杂的现实模型,研究这些方程的解析解是非常有意义的,目前已经有很多方法被提出来,比如:G’/G-展开式法、双曲函数法、Hirota双线性方法、三波法等等。本文主要通过Hirota双线性方法和一个特定的函数,获得了一个新的扩展的(3+1)维常系数浅水波方程的四组新的解析解,并对这些解的动力学行为进行了展示和分析。这些解有助于我们理解水深远小于自由水面扰动的波长的模型。
