基于支持向量机和PCA 的脑电α 波运动想象分类研究

蔡 靖 ，刘光达 ，王尧尧 ，宫晓宇

（1.吉林大学 仪器科学与电气工程学院，吉林 长春 130012；2.吉林大学 教育技术中心，吉林 长春 130061）

0 引言

脑电信号EEG 是大脑中神经元产生的生物电[1]，不同的运动想象活动中，大脑释放不同的脑电信号[2]。脑电波按频率大小分为五大类：α波（8～14 Hz）、β波（14～30 Hz）、θ波（4～8 Hz）、δ波（4 Hz 以 下）和γ波（30 Hz 以上）[3]。本文对脑电信号进行小波分解并提取α波[4]，计算α 波的多个信号特征，利用PCA 技术筛选出强相关特征量，运用支持向量机进行运动想象分类[5]。通过实验发现运用小波包变换和PCA 技术后的分类准确率明显提高。

1 基本原理和算法

1.1 小波包分解

小波包分解以尺度函数φ（t）和小波函数ψ（t）为基函数进行[6]，两者的二尺度关系为：

式中，h0k、h1k是滤波器系数。小波基为：

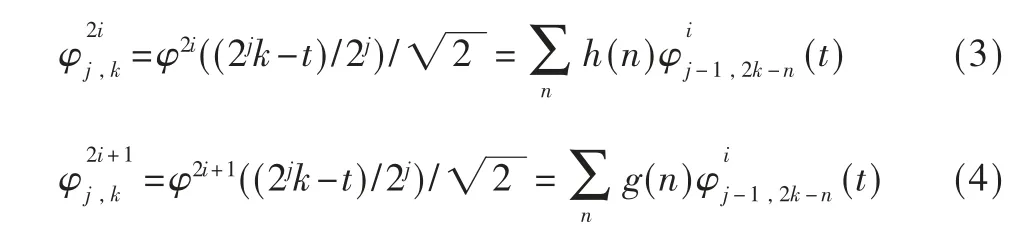
其中：i 表示节点号，j 表示分解级数；设f（t）表示时间信号，（t）是小波包系数，表示第j 层上的第i 个小波包。小波包分解的算法为[7]：

1.2 主成分分析（PCA）原理与算法

如果将n 维空间中的n 个样本x1，x2，…，xn看成一个n 维随机变量，其矩阵的形式为X=[x1；x2；…；xn]，对X 的所有列取平均，得：

其中，n 表示样本的总数，m 表示样本的均值[8]。样本集X 对应的协方差矩阵St：

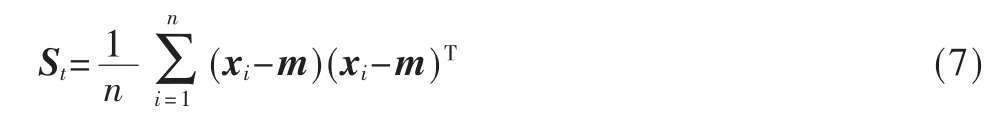
对一个n 维随机变量xi，经过以下变换：

得到一个新的n 维变量yi，其矩阵形式为Y=[y1，y2，…，yn]T，其中W 为投影矩阵。将这一组变量带入下式便可以重构出原始数据：

1.3 支持向量机（SVM）原理与算法

若数据样本可以被一线性函数分开，则其为线性可分的，称该函数为超平面[9]：

其中，x+和x-分别表示两个正负支持向量。SVM 的思想是将间隔最大化，即：

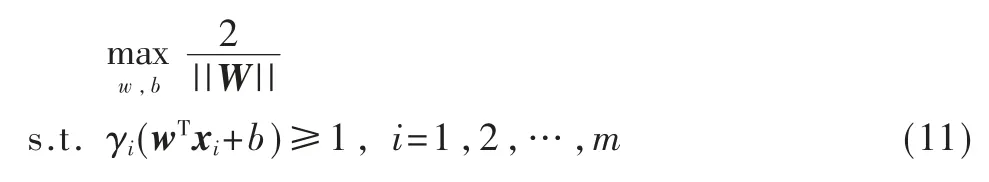
此公式即为支持向量机。

2 脑电信号特征波提取与分类

2.1 小波包分解方法提取α 波

由于α 波处于8～13 Hz 频段[10]，频率分辨率很难满足提取的要求，因此本文采用db7 小波对脑电信号进行7 层分解。

2.2 特征提取

2.2.1 均值

对α 波数据求其均值，计算均值如式（13）所示：

其中，N 为样本点个数。

2.2.2 标准差对α 波信号求其方差，如式（14）所示：

2.2.3 最值

对α 波数据提取最大值和最小值作为两个特征进行提取，计算公式如下：

2.2.4 中位数

对α 波数据提取中位数作为特征进行提取，计算公式如下：

2.2.5 功率谱

本文采用周期图法求整体功率谱密度，其核心是傅里叶变换。由式（3）知，要得到功率谱密度，需要求得功率，通过坐标变化可得功率谱密度。而通过对采样信号做傅里叶变换，可以得到离散点的幅度，再通过功率和幅度之间的关系，便可得到功率：

2.2.6 能量谱密度

通过傅里叶变换，将能量信号分离为不同频域分量所对应的能量，通过对ω 积分得到信号的总能量，由此，|X（ω）|2便可定义为能量谱密度，也常称其为能量谱，表示能量在某一频率上的分布集度：

式中，E 为能量信号s（t）的能量值，|s（f）|2为能量谱密度。

2.2.7 自相关函数

随机信号x（t）在不同的时刻具有一定相关性，自相关函数描述随机信号x（t）与t 的取值间相关度。函数中具有周期性分量，自相关函数能更好地反映这种周期性，其定义为随机信号在两个不同时刻乘机的期望。

2.3 PCA降维与SVM分类

本文共提取了α波数据的8 个特征，但并不是所有数据特征都对信号分类有着积极的作用，因此本文采用PCA 方法对特征数据进行降维，将8 维数据集降至3维，这样不仅大大降低了分类的复杂度，同时也提高了信号分类的可靠性。本文采用线性SVM 对特征数据进行二分类，利用降维后的3 组特征分类得到左向和右向两种脑电信号。首先利用降维之前的8 种特征进行分类，再利用降维之后的3 种特征进行分类，对比分类效果。

3 实验过程与结果分析

3.1 数据采集及预处理

受试对象是一名25 岁身体健康且无精神疾病的男性，听觉正常，测试环境温湿度正常，安静无明显杂音。本次测试采用听觉诱发方式，采集数据过程总时长15 s。0～5 s内，由录音机播放预先录制好的音频指令，指示受试者运动想象任务；5～10 s 为放松准备时间；10～13 s 进行脑电信号的采集，计算机自动存储数据；13 s 后采集的数据噪声较大，不予采用。实验过程如图1、图2 所示。

图1 右向实验过程

图2 左向实验过程

采集到原始数据后，由于脑电信号主要集中在0～200 Hz 的低频段且存在50 Hz 工频干扰，因此需要对原始数据进行低通滤波和50 Hz 陷波。本文设计了截止频率为250 Hz 的低通滤波器和50 Hz 的陷波器，保留了富含脑电信号的主要频段并初步滤除了工频干扰，以便后续进一步对脑电数据进行小波包分析。实验过程中采集了四导联脑电信号，通过反复测量信号幅度并比对不同区域脑信号的特点及频率范围，可以确定所测得的信号是真实的脑电信号，如图3 所示，图中各点是脑电信号采集过程中常用的采集点，其中A1和A2常用来做参考电极（耳夹电极），T3和T4位于太阳穴位置，信号强度较高，也可用于脑电采集。考虑到大脑C3区域的脑电信号对运动想象信号较为敏感，故采用C3区域采集的信号进行运动想象任务分析。

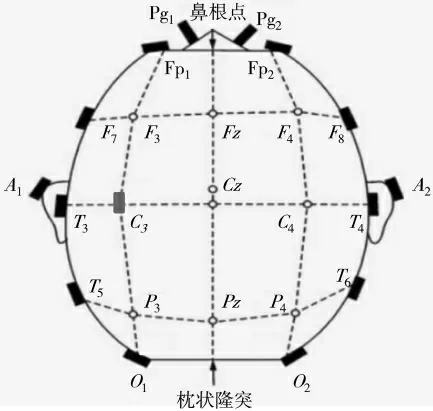
图3 电极位置示意图

图4 表示脑电4 个通道提取出的电信号，幅度采用归一化之后的幅度，这样可以方便进行比较，本文通过对C3通道的脑电信号进行数值分析，来实现运动想象分类任务。

图4 原始脑电波信号

3.2 算法过程及数据分析

对C3通道脑电进行7 层小波包分解，α 波处于8～13 Hz 频段[11]，故采用节点[7，5]、[7，6]和[7，7]对信号进行重构。小波包分解树状图如图5 所示,为简明表示，这里仅展示3 层小波包分解的树状图，重构得到的脑电α波左右手运动想象信号如图6 所示。

图5 树状分解

图6 α 波信号波形

对α 波信号进行频谱分析，发现其频率范围主要分布在8～13 Hz，如图7 所示。这证明了通过小波包方法提取的α 波是可靠的。

图7 α 波幅频特性

提取多个脑电α 波的数据特征[12]：均值、标准差、最大值、最小值、中位数、功率谱、能量谱、自相关函数共计8 个数据特征。为使各特征数据离相关，使用PCA 方法将8 维数据降维至3维，如图8、图9 所示，降维后的数据彼此相互正交，更具代表性。

图8 PCA 三特征运动想象分类

图9 相关特征波形

3.3 分类效果比较

如图10、图11 所示不同灰度分别表示左右手信号脑电α 波的特征点数据（上方数据点表示右手信号，下方则表示同一次实验中的左手信号）。对比可以发现降维之后的分类准确率明显上升。首先用降维之前的数据特征进行SVM 分类，然后利用SVM 方法对剩余的3 个特征进行线性分类[13]，分类结果投影到第一和第二个特征所在的平面，信号分类的准确度由90.1%提高至94.0%，如表1 所示。

图10 8 特征SVM 分类示意图

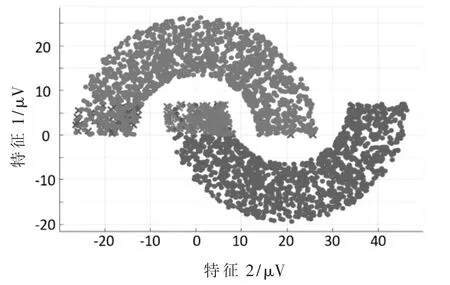
图11 3 特征SVM 分类示意图

表1 PCA 前后分类准确率对比

4 结论

为了提高基于脑电信号的运动想象分类准确率，本文将主成分分析方法用于脑电特征降维，并辅助以小波分析方法实现了运动想象脑电分类，实验结果证明本文提出的方法能明显提高分类准确率，有较高的可行性。

此外，本文采用支持向量机方法进行脑电运动想象数据二分类任务，而没有采用通常使用的BP 神经网络[14]，因为支持向量机方法更适用于二分类任务[15]，此方法在简单的脑电分类任务中也有着较强的参考价值。