初中数学规律性问题的分类研究

广西桂平市南木镇第一初级中学（537226） 李杰梅

笔者将规律性问题划分为数字变化类、算式变化类、坐标变化类、图形变化类四种类型。这四种类型问题涉及的背景不同，解题时需要学生在深刻理解题意的基础上进行合理的归纳和推理，尽快地找到隐含在题干中的规律。教学中，为了使学生更好地破解这四类问题，教师应为学生做好解题示范，使学生更好地掌握解题的技巧。

一、数字变化类

学生对数字变化类问题并不陌生，该类问题通常给出一组按照某一规律排列的数字，要求学生求出某一项数字的具体值。解答该类问题时需要从给出的已知条件出发，找到其潜在规律。如果题目中给出的数字是具体的，应认真观察数字，认真分析数字对应位数、前后项的变化情况，找到变化的值与对应序数之间的关系。如果题目中给出的数字是按照某一式子变化的，则需要运用归纳法进行分析。解题时一般写出数字的前面几项，相关的规律便会显现出来。学生若能掌握解题方法与技巧，积累解题经验，就能在解题中少走弯路。教师应做好经典例题的筛选与讲解，通过解题过程的板书，引导学生认真揣摩与反思解题过程，把握解题的关键。

［例1］已知在一列数x1，x2，x3，…中，x1=1，当k≥2 时（取整符号[a]表示不超过a的最大整数），则x2014的值为（ ）。

A.1 B.2 C.3 D.4

解析：该题的已知条件并不复杂，解题的关键在于从给出的等式关系中找到潜在规律。观察要求解的问题可知，其项数较大，一定存在周期。对此，可结合给出的等式关系以及对[a]含义的理解，算出前面的几个数，归纳出周期。

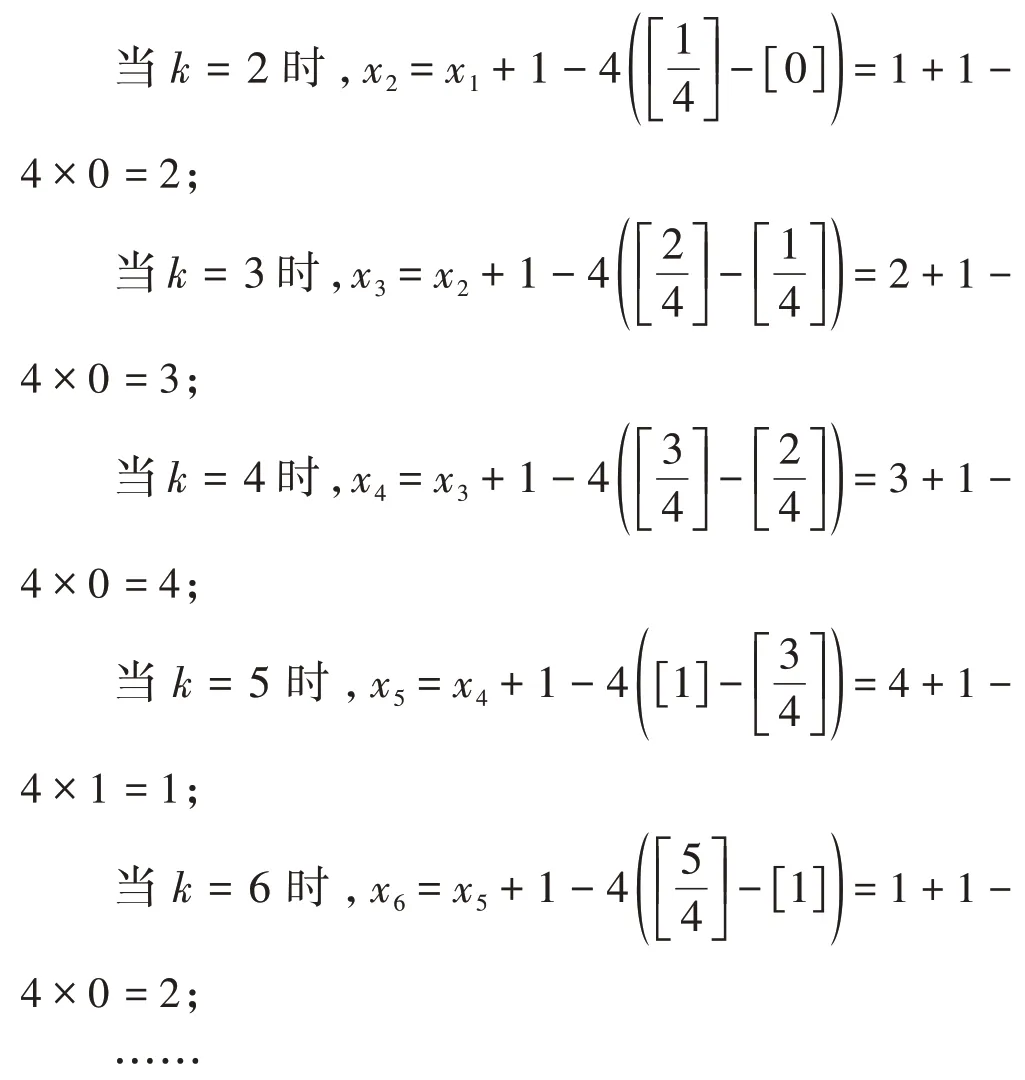
可知其每隔4 个数循环一次，其周期为4，则2014=503×4+2，∴x2014=x2=2，故选B。

点评：解答数字变化类问题时应注重分析题干，凡是要求解项数较大的具体数字时均具有一定的周期性，因此应将解题的重点放在归纳、推理其周期上。

二、算式变化类

算式变化类问题一般指运算法则按照一定规则变化的问题。解答该类问题的常规思路：审题，吃透题意→按照运算法则计算出结果→分析结果，寻找规律。其中“分析结果，寻找规律”对学生的观察、分析能力要求较高。对此，教师应引导学生牢记常规解法，认真审题，按照给出的运算法则认真计算，并通过观察结果的形式、各数字所处的位置，分析数字的变化规律，写出符合所有结果的通式。

［例2］某计算机程序如图1 所示，每次运算均是将一个数先乘以2，再除以它与1的和，多次重复进行这种运算的过程如下：

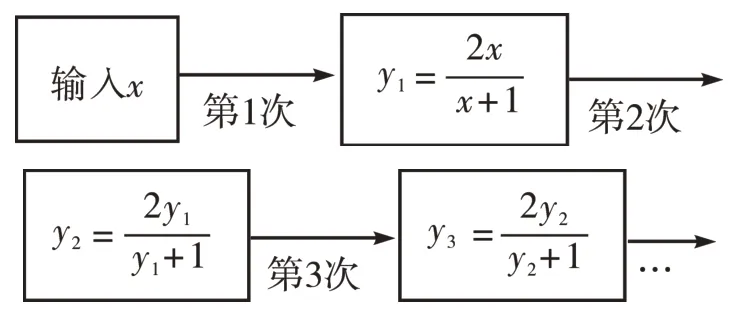
图1

若将π输入进去，则y10的值为（ ）。

解析：要想求出y10的具体值还应根据给出的程序分别写出y1，y2，y3，y4，认真观察结果的构成，看能否找到所得结果的规律。

点评：该题计算较为复杂，但是只要找到正确的解题方向和规律，便不难解答。需要注意的是，得出计算结果后应注重化简，分析分子、分母和计算次数之间的关系。

三、坐标变化类

坐标变化类问题通常和函数图像结合在一起，解答该类问题，需要学生在明确求解问题的基础上，运用函数、几何图形的性质分析坐标间的关系，以及应用函数图像的平移规律、规则图形的相关性质、三角形全等、三角形相似的判定等。不仅如此，还需要结合具体的情境作出辅助线，以更好地计算相关坐标。

［例3］如图2，△OA1B1，△A1A2B2，△A2A3B3…是以B1，B2，B3…为直角顶点，斜边在x轴正半轴上的等腰直角三角形，直角顶点B（1x1,y1），B2（x2,y2），B3（x3,y3），…均在反比例函数(x＞0)的图像上，则y1+y2+…+y10的值为（ ）。

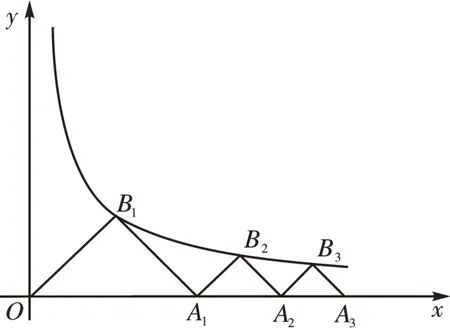
图2

解析：该题是等腰直角三角形和反比例函数相结合的综合性问题，较为抽象，而且已知条件中未直接给出对应点的坐标。可设计如下问题引导学生思考：（1）怎样求直角顶点的坐标？（2）等腰直角三角形有什么性质？（3）相加计算时应注意哪些细节？

显然，需要作出对应的辅助线。等腰直角三角形斜边上的高等于斜边的一半，运用给出的反比例函数，可分别求出y1，y2，y3，…，y10，而后进行相加运算。为降低运算的复杂度，求和时应注重相关规律的应用。

如图3，分别由B1，B2，B3，…向x轴正半轴作垂线，垂足分别为D1，D2，D3，…对于△OA1B1，因其为等腰直角三角形，容易得出OD1=D1B1，因为B1在反比例函数的图像上，所以B1的坐标为（2,2）。设A1D2=a，则B2（4+a,a），代入0)，解得即；同理，y3=所以故选A。

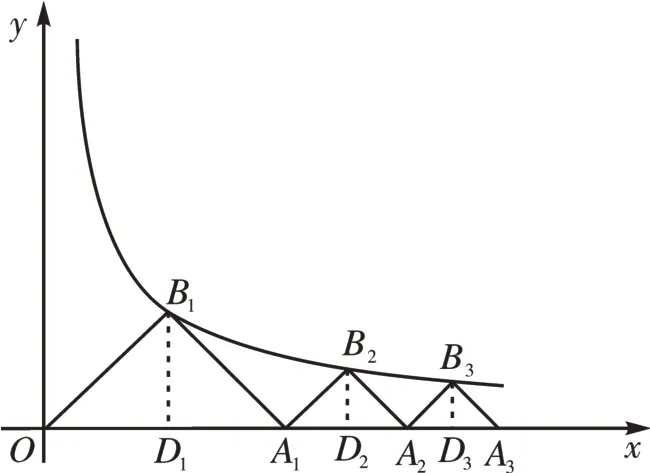
图3

点评：解答坐标变化类问题时应具备灵活的思维，注重几何知识的灵活应用，同时在计算时应注意观察，掌握相关的计算规律。

四、图形变化类

图形变化类问题要求学生根据图形的变化求解图形的角度、图形的线段长度、周长以及面积等。突破该类问题的关键在于找到图形变化前后的规律。该类问题创设的情境复杂多变，部分习题难度较大，因此教师应多给学生提供不同的情境，多与学生互动，避免其走进解题的误区。同时，注重运用多媒体技术为学生动态展示相关图形的变化，使学生能够清晰地看到图形变化过程中角度、线段长度等的变化，帮助其更好地找到解题的思路。

［例4］如图4，已知△ABC的面积为1，第一次操作：分别延长AB，BC，CA至A1，B1，C1，使得A1B=AB，B1C=BC，C1A=CA，顺次连接A1，B1，C1得到△A1B1C1；第二次操作延长A1B1，B1C1，C1A1至A2、B2、C2，使得A2B1=A1B1，B2C1=B1C1，C2A1=C1A1，顺次连接A2，B2，C2，得到△A2B2C2，按照此规律进行下去，若使得到的三角形的面积超过2019，则至少需要经过（ ）次操作。

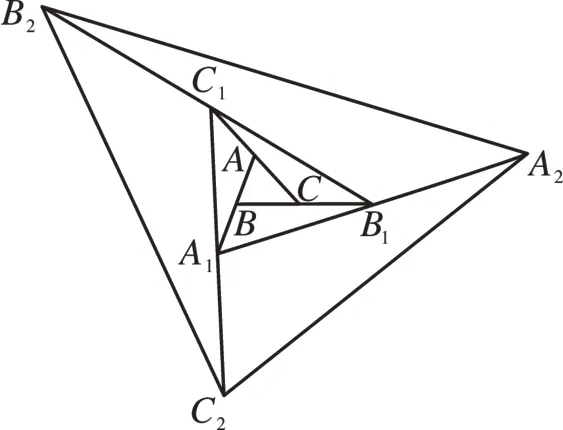
图4

A.4 B.5 C.6 D.7

解析：该题文字叙述较多，难度较大，只有充分理解题意，挖掘潜在的变化规律，才能顺利地求解。教师应引导学生作出相关的图形，并通过认真地对比、分析，挖掘题干中的隐含信息，找到操作后得到的三角形与原三角形面积之间的关系。

连接BC1，则其为△A1AC1的中线，则S△ABC=S△BAC1=S△A1AC1=1，则第一次操作后得到的三角形面积为2×3+1=7。同理，第二次操作后，△A2B2C2的面积为△A1B1C1的7 倍，为7×7=49，以此类推，第三次、第四次操作后得到的三角形的面积分别为49×7=343、343×7=2401，若要想满足题意则至少需要进行4次操作，故选A。

点评：解答图形变化类问题时应注重把握变与不变的量，分析变量是怎样变化的，而后进行有规律的计算。

为了提高学生解答规律性问题的能力，教师应结合学生的实际情况，制订明确的教学目标与教学计划，既要注重相关解题技巧的教学，又要对习题分门别类地整理，优选精讲经典例题，更好地拓展学生视野，使其掌握解题规律。同时，及时组织学生的开展专题训练活动，趁热打铁，使学生将学到的知识内化为解题能力，灵活地解答各类问题。