基于热平衡模型的镍铁电炉功率在线优化控制
2022-07-22徐小锋
李 刚,徐小锋
(中国恩菲工程技术有限公司,北京 100083)
0 引言
回转窑-电炉工艺(以下称RKEF 工艺)是目前火法冶炼镍铁合金的主流工艺,由于其具有产品品位高、熔炼电炉可控性强、生产效率高、易于实现生产扩大化等优点[1-2],在实际工程中获得了广泛的应用。近年来由于不锈钢、新能源汽车动力电池等行业对金属镍的需求旺盛[3],促进了了众多新兴RKEF 镍铁工程。
RKEF 主工艺流程包括干燥窑干燥、配料、回转窑预还原焙烧、电炉还原熔炼、镍铁精炼等[4],其中电炉还原熔炼是整个流程的核心。在能耗上,电炉消耗的电能占整个冶炼厂电能消耗的80%以上,电费成本占到整个产品成本的30%左右[5-6];在工艺上,电炉的运行最为复杂,其操作和控制水平对最终工艺指标和生产效益有着决定性的影响[7]。
镍铁电炉通常采用埋弧或遮弧运行方式,其原理是通过电极对渣层施加电压并借助电弧及渣电阻产生热能,使进入炉内的焙砂不断熔化、反应并分离出镍铁合金。在电炉操作中,对电极功率的控制至关重要,其决定了整个系统的热量平衡:电极功率不足会导致渣温过低,使得渣黏度变大,影响镍还原和分离效果并造成排渣困难;电极功率过高则会导致渣温过高,降低炉衬寿命并导致能耗升高[8]。目前,电炉功率设定大都由操作人员根据经验和现场运行情况人为确定,可满足基本的生产要求,但由于电炉生产过程中干扰因素较多,比如进料量波动、焙砂温度变化、烟气波动等,受人的经验和操作等问题影响,传统方式难以保证功率给定的实时最优性,从而对产品指标、产量和能耗等产生影响。
对于电炉的功率调节和控制目前已有众多的研究成果[9-12],但解决的是底层控制问题,即如何有效地控制功率在人为给出的设定值,而对于如何在线确定电炉的最优设定功率,实现上层优化控制鲜有文献涉及。
本文提出一种镍铁电炉功率在线优化方法,通过建立电炉的热平衡模型,并利用对电炉进料、烟气和冷却系统相关过程变量的实时检测,实现电炉功率最优设定值的在线计算。为减小热平衡计算误差和提高可靠性和适应性,构建了神经网络误差模型并用于热平衡计算的在线修正。最后采用数据仿真试验验证方法的有效性。
1 电炉功率在线优化
1.1 热平衡模型
镍铁熔炼电炉热量收支情况如图1所示[13],其中热收入项包括电能发热Qi1,进料焙砂显热Qi2及化学反应热Qi3;热支出项包括炉体损失热量Qo1,烟气损失热量Qo2,炉渣显热Qo3及镍铁水显热Qo4。

图1 镍铁电炉热量收支情况示意Fig.1 Schematic diagram of heat input and output of ferronickel electric furnace

由式(1)可知,通过确定其他6 项热量收支项(Qi2,Qi3,Qo1,Qo2,Qo3,Qo4),即可得到电炉所需的电能发热Qi1,进而得出所需的电加热功率。
1.2 热量收支项在线计算
各热量收支项的在线测量和计算方法如下所述,各式中热量单位为J,温度单位为K,时间单位为s,重量单位为kg,体积单位为m3。
1.2.1 进料焙砂显热Qi2
通过在线测量焙砂温度TC(t)和焙砂进料量WC(t),可由式(2)计算出Qi2。

式中:QC(t)为每千克焙砂在温度TC(t)下携带的显热,J/kg,其值可通过对焙砂中各成分的比热熔从298 K 至温度TC(t)进行积分,并根据各成分所占的质量分数进行折算后求和得出;Δt为优化控制周期;t0为周期的起始时间。以下同字符参数意义相同。
1.2.2 化学反应热Qi3Qi3可通过式(3)计算得出。

式中:热焓H298,Δ为每千克焙砂对应的化学反应热,J/kg,其值可通过参与反应的各产出化合物的标准生成焓减去各投入化合物的标准生成焓,并根据化合物的摩尔质量折算得出。
1.2.3 炉体损失热量Qo1
Qo1主要由炉墙、炉盖和炉底热量损失构成。其中炉墙部分热量损失可通过在线测量炉体冷却水进出口温度(得到温度差ΔTW(t))和冷却水流量FW(t)经计算得到,炉盖、炉底及其他未知热量损失由经验数据确定(设其总和为Qo1_Others),最终炉体的总热量损失计算见式(4)。

式中:CW为冷却水的比热容,J/kg·K;ρW为冷却水的密度,kg/m3。
1.2.4 烟气损失热量Qo2
Qo2可通过在线测量烟气温度TG(t)和烟气流量FG(t),经式(5)计算得出。

式中:ρG为烟气密度,kg/m3;QG为每千克烟气在温度TG(t)下携带的显热,J/kg;其值可通过对烟气中各成分的比热熔从298 K 升至温度TG(t)进行积分,并根据各成分所占的质量分数进行折算后求和得出。
1.2.5 炉渣显热Qo3
Qo3可通过式(6)计算得出。

式中:WS(t)为每秒产出的炉渣量,kg/s;由焙砂进料量WC(t)经物料衡算得出;QS(t)为每千克炉渣在温度TS_SET(设定的理想炉渣温度)下携带的显热,J/kg;其值可通过对炉渣中各成分的比热熔从298 K升至温度TS_SET进行积分,并根据各成分所占的质量分数进行折算后求和得出;ΔHSP(t)为每千克炉渣对应的相变热,J/kg;其值由炉渣各成分及其所占的质量分数决定。
1.2.6 镍铁水显热Qo4
Qo4可通过式(7)计算得出。
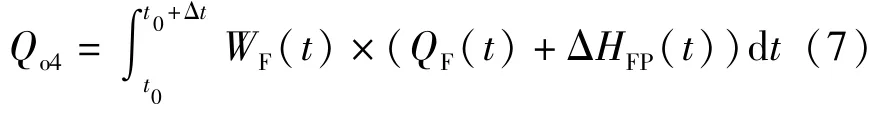
式中:WF(t)为每秒产出的镍铁量,kg/s,由焙砂进料量WC(t)经物料平衡计算得出;QF(t)为每千克镍铁水在温度TF_SET(设定的理想镍铁水温度)下携带的显热,J/kg;其值可通过对镍铁水中各成分的比热熔从298 K 升至温度TF_SET进行积分,并根据各成分所占的质量分数进行折算后求和得出;ΔHSP(t)为每千克镍铁水对应的相变热,其值由镍铁水各成分及其所占的质量分数决定,J/kg。
1.3 优化控制周期的选取
控制周期Δt的选取需综合考虑镍铁电炉的热量波动频度以及电极调节系统硬件限制等因素。Δt过大,无法对进料及烟气等扰动作出及时的响应,导致功率给定不能适应不断变化的热平衡需求,控制效果变差;Δt取值过小,则会导致电极调节系统因频繁动作而影响寿命。根据现场运行情况,Δt的经验取值范围为300~600 s。
1.4 电功率计算
由前述各热量收支项计算所需电能发热量,并由J 折算为kW 得到电炉功率的最优设定值PSET,具体计算见式(8)。

2 误差修正
理论热平衡计算与实际过程不可避免存在一定程度的偏差,过程量的测量等环节也可能产生误差,为保证控制效果需对总的误差加以修正。由于误差的形成原因复杂且不确定,难以采用解析的分析方法,因此采用BP 神经网络方法对其进行建模和预测[15-16]。
2.1 神经网络误差模型
选取进料焙砂显热Qi2、炉体损失热量Qo1和烟气损失热量Qo2作为输入层变量,热平衡热量偏差QΔ作为输出层变量,选用sigmoid 函数作为隐含层函数,构建如图2所示的3 层(3-4-1)BP 神经网络模型。

图2 神经网络结构Fig.2 Neural network model
2.2 神经网络训练
利用实测过程数据生成数据样本,并用于神经网络误差模型的迭代训练,具体步骤如下所述。
2.2.1 模型输出数据(QΔ)生成
热平衡模型的热量计算偏差可通过实际渣温的偏差计算得出,设排渣时测得的实际渣温为TS_Real,理想渣温设定值为TS_SET,则热量偏差QΔ可由式(9)计算得出。

式中:QS(TS_Real)为实际渣温对应的炉渣潜热,QS(TS_SET)为理想渣温对应的炉渣潜热,二者可利用式(6)进行计算求得。由于实际生产中,渣温只能在排渣时通过离线测量得到,故将1 个排渣周期tSP(相邻2 次排渣结束点之间时间间隔)作为热量计算和数据样本采集的周期。
2.2.2 模型输入数据(Qi2,Qo1,Qo2)生成
对应步骤2.2.1 中的排渣周期,分别借助公式(2)(4)(5)得到该周期内的进料焙砂显热Qi2,炉体损失热量Qo1和烟气损失热量Qo2。
2.2.3 数据预处理
将各排渣批次i生成的数据(QΔ)i和(Qi2,Qo1,Qo2)i进行归一化处理,使其值分布在[0,1]区间,以适应神经网络的取值要求,得到最终样本集合[(Qi2,Qo1,Qo2,QΔ)′i=1~n]。
2.2.4 网络训练和更新
将归一化处理后的数据样本集合用于神经网络进行迭代训练,经误差收敛后即得到神经网络误差模型。为适应生产过程的不断变化,可定期更新数据样本并重复以上训练步骤,实现误差模型的更新。
2.3 误差在线修正
利用神经网络误差模型对热平衡计算误差进行在线修正。在各优化控制周期内,将热平衡计算得到的(Qi2,Qo1,Qo2)代入神经网络误差模型的输入,将模型输出的QΔ用于热量修正,修正后的功率计算公式见式(10)。

3 电炉在线优化控制
镍铁电炉功率的在线优化控制步骤如下所述。
1)对进料焙砂成分进行检测分析,确定物料成分并进行物料平衡计算。
2)根据物料平衡计算结果,确定热量计算公式(2)~(7)中的相关系数。
3)设定优化控制计算周期Δt,与DCS 控制系统通信获得焙砂温度TC、进料量WC、炉体冷却水进出口温度差ΔTW及流量FW、烟气温度TG及流量FG的实时测量值。
4)利用公式(2)~(7)计算各项热量收支值:Qi2,Qi3,Qo1,Qo2,Qo3,Qo4;利用神经网络误差模型计算热量修正值QΔ;利用公式(10)计算最优功率值并发送至DCS系统作为功率设定。
5)在电炉排渣周期测量实际出渣温度TS_Real,根据2.2 节中的步骤生成数据样本并用于神经网络模型的定期训练更新。
镍铁电炉在线优化控制系统流程如图3所示。

图3 镍铁电炉在线优化控制系统流程Fig.3 Online optimization control system process for nickel-iron electric furnace
4 数据仿真验证试验
某RKEF 镍铁冶炼工程,电炉额定设计功率为55 MW,电炉渣温和铁水温度的设定值分别为1 580 ℃、1 480 ℃,排渣周期平均在6 h 左右。对30个排渣批次的样本数据进行考察,其中15 组数据用于热平衡计算和仿真,剩余15 组数据用于神经网络误差模型的训练。
假定炉渣温度设定值为1 580 ℃,根据各组样本数据得到各排渣批次的分项热量计算结果如图4所示。图中,热收入项计为正值,热支出项计为负值。
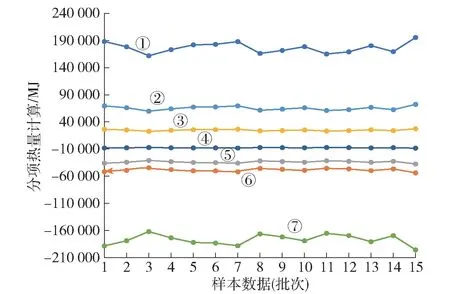
图4 热平衡计算Fig.4 Heat balance calculation
将实测渣温与其设定值相比较并折算为热量偏差,结果如图5中实线所示,其中最大批次热量偏差值为58 000 MJ,约占炉渣潜热的5%。采用第2 节中给出方法构建神经网络误差模型,并利用样本数据进行迭代训练。由训练好的神经网络误差模型对热量偏差进行预测,结果如图5中虚线所示。误差模型修正后,最大批次热量误差减小到6 000 MJ,占炉渣潜热的不到1%。上述仿真试验结果表明,采用热平衡模型及神经网络误差模型可实现准确的热量计算,进而实现有效的电炉功率优化控制。

图5 热量偏差及预测Fig.5 Heat calculation deviation and prediction
5 结语
本文建立了镍铁电炉的在线热平衡模型,通过在线测量相关过程变量并经热平衡计算得到所需电能发热功率,实现了电炉的最优功率设定;并通过构建神经网络误差模型实现了对热平衡模型误差的实时修正,提高了方法的准确性和适应性。
镍铁电炉功率在线优化控制系统解决了人工设定功率不准确、不及时的问题,实现了输入电能与冶炼需求的精确匹配,使渣温能够得到有效的控制,保证了镍回收率、生产效率、产品单耗等指标的最优性,解决了镍铁电炉智能冶炼的核心问题。该系统下一步研究重点是与其他子系统相结合,形成从原料分析到配料优化、在线优化控制、炉体监控、智能诊断等环节的完整智能冶炼厂解决方案[17]。
