纳米精度位移机构柔性铰链结构设计分析

曾 超 毛成文 何 燕 李爱国1,

1（中国科学院上海应用物理研究所 上海 201800）

2（中国科学院大学 北京 100049）

3（上海光源科学中心/中国科学院上海高等研究院 上海 201204）

上海光源硬X 射线纳米探针光束线（Hard Xray Nanoprobe beamline，HXN）目标瞄准约10 nm的聚焦光斑尺寸［1］，从而满足生物、材料和环境等多个前沿科学领域的实验要求。该光束线采用了多层膜Kirkpatrick-Baez（K-B）镜的纳米聚焦元件，其姿态精度对聚焦结果有着重要影响，需要对两个镜子的姿态进行高精度调整。这类K-B镜聚焦纳米系统对调节机构提出了一系列要求：具备nm级的运行定位精度和高稳定性；具有合适的运动行程，其有效运动行程为0.1~0.2 mm；满足结构强度、一定载荷、抗干扰等方面要求的同时，实现结构的轻量化和易驱动。

在众多微位移技术中，柔性铰链机构具有无机械摩擦、无间隙、运动灵敏度高的优点，被广泛应用于包括同步辐射光束线在内的诸多精密机械、微纳米器件的研制中［2-4］。针对不同的应用场景，目前已经发展了各种不同形状和不同转动方式的铰链形式［5-12］。在众多类型的柔性铰链中，标准的直圆型柔性铰链是一个理想的转动结构（如图1），其缺口部分为圆弧形，具有与几何中心轴重合的回转中心，在外力驱动下，绕其回转中心在有限范围内产生回转运动。相较于其他常用如倒角、椭圆型柔性铰链等，Xu 和King 等［13］通过有限元法分析比较得出，倒角型柔性铰链的变形量最大，而直圆型柔性铰链的运动精度最高，且结构简单易于加工，特别适用于小行程范围内纳米精度的运动。

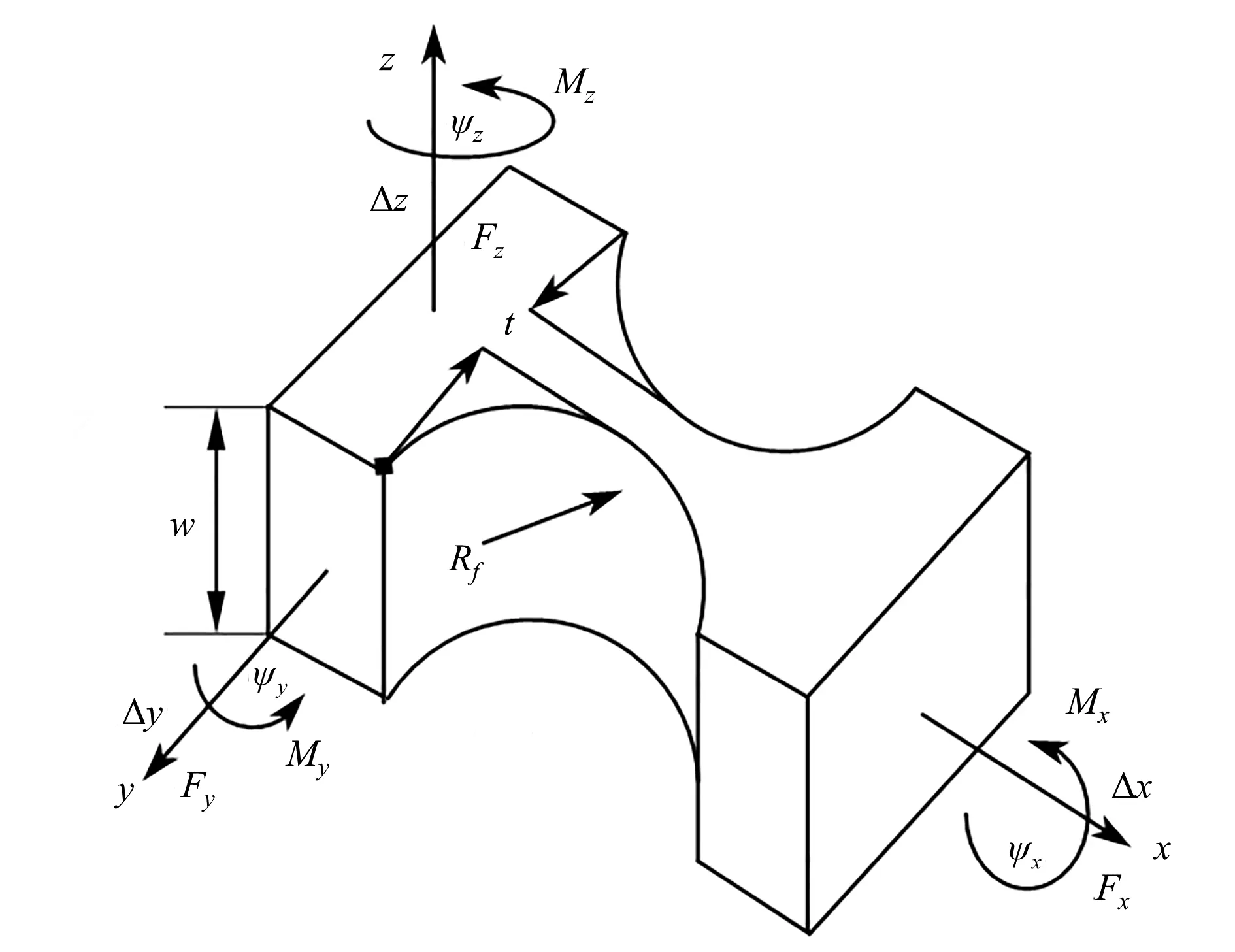
图1 直圆型柔性铰链示意图Fig.1 Diagram of circular flexure hinge

美国阿贡国家实验室APS 光源（Advanced Photon Source）已经开发了多种Weak-Link 柔性铰链机构［2-3］，该柔性铰链是基于光刻技术的光化学加工工艺制作［14］，通过刻蚀加工柔性铰链薄片，最后多片粘合堆叠成型。这种加工工艺可以确保柔性铰链在运动方向的柔性、非运动方向的刚性和高稳定性。如APS 基于直圆型柔性铰链构型，应用在人工切槽晶体单色器［2］和硬X射线偏振器［15］中的柔性铰链机构，在角度调节上分别可达20~40 nrad 和80 nrad 的角分辨率；在位移调节上，包括APS T8-31/T8-32 以及T8-41/T8-42 等位移台［16-17］，在水平和垂直方向上均可达到10 nm的闭环分辨率，而T8-37/38位移台［2］的闭环分辨率可达1 nm。在上海光源硬X 射线微聚焦及应用线站BL15U1，前期与美国APS 合作研制出高精度柔性铰链压弯机构，使用该压弯镜在国内实现了＜350 nm的硬X射线聚焦光斑［18］。鉴于目前的国际环境，已经无法继续使用该工艺技术。欧洲ESRF 光 源（European Synchrotron Radiation Facility）则使用传统的慢走丝线切割工艺整体加工的四连杆直圆柔性铰链压弯机构，已经实现了＜50 nm 的聚焦光斑［19］。但慢走丝线切割在加工多孔结构的柔性铰链时，对穿丝和校准等工艺有非常高的要求，目前国内缺乏相应的经验积累。而近年来，一体加工和轻量化的增材制造技术发展迅速，随着金属领域的3D 打印工艺日趋完善，通过3D 打印的方式发展柔性铰链机构是一种可行的技术路线。

为了满足类似上海光源HXN 线站纳米聚焦的高精度高稳定性需求，本文研究了一种基于直圆型结构的平行线性柔性铰链机构，通过弹性力学对该机构开展结构分析和有限元方法对比验证，采用3D打印方式制造了该铰链机构，并初步验证了该机构的稳定性和可用性。

1 用于高精度平移运动机构的柔性铰链设计分析

平行连杆是一种成熟的机构，可以有效地在平行方向上传递运动。图2是由数对直圆柔性铰链组成的平行多连杆柔性铰链机构。其主要特征为每两个直圆型柔性铰链与一个刚性杆连接，每对柔性铰链与顶部的刚性导向杆连接。平移时每个柔性铰链的转动线互相平行并且垂直于导向杆，所有结构均在同一平面内。为了满足不同工作场景（如行程、负载、装配）的需求，该平行连杆机构中柔性铰链的尺寸、数量等参数可以适当调节。基于该结构设计的铰链机构，期望能够在满足设计行程的同时，具有高精度和高刚性的优点。此外，其结构紧凑的特点也便于与其他机械装置结合。

图2 平行连杆柔性铰链机构示意图(a)四铰链，(b)八铰链Fig.2 Diagram of parallel linkage flexure hinge mechanism(a)Four-hinges,(b)Eight-hinges

1.1 弹性力学解析

对于图2的柔性铰链，无论铰链数量是多少，每个柔性铰链机构的上部相当于刚体，仅起导向作用，下部起固定约束作用。在力F的作用下，每组柔性铰链会产生相同的变形，每组铰链的受力也相同。假设采用的铰链对数为n（即铰链数量为2n），则每对柔性铰链受到的力为F/n，所以在分析时可以只选取一组柔性铰链。同时考虑到每组铰链的上下对称性，再取一半进行分析，分析示意图如图3所示。其中：Rf为铰链的切割半径；t为最小厚度；w为铰链的整体厚度；E为材料的弹性模量；L为连接杆的长度。

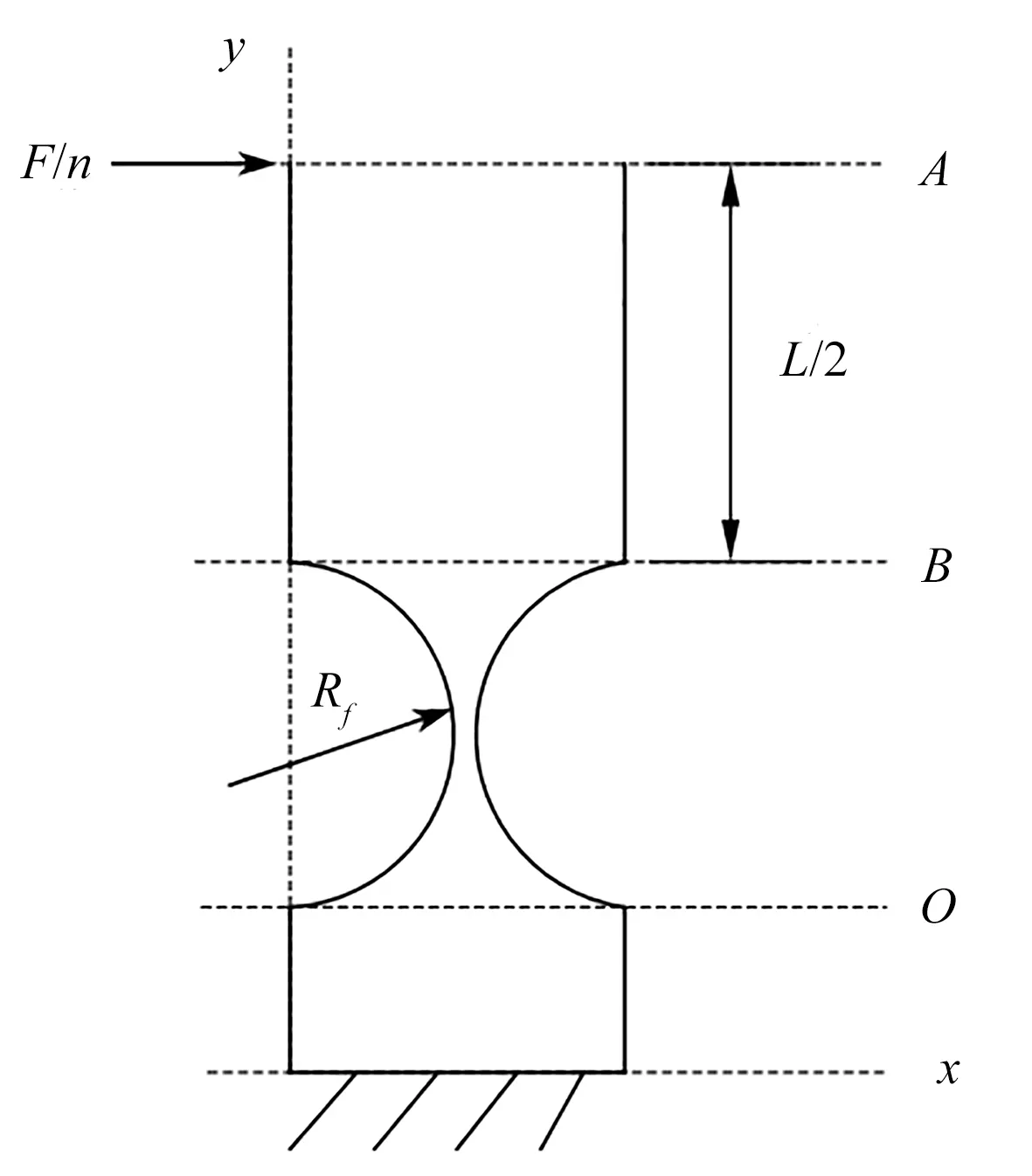
图3 柔性铰链分析示意图Fig.3 Analysis schematic of flexure hinge

从图3可知，在力的作用下，截面A会往力的方向产生位移，其位移量由AB段和OB段截面共同产生。故分别计算它们所产生的位移，最后进行叠加，可以计算出在力的作用下柔性铰链的运动位移。

对于其中的AB段，这一段相当于一端固定，一端自由的悬臂梁，故可以直接由材料力学公式［20］计算得出：

图3中的OB段为直圆柔性铰链的变形部分。对于该部分的求解，Paros 和Weisboro 在1965 年便基于弹性力学基本公式和微积分理论巧妙地推导出了单个柔性铰链的设计公式［21］，得到了不同方向上转动和平移刚度的精确解。但由于其给出的精确计算公式在形式上仍较为复杂，吴鹰飞等［22-23］在其基础上简化了其计算公式，在力F0的作用下，单个直圆型柔性铰链沿x轴的线性变形Δx，其计算表达式如下：

式中：s=Rf t。由于在实际中，铰链的最大运动范围还与材料的屈服应力σs密切相关，在t≪2Rf的条件下，可以得到柔性铰链的最大转角与材料屈服应力之间的近似计算式：

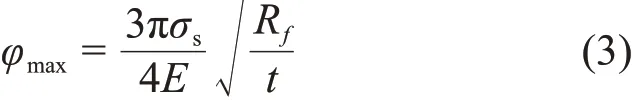
由以上计算式可知，在推力的作用下，柔性铰链沿力方向上的位移由计算式（2）得出，故将F0=F n代入（2）式即得由OB段引起的截面B的位移为x2。

因此截面A的位移为x1+x2，通过式（1）、（2）计算即可得到该柔性铰链机构的总位移为：

根据实际应用需求，柔性铰链采用17—7PH 不锈钢材料，其弹性模量为E=203.4 GPa，柔性铰链的特征参数为：最小厚度t=0.15 mm，切割半径Rf=1.62 mm，连接杆长度L=6.33 mm，厚度w=1.52 mm，力F为3 N。将上述参数代入式（4）计算，结果如表1 所示。从表1 可知，随着铰链对数的增加，在驱动力不变的条件下，其输出位移越小，刚性越强。

表1 弹性力学解析下不同铰链数量的输出位移结果Table 1 Displacement results of theory of elasticity under different number of hinge

1.2 有限元仿真验证

为了验证柔性铰链的解析计算结果，采用有限元方法建立模型并进行静力学分析。柔性铰链的缺口处是整体最薄弱的部分，这个部分需要划分较密的网格，其余部分可以划分较稀疏的网格以节约计算资源。

根据理论计算得到的结果，选用3 N 外力作用下行程较为合适的n=4与n=6两种情况作有限元分析。材料选用17-7PH 不锈钢材料，弹性模量为E=203.4 GPa，泊松比μ=0.3，密度ρ=7 780 kg·m-3，屈服强度为1 205 MPa。铰链底部采用固定约束，对铰链的一端施加3 N 的载荷，铰链最小厚度t=0.15 mm，将该部分网格控制在0.07 mm以下来保证该部分有两个以上网格。使用SolidWorks Simulation 静应力分析模块，计算得到铰链的输出位移分布如图4。

图4 柔性铰链输出位移分布示意图 (a)n=4，(b)n=6Fig.4 Displacement diagram of flexure hinge for FEA(a)n=4,(b)n=6

由有限元计算结果可知，在3 N载荷的条件下，4对铰链结构产生的位移为0.213 5 mm，6对铰链结构产生的位移为0.142 2 mm。传统力学分析得到的计算结果分别为0.209 0 mm 和0.139 3 mm，两者误差均在2%左右。可以看出近似条件下的理论计算与有限元分析的结果偏差较小。

上述最低能耗的轨迹研究，都是在轨迹周期T=0.35的条件下进行的实验，但在工业现场因工作环境不同，要求的拾放操作周期也不同，因此了解不同轨迹在不同周期的最低能耗情况，对工业现场的操作更具意义。为计算不同时间周期轨迹的最低能耗轨迹，可以重复4.1节的步骤，进行实验验证。以电机输入电能为验证指标，实验能耗趋势如图8所示；以机器人机械能耗为验证指标，实验能耗趋势如图9所示。

为了进一步验证计算，在采用步进力条件作用下，对n=6 时的铰链结构进行重复计算，结果如表2所示。

表2 17-7PH材料下理论计算与有限元分析结果Table 2 Results of theoretical calculation and FEA under material of 17-7PH

在表2 中，误差一栏是传统理论计算与有限元分析结果之间的误差。由表中结果可以看出，在恰当设置边界条件和网格良好划分的情况下，传统理论计算的结果与有限元的分析结果之间的偏差基本稳定，在不同驱动力条件下误差均约2%。

1.3 各关键参数对输出位移的影响

从对该平行连杆柔性铰链机构的分析可知，在一定外力作用下影响其输出位移的主要影响因素有：切割半径Rf、最小厚度t、铰链厚度w、连接杆长度L、材料弹性模量E、屈服应力σs等特征参数。由式（4）可以得到在n=6，F为3 N 条件下各参数对其输出位移的影响。如图5 所示，由图5 可以得知，输出位移随着切割半径和连接杆长度的增加而增加、随着铰链厚度和最小厚度的增大而减小，且在这些参数中，最小厚度t的变化对输出位移的影响最大。

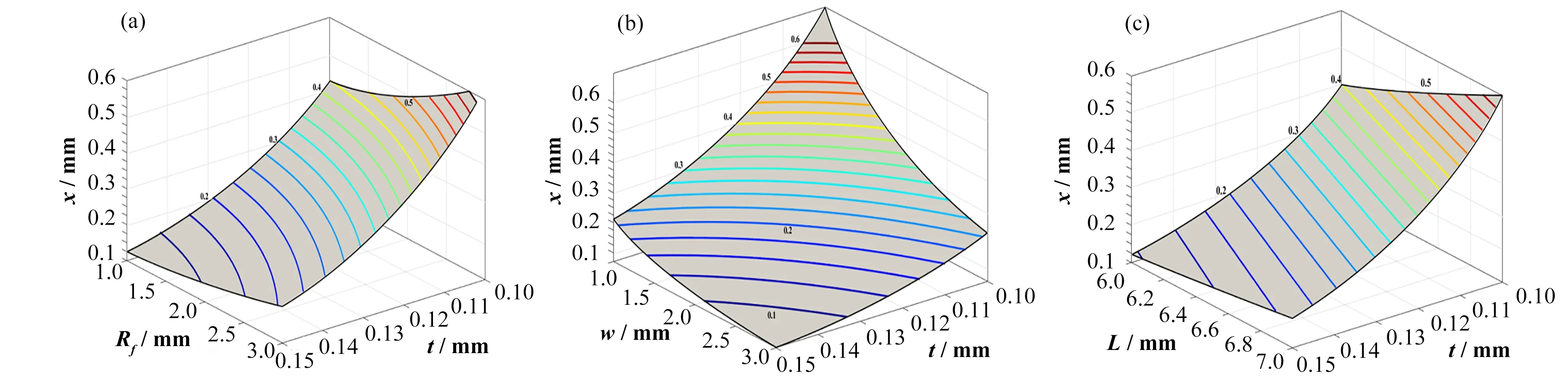
图5 切割半径、最小厚度(a)、铰链厚度、最小厚度(b)、连接杆长度、最小厚度(c)对输出位移的影响Fig.5 Effect of radius and minimum thickness on displacement(a),thickness of hinge and minimum thickness on displacement(b),length of connecting rod and minimum thickness on displacement(c)

对于铰链的数量n，其数目越多，越能够平均单铰链加工误差所带来的影响。此外通过对称、垂直等结构设计装配多片铰链还可以增强整体结构的强度：根据表1 计算结果，在n=6 时3 N 的驱动力提供了0.139 3 mm 的输出位移，而n=7 时则仅有0.119 4 mm。如采用德国PI 的公司的N-470 促动器，其轴向力为22 N，若采用四片n=6的铰链作为运动结构，并装配弹力为10 N 的恢复弹簧，则每片铰链在促动器推动时受力约为3 N，反向移动受到的弹簧弹力为2.5 N。因此若采用更大的n值，在实际工程中需要使用更大推力以及更大尺寸的促动器以保证足够的行程，在成本和空间上都带来了更高挑战。

除此之外，材料本身的特性对其输出特性也有较大影响。根据材料的许用应力定义［σ］=σs/λ，设定安全系数λ为1.5，并将17-7PH不锈钢材料的屈服应力1 205 MPa 代入即可得到材料的许用应力约为803.3 MPa。在保持n=6 条件下，结合式（3）和式（4），可以得到该柔性铰链的最小厚度t与结构位移（最大安全位移和恒定驱动力驱动位移）的关系，示意图如图6所示。其中最大载荷是铰链结构在材料的许用强度下能承受的最大载荷。t越大，结构刚性和抗干扰能力也大幅度增加，同时驱动力也成指数剧增；t越小，结构传动灵敏度和分辨精度也增加，与此同时结构刚性和稳定性急剧降低，尤其t小于0.11 mm时，不到3 N的驱动力就会过载导致结构产生不可逆的塑性形变。如不考虑驱动力限制，在达到0.2 mm运动距离时，t最大允许值可达0.321 mm。此时单片铰链需要配适高达31 N的驱动力，对现有促动器提出较大的挑战。

图6 柔性铰链位移与铰链最小厚度关系示意图（n=6）Fig.6 Relationship diagram between displacement and the minimum thickness of the flexure hinge(n=6)

在其它参数上，切割半径Rf的影响虽然较小，但其值越小，铰链的变形区域也越小，越容易产生应力集中的现象。因此切割半径的最终设计值应尽量选取较大值。而对于铰链整体厚度参数w，由式（3）和式（4）可知，其大小对铰链的最大转动性能没有影响，增加整体厚度可以提高结构的侧向强度和稳定性，与此同时需要等比例调增驱动力。连接杆长度L与输出位移近似成正比关系，但过长的连接杆会降低铰链结构的刚性。

2 柔性铰链机构的稳定性分析

假设铰链机构的载荷大小为m，工作时运动方向上承受冲击的加速度为a。使用SolidWorks Simulation 的静应力分析模块分别对n=4 和n=6 两种不同铰链数量的结构进行有限元分析。这两种结构分别在较低负载（250 g）、中等负载（500 g）、较大负载（1 000 g）的条件下，结构不被破坏所能承受的最大耐受加速度amax，如表3、4所示。

从表3和表4中的结果可知，在负载和驱动力一定的情况下，6对铰链在250 g正常负载下承受的最大冲击加速度为11.409 0 m·s-2，4 对铰链能承受的最大冲击加速度为7.592 9 m·s-2。较多的铰链对能承受更大的冲击加速度，结构也会更安全。与此同时，更多的铰链对需要更大的驱动力，对促动器也提出了更高的要求。因此在实际工程设计中，需要根据现实技术条件和设计要求，在两者之间综合考量进行必要的平衡。

表3 柔性铰链在不同负载下的有限元计算结果（n=4）Table 3 Results of theoretical calculation and FEA under material of 17-7PH(n=4)

表4 柔性铰链在不同负载下的有限元计算结果（n=6）Table 4 Results of theoretical calculation and FEA under material of 17-7PH(n=6)

当铰链机构受到的外界激励频率接近固有频率时，会产生共振现象从而影响机构的稳定性。在动力学分析中，结构响应往往取决频率相对较小的低阶振型。低阶振动时系统的能量比较集中，所以低阶振型对结构动力影响程度比高阶大。在SolidWorks软件中使用频率分析模块，对4对及6对铰链机构分别进行模态分析。频率分析采用的网格划分策略与前文保持一致，给铰链底部施加固定约束，分析得到的系统前四阶的共振频率如表5所示，前四阶振型有限元分析结果如图7所示。

表5 两种铰链数量的前四阶共振频率计算结果Table 5 Results of first four resonance frequency under two number of hinge

图7 两种铰链数量前四阶振型图 (a)第一阶，(b)第二阶，(c)第三阶，(d)第四阶Fig.7 The first four order vibration mode of two kinds of flexure hinges for FEA(a)First order,(b)Second order,(c)Third order,(d)Fourth order

从模态分析的结果可知，该柔性铰链机构在任意模态下都不可避免的发生扭曲或变形。其中一阶模态主要是在运动端产生扭曲变形，对运动精度影响最大。4 对铰链与6 对铰链机构的一阶共振频率分别为318.55 Hz和380.01 Hz，6对铰链结构的频率更高且变形量相对更小；第二、三和第四阶模态主要是铰链中间和边角的挤压变形，通过固有频率的大小可知，6 对铰链的频率均较高于4 对铰链，表现更为稳定。而在上海光源硬X 射线纳米探针实验站上，振源主要为100 Hz 以内的低频，低阶固有频率对系统的影响更大。综合以上分析结果，两种结构的一阶固有频率均高于100 Hz，能够有效降低环境振动的影响。相较而言，6 对铰链的结构所受的负面影响更小，其稳定性与承载性也更好。

3 实验测量

为了验证柔性铰链设计的有效性并自主发展出一条铰链加工技术路线，根据前文所设计的铰链参数，率先利用金属3D 打印技术加工了柔性铰链样件，并进行了一维位移运动样机的装配调试，实物图如图8所示。

图8 柔性铰链样件(a)，基于3D打印柔性铰链的一维位移运动样机(b)Fig.8 Flexure hinge sample(a)and one-dimensional linear motion prototype based on 3D-printed flexure hinge(b)

为了提高机构在侧向上的刚性，减小单个柔性铰链的加工与装配的误差，该机构在垂直和水平方向上各装配了一对合计4片柔性铰链。促动器采用德国PI 的N-470，其最小步长为20 nm，轴向推力为22 N。位移测量采用美国LION-HVC5S 电容式位移传感器，在100 Hz采样频率以内时最高测量精度可达0.08 nm（RMS）。对该机构样机进行空载开环测试，测试结果如图9所示。

样机进行250 nm 短行程测量时的步长约为（26.8±0.2）nm。测量结果如图9（a）所示，图9（b）为图9（a）中所圈区域放大图。从图9 中可知，每个台阶位移抖动的均方根误差约为±1.1 nm，表明该铰链机构的稳定性较好。200 μm 长行程测量结果图9（c）可知，该机构在0.2 mm 范围内具有良好的线性运动特性，符合有限元及理论分析的结果。若要实现更高精度的位移调节与控制，需要使用更高精度带有闭环控制的促动器。测试结果表明：本文设计的柔性铰链机构与预期相符，并首次验证了金属3D打印是加工柔性铰链的一种可行技术路线。

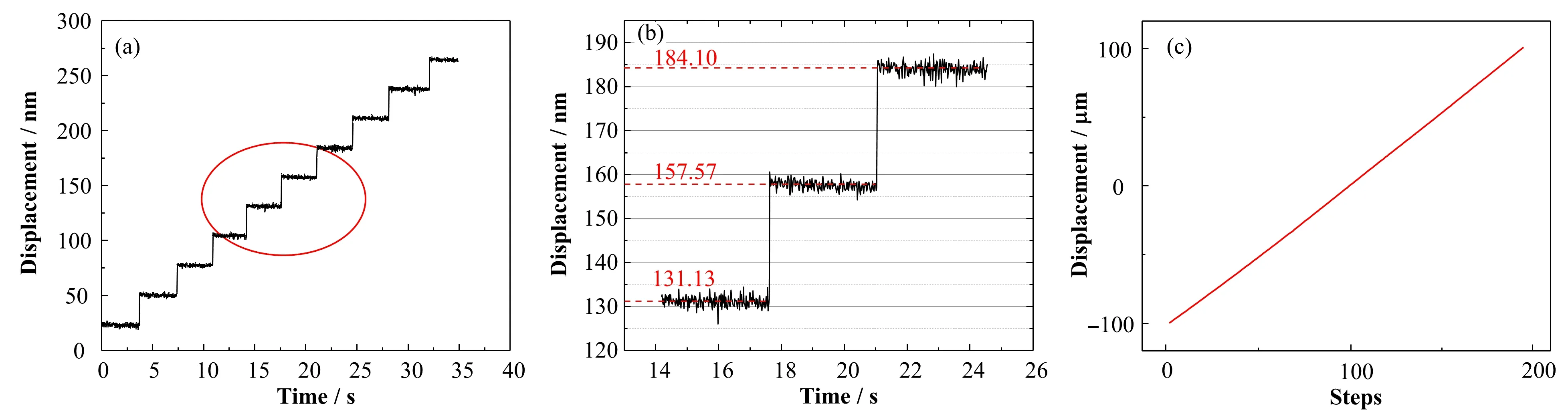
图9 样机测量结果 (a)250 nm短程测量，(b)短程测量局部数据，(c)200 μm长行程测量Fig.9 Measurement result of prototype (a)250 nm short-range measurement,(b)Short-range measurement of local data,(c)200 μm long-range measurement

4 结语

为满足同步辐射硬X射线K-B镜等纳米聚焦光学元件精密调节需求，采用了适合纳米运动的直圆柔性铰链为基础构型设计了用于一维线性运动的平行连杆柔性铰链机构。并分别采用了传统弹性力学分析和有限元计算方法对平行连杆柔性铰链结构进行了运动特性分析，结果表明理论计算和有限元的计算结果相符。在不同的驱动力条件下，理论分析与有限元计算结果误差约为2%。通过3D打印技术加工了柔性铰链和位移机构样机，测试结果表明该机构在采用两对n=6 的柔性铰链的情况下，实现了0.2 mm 运动行程，位置稳定性达到±1.1 nm（RMS），这将有助于在国内进一步自主研发适用于同步辐射的高精度高稳定调节机构。

作者贡献声明曾超：负责文献调研，实验测试，数据的整理与分析，文章的撰写；毛成文：负责模拟计算和指导实验测试；何燕：负责测试系统调试与数据的采集；李爱国：负责实验方案设计、文章指导和审阅。