JPEG图像被动取证研究进展综述
2022-07-22牛亚坤李晓龙
牛亚坤 赵 耀 李晓龙
(1.北京交通大学信息科学研究所,北京 100044;2.现代信息科学与网络技术北京市重点实验室,北京 100044)
1 引言
随着信息技术的迅速发展和数码产品的普及,以数字图像为代表的多媒体已经成为人们日常生活中重要的视觉信息载体,被广泛应用于新闻报道、司法鉴定、理赔保险和科学发现等领域。数字图像的广泛应用也促进了多媒体编辑软件的蓬勃发展,例如Photoshop、美图秀秀、美颜相机等。利用这些编辑工具,人们对数字图像内容修改变得简便快捷且能达到以假乱真的效果。然而,这些技术在给人们生活带来方便的同时也会造成一定的困扰和危害。一些具有不良目的的恶意用户会对图像内容进行非法操作,以达到制造虚假新闻、欺诈勒索、提供司法伪造证据等一系列违法犯罪活动的目的。可见,数字图像所传递的信息并不总是真实可靠、恶意伪造图像不仅扰乱治安稳定而且危害国家安全。因此,对数字图像内容真实性和完整性认证已经成为多媒体信息安全领域亟需解决的问题。在此背景下,数字图像被动取证技术应运而生,旨在利用图像的固有属性认证其原始性和真实性、对伪造区域定位以及分析操作历史[1]。该技术不需要预先对数字图像嵌入标识性信息,而是通过直接地分析图像内容本身,从而实现盲取证的目的,成为多媒体信息安全领域的热门研究方向。
JPEG作为通用的压缩标准,被广泛应用到数码相机和编辑软件。大多数社交平台,例如微信、Facebook 等也需要对上传的图像进行JPEG 压缩以便存储和传输。因此,对JPEG 图像进行取证具有现实意义。另外,对JPEG 图像进行篡改会留下特殊的压缩效应,分析这些效应能够更好的鉴定图像真实性以及定位篡改区域。本文旨在对现有JPEG图像相关的取证技术进行介绍、归纳和分析,以期为研究人员提供一份详尽的进展报告,推动相关领域的发展。
2 JPEG压缩编码和解码
标准的JPEG 压缩过程包括编码和解码阶段,如图1 所示。在编码阶段,一幅图像首先被分解为不重叠8 × 8 大小的块X1,然后对每个块进行离散余弦变换(Discrete Cosine Transform,DCT)得到DCT系数:
接着使用量化矩阵对DCT 系数进行量化得到量化系数[Y1/Q](也称JPEG 系数)。其中,[⋅]为四舍五入取整操作,Q为8 × 8 大小的量化矩阵,其包含64 个量化步长qi∈N,i∈{0,…63}。最后对量化系数进行熵编码。量化误差发生在编码阶段中,它是JPEG压缩信息损失的主要原因。在解码阶段,首先从码流中读取量化系数,然后对其反量化,得到
接着对Z1进行逆向的DCT 操作(Inverse DCT,IDCT),得到反变换系数:
由于数字图像像素的灰度级在[0,255]之内,需要对U1进行取整和截断,得到解压缩图像:
其中RT(⋅)为取整和截断操作。解码过程中会产生取整误差和截断误差。JPEG 图像中的各种误差、DCT 系数分布等均属于自身的“固有指纹”,任何的篡改方式都会在一定程度上破坏它们的统计特性并且留下特殊的痕迹,因此可以通过分析这些“固有指纹”的完整性和一致性对图像真实性进行鉴别。
3 JPEG图像被动取证方法
对JPEG 图像进行篡改时,拼接区域可能来自未压缩图像或另一幅JPEG 图像,完成拼接后篡改图像还需要第二次压缩。这样拼接图像中原始区域和拼接区域会出现压缩历史不一致性,即原始区域经历两次压缩,但拼接区域却经历一次压缩(拼接区域来自JPEG 图像时,压缩期间DCT 网格较大概率是非齐方式,也会呈现一次压缩现象)。另外,在隐蔽通信场景中,秘密信息被嵌入后,携密的JPEG 图像仍需进行第二次压缩进而出现双重压缩现象。因此,可以通过检测双重压缩进行篡改区域定位以及隐写分析。此外,分别从双重JPEG 压缩图像中估计初次量化矩阵和从解压缩图像中估计量化矩阵能够提供更加全面的信息用于进一步的取证分析。利用压缩次数、JPEG 压缩中的误差、DCT 系数直方图和量化矩阵等“固有指纹”不一致性还可以对拼接区域检测和定位。因此,JPEG图像取证可以划分为:双重JPEG 压缩检测、量化矩阵估计和JPEG图像拼接检测与定位。
3.1 双重JPEG压缩检测
根据两次JPEG 压缩使用的量化矩阵是否一致,压缩可以分为不同量化矩阵和相同量化矩阵的双重JPEG 压缩。对于不同量化矩阵的双重JPEG压缩检测,研究学者已经提出众多有效的方法,其可以被分为基于手工特征和基于卷积神经网络(Convolutional Neural Network,CNN)的方法。
对于基于手工特征的方法,Popescu 和Farid[2]首次发现双重压缩图像的量化系数直方图会出现周期性的峰值和峰谷现象,称为双量化(Double Quantization,DQ)效应。通过对量化系数直方图傅里叶变换测量周期性然后用于检测双重JPEG 压缩。但当第一次压缩的质量因子较大时,该方法将会失效。另外,当两次压缩之间存在裁剪操作时则不存在DQ 效应。Fu 等人[3]观测到单次压缩图像的交流(Alternating Current,AC)系数首数字的分布遵循广义的Benford定律,然后利用首数字直方图用于双重JPEG 压缩检测。然而,一些AC 通道的系数分布并不能很好的遵循该定理,Li 等人[4]提出选择一些特定AC 通道的量化系数并利用首数字特征解决该检测问题。遗憾的是,上述两种基于首数字的方法在质量因子大于95时,检测性能会显著降低。这是因为单次压缩和双重压缩图像的首数字直方图分布的差异较小。Giudic 等人[5]通过对DCT 系数首数字的深入分析,指出通过1-D 的DCT 变换得到的首数字特征用于双重压缩检测要比2D 的DCT 变换更加有效。
不同于上述基于手工特征的方法,一系列基于CNN 的方法近些年被提出,显著提升了双重JPEG压缩检测的性能。Park等人[6]对网络进行训练时考虑了不同类型的量化表,并将DCT 系数直方图和量化矩阵同时作为网络的输入,能够适用于混合质量因子的双重压缩检测。Ahn 等人[7]提出一种端到端包含3D 卷积核的网络结构,使用反量化系数直方图以及利用特征尺度改变策略结合量化矩阵训练该网络。Hussain 等人[8]提出一种两阶段的检测小尺寸图像块双重压缩的方法。第一个阶段采用具有64个核的DCT辅助层,第二个阶段是由多个卷积块组成的深度网络,能够更加有效的提取DCT 系数信息。
目前,现有方法能够很好解决不同量化矩阵双重JPEG 压缩检测问题,即使对小尺寸的图像块,也能取得较高精度的检测性能。但当第一次压缩时的质量因子大于第二次或两次压缩之间存在缩放、裁剪和旋转操作时,上述两类方法的检测性能会大幅度降低,甚至失效。
当使用相同量化矩阵对图像进行连续压缩时,单次压缩图像和双重压缩图像之间图像内容的变化较小,可利用的统计信息也较少,因此对相同量化矩阵的双重JPEG 压缩检测更具有挑战性。Huang 等人[9]观察到相邻两次压缩图像间不同量化系数的个数在连续的压缩过程中会呈现单调递减现象。在此基础上,设计了一种随机扰动策略用于获得一个与图像相关的阈值。通过比较该阈值和不同量化系数的个数进而识别双重JPEG 压缩。尽管该方法简单有效,但存在两种问题:1)对于一些图像,特别是对于低质量压缩的图像,不同量化系数的个数单调递减的趋势并不明显,因此很难找到合适的系数修改比例,进而导致检测的失效;2)随机扰动策略只是无差别的对任意的量化系数进行修改,然而修改不同位置的系数对检测的结果影响较大。为了解决上述问题,Niu 等人[10]提出一种增强的随机扰动策略,首次指出截断误差是该检测问题的关键,提出只对值为1 和-1 的量化系数进行修改,大幅度提升原始随机扰动策略的性能。以上基于随机扰动策略的方法的不足是检测结果具有随机性且不平衡。Yang等人[11]发现在JPEG 压缩过程中,对于存在取整或截断误差的图像块,单次压缩图像中误差的最大值和平均值要大于双重压缩图像。然后,分别利用直流(Direct Current,DC)和AC通道取整和截断误差的方差和均值当作13-D 特征进行检测双重压缩。Niu 等人[12]将用相同量化矩阵重复压缩的过程简化为反量化系数Zk的链,如图2所示。其中Q&D 表示量化和反量化过程,k表示压缩次数。通过理论分析得出图像连续压缩时误差分量和量化系数分量随着压缩次数增加趋向于收敛,最后从误差和量化系数分量分别提取用于检测的15-D 特征。由于对彩色图像进行JPEG 压缩时需要从RGB 空间转换到YCbCr空间,在此过程中会出现转换误差。Wang 等人[13-14]提出利用颜色转换误差检测彩色图像相同量化矩阵的双重JPEG 压缩检测。
若干基于CNN 的方法也陆续被提出用于相同量化矩阵双重JPEG 压缩检测任务。Huang 等人[15]将JPEG 压缩中的误差作为CNN 的输入得到62-D特征,最后合并文献[11]中的13-D特征用于检测双重JPEG 压缩。与文献[10]中的方法不同,Harish等人[16]使用连续压缩产生的误差与其对应的DCT 系数作为网络的输入。现有相同量化双重JPEG 压缩检测的方法的汇总如表1所示。可以看出特征维度在逐渐增加,分类器由传统的SVM 逐渐向深度网络过度,检测的对象也由灰度图扩展到彩色图像。虽然相同量化矩阵的双重压缩检测已经取得了较大的进展,但现有的大多数方法并没有充分利用单次和双重JPEG 压缩之间的统计差异,进而限制了双重压缩的检测性能,特别是对于低质量因子的情况。此外,现有方法缺乏对JPEG 压缩中截断误差和量化系数的理论分析,填补这些空白将有助于进一步提升检测的准确率。
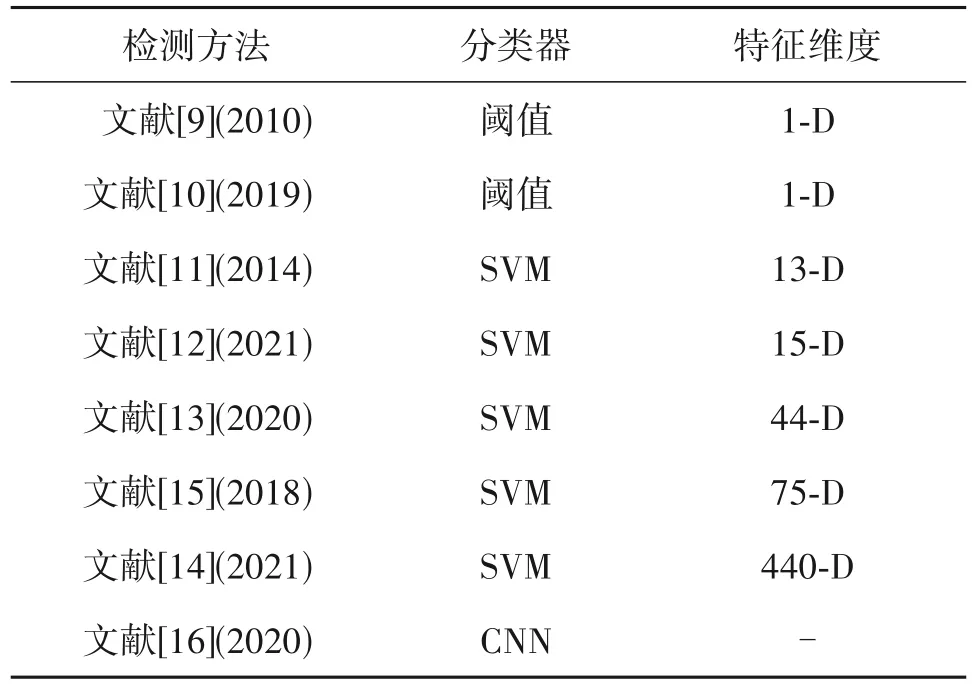
表1 相同量化矩阵的双重JPEG压缩检测方法汇总Tab.1 Summary of detection methods for double JPEG compression with the same quantization matrix
3.2 量化矩阵估计
对JPEG 图像进行解压缩以及重复对JPEG 图像压缩时,解压缩图像的量化矩阵和双重JPEG 压缩图像中第一次的量化矩阵通常无法从JPEG 头文件中直接获取,因此估计上述两种情况下的量化矩阵将有助于进一步的取证分析。
由于解压缩JPEG 图像的DCT 系数分布与量化步长有关,如图3 所示。图中为质量因子QF=85 时通道(1,4)对应量化步长为5的DCT系数分布,从中看出系数主要集中于量化步长的整数倍范围以内。因此,可以从DCT 系数直方图中估计到量化步长。Luo 等人[17]首次对JPEG 压缩中的量化误差、取整和截断误差进行分析,得出DCT 系数主要分布在量化步长倍数[-1,1]范围之内,并指出取整后的DCT 系数绝对值的直方图中对应最大峰值的位置即为量化步长。另外,Luo 等人[17]还发现使用相同的量化表对解压缩图像进行重复压缩,图像像素改变较少,基于这个发现,通过比较重复压缩前后像素的改变量估计量化矩阵。Yang 等人[18]提出了因子直方图的概念,并指出量化步长对应的位置因子直方图出现局部极大值。
Li 等人[19]通过对连续JPEG 压缩中误差的研究,定义了前向量化误差并指出该误差的方差局部极小值的位置对应于真实的量化步长。不同于上述基于直方图的方法,Thai 等人[20]提出一种基于数学分析的方法。该方法对不同的图像尺寸和质量因子均具有较好的估计性能。Yang 等人[21]发现量化表中不同位置的量化步长存在相同的值,如图4所示。依据这种先验知识,提出一种通用的基于聚类的量化矩阵估计框架,实现了对现有估计方法性能的进一步的提升。
对于从双重JPEG 压缩图像中估计初次压缩的量化矩阵问题,Farid[22]通过估计质量因子(Quality Factor,QF)进而间接地估计量化矩阵。然而,这种方法缺失一般性,因为QF 不是标准的JPEG 压缩参数,对于使用专有量化矩阵的压缩软件,例如Photo⁃shop,QF 可能没有定义。另外,还有一些基于模型的估计方法[23-26],该类方法通过利用DCT 系数分布模型,或者双重JPEG 压缩过程中产生特殊的模式进行量化矩阵估计。而另一些方法则是揭示由连续量化引起的特殊效应来估计量化矩阵。以上大多数估计方法在特定的场景下能取得较好的性能。但有些方法只适用于初次压缩质量因子QF1大于第二次压缩的质量因子QF2的情况。还有些方法只适用于第二次压缩的DCT 网格对齐或者非对齐于第一次压缩。例如,文献[22]在第一次压缩的量化步长是第二次压缩的因子时将失效。尽管文献[23]能够同时适用于对齐和非对齐压缩方式,但当QF1>QF2时,估计的性能会大幅度降低。文献[26]只有在QF1 JPEG 图像拼接伪造可以分为三个步骤,如图6所示。首先对质量因子为QF1的JPEG 图像B 进行解压缩,然后使用A 中的一部分区域替换B 的内容,最后使用质量因子QF2对伪造图像C 进行压缩。伪造图像的真实区域和拼接区域会呈现出统计特性不一致性。由于拼接会在DCT 域,特别是在JPEG 系数直方图上留下特殊的痕迹,若干检测算法都侧重于分析JPEG 系数直方图的统计量。而在非对齐的双重JPEG 场景下,双重JPEG 检测的方法往往从像素域或DCT 域提取特殊的特征。然而这些方法都是用于检测整幅图像是否经历过双重JPEG 压缩,不适用于篡改区域的定位。尽管一些基于CNN 的方法能够对小尺寸的图像块检测双重JPEG 压缩且具有较好性能,但是这些方法都是针对双重JPEG VS 单次JPEG 场景。例如,文献[31]用于对齐和非对齐的双重JPEG 压缩检测,文献[6-7]只用于对齐的双重JPEG 压缩检测。也就是说,这些方法假设篡改区域经历了单次JPEG 压缩,而背景则是经历双重JPEG 压缩。相反,更具挑战性的是双重JPEG VS 双重JPEG 场景。目前只有少量的工作关注这个场景。原则上,估计双重JPEG 压缩图像中第一次压缩时的量化矩阵的方法可以应用于此场景。但是,这两种方法都是针对整幅图像,因此它们也不适用于篡改区域定位。文献[32]提出了一种检测图像局部是否经历低质量因子JPEG 压缩的技术,但该方法只限制在QF1 其中Xs和Xd分别表示为单次和双重JPEG 压缩图像的DCT 系数分布,α1和α2(α1+α2=1)分别表示拼接区域与真实区域的比例。通过求解公式(5)可以得到每个DCT 块为双重压缩的概率。但该方法适用于对齐方式的双重JPEG 图像的场景,对非对齐双重JPEG 压缩图像则无效。以上两种方法在当第二次压缩的质量因子大于第一次的质量因子时,即QF1 JPEG 图像被动取证中使用的数据大多是由未压缩图像进行压缩、解压缩、重复压缩等生成JPEG解压缩图像、双重JPEG 压缩图像等。未压缩图像主要来自UCID[38]、RAISE[39]和Bossbase[40]数据库,其中UCID 包含1338幅TIF格式的彩色图像,RAISE包含8156 幅高分辨率的TIF 格式的彩色图像,Boss⁃base 包含10000 幅PGM 格式的灰度图像。上述数据库中的图像还需要进行裁剪或缩放、拼接等操作生成伪造的JPEG 图像用于训练和测试检测和定位模型。 双重JPEG 压缩检测的衡量指标包括真正类率(True Positive Ratio,TPR),即双重JPEG 压缩图像被正确识别的比例、真负类率(True Negative Ratio,TNR),即单次JPEG 压缩图像被识别的比例和准确率,即所有正类和负类被正确检测的比例(当正负样本数目相等时,准确率表示为(TPR+TNR)/2)。当准确率高且TPR 和TNR 之间比较均衡时表明检测方法具有较好的性能。 通常评估量化步长估计的标准为准确率和MSE。准确率为被正确估计的量化步长所占的比例。MSE的计算方式如下所示: 其中x为双重JPEG 压缩图像,N为量化步长的维度,qi和分别表示为第i个真实的量化步长的值与估计的值。MSE越小,表明估计性能越好。 JPEG 图像篡改区域定位结果评估的指标通常为F1分数、马修斯系数(Matthews Correlation Coeffi⁃cient,MCC)和受试者工作特征曲线(Receiver Oper⁃ating Characteristic Curve,ROC 曲线)。F1分数的计算方式表示为: 其中precision 为精确度,recall 为召回率。F1分数的范围为[0,1],分数越大说明定位结果越好。MCC的计算方式如下所示: 其中,TP、TN、FP 和FN 分别表示为真正类数、真负类数、假正类数和假负类数。MCC 的范围为[-1,1],当该指标取值为1 时表示能够完美定位篡改区域,取值为0 时表示检测的结果还不如随机预测的结果,-1 是指预测分类和实际情况完全不一致。ROC 曲线是反映敏感性和特异性连续变量的综合指标,评价其质量的一个重要的特征是曲线下方的面积(AUC)。当AUC 为0.5 时为随机分类,表示分类器没有识别能力,AUC 越接近于1 表示分类器的判别能力越强。 本节首先给出了文献[9-12]中所提方法在UCID(彩色图像首先转为灰度图)上的相同量化矩阵的双重JPEG 压缩检测性能对比,如表2所示。可以看出当质量因子大于90 时,四种方法的准确率均高于92%。当质量因子低于80 时,各种方法的检测性能明显降低,这是因为相当一部分图像的两次压缩之间在空域和DCT 域几乎没有统计差异,因此很难进行区分。而文献[12]同时考虑了误差和DCT 系数分量,整体性能要优于其他三种方法。 表2 相同量化矩阵的双重JPEG压缩检测方法性能(准确率)对比Tab.2 Performance(Accuracy)comparison of detection methods for double JPEG compression with the same quantization matrix 接着,表3 列出了文献[25-26,29-30]中所提方法在RAISE 数据集上初次量化矩阵估计的性能对比,其中测试图像的大小为64×64,第一次压缩的质量因子QF1={60,65,70,75,80,85,95},第二次压缩的质量因子QF2=90。当QF1=95 时,基于模型的传统方法[25]已经失效,而基于CNN 的方法依然具有较好的估计效果。由于文献[25]中的模型不依赖于两次压缩间质量因子而是从量化步长对中学习DCT 系数分布,因此能够更好的获取第一次压缩时量化步长的信息。 表3 双重JPEG图像中初次量化矩阵估计性能(准确率)对比Tab.3 Performance(Accuracy)comparison of primary quantization matrix estimation in double JPEG compressed images 最后,本节给出了基于DCT 系数分布差异性[33-34]和基于异常检测方法[37]对JPEG 图像拼接检测和定位的性能对比实验,如表4 所示。实验的数据集为文献[33-34]中使用的部分图像,分别表示为Db 和Dw。其中,Db 中图像的分辨率为1024×1024,第一次压缩的质量因子QF1∈{50:5:100},篡改区域部分为图像总面积的1/16 且为中心区域。Dw 是由UCID 中图像生成,第一次压缩的质量因子QF1∈{55:10:95},篡改区域部分为图像总面积的1/10。两种数据集中图像均为对齐方式的双重JPEG 压缩且第二压缩的质量因子QF2=90,对比结果如表4 所示。可以发现文献[34]所提方法要优于其他两种方法,这是因为该方法[34]针对对齐方式的双重JPEG图像而设计。另外,两种数据库中篡改区域没有明显的拼接痕迹,使得文献[37]中基于异常检测方法的优势并未体现出来。 表4 JPEG图像篡改定位(MCC)对比结果Tab.4 Performance(MCC)comparison of JPEG image tampering localization 在过去的几十年中,JPEG图像被动取证的研究已经取得了一定的进展,也体现出很大的发展潜力和应用前景,但是当JPEG 图像取证技术在推向实际应用中依然面临一些问题。 (1)彩色双重JPEG 压缩图像检测方法缺乏误差的理论分析。不同于灰度图像,彩色图像进行JPEG 压缩时需要将RGB 空间转换到YCbCr 空间,因此压缩产生的误差也不同于灰度图像。另外,颜色转换时也会引入一些误差,如何建立理论模型、有效的分析和利用这些误差能够提升双重压缩检测的实际应用价值。 (2)量化矩阵估计方法面临的主要问题是当存在后处理操作时,例如裁剪、缩放等,该类估计方法的性能会大幅度降低,甚至失效。这是由于后处理操作能够破坏JPEG 压缩痕迹,进而很难从DCT 系数分布中估计量化矩阵。一种解决思路是首先估计裁剪的偏移位置或者缩放因子,然后根据偏移位置估计第一次压缩的DCT 系数分布或者根据缩放因子逆向的缩放图像进而恢复第一次压缩的信息。另一种思路是利用强大的CNN 网络结构学习经过后处理操作留下的特殊痕迹,从而获取更多的压缩参数信息。 (3)目前JPEG 拼接图像定位通常看作二分类问题[41],即识别拼接区域和真实区域,如何区分多个拼接区域的归属、追溯其来源[42]等问题需要进一步解决。解决的思路根据量化矩阵不一致性结合聚类的思想对拼接区域进行归属判别。另外同时利用拼接边缘差异性和拼接区域的统计特性不一致性能够进一步提升定位性能。 本文对现有JPEG 图像被动取证方法进行了综述和回顾。首先重点介绍了双重JPEG 压缩检测、量化矩阵估计和JPEG 图像拼接检测定位的关键技术并对存在的问题给出了解释说明。其次对取证技术验证使用的数据集及性能评测指标进行了描述。接着对JPEG 图像双重压缩检测和量化步长估计等方向现有方法进行了对比和评价。最后指出了现有方法面临的问题并给出了对应的解决思路。由于伪造方式的多样性,现有的取证方法往往只适用于单一方式下生成的伪造图像,利用多种取证手段和融合多个取证方法的结果能够进一步提升取证方法的精度。虽然基于深度学习的方法已经成为数字图像取证的主流趋势,但是目前伪造图像的数量远远小于真实图像,生成海量多样性的伪造图像用于训练深度网络能够增强模型的鲁棒性和泛化能力。3.3 JPEG图像拼接检测与定位
4 数据集与评价指标
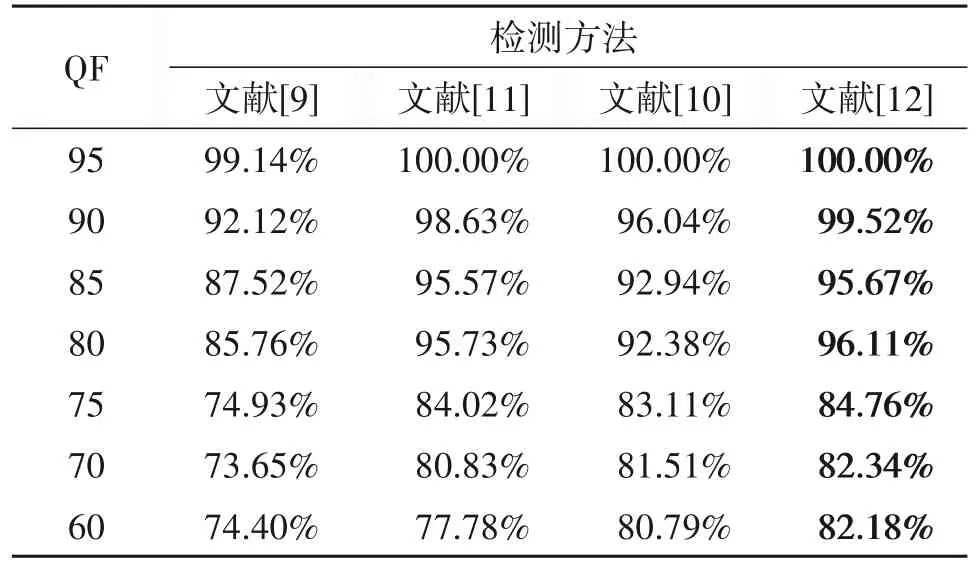
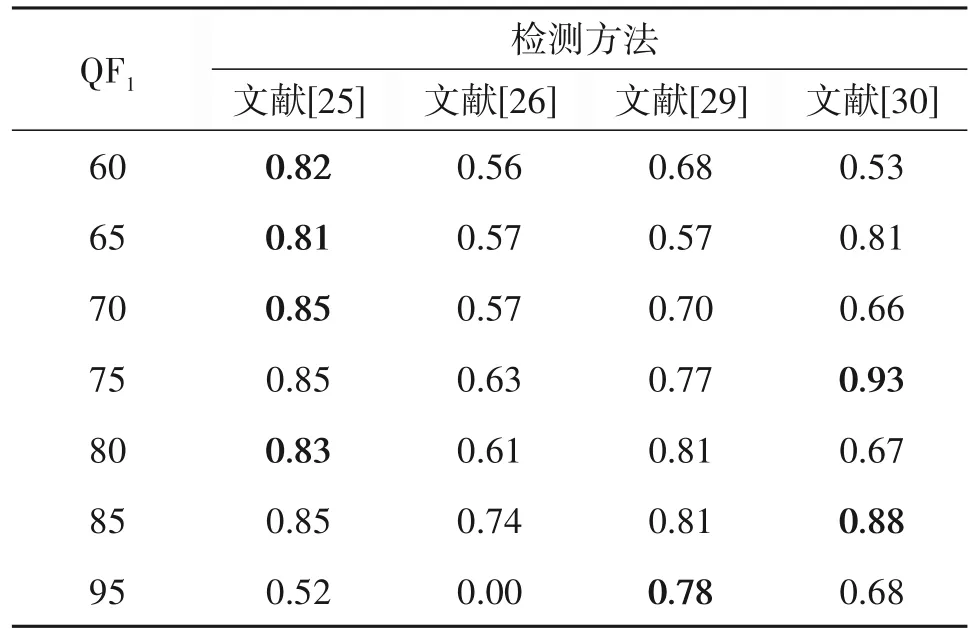
5 性能对比

6 存在的问题与解决思路
7 结论
