基于自校验孪生神经网络的故障区段定位方法*

2022-07-21李松浓侯兴哲付秀元

电子技术应用 2022年7期

王毅，李曙，李松浓，陈涛，侯兴哲，付秀元

（1.重庆邮电大学通信与信息工程学院，重庆 400065；2.国网重庆市电力公司电力科学研究院，重庆 400014；3.国家电投集团数字科技有限公司，北京 100080）

0 引言

我国中压配电网主要采用中性点非有效接地方式。单相接地故障作为小电流接地系统中发生频率最高的故障，一旦发生，由于其电气物理特征并不明显，并且故障电弧的燃弧不稳定；与此同时，配电网的运行方式灵活多变，不同线路结构差异较大，使得故障情况较为复杂，为小电流接地系统的故障检测带来了极大困难。

单相接地故障检测主要由故障识别、选线、定位和测距四部分构成。其中快速准确地实现故障定位能保证故障能及时处理，提高电力系统的供电可靠性。经过近几年国内外的研究，故障选线技术已经日益成熟，并且已经在实际应用中取得了不少成果，为后续确定故障区段或故障点距离打下了良好基础。而故障定位中诸如信号注入法[1]、中值电阻法、阻抗法[2]、行波法[3-4]等技术受配电网分支多、结构复杂、现实路径阻抗和系统运行方式等原因影响较大，并且运行与维护成本较高，对某一故障点进行距离演算的技术其实用性都有待考量。

故障区段定位可以进一步缩小故障查找范围，是实现故障测距与精确定位的前提，这类方法依附于目前先进的通信技术，各馈线终端先实现故障信息上传，主站再结合配电网结构与特征信息构建故障判别矩阵，并通过检测算法确定最终区段[5]，有良好的工程实用价值。

该定位技术主要是利用零序电流比较法或相关法来确定故障区段的，通过比较故障点上下游暂态信号的相似性（极性或幅值）可以判断出故障区段与健全区段。该方法虽然简单，但是对检测装置的同步条件有一定要求，并且在实际情况中，无论是设备的错误安装还是系统本身的某些特殊位置，都可能使得算法存在定位盲区，造成误判。传统的线性相关法主要计算信号之间的相关系数，但是判定结果容易受到互感器反接或者故障点距离的影响。目前许多学者从故障点两侧的暂态电流幅值特征入手，引入某些距离算法来识别幅值差异[6]，但是这类方法对异常数据的抗干扰能力弱[7]。以上方法在实际工程中往往需要人为调整判决阈值以提高现场和检测设备的精确度，引入了人工干预，并且对研究人员的经验要求较高[8]。

本文将广泛用于图像识别的孪生神经网络（Siamese Convolutional Neural Network，S-CNN）引入配电网的区段定位，提出一种基于平稳小波变换（Stationary Wavelet Transform，SWT）自校验的配电网故障定位新方法。首先分析了系统中各类不利因素对于上下游暂态波形的相似性和极性关系的影响，并利用小波模极大值和多尺度特性提高信号同步精度和抗干扰能力；然后将预处理后的暂态波形送入神经网络进行训练，利用卷积神经网络提取故障信号的潜在特征，并将特征向量的欧式距离作为输出完成整个自适应学习。经检验，所提方法对于不同环境和人为干扰都有较强的适应性，并且可以克服传统线性相关法存在故障盲区点无法识别的问题。

1 小电流接地系统零序电流暂态特征分析

1.1 小电流接地系统暂态零序电流分布

小电流接地系统在发生单相接地故障时的暂态零序等效网络如图1 所示。开关K 可以切换系统的接地状态，L 为消弧线圈；每个线路区段由线路中串联的单元阻抗Z0和对地并联电容C0jm构成，其中F 点为故障点，当发生单相接地故障时，相当于在该点施加一个虚拟电源U0f，其故障电流i0f从线路流回母线，i0f1和i0f2分别表示经故障点流向上游和下游的零序电流；i0j表示各线路出线端的零序电流，i0jm表示流经并联支路的零序电流；智能故障指示器Djm能采集当前节点的零序电流，并将线路j 分为若干个最小区段。

图1 单相接地故障时的零序等效网络

故障点上游的零序电流为所有非故障线路零序电流、故障线路检测点上游分布电容电流和消弧线圈补偿电流之和，而故障下游的零序电流为故障点下游到负荷端的分布电容电流。当线路n 在故障指示器m 与m+1之间发生单相接地故障时，故障点上下游零序电流表达式如下：

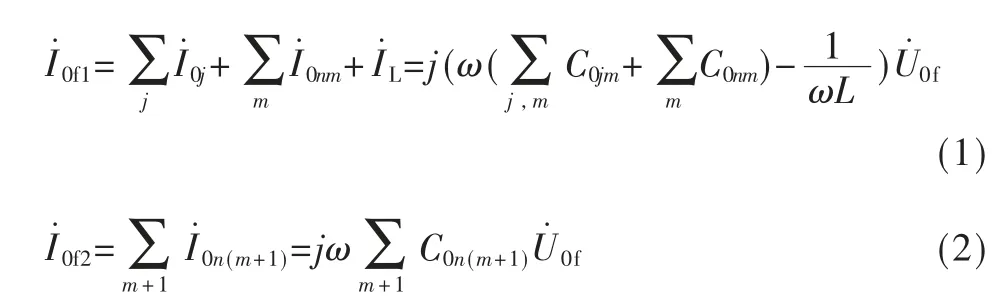
当消弧线圈处于过补偿状态（5%～10%）时，故障点上游的电流呈感性，由于暂态过程中消弧线圈等效阻抗远大于串联线路阻抗和并联对地容抗，且属于高频分量，因此暂态过程可以忽略其补偿作用[9]。通过式（1）、式（2）可知故障点上游的暂态电流大于故障点下游，且两者极性相反，即故障区段的零序电流相似度性低。而对于故障点同侧，越靠近母线或者负荷远端，其幅值越小，由于两个相邻检测点之间的距离一般较短，即对地电容电流较小，因此故障点同侧相邻节点所采集的零序电流相似度极高。

1.2 故障暂态零序电流的相关性分析

根据图1 所示的零序等效网络，无法对上下游的暂态电流进行进一步解析，因此采用集中式参数取代分布式参数，并通过Γ 模型构建如图2 所示的零序等值电路。在发生单相接地故障时，消弧线圈的补偿作用主要体现在工频稳态分量，因此进行暂态分析时可以忽略这部分电路。

图2 配电网零序等值电路

图2 中，C0b为故障点上游和健全线路等效对地电容，R0b和L0b为母线到故障点的等效电阻和电感；C0l、R0b和L0b为故障点下游从故障点到负荷端的等效电容、电阻和电感；uf是故障点的等效电源。根据图2 以及文献[10-11]，其故障点上下游零序电流的暂态分量瞬时表达式为：

式中：ωx、αx和δx分别为i0x的自由振荡频率、初相位和衰减系数；Um为系统相电压的峰值；ω 为工频频率；φ 为故障时刻的初始相角；下标x 取b 或l 时分别代表故障点的上下游。在同一条电气参数均匀分布的线路上，故障点上下游的零序电流具有相同的衰减系数，因此表示两者的相关系数ρbl为：

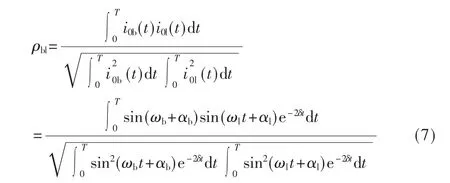
对于线性相关法，相关系数取值范围为0≤|ρbl|≤1，其绝对值越大，表示两个信号相似度越高，该值受到故障点上下游谐振频率的影响。通过式（3）、式（4）可知，故障点上游暂态零序电流幅值大，振荡频率低，而下游幅值小，振荡频率高[12]。但是当时ωb≈ωl，会使得|ρbl|≈1，造成系统误判。

1.3 区段定位的影响因素

由上述分析，线路中存在某一临界点使得故障点两侧的谐振频率相同。设ωb=ωl，由式（4）可得到表达式：

其中，lb为故障点到母线的距离，lΣ为系统所有线路的总长度，lf为当前故障线路的长度。工程中一般认为故障上下游零序电流的相似满足0.8ωl≤ωb≤1.25ωl，通过上述表达式可以得到代表故障点位置lb的曲面曲线，如图3 所示。两曲面之间区域为可能导致误判的定位盲区，并且在某一系统中，故障线路越长，则lb可取范围越大，即发生误判的概率越高。

图3 不同线路总长度lΣ 和故障线路长度lf 的定位盲区

当处于该临界点时，故障点上下游暂态零序电流具有幅值相等、极性相反、相关系数呈负相关的特点，部分研究人员从极性入手，将ρbl＜0 作为判决条件，但是若出现图1 所示电流互感器（Current Transformer，CT）反接的情况，则可能导致当前故障区段零序电流的幅值与极性均相同，而把下游的健全邻近区段判为故障。

与此同时，过渡电阻对线性相关法同样存在影响。随过渡电阻的增大，暂态零序电流的衰减速率将逐渐增大。虽然电阻大小不影响故障点上下游的波形态势，但是电阻越大，其暂态突变量将减少，因此高阻接地故障时，固定时间内的相关系数会增高而造成原方法失效。

2 基于平稳小波变换的自校验算法

2.1 平稳小波变换

小波变换常用于非平稳信号的故障诊断，近几年在电力保护领域得到了广泛应用。平稳小波变换又称为二进制小波变换，相较于传统的小波变换，它仅在尺度上进行离散化，而对平移参数保持均匀连续变换，保证了其时域的平移不变性，因此能更精确地定位信号的奇异点。

对于平方可积的信号f（t），f（t）∈L2（R），定义其平稳小波变换为：

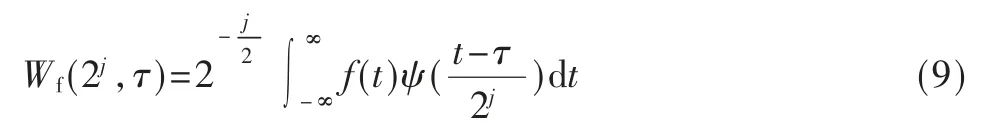
其中，2j为尺度参数，τ 为平移参数，ψ（t）为母小波。

对于某一固定的分解层数j0，若在t0的某一邻域内有，则称点（2j0，t0）为小波变换的模极大值点。由小波变换模极大值与李氏（Lipschitz）指数的关系，其极值点即对应着信号的奇异点，它的极性与幅值分别反映着突变的方向与强度[13]。

2.2 改进的暂态电流自校验匹配算法

大部分被动式的区段定位方法都依赖于智能化馈线终端（Feeder Terminal Unit,FTU）的集中管理，在各个节点发送数据到主站时，FTU 本身的同步误差都进一步限制了故障定位的精度。根据上述分析，可以利用小波变换模极大值理论解决传输终端的信号同步问题。

在实际工程中，配电网常使用消弧线圈过补偿接地方式。往往接地故障发生时暂态过程的持续时间较短，而过渡到工频稳态状态后，由于消弧线圈过补偿会改变故障点上游故障电流的幅值和极性，使故障点两侧的工频零序电流同相，均由母线流向线路，因此在同一条馈线上，其工频稳态分量具有极性的相似性。小波变换具有多分辨率分析的特点，于是对于其分解产生的低频信号，可以通过相关性判断来修正CT 反接等错误安装操作所带来的影响。校验流程如下：（1）计算各检测点小波变换第1 层细节分量的模极大值，进而确定奇异点位置，即故障发生时刻[14]，并实现波形同步；（2）从母线开始逐次校验各线路相邻节点x 与y 的工频分量极性，极性相反则参考相邻的下一个节点z 的极性进行设置；（3）极性按照工频分量的相关系数ρxy进行判断，若ρxy＜0则认为当前信号极性相反，设备x 与y 中存在CT 反接问题需要校验，然后计算ρyz，假如ρyz＜0 就认为节点y出错，如果ρyz＞0 就判为节点x 出错。

3 基于孪生神经网络的区段定位

基于故障点上下游暂态幅值差异的区段定位法相较于线性相关法，可以减少不同中性点接地方式、故障盲区和故障电阻大小对于故障定位的影响。但是该方法还会受到三相不对称引起的虚假零序幅值分量的影响，当接地点的过渡电阻过大或者不对称严重时，可能使得健全区段两侧暂态幅值差异较大而造成误判[15]。

3.1 S-CNN 模型建立

孪生神经网络常用于图像识别，特别在目标追踪、人脸识别中得到广泛应用。网络由2 个分支构成，每1个分支均为1 个CNN，它们网络结构相同并共享权值w。当进行故障检测时，两条分支分别输入线路相邻节点的暂态电流，利用CNN 完成潜在特征提取和降维，并利用特征空间中的距离度量来评价向量差异，最终得到两样本之间的相似度。S-CNN 模型如图4 所示。

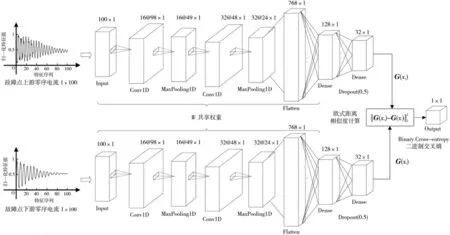
图4 基于一维S-CNN 的故障区段定位模型

（1）卷积层：卷积层主要是实现信号的特征提取，通过指定步长的滑动窗口实现上级输入层的过渡计算，得到下级输出层的卷积特征向量，其表达式为：

（2）池化层：池化层有剔除冗余降低数据维度的作用，并且保留的特征向量具有平移旋转伸缩不变性，其最大池化公式为：

（3）全连接层：在输出结果前，先通过一个延展层进行数据降维，然后经过多个全连接层对具有类别区分性的特征向量进行进一步筛选。由于S-CNN具有训练样本小、重复训练数多的特点，容易造成过拟合，而且不同的CNN 可能产生不同的过拟合，可以通过dropout 技术让部分节点失效并对多网络取平均来提高泛化性。

（4）损失层：通过2 分支网络的前馈传播，得到2 个长度相同的相量G（xb）和G（xl），这里在幅值法的基础上，将两向量的欧式距离作为故障点上下游暂态电流的相似度，其表达式为：

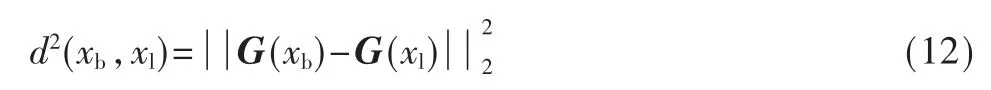
式中，d2（xb，xl）为样本xb与xl的欧式距离，G（x）为前向神经元的计算结果。

为保证两特征向量在相似时欧氏距离尽可能小，差异较大时欧式距离也尽可能大，这里选取二进制交叉熵损失函数，其表达式为：

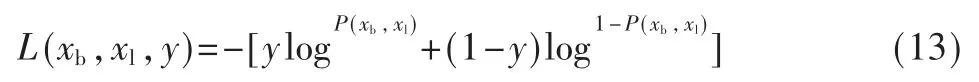
式中，y 为实际的输出，P（xb，xl）为欧氏距离d2（xb，xl）经激活函数Sigmoid 计算的结果，代表两样本之间的差异度，取值范围为（0，1），当健全区段进行判定时，输出差异需尽可能接近0，而发生故障时，上下游暂态故障电流差异较大，输出尽可能为1。

3.2 基于S-CNN 的故障定位流程

图5 是基于S-CNN 的故障定位流程，包含信号的同步校验、模型训练以及测试步骤，具体如下：

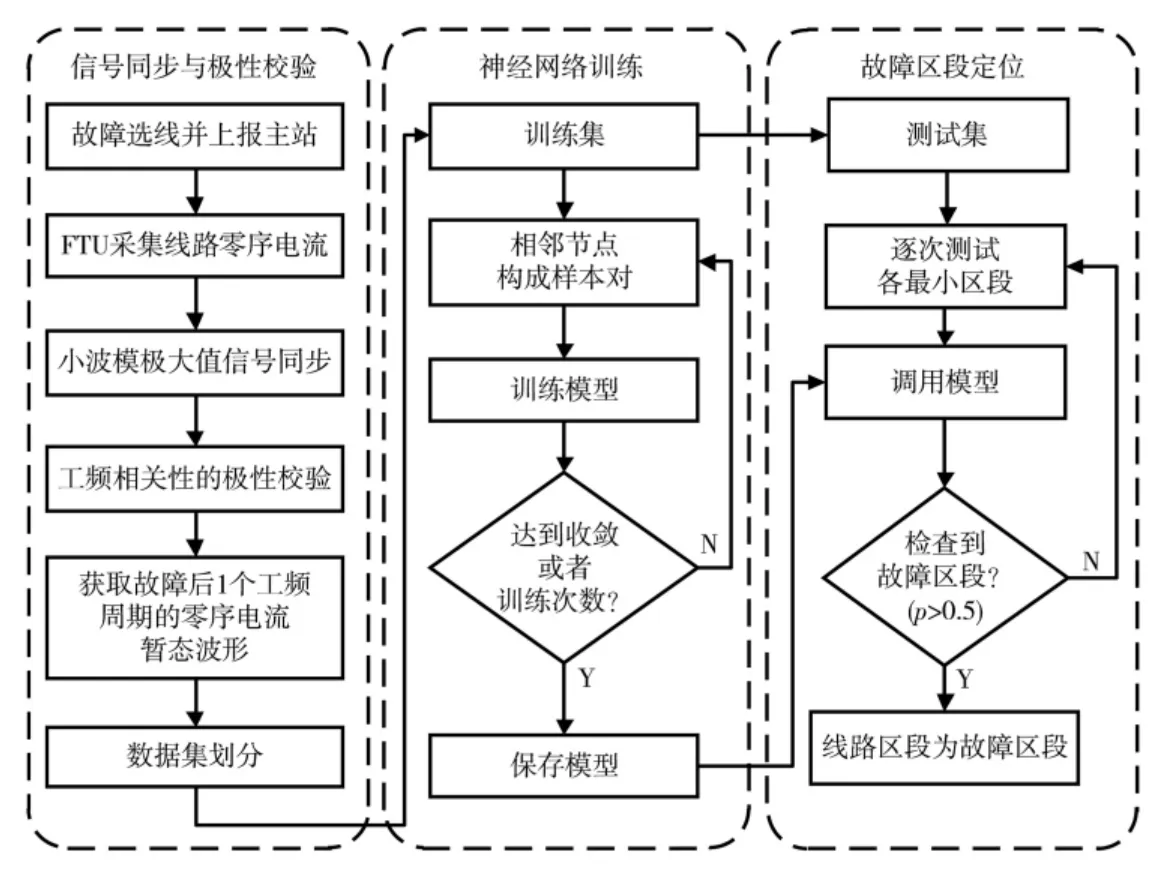
图5 基于S-CNN 的区段定位流程

（1）数据上报与预处理。单相接地故障发生后，根据选线结果，故障线路上的FTU 将采集数据上传至主站进行集中决策，并通过SWT 自校验算法降低通信时延与设备错误安装等因素带来的误差。

（2）训练模型。将训练集中相邻两个节点组合构成最小区段，并取一个工频周期的暂态零序电流作为孪生神经网络的输入，按照式（13）计算损失函数，利用梯度下降算法更新模型。当到达收敛或者达到最大训练次数时停止训练，并导出已训练好的模型。

（3）故障定位。对于某条故障线路，从母线开始从前往后依次测试相邻节点的相似性，输出结果越接近1 表明两者信号差异度越大，确定其为最小故障区段，如果该区段再无支路则结束查找。若该线路上最后一组样本判决结果仍为健全，则认为故障发生在线路末端。

4 仿真结果分析

4.1 系统模型仿真

利用PSCAD/EMTDC 电磁暂态仿真软件搭建如图6所示的2 馈线带分支架空线网络，并利用数字故障指示器DFIx将线路Lx分为10 个最小故障区段Sx，长度为lx，Fx为该区段上所设置的故障点，其中DFI2的CT 极性已被反接。

图6 10 kV 配电网仿真模型

小电流系统中性点由开关K 切换为消弧线圈接地方式，消弧线圈电感过补偿8%（L=14.907 H），每条线路长度分别为L1-1=16 km、L1-2=8 km 和L2=11 km，线路末端预留5 km 作为延长线，线路参数如表1 所示。

表1 线路参数

4.2 自校验算法结果分析

当线路L1-1上距离母线2.5 km 的F2在0.1 s 发生金属接地故障时，获取相邻的检测点DFI1、DFI2与DFI3的零序电流如图7 所示。故障点上游（DFI2）和故障点下游（DFI3）的暂态电流极为相似（已考虑CT 极性反接的情况），并且二者极性保持一致，而故障点同侧的DFI1与DFI2虽然幅值相似，但因为设备错误安装导致极性相反。此时，对在定位盲区与CT 反接共同作用下所采集的暂态零序电流，无论相关法或幅值法都不能有效诊断。

图7 金属接地故障下定位盲区中存在CT 反接的零序电流

按第2.2 节中自校验匹配算法的步骤，先确定故障发生时刻，进行小波模极大值同步，这里的采样频率为5 kHz，采用db3 小波进行6 层分解，对D1 层细节信号进行模极大值计算，得到第一个突变点的时刻为0.100 8 s，根据该时刻实现的信号同步如图8（a）所示。由奈奎斯特采样定理可知其D6 层细节信号所含频带为39～78 Hz，因此选取该层代替工频分量，并计算故障时刻后一个工频周期内的相关系数，计算结果分别为ρ12=-0.999 与ρ23=-0.868，由于ρ12与ρ23均小于0，因此判定DFI2存在错误，需要对其极性进行校验。

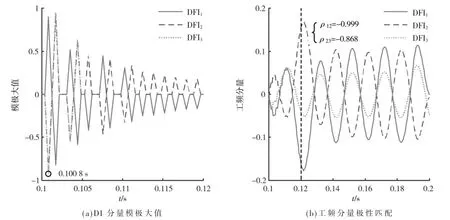
图8 基于SWT 的自校验算法

4.3 S-CNN 模型验证

本文所搭建的S-CNN 网络基于Keras 中的Sequential顺序模型，由多个自定义网络层线性堆叠起来，包含2个卷积层、2 个池化层和3 个全连接层（其中1 个为延展层），其具体参数如图4 所示。

改变接地故障下的过渡电阻大小、初始相位以及故障位置，分别采集图6 中S1～S10区段前后DFIx 的零序电流，经同步校验后截取从故障时刻起第一个工频周期的信号作为神经网络的一组输入样本。其中每个区段采集前后零序电流包含60 组故障状态和540 组健康状态，10 个区段共得到6 000 组样本，随机生成4 200 个训练样本和1 800 个测试样本，并对模型进行100 次迭代。

经过训练，测试集中各区段定位的预测结果如表2所示，总体识别率高达98.8%，其中健全区段和故障区段的平均识别率分别为99.7%和92.8%，证明该方法对于不同条件下故障都有良好的适应性。

表2 数据集构成及各区段预测结果

根据第1.3 节分析，当线路发生高阻接地故障时，由于微弱信号增多，可能会造成传统相关法失效。图9为支路L1-2上区段S6发生高阻接地故障的波形图，接地电阻大小为500 Ω，在进行顺序检测时，传统的线性相关法计算结果为ρ23=0.905，表现为高度相关，从而造成误判无法定位支路故障；而根据S-CNN 计算得到结果ρ23=0.875，差异度大于0.5，即认为S2为故障区段。由于该区段存在分支，因此需要继续判断，进而可以计算最终定位区段ρ67=0.944，实现支路故障S6的定位。