尿素机中高频微弯型科氏质量流量计信号处理
2022-07-21刘陈慈徐科军
刘陈慈, 徐科军, 黄 雅
(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)
1 引 言
通过尿素机添加车用尿素溶液,可与汽车尾气中的NOx发生反应,生成无污染的N2和H2O,从而达到柴油车排放要求。准确计量尿素流量是尿素机计费的核心问题。市场上绝大部分尿素机所用的流量计均为容积式流量计,计量较为准确,但当被测气体或液体受温度或压力影响而改变体积时,易造成较大误差。对于尿素机而言,在寒冷地区计量时易受低温结晶影响;在温度变化较大地区易受热胀冷缩影响而造成较大误差。
科氏质量流量计能够提供高精度和直接的质量流量测量,其测量准确且不受温度与压力变化影响。为了将科氏质量流量计应用到尿素机上,首先要解决尿素机加注液体时的信号处理难点。一方面,尿素机是用启停法加注尿素,由一开始的零流量骤增到最大流量,保持最大流量一段时间后,由加注人员调整加注枪减小流量,末尾阶段最小流量由机器自动加注,多次的流量切换,给科氏质量流量计的动态响应速度提出了较高的要求。
另一方面,为了将科氏质量流量计安装在尿素机上,要求科氏质量流量计的体积小,因此,制造方选用了微弯管型科氏流量计。它的优点是体积小,安装较为容易,不易残留杂质。但是,对信号处理提出了挑战。这是因为微弯型科氏质量流量管的固有频率高,一般大弯管型科氏质量流量管的固有频率为75~150 Hz,国内的微弯型科氏质量流量管的固有频率一般是300 Hz左右,而课题组选用的是600多Hz,必须提高采样频率。而受科氏质量流量变送器芯片运算能力的限制,这就需要研究合适的算法,并要求的运算量较少;微弯型科氏质量流量传感器输出的相位差小,一般是大弯管型的1/9,这使得信号处理难度加大。尤其是在尿素机加注末尾阶段,微弯型科氏质量流量传感器本来相位差就很小,小流量时的相位差则更小,而较小的相位差由于算法运算时间与算法本身的误差,相比较于大相位差而言误差更大。因此,在尿素机上应用科氏质量流量计不仅要求较快的算法跟踪速度,还要求较高的小流量测量精度。
在启停测量与需要较快动态响应速度方面,国内外学者做了许多研究。Clark等认为流量计的动态响应与机械设计、驱动控制以及信号处理等方面有关[1~3],并对一批商用流量计做了动态响应实验[2];Henry等研制了新型数字变送器,当流量发生阶跃式变化时,也能达到较高的精度与较好的重复性[4,5];涂亚庆等对批料流中科氏质量流量计动态响应速度进行了研究[6]。但是,鲜见科氏质量流量计应用于尿素机方面的文献。
为了将科氏质量流量计应用到尿素加注机上,首先根据加注过程中的科氏质量流量计的输出信号,建立相位差变化的数学模型;根据此模型,分析加注过程中的流量变化规律;对比2种工业领域实用效果较好的信号处理方法,选取其中更为适用的算法,并进行改进;研制微弯型科氏质量流量变送器的硬件模块和软件。基于以上系统及改进后的算法,进行水流量标定试验和尿素机加注标定实验,验证方案的有效性与实用性。
2 尿素机加注过程与信号建模
2.1 加注过程
为了分析尿素加注机加注过程中流量的变化,采集加注全过程2路传感器的原始信号,分析2路原始信号的相位差的变化情况。
在理想状态下,科氏质量流量计2路速度传感器输出信号均为频率和幅值相等的正弦信号,它们之间的相位差反映了液体的质量流量。科氏质量流量计在单相流量标定时,在各稳定流量点传感器输出信号的相位差均保持微小的波动。在标定尿素加注机时,当开启而没有加注时,由于离心泵开启,流量会上升到一个较小的波峰然后回零;再开水枪加注时,流量瞬间由零到最大,并保持一段时间;在接近末尾阶段,由加注人员减小流量;在最后阶段,由机器控制至最小流量自动加注。在整个加注过程中,流量多次快速变化,且实际加注现场由于加注人员不同,每次加注时,控制加注枪的动作快慢也不同。如此复杂的流量变化状况,给流量计的准确测量造成较大困难。
为了准确地获取传感器输出信号的变化规律,针对Endress+Hauser公司生产的DN25的F型号科氏质量流量传感器,匹配课题组研制的变送器,进行尿素加注机测量实验。在实验过程中,使用NI公司生产的USB6255数据采集卡实时采集传感器输出信号,经过低通滤波环节对ADC采集的原始信号进行预处理,消除信号中的高频噪声干扰,然后使用合适的算法计算信号的频率和相位差等关键量。基于DSP的科氏质量流量变送器通过串口与MATLAB上的GUI通讯,将实时计算出来的相位差、频率和流量等结果显示在液晶屏幕上。使用NI公司生产的USB6255数据采集卡与传感器原始信号线相连,配合Labview软件采集2路传感器信号。该数据采集卡有效位数16位。使用50 kHz的采样频率采集100 s的原始信号数据,预定加注20 L。总共3个流量档位,每个流量档位测试3次。出于成本考虑,尿素用水代替也能取得同等效果和实验说服力。
2.2 信号建模
用MATLAB编程,对采集的3个档位(大流量档位的最大流量为30 L/min、中流量档位的最大流量为26 L/min、小流量档位的最大流量为19 L/min)的原始信号计算出的相位差。试验在每个档位测试了3次,由于每次加注时的流量变化时间点与变化程度不同,因此,每个流量档位选取了其中一条较为典型的相位差变化情况,如图1所示。然后,对该随时间变化的相位差进行建模。
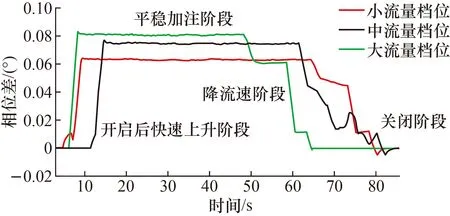
图1 加注过程的相位差变化Fig.1 Phase difference changes during filling process
由图1可知,加注机在开启提枪后,离心泵开启,而此时水枪未开启,由于离心泵的抽水压力冲击,会给科氏流量计1个较小的流量信号,此时水压集聚在水枪口;水枪开启后,流量瞬间到达预设的大、中和小3个档位,保持一段时间的较为稳定的流量;在加注到17 L左右时,加注人员主动减小流量,流量急剧减小;在末尾阶段,加注到接近20 L时,由加注机以最小流量自动加注,直至加注满20 L。
在忽略较小扰动的情况下,尿素机加注可大致分为3个阶段:快速上升阶段、平稳加注阶段和降流速关阀门阶段。可以用一次斜坡函数来表示快速上升阶段的相位差,可以用常数来表示平稳加注阶段的相位差,而在降流速关阀阶段,由于流量频繁变化,无法准确地去描述。具体地,科氏流量计输出信号随时间变化的相位差函数模型如式(1)所示。以中流量档位为例,由t1的接近相位差为0°变化到t2的0.07°左右,是近似斜坡函数的快速上升阶段;由t2到t3维持在0.07°左右,是近似常数的平稳加注阶段。
(1)
式中:t为时间;t1为尿素加注机开启时刻;t2为当前档位流量达到最大的时刻;t3为尿素加注机开始降速时刻;Δθ(t)为相位差;k1为为斜坡函数斜率;h1为为斜坡函数初值;p1为为平稳加注阶段常量。
由图1可见,流量是由从零开始迅速增加,到达该档位的最大值后,保持了一段时间,又较快地跳跃下降,最后缓慢到零。这种动态测量过程,不仅要求科氏质量流量计响应速度要快,信号处理速度要快,更要求小流量的测量精度要高。不考虑安装空间时,常用的大弯管型科氏质量流量计的工作频率一般在100 Hz左右,相位差一般在1°以上。为了缩小体积,制造厂家选用了微弯型的科氏质量流量传感器工作频率高,一般在600 Hz以上,最大相位差在0.1°以内。这对信号处理和驱动提出了更高的要求。
3 信号处理与驱动方法研究
3.1 2种常用信号处理算法的比较
与单相稳态液体测量不同,需根据在加注过程中传感器输出信号的特征,分析已有算法存在的问题。为了准确及时地算出相位差结果,从实时性与准确性2方面出发,将工业中实用效果较好的信号处理方法:DTFT(离散时间傅里叶变换)算法和数字式过零检测算法做了分析比较。
科氏质量流量计传感器信号是2路同频率正弦信号,设其采样序列分别为:
s1(n)=A1cos(ωn+θ1)
s2(n)=A2cos(ωn+θ2)
式中:A1,A2为信号幅值;n=0,1,…,N,N为采样点数;ω=2π f0/fs, f0为信号频率, fs为采样频率;θ1,θ2为信号初始相位值。
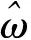
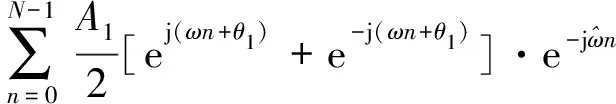
(2)
考虑负频率的影响:
(3)
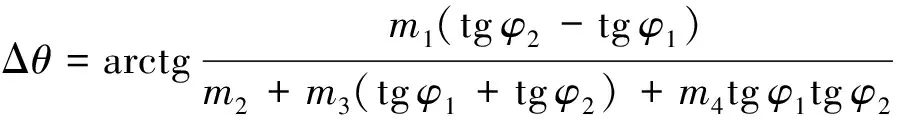
(4)
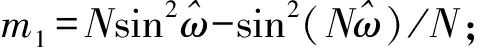
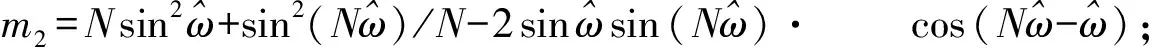
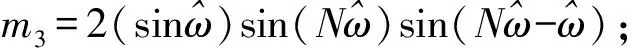
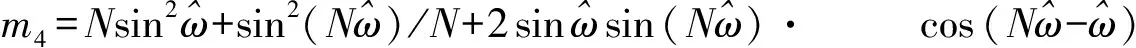
过零检测算法是通过记录信号过零点的时刻,得到过零点间的时间间隔,进而求取信号频率和时间差[7],实现流量测量,如图2所示。由图2可得,信号频率为f=1/(tR3-tR1),2路信号的时间差为Δt=tR2-tL2,相位差为Δθ(t)=360Δtf。
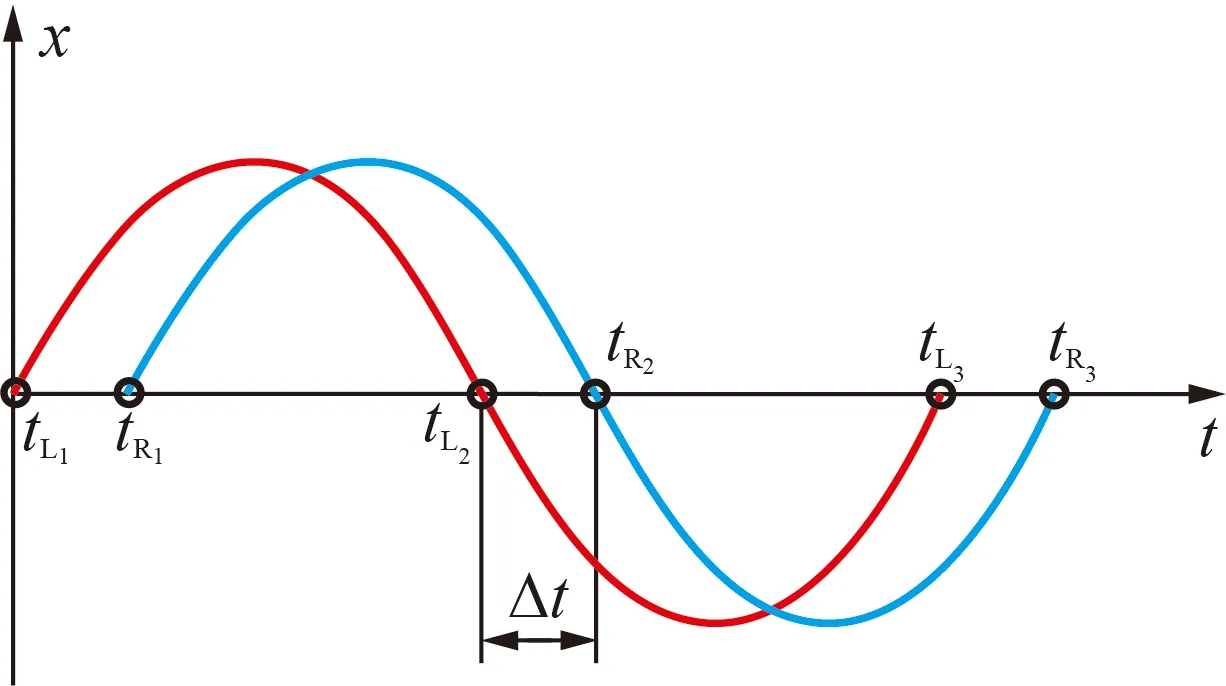
图2 过零检测原理图Fig.2 Schematic diagram of zero-crossing detection
过零检测算法能够准确计算相位差的关键之一是准确找到过零点,寻找过零点按照“采样后数据滤波→粗测过零点→提取过零点附近数据→Lagrange插值法拟合曲线[11]→解二阶曲线方程→得到过零点”的过程进行。
分析2种典型算法的运算量与实时性,选用较为适合的过零检测算法,既能实时反映当时的流量情况,又能保证较高的采样精度。对现场采集的数据进行离线处理,从动态响应速度的角度出发,提出算法改进的办法。
在尿素加注机上使用科氏流量计,要求DSP芯片具有较少的算法运算时间,以满足实时性的要求,这也是标定达到较高精度的必要条件之一。为了减少算法的运算时间,一方面要求DSP具有较快的指令执行速度,另一方面要求较低的算法复杂度。由于DTFT算法每个采样点都参与运算,而过零检测算法只有过零点参与运算。经过不断的测试和大量的实际应用,DTFT算法采样100点调用一次算法,过零检测算法采样500点调用一次算法,能保证相位差的计算精度。
在DSP芯片选型上,选用了TMS320F28335型号,其指令执行速度为150 MIPS(百万条指令每秒),配合外扩的24位高精度数据采集芯片ADS1255,在不同算法、不同采样频率时,算法的执行时间如表1所示。
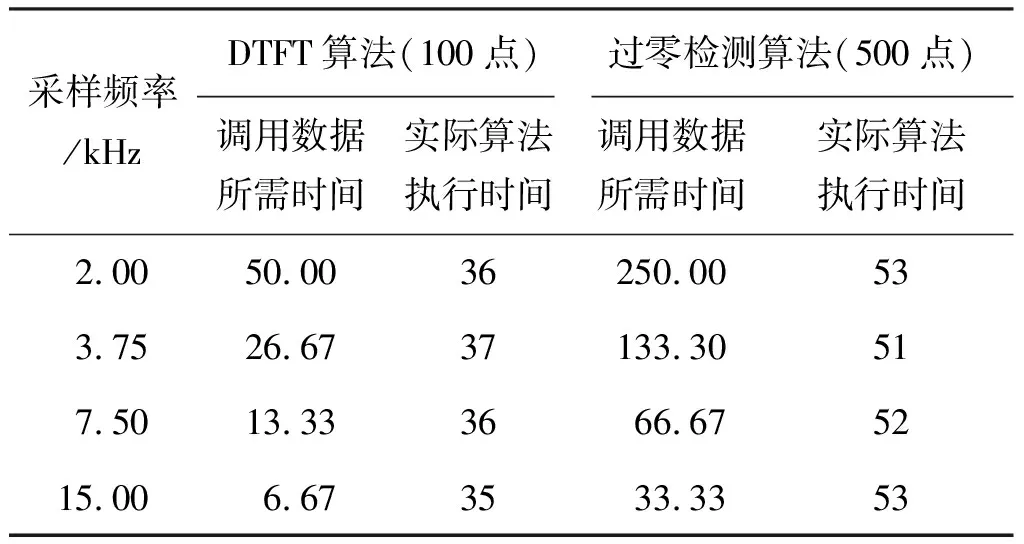
表1 TMS320F28335的处理时间Tab.1 Processing time of TMS320F28335 ms
从表1中可以看出,如果使用DTFT算法,仅 2 kHz 的采样频率算法执行时间少于调用数据所需时间,高于2 kHz的采样频率均会由于运算跟不上ADC采样速率而造成ADC数据采集冗余,实时性下降。如果采用过零检测算法,则可以做到7.5 kHz的采样频率而保证实时性。选用的科氏质量流量传感器满管时的固有频率为667 Hz,为了保证算法精度,采样频率应不低于传感器固有频率的10倍,7.5 kHz的采样频率高于该传感器的满管固有频率的10倍。
如果采用DTFT算法,则只能选用2 kHz的采样频率,而2 kHz的采样频率仅3倍于667 Hz的传感器,远远达不到高精度的要求。而选用过零检测算法可以把采样频率提高到7.5 kHz,达到10倍于传感器固有频率要求;同时,也能保证算法的实时性。因此,选用过零检测算法,同时将ADC采样频率设为7.5 kHz,然后取合适的兼顾较快响应速度与较小相位差波动的折中的滑动平均数组长度Nmean值,理论上标定可以达到较高精度。
3.2 过零检测算法的改进
3.2.1 信号预处理
由于实际工业现场具有许多噪声,例如,随机噪声、电机与管道振动等高频干扰,因此,设置低通滤波来进行信号预处理,截止频率设置为选用的微弯型传感器的满管时固有频率667 Hz,这样就滤除了高频杂波干扰,提高了测量精度。该低通滤波电路为二阶巴特沃斯低通滤波器。巴特沃斯滤波器具有通带和阻带平坦度最大的优点,能够最小限度地降低对信号的影响;二阶滤波器通带以外的频率分量衰减速度快,滤波效果好,且电路简单,仅需一个运放就能实现[12]。
3.2.2 四点插值
为了提高正弦信号零点检测的精准度,对三点拉格朗日插值方法进一步改进,选用了精确度更高的四点拉格朗日插值方法进行曲线拟合。由于正弦信号在零点处的曲线是奇对称的,因此,围绕零点选择4点进行拟合比3点更具有几何上的对称性,其曲线拟合也更加切合实际曲线。当采样序列中相邻2点满足x(n-1)×x(n)<0的条件时,选择零点左右各两点,即x(n-2)、x(n-1)、x(n)、x(n+1)四点进行拉格朗日插值,插值公式为:
(5)
这里采取了反向拉格朗日插值的方法来解决零点计算问题,由于正弦波在过零点处具有较好的线性及对称性,因此,将采样信号的数值与时刻值交换过来进行四点插值计算,即x(n-2)、x(n-1)、x(n)、x(n+1)由因变量变为自变量,4个点的对应下标值由自变量变为因变量。则得到新的插值公式为:
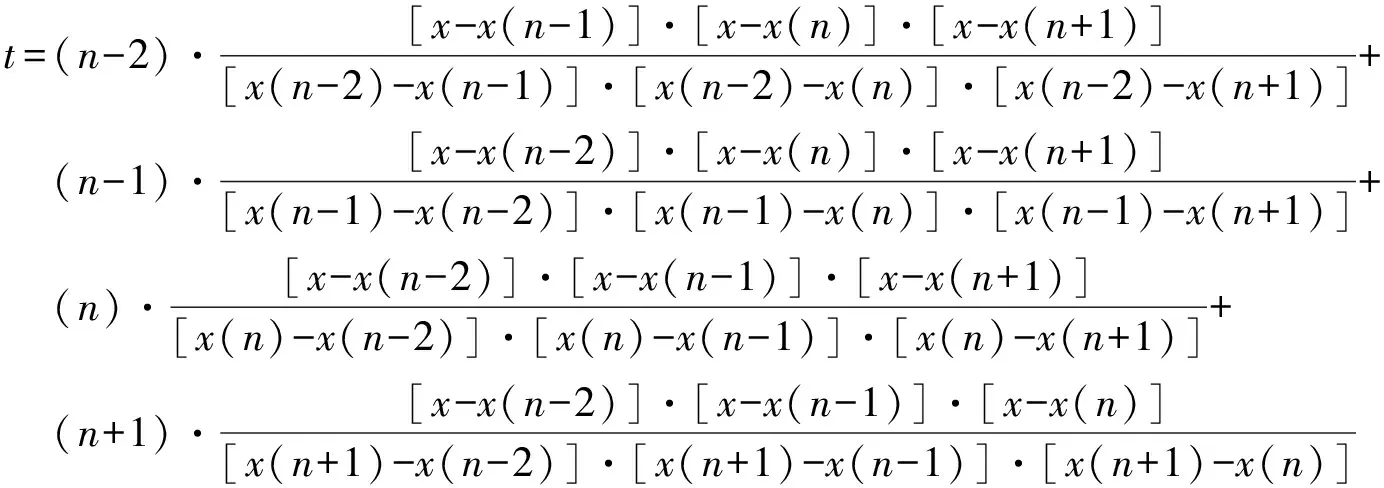
(6)
此时,令式(6)中的因变量x=0,得到t,即为过零点的位置。这种反向拉格朗日插值的方法简单准确,并且避免了求解方程系数以及开方操作引起的大量运算。
3.2.3 相位差后期处理
滑动平均数组长度Nmean是算法中后期数据处理的重要手段。将经过一级平均处理后的相位差保存到该数组中,当保存的数据长度少于Nmean时,只对已保存的相位差取均值;当保存的数据长度一旦达到Nmean时,调动滑动平均处理,对该点与之前保存的Nmean-1点相位差取均值,然后使用此时算出来的相位差代替先前计算的相位差。Nmean就是为了减少奇异点对计算结果的影响。Nmean较大时,能够减少相位差波动带来的影响,显示出来的相位差不会有较大波动,但会影响动态响应速度,不适用于流量频繁变化的场合;Nmean较小时,系统具有较快的算法响应速度,在流量频繁变化时,能快速响应,实时计算显示此时的流量。所以,可通过改变Nmean的值来改变算法响应速度;同时,也要考虑相位差波动带来的影响,以保证测量精度。
使用MATLAB编写过零检测算法,计算采集的原始信号的相位差。依次改变算法后期处理的滑动平均数组长度Nmean=6,8,10,20,从而改变算法的响应速度,结果如图3~图8所示。
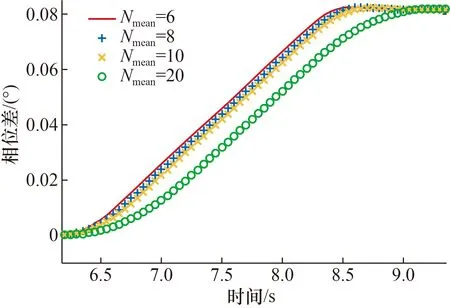
图3 大档位开启过程Fig.3 The opening process of large flow
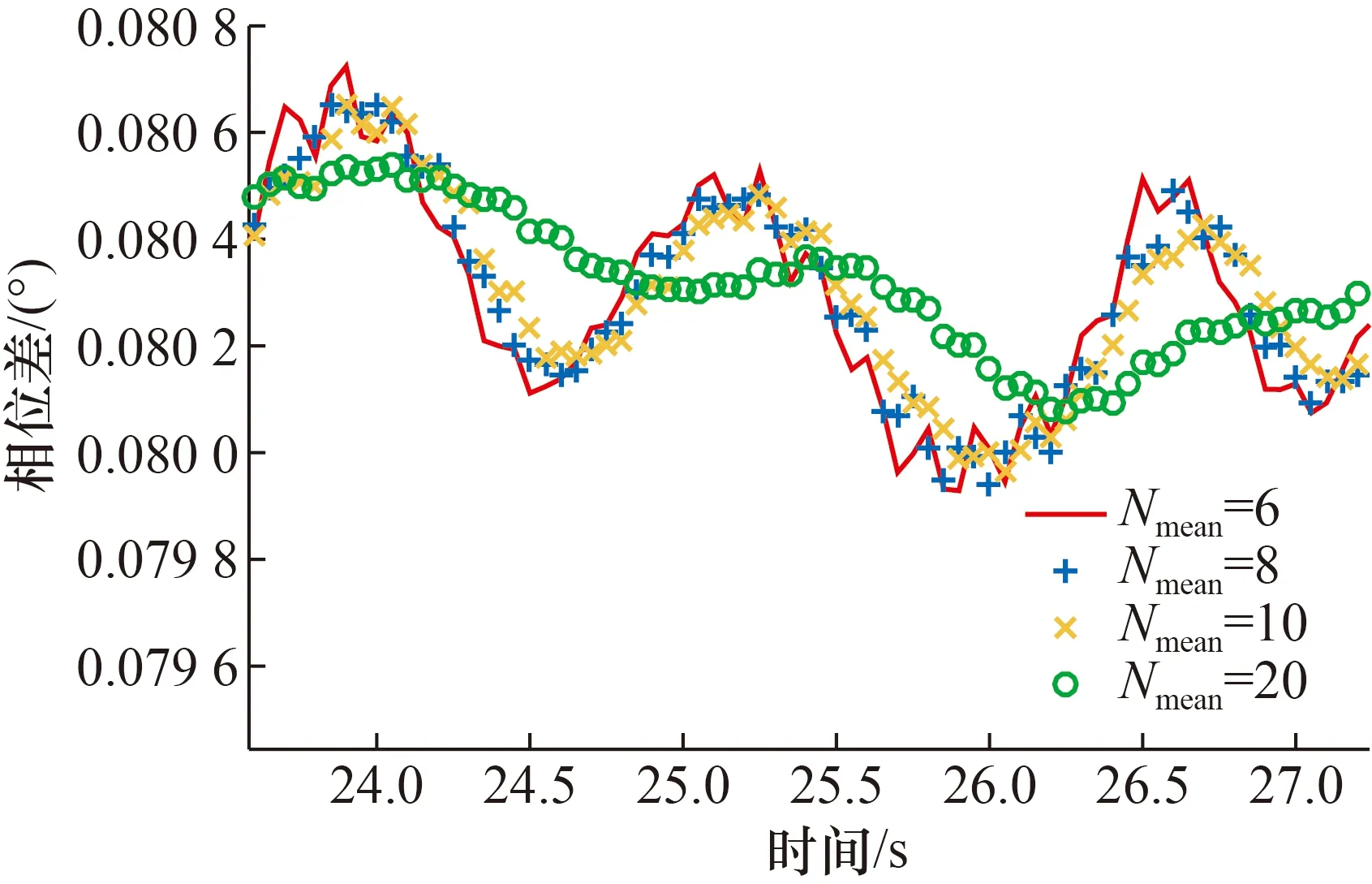
图4 大档位平稳阶段局部放大Fig.4 Enlarging particular sections of large flow in stationary condition
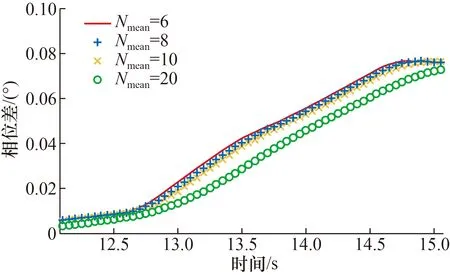
图5 中档位开启过程Fig.5 The opening process of middle flow
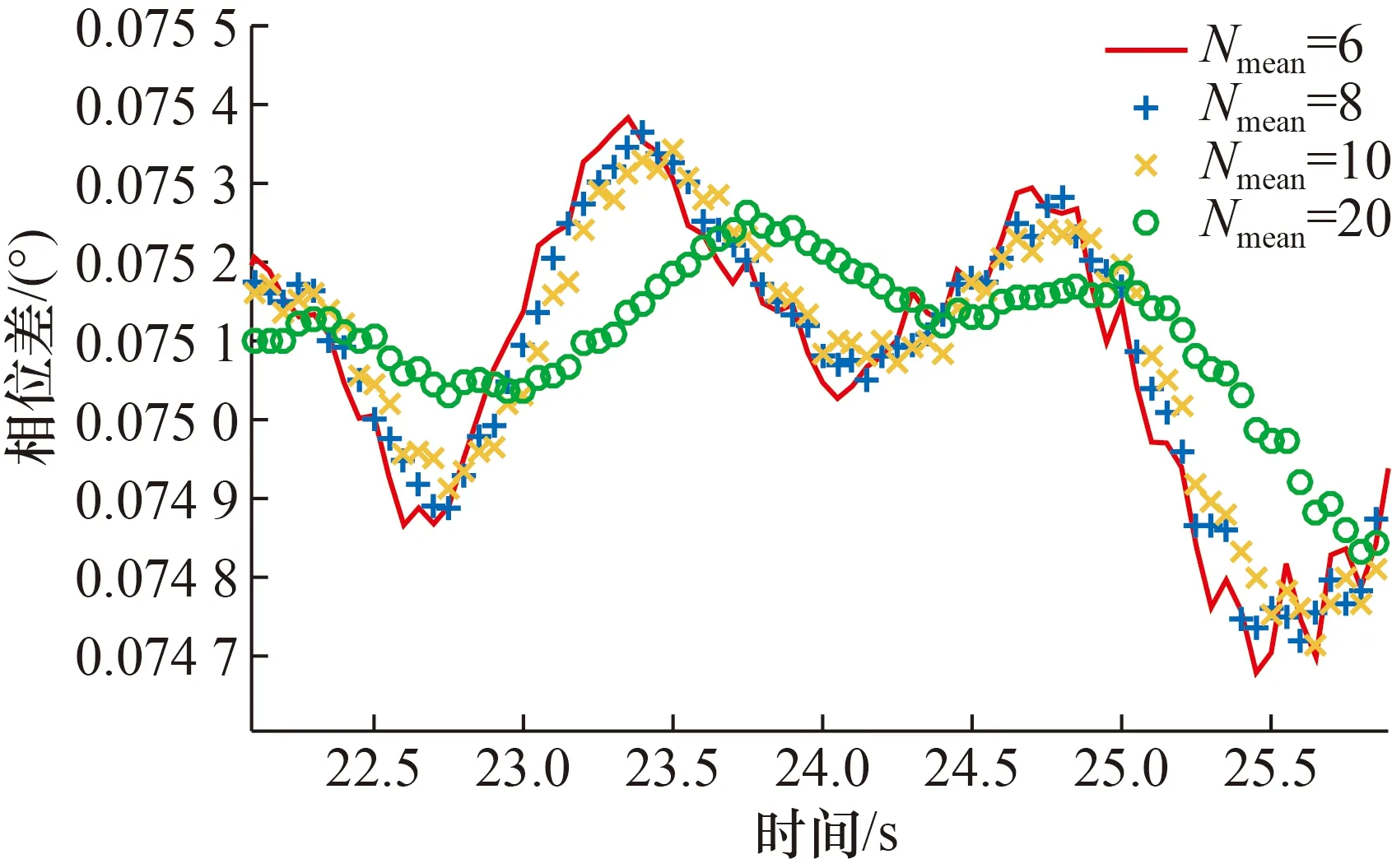
图6 中档位平稳阶段局部放大Fig.6 Enlarging particular sections of middle flow in stationary condition
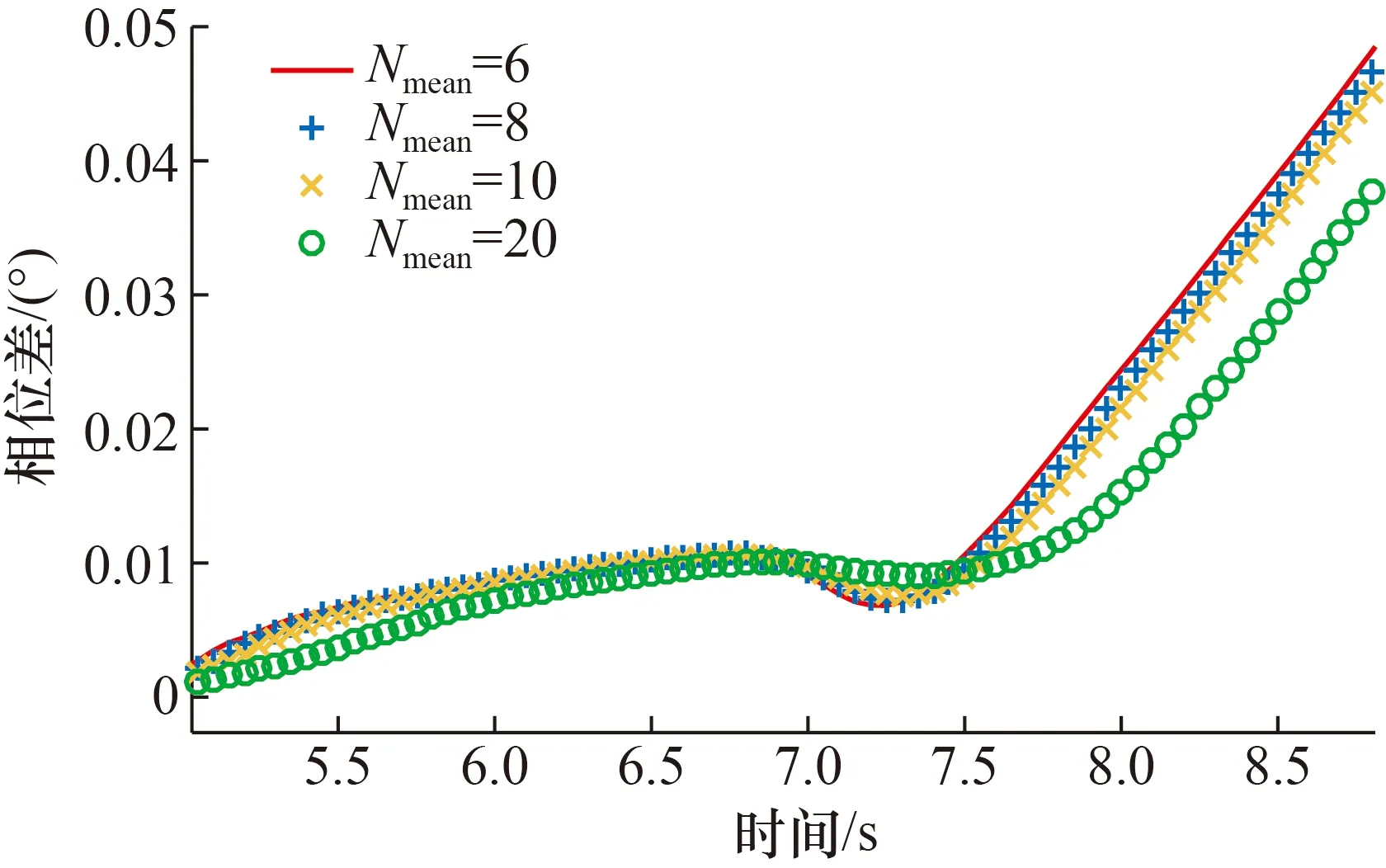
图7 小档位开启过程Fig.7 The opening process of small flow
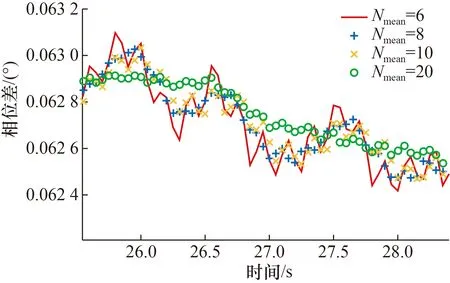
图8 小档位平稳过程局部放大Fig.8 Enlarging particular sections of small flow in stationary condition
从图3~图8可以看出,在不同档位下,在流量开启过程中滑动平均数为6时响应最快,8和10时次之,20时响应最慢。在各档位对应的最大流量的平稳过程中,滑动平均数为6时相位差波动最大,8和10时次之,20时最平稳,波动最小。
为了评估各滑动平均数的测量效果,在大档位下做了实验测试,测试结果如表2所示。
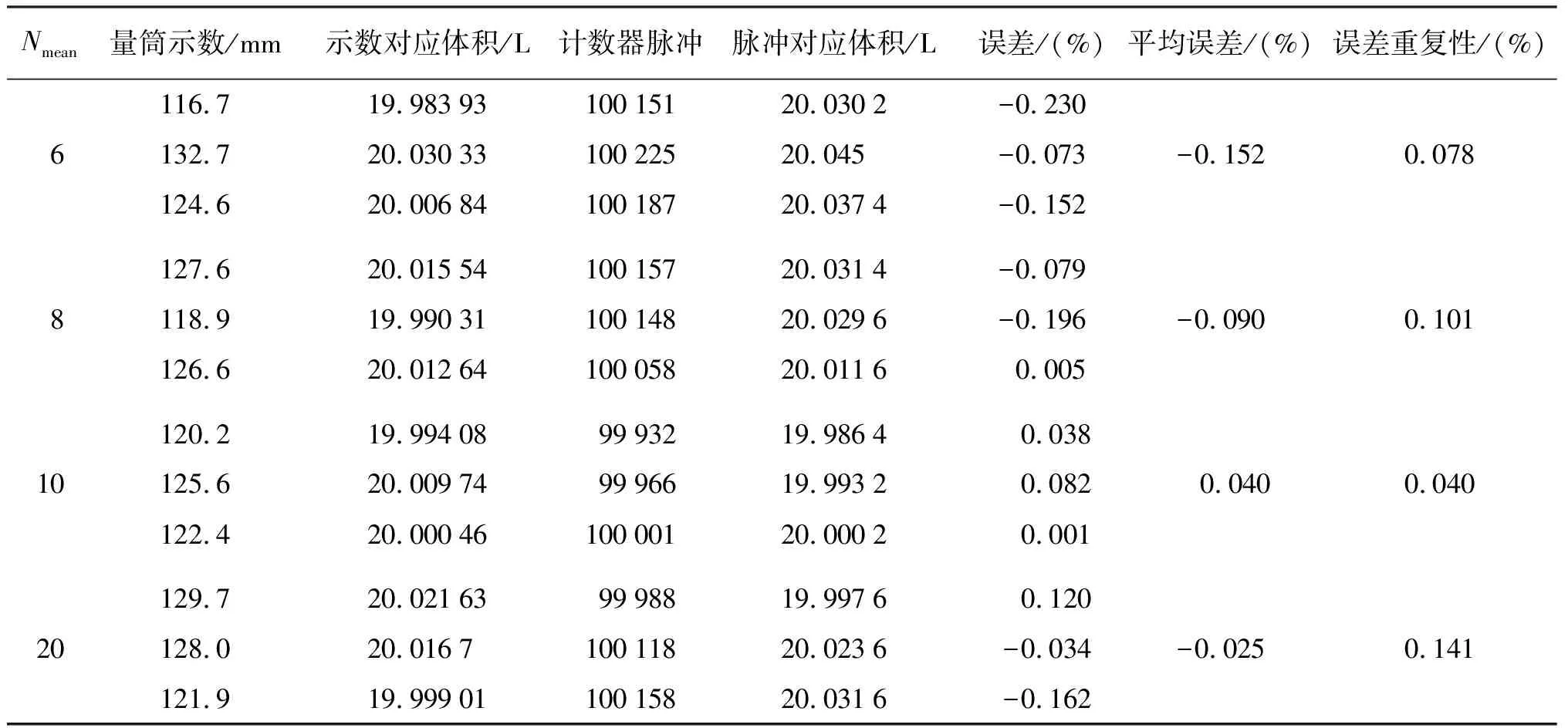
表2 大档位下的测量数据Tab.2 The experimental data of large flow
由表2可知,当Nmean=10时,测量具有较小的测量误差与较好的重复性。因此,取Nmean=10、采样频率为7 500 Hz,使用过零检测算法每采样500点调用一次算法更加适合尿素加注机的测量。
3.3 数字驱动方法
在驱动方式方面,传统的模拟驱动方法驱动信号依赖传感器信号、驱动增益控制不灵活,其有限的驱动增益和简单的增益控制算法致使其不能快速跟踪流量管的幅值变化和调整其相应的期望幅值,进而可能造成流量管停振,而且其缓慢的频率相位跟踪能力也不适用于流量快速频繁变化的场合。因此采用基于DDS和MDAC的数字驱动方法,结合非线性幅值控制算法,从而实现对流量管的驱动控制。由于加注开启过程流量急剧上升,加注结束阶段流量快速频繁变化,所以,需要驱动方式能快速跟踪传感器频率相位。全数字驱动频率跟踪性能强,当固有频率发生突变时,由于数字驱动是实时检测传感器输出信号的,因此,能通过频率估计算法算出当前的频率,从而给出相应的驱动信号。即使不能实时给出合适的驱动信号,也能判断出频率发生了较大变化,从而运用起始时的启振方法能快速使流量管再次进入新的稳定工作状态。因此,选用全数字驱动方式,既能满足实时性要求,也能保证较好的标定精度。
DSP实时采集传感器信号,得到信号的频率、相位信息后,通过数字接口将频率、初始相位信息写入到DDS(直接数字频率合成器)中,DDS即可输出所设定的频率、相位的正弦信号,作为驱动信号源。该信号接入到MDAC(乘法数模转换器)的模拟输入端。DSP得到传感器信号的幅值信息后,调用幅值控制算法,求得数字驱动增益,送至MDAC的数字输入端。MDAC将数字端与模拟端信号相乘经功率放大后即可输出包含幅值、频率、相位信息的驱动信号。其原理框图如图9所示。
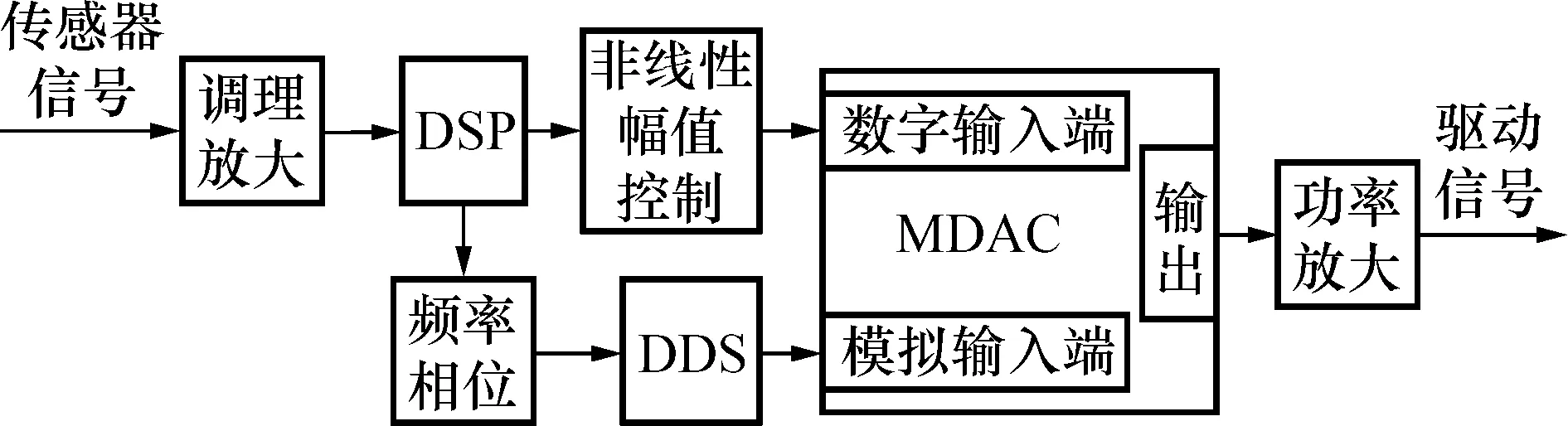
图9 数字驱动方法框图Fig.9 Block diagram of digital drive method
4 系统实现与实验验证
将改进后的算法在研制的基于DSP的科氏质量流量变送器上实时实现,匹配Endress+Hauser公司生产的DN25的F型科氏质量流量传感器,首先做了水流量标定试验,检测科氏质量流量计的测量精度;再做尿素加注机加注的标定试验,考核科氏质量流量计在尿素加注机中的动态响应速度和测量精度。
4.1 系统实现
4.1.1 系统硬件模块
以TMS320F28335为核心研制科氏质量流量变送器。TMS320F28335核心内包含有一个C28x定点CPU和一个浮点运算单元FPU,片上有McBSP、SPI、DMA、SCI、ePWM等丰富的外设资源,有利于实现仪表的各种功能,主要包括信号输入调理单元、数字驱动电路、DSP数字信号处理模块、人机接口及通讯电路以及温度补偿单元[13]。这可以实现传感器输出信号的采集与调理、驱动信号的合成与输出、流量的计算与显示等功能[14~15]。
4.1.2 系统软件模块
系统的软件设计采用模块化设计。即采用独立模块实现系统各个功能,并由主程序统一调用。软件结构框图如图10所示,主要包括主监控程序、初始化模块、中断模块、核心算法、人机接口、流量信号输出、通讯模块、FRAM以及看门狗等模块[16]。
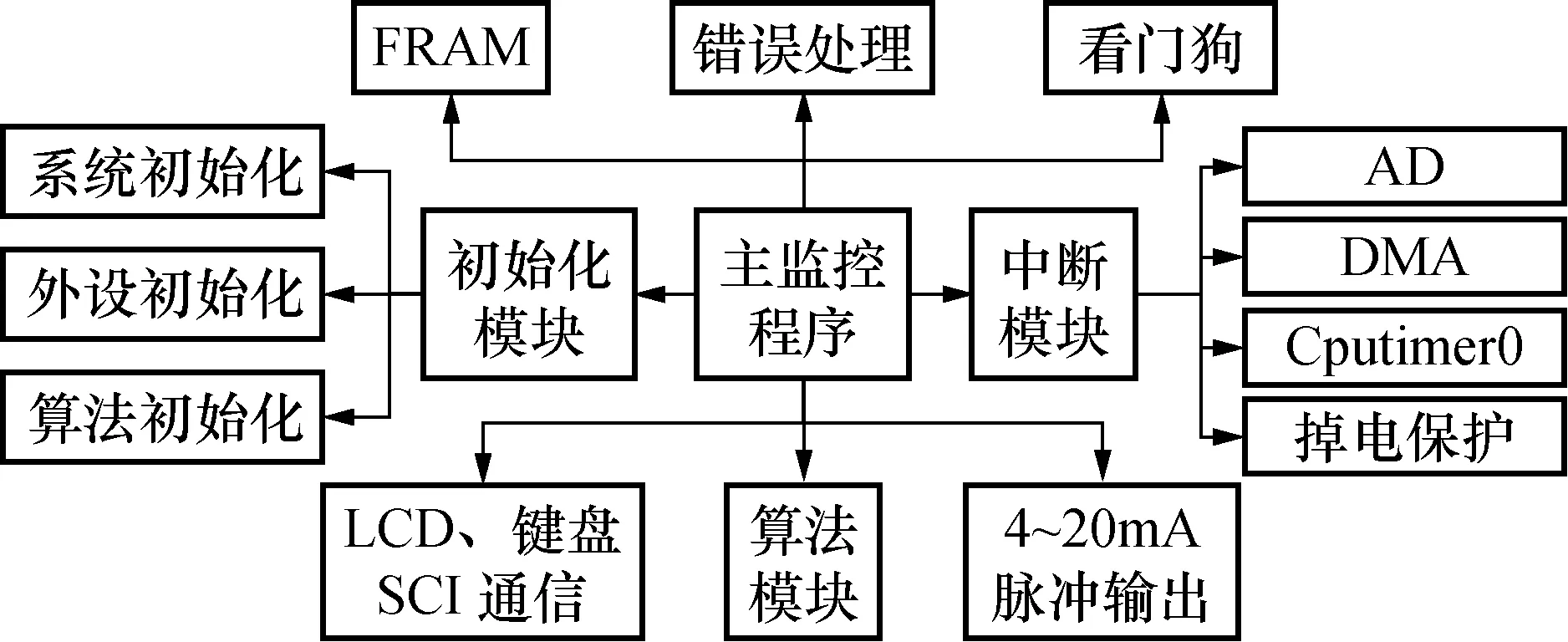
图10 系统软件框图Fig.10 Diagram of software for system
系统上电后,开始调用主程序:首先进行各模块、参数和算法的初始化;接着,同步开启两路A/D转换采样数据;然后,便调用算法计算流量,并进行温度补偿;最后,根据计算出的流量,发送PWM脉冲和4~20 mA电流。完成输出后,刷新液晶显示最新结果,并与上位机通讯,将结果显示在上位机界面上。最后返回,继续循环计算。系统的软件流程图如图11所示。
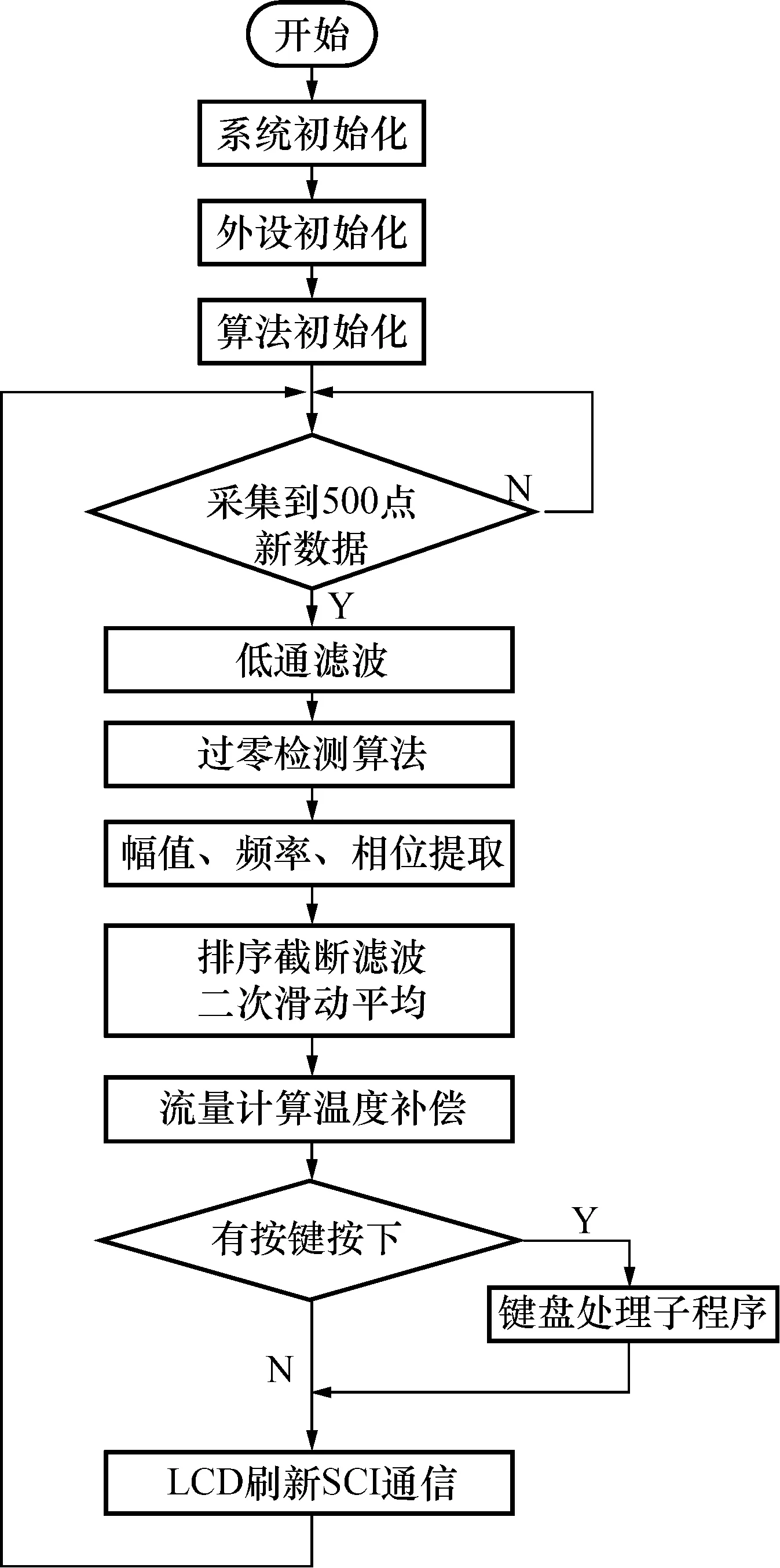
图11 系统软件流程图Fig.11 Flow chart of system software
4.2 水流量标定实验
采用称重法进行水流量标定实验。先在管道以最大流量冲水冲一段时间,消除水箱中的水与管道的温度差异而引起误差;然后将传感器管道两端堵住,将科氏质量流量传感器与科氏质量流量变送器连接好,上电,堵住传感器管道两端使传感器为满管零流量,运行程序一段时间,通过上位机GUI软件监测变送器计算出的相位差,不断清空直至零点较为稳定,测量1 000点,保存数据,平均该段数据的零点相位差,再通过GUI设入仪表参数的零点。零点修正后,开始标定,在显示的相位差较为稳定的情况下开始第一次标定。标定完最大流量点后,按照平均误差修改仪表系数。继续标定,若整个标定完后最大流量点发现误差仍较大,则按照最后一次最大流量点的平均误差再次修改仪表系数,重新标定,标定5个流量点(最大流量、最大流量的50%、20%、10%、最大流量)的标定结果。标定装置对脉冲的计数值乘以脉冲当量后作为测量值,电子秤的称重值作为流量的标准值,比较测量值和称重值即可得到科氏质量流量计的测量误差。实验装置如图12所示。该装置的不确定度水平为0.05%,符合国家对0.1级科氏质量流量计的检定标准。标定的结果如表3所示。
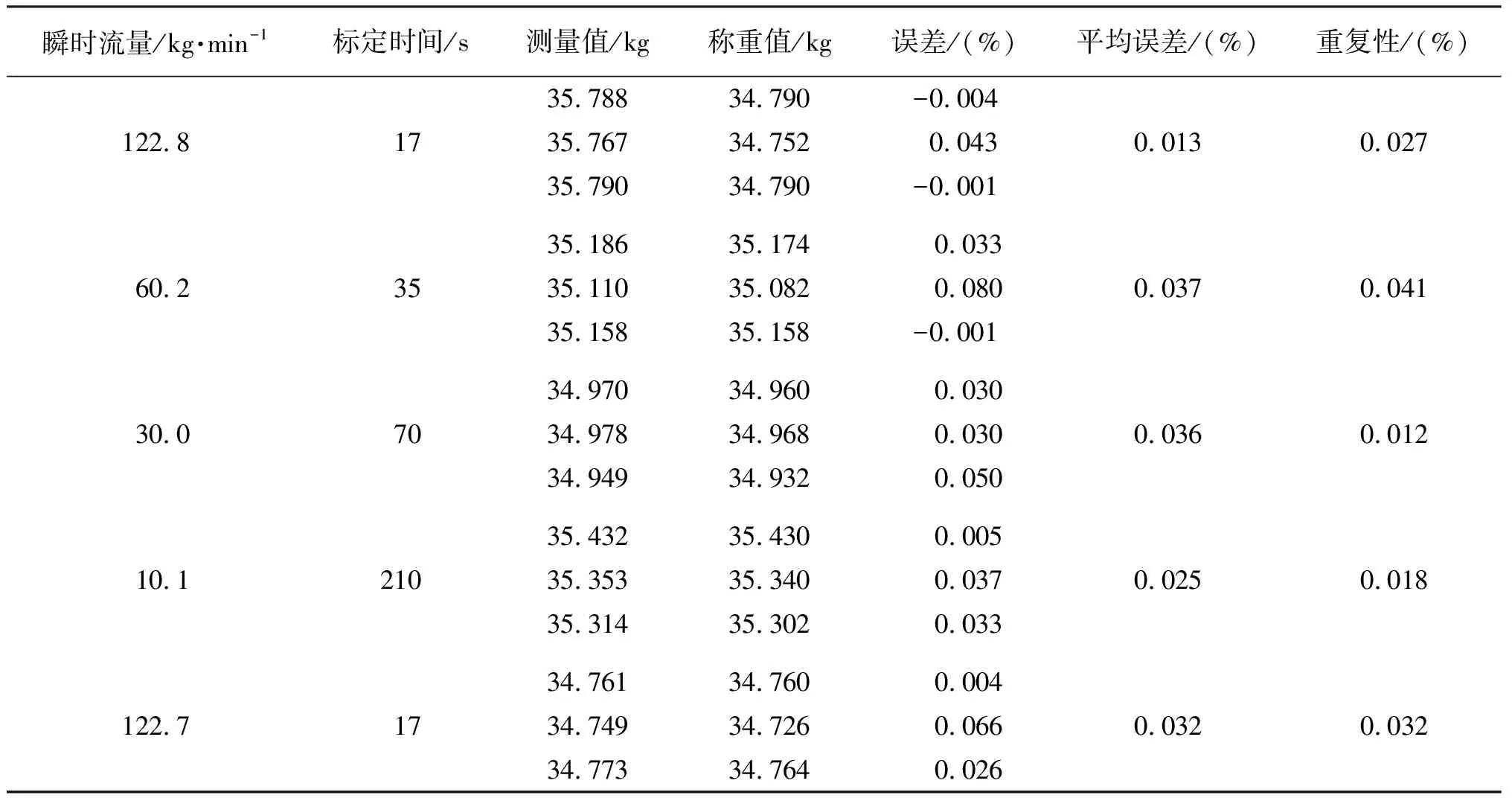
表3 水流量标定实验数据Tab.3 The water calibration experimental data
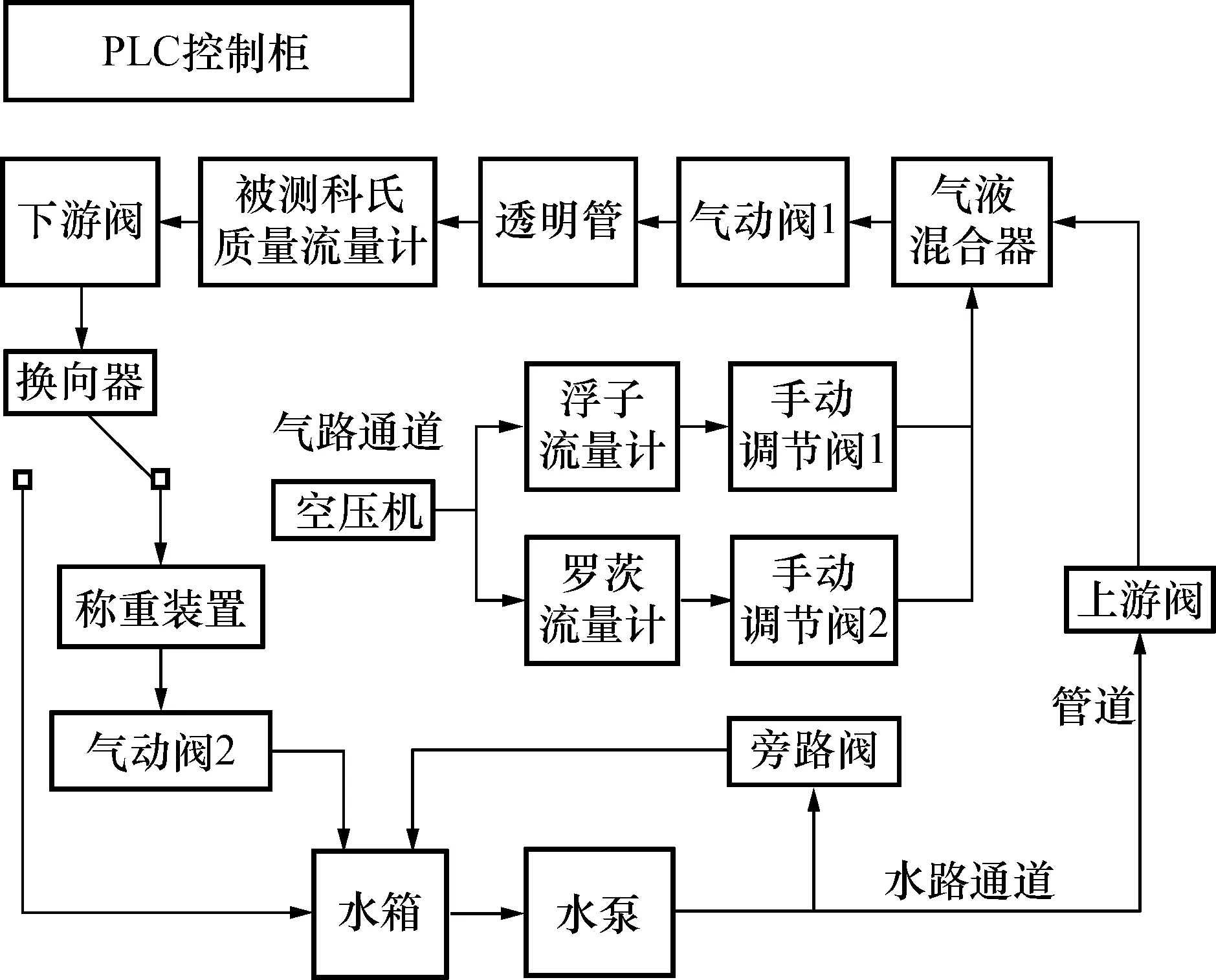
图12 水流量标定装置Fig.12 Calibration device schematic
由表3可知,在12:1量程范围内,该测试方案测量误差小于0.1%,重复性误差小于0.05%,满足0.1级精度要求。
4.3 尿素机测试实验
实验采用容积法标定,液体由尿素机水箱流出,经轻型立式多级离心泵抽水,先流经E+H公司生产的口径DN25型号为F的微弯型科氏质量流量传感器,再流经容积式流量计,用以检测是否达到预定加注升数,该表测量的最大允许误差为±0.2%,最后经水枪流入标准金属量器中。
该量器是由河北海兴东方计量仪器有限公司生产的BJL型号,容量20升,测量精度0.025%,符合国家对0.1级科氏质量流量计的检定标准。测量过程使用脉冲计数,计数设备为美国芬兰贝美克斯Beamex MC2多功能校验仪。现场尿素加注装置如图13所示。
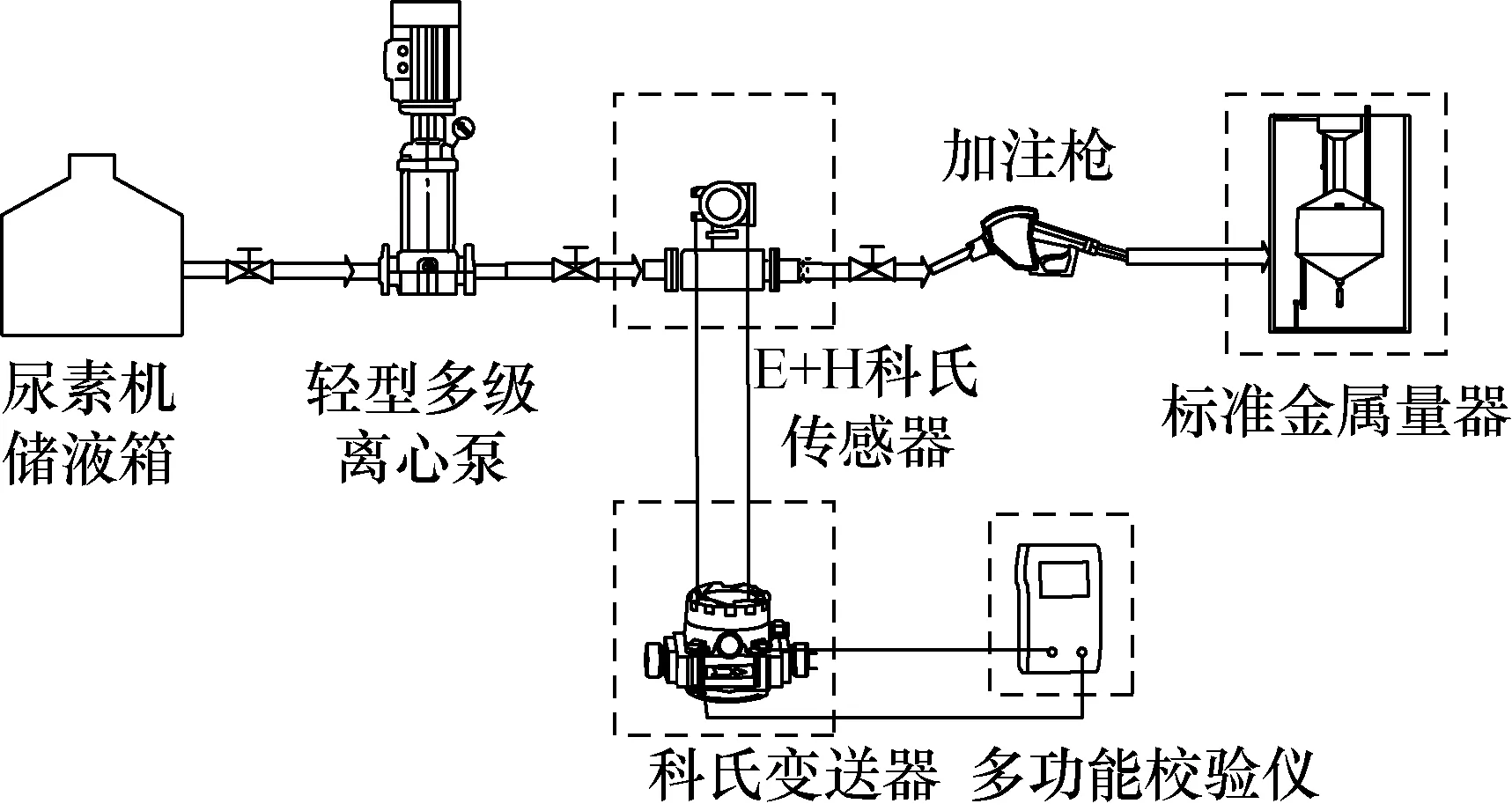
图13 现场尿素加注装置Fig.13 The urea filling equipments
加注具体步骤如下:
1) 在尿素加注机仪表盘上设置好加注升数(20 L),提枪。
2) 将水枪口放入标准金属量器中,打开水枪,按至预定挡位,向标准金属量器中加水。
3) 加注人员检测加注机上显示的已加注升数,至17 L时,主动减小流量,以免末尾阶段冲击过大液体溅出,导致标定误差。
4) 加注至接近20 L时,由机器自动控制以最小流量流入,直至加注机仪表上显示已加注至20 L。记录标准金属量器的示数,根据厂商给出的公式换算成对应的升数;变送器实时测量流体流量值,并采用脉冲输出的方式,将脉冲数上传到Beamex MC2多功能校验仪中。标定装置对脉冲的计数值乘以脉冲当量后作为测量值,标准金属量器的换算值作为流量的标准值。
5) 重复以上步骤3次,考察被检表的重复性。改变档位(最大流量),重复上述步骤。
由表4可知可见,算法改进后,被检表测量精度优于0.1%,重复性误差小于0.05%,满足0.1级精度要求。因此,改进后的算法与系统具有较高的精度与性能。
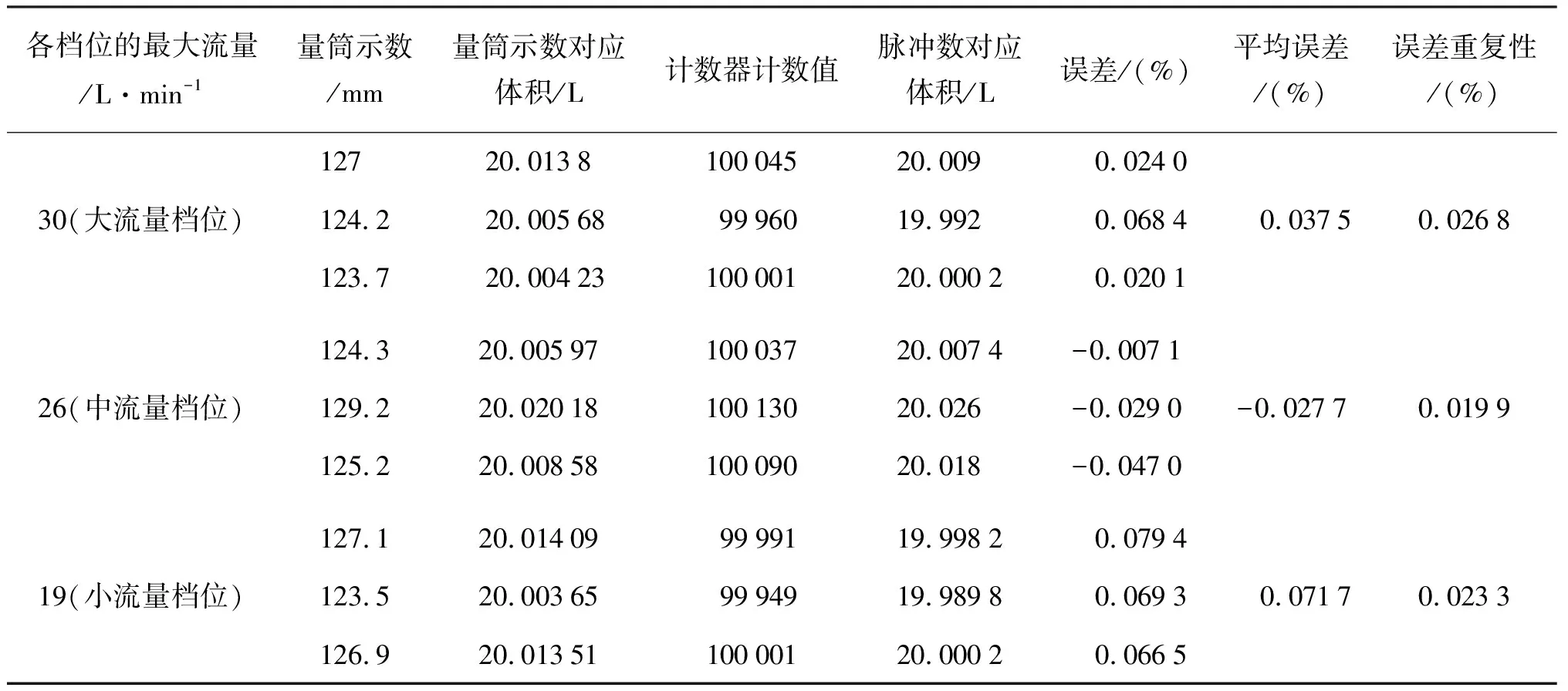
表4 滑动平均数组长度设为10的实验结果Tab.4 Experiment results with setting the average sliding array length to 10
5 结 论
为了将微弯型高频传感器的科氏质量流量计应用在尿素加注机上,根据实际尿素加注过程采集了传感器输出的原始信号,使用MATLAB编写过零检测算法,计算出尿素机从开启到停止的加注过程3个流速档位的相位差随时间变化过程,并建立了模型,较好地描述实际加注过程的信号相位差变化;说明各流速的相位差模型开启阶段均为斜坡函数,平稳加注阶段均为常数的形式,能够较好地描述实际加注过程中传感器信号相位差的变化。
基于加注过程的相位差变化可以看出,由于选用的微弯型传感器固有频率非常高、相位差非常小以及流量频繁变化,这就对尿素机加注过程中的动态响应速度、小流量的测量精度都提出了较高的要求。分析了工业领域应用较为广泛的、实际应用效果较好的DTFT算法与过零检测算法的优缺点,得出仅过零检测算法既能满足采样精度,又能保持较高的动态响应速度的结论;分析了滑动平均数组长度对算法的响应速度的影响。进行不同挡位下的加注测试以评估出最合适的滑动平均数组Nmean,最后得出滑动平均数组设为10时,既能满足实时性要求,又能保持较好的测量精度;分析选用了全数字驱动方法进行驱动,适用于尿素机加注场合。
改进的数字信号处理算法在以TMS320F28335为核心的科氏质量流量变送器上实时实现,并进行了水流量标定和尿素机加注标定实验。实验结果表明:算法改进后,在水流量标定实验中,12:1的量程范围内,测量误差小于0.1%,重复性误差小于0.05%,性能优良;在尿素加注标定实验中,测量误差小于0.1%,被检表重复性误差小于0.05%,达到0.1级测量精度,具有较高的精度与优良的性能。
