逆向工程中圆锥体组件加工信息快速高精度检测与生成方法研究
2022-07-21孔德明田小强崔永强孔令富
孔德明, 田小强, 崔永强, 孔令富
(1.燕山大学 电气工程学院,河北 秦皇岛 066004; 2.燕山大学 信息科学与工程学院,河北 秦皇岛 066004; 3.根特大学 通信与信息处理系,比利时 根特 B-9000)
1 引 言
圆锥体或部分圆锥体构成的机械零部件在船舶、汽车乃至航空、航天领域有着广泛的应用[1,2]。这些机械零部件往往是通过逆向工程制造方法生成产品的制造加工信息,其信息精度的高低将直接影响到产品的使用质量与寿命,如何快速高精度实现对圆锥体组件加工信息的检测与生成,是当前机械零部件逆向加工中,特别是在3D制造技术逐渐成熟发展的情况下,急需认真解决的重要问题。
目前圆锥体组件加工信息检测与生成方法主要采用直接接触测量法,包括游标卡尺测量、角度样板检测、正弦规测量等[3,4]。这些传统测量方法在实际测量过程中,由于各种原因往往会引发被测圆锥体组件产生弹性形变,从而引入测量误差;或者由圆锥体构成的部分在装配整合时,往往可能嵌入整体机械零部件的里内部,这就限制了一些传统测量工具对该部分的圆锥体进行测量以生成必要的机械制造加工信息;且这些方法耗时较长,已很难满足实际生产检测过程中日益提高的测量需求。非接触测量方法主要包括光视觉测量、摄影测量、三维光学扫描仪、激光跟踪仪等。在快速高精度测量领域,经常通过使用三维光学扫描仪获取机械零部件表面的空间点的位置信息,即点云数据;然后,再使用点云数据处理技术提取出机械零部件表面的几何信息。由此可见,点云数据处理是机械零部件逆向工程加工中的一项重要技术环节[5,6]。
本文采用三维光学扫描仪,在直接获取机械零部件表面的空点点云数据的基础上,提出了一种圆锥体组件加工信息检测与生成方法。该方法对圆锥体组件点云数据进行处理,获取其三角网格(triangulated irregular network,TIN)模型及最近邻域平面法向量;再根据空间点与法向量二者之间的映射关系以及圆锥体组件在三维空间内的整体形貌,快速而高精度地获取到圆锥体组件的整体加工信息。
2 圆锥体组件加工信息检测过程
2.1 映射关系的建立
在点云数据TIN模型的基础上,建立圆锥体点云数据中各空间点与其法向量之间的映射关系[7,8]。首先,采用Delaunay网格划分法对点云数据进行处理得到TIN模型;然后,根据点云数据的TIN模型,得出点云数据内各空间点的最近邻域;最后,利用最小二乘拟合方法对最近邻域点集内的各个点进行计算,获取其最近邻域平面[9,10],进而得到该点最近邻域平面的法向量。法向量的方向指向圆锥体的外侧,根据法向量及其方向,在三维空间内建立法向量空间坐标系NVxOy,如图1所示。

图1 i点最近邻域平面的法向量图Fig.1 Normal vector of fitting plane of nearest neighborhood of point i
图1中:θ为锥角;h为锥高;r为圆锥体底面圆半径;i为圆锥体表面任意一点;K为圆锥体的顶点;O为底面圆的中心点;G为直线Ki与底面圆之间的交点;k1为直线KG的斜率;k2为直线in的斜率;α为直线KG与直线OG之间的夹角;β为法向量与法向量平面NVxOy之间的夹角。
α与β之间的关系如式(1)~式(4)。
(1)
(2)
(3)
k1·k2=-1
(4)
圆锥体的方程如下式:
(5)
式中:a、c为任意不为零的常数,式(5)两边对r求导数为
(6)
将式(2)和(4)代入(6)得到:
(7)
圆锥体的法向量为
(8)
将式(7)代入式(8)得到:
(9)
(10)

在实际测量过程中,由于测量的不确定性和点云数据中点的离散分布,被测圆锥体点云数据中大多数点的法向量分布在一圆环带内而不是圆环上。使用算术平均滤波方法对点云数据的法向量进行滤波[11]。
为了得到滤波后的法向量的分布规律,利用多项式拟合方法[12,13]中的平面拟合得到滤波后的圆环带与NVxOy之间的距离D如式(11)。然后根据多项式拟合中的曲面拟合得到滤波后的圆环带的表达式(12)。将式(11)代入式(12)便得到圆环带的半径R。
D=nvz=fp
(11)
(12)
(13)
2.2 圆锥体组件加工信息的检测与生成
根据圆锥体点云数据法向量分布圆环带的半径R与距离D之间的比值关系:
(14)
将式(1)、(2)、(6)、(11)和(10)代入公式(14)得到:
(15)
根据式(15)计算出圆锥体的锥角:
(16)
选取圆锥体点云数据中Z坐标值最大的点P,该点的Z坐标值作为圆锥体的锥高。

(17)
将圆锥体的锥角θ和锥高h代入式(2),得到圆锥体底面圆的半径r。
(18)
通过本文方法在求得θ、h和r这些基本加工信息后,即可得到被测圆锥体组件所有加工信息。
3 仿真研究
图2为某一型号航空发动机结构示意图,其叶片上的一部分由圆锥体构成[14,15],该部分位于发动机的排气口处。由于该部分圆锥体嵌入机械零部件的里内部,对其加工信息进行检测与生成时,可采用非接触式测量方法对其进行快速高精度检测。由于三维扫描仪可以深入到机械零部件内里部对叶片上由圆锥体构成部分进行高精度扫描,其具体测量系统示意图如图2排气口处所示,高精度扫描将直接获取到被测体的点云数据。因此,可采用本文方法对航空发动机叶片部分的圆锥体加工信息进行检测与生成。具体的仿真研究过程如下:选取仿真模型1(锥角为96.026°,锥高为45 mm,底面圆半径为 50 mm);仿真模型2(锥角为30.000°,锥高为186.603 mm,底面圆半径为50.000 mm);仿真模型3(锥角为60.000°,锥高为77.941 mm,底面圆半径为45.000 mm)等6个圆锥体模型作为航空发动机叶片上圆锥体仿真研究对象,但为了简化其处理过程,文中仅给出仿真模型1的点云数据图,如图3所示。

图2 航空发动机的结构示意图Fig.2 Structure schematic of an aeroengine

图3 仿真模型1点云数据图Fig.3 Point cloud of simulation model 1
采用Delaunay网格划分方法对点云数据进行处理获取TIN模型,然后计算点云数据内各空间点的最近邻域平面法向量。根据算术平均滤波方法对法向量进行滤波处理,其结果分布如图4所示。

图4 法向量滤波结果图Fig.4 Result of normal vector filtering
利用多项式拟合方法对滤波后法向量的分布点进行多项式拟合,其中多项式平面拟合如图5所示,多项式曲面拟合如图6所示。

图6 法向量的多项式曲面拟合结果图Fig.6 Fitting result of polynomial curve fitting
根据图5所示的多项式平面拟合结果得到点云数据法向量与NVxOy之间的距离D,通过图6所示的多项式曲面拟合结果以及式(11)、式(12)和式(13)得到圆环带的半径R。将D和R代入公式(16)得到θ。在点云数据中选取Z坐标值最大的点P(62.826,54.974,44.998),根据式(17)得到h。将θ和h代入式(18)得到底面圆的半径r。
目前,在形状检测领域,几何测量是一种常用的较好检测方法[16,17],该方法根据圆锥体方程与不同类型二次曲面模型几何关系,得到圆锥体的具体加工信息,由于在检测过程中对二次曲面模型方程参数进行优化,使用几何测量方法能够得到更好的检测结果。
为了验证本文方法的稳定性和快速准确性,分别选择本文和几何测量两种方法对6个仿真模型加工信息进行检测与生成,两种方法的加工信息生成结果和运行时间t如表1所示。

表1 两种方法的加工信息生成结果和运行时间表Tab.1 Results of generated machining information and time consuming
为了更加直观圆锥体组件加工信息生成过程的精度,现给出6个仿真模型的加工信息标准值如表2所示。
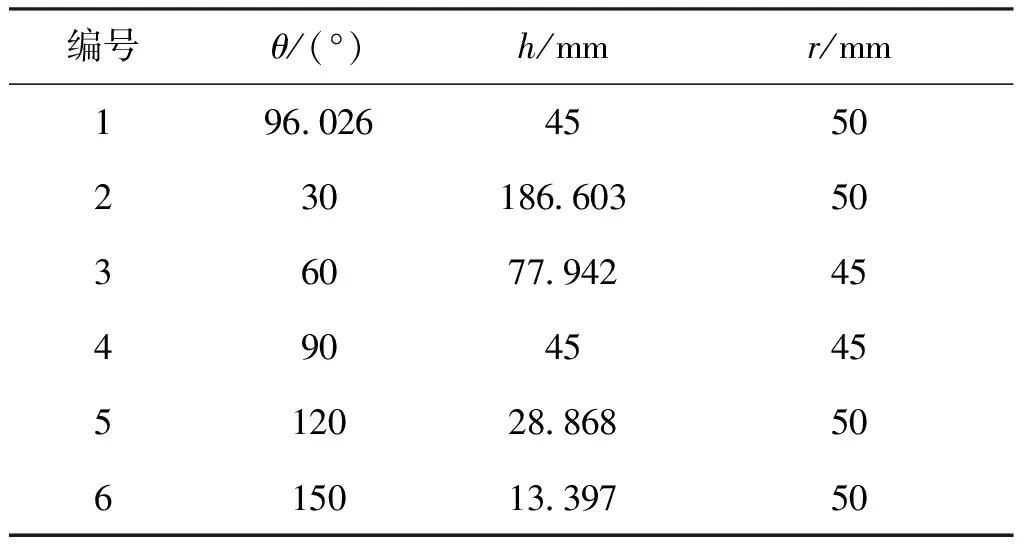
表2 6个仿真模型的加工信息标准值表Tab.2 Standard values of six simulation models machining information
两种方法所对应的6个仿真模型加工信息生成过程产生的锥角误差Δθ、锥高误差Δh、底面圆半径Δr和时间t如图7所示。

图7 两种方法加工信息生成过程误差分布图Fig.7 Error distribution of generated machining information by using two methods
对比两种方法对6个仿真圆锥体组件加工信息过程误差结果,能够得到本文方法圆锥体组件的θ、h和r的误差分别降低了77.64%、70.53%和73.48%,时间t缩短了81.74%,说明本文方法能够实现对圆锥体组件加工信息的快速高精度检测与生成。
4 结 论
本文提出了一种圆锥体组件快速高精度加工信息检测与生成的一种新方法。选用本文方法和几何测量方法分别对6个仿真圆锥体模型的加工信息进行检测与生成,其生成加工信息结果表明本文方法圆锥体组件的锥角θ、锥高h和底面圆半径r的误差分别降低了77.64%、70.53%和73.48%,时间t减少了81.74%,对后续的圆锥体组件在线检测和加工信息的生成具有很好的参考价值和借鉴意义。
