基于可变形卷积的双目视觉三维重建

李鹤喜， 李威龙

(五邑大学 智能制造学部,广东 江门 529020)

1 引 言

基于双目视觉的三维重建技术是立体视觉的一种重要实现方式[1]，是通过双目相机拍摄的图像进行立体匹配获取视差信息，最后恢复出三维形状。

立体匹配是双目视觉三维重建的关键技术[2]，是从获取的同一场景的两幅图像中，寻找重叠区域的匹配对应点，进而得到视差图。传统的立体匹配一般分为4个步骤[3]：计算像素对应点的匹配代价并构建代价空间、代价聚合、视差估计和优化。Hischmiller H[4]提出了半全局立体匹配算法(SGM)，该方法使用了互相关信息作为匹配代价，较好地实现了在精度和速度上的平衡；但是由于采用手工设计的特征进行匹配，在精度方面仍然难以达到令人满意的效果。Zbontar J等[5]提出了一种基于深度学习的立体匹配MC-CNN算法，此后，相关学者对基于深度学习的立体匹配算法[6～11]做了大量研究。现有的基于深度学习的立体匹配算法大致可以分为两大类：视差直接回归方法和基于匹配代价空间方法。视差直接回归方法不考虑立体几何约束[12]直接从输入的图像对中恢复视差，如：文献[6]中的DispNetC算法采用一种U型编码器-解码器结构来回归视差；基于匹配代价空间方法通过视差偏移来构建3维代价空间或4维代价空间，文献[8]中的GC-Net算法通过聚合操作来构建4维代价空间。从视差图中恢复场景的深度信息在自动驾驶，增强现实，机器人导航等方面应用广泛，而这些应用大多数都要求立体匹配的实时性。现有的基于深度学习的立体匹配在精度方面表现越优，大多数模型的参数量就越大，难以达到实时的要求，GC-Net算法在构建匹配代价空间时采用聚合操作，这就使得算法的规模增加，参数量达到3.5×106；AutoDispNet算法采用神经网络结构搜索技术，其中学习编码器-解码器采用了较多的网络架构单元，使得网络的参数量更是达到1.11×108。

针对上述问题，本文提出一种基于可变形卷积的立体匹配算法。首先,采用二维可变形卷积对输入的左右“图像对”提取更加有效的特征；然后，利用三维可变形卷积在匹配代价空间中有效地聚合两图像之间的相关性；最后，以级联残差学习方式构建的3个阶段，来有效地解决匹配代价空间所带来的计算参数量大的问题，达到立体匹配实时的要求。

本文将从双目相机标定、立体校正、立体匹配和三维物体重建这4个完整的立体视觉工作流程，来叙述所提出算法的基本原理和实现效果。

2 双目相机标定与立体校正原理

2.1 双目相机标定

相机标定的目的就是建立相机图像像素位置与物体空间位置之间的关系，即图像坐标系与世界坐标系之间的关系。主要是求解相机的内外参数和畸变参数。

在不考虑相机畸变参数的情况下，假定已知像素坐标系和世界坐标系的齐次坐标映射关系如下：

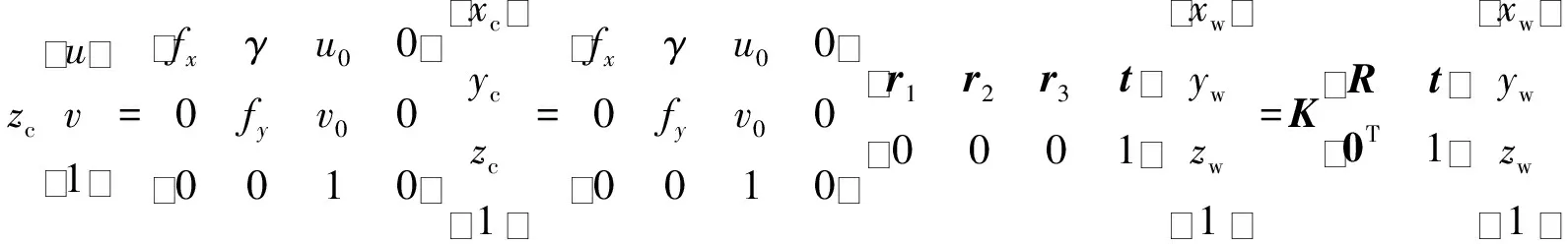
(1)

式中：(u,v)表示像素坐标点；K表示相机内参矩阵；fx=f×sx，fy=f×sy，其中，f表示物理焦距，sx和sy分别为x和y方向上的1 mm长度所代表像素；(u0,v0)表示像素坐标原点；γ表示制造误差产生的两个坐标轴偏斜参数，通常可以忽略；R=[r1,r2,r3]，表示旋转矩阵；r1,r2,r3分别表示旋转矩阵每1列的向量；t表示平移向量，代表相机外参；(xc,yc,zc)表示相机坐标点，(xw,yw,zw)表示世界坐标点。

采用单平面棋盘格进行标定，可以假定棋盘位于世界坐标zw=0的位置，式(1)可简化为

(2)

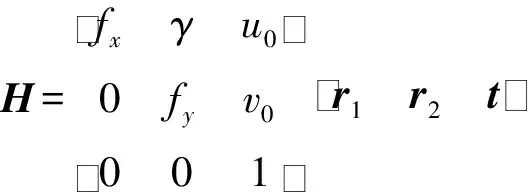
(3)

式中：xij表示棋盘角点在像素坐标下的实际值,n、m分别表示所选取的角点在不同平面上的成像点总分数和对应的空间点总数；x′表示估计值；三维空间点Pj(xw,yw,zw)经过初始的R，t，K变换得到x′。

由相机透镜形状引起的畸变称为径向畸变；而在相机组装过程中，如果透镜与成像平面不平行，就会引入切向畸变。对于畸变，可用以下函数进行矫正。

径向畸变矫正函数：

(4)

式中：(xd,yd)表示畸变后的图像坐标点；(x=xc/zc,y=yc/zc)表示理想坐标点；(k1,k2,k3)表示径向畸变参数；r2=x2+y2。

切向畸变矫正函数:

(5)

式中p1和p2表示切向畸变参数。

考虑到透镜畸变的影响，可将畸变参数一起放到优化函数中，式(3)变为

(6)

上述为单目标定，双目标定就是分别对左右相机进行单目标定，得到左右相机的内外参数，畸变系数，然后确定左右相机坐标系之间的相对关系：

(7)

式中：旋转矩阵R′和平移向量t′表示左相机到右相机的坐标转换；Rl和tl表示左相机外参，Rr和tr表示右相机外参。

2.2 立体校正

立体校正前后模型图如图1所示，即在立体匹配之前，利用双目相机标定的内参以及左右相机坐标系之间的相对关系，把消除畸变后的两幅图像的极线对齐。

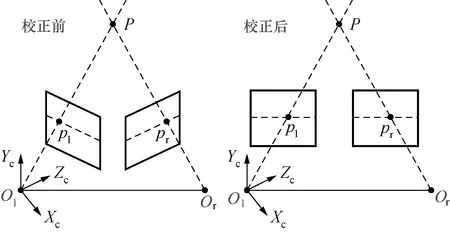
图1 立体校正Fig.1 Stereo rectification

3 立体匹配算法

基于可变形卷积的立体匹配算法由特征提取、匹配代价空间、代价后处理、视差/残差回归与视差优化模块组成，立体匹配算法设计如图2所示。

特征提取模块是一个在编码阶段引入2维可变形卷积沙漏型的编码器-解码器；匹配代价空间的构建采用DispNetC的相关联操作来形成3维代价空间；代价后处理模块采用残差结构的3维可变形卷积对匹配代价空间进行正则化处理；视差回归模块采用GC-Net所提出的soft argmin方法，表达如下：

(8)

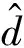
视差优化模块为空间传播网络(spatial propagation networks)[14]，该网络能提取图像的相似度矩阵，对预测的视差值进行指导优化。

算法分3个阶段得到不同精度的视差图。

在第1阶段，特征提取模块提取出分辨率为1/16的特征图F1，因此,候选的视差值范围变成0～1/16Dmax，所以在视差回归与优化后，需要通过上采样操作和乘以16倍来得到第1阶段的视差图；

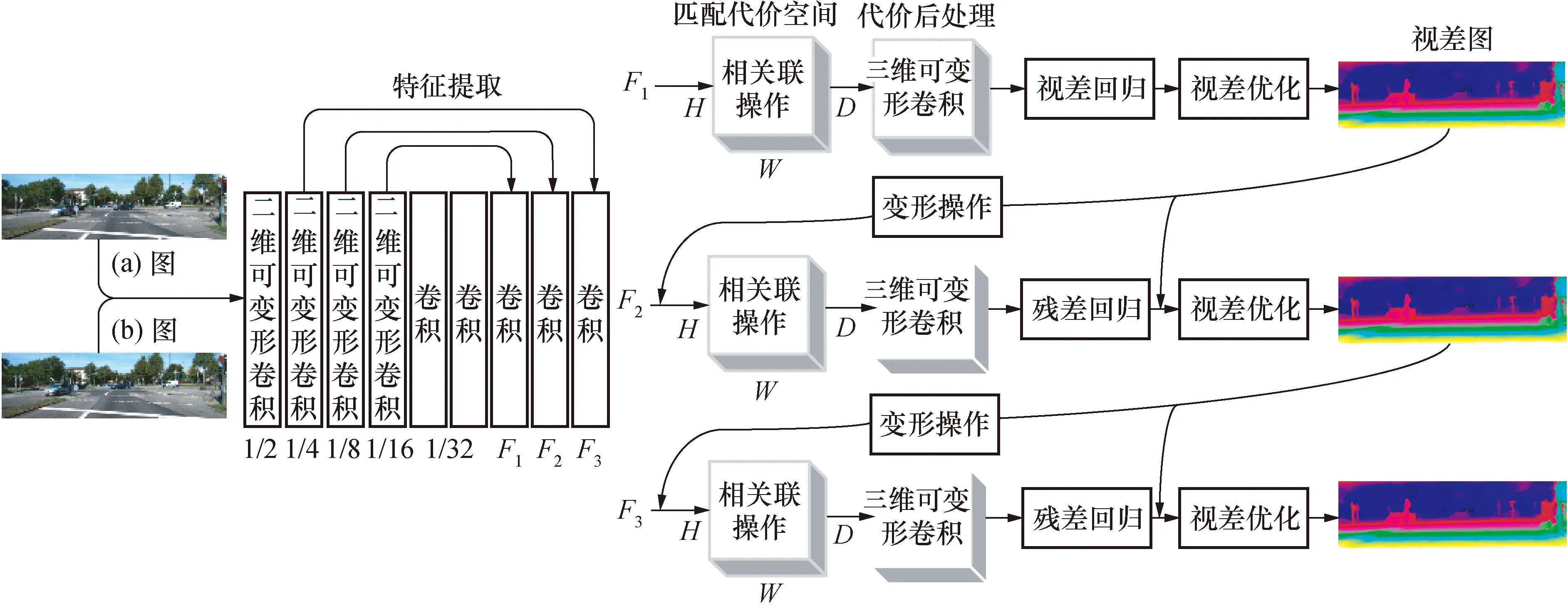
图2 立体匹配算法设计Fig.2 Design of stereo matching algorithm

在第2阶段，将候选的残差值d的范围设置为-2～2，根据第1阶段的视差图在分辨率为1/8的右特征图F2进行变形(warp)操作形成新的特征图，然后与左特征图形成匹配代价空间，回归的残差图添加到第1阶段的视差图，再对视差图进行优化，得到第2阶段的视差图；第3阶段与第2阶段同理进行。

3.1 可变形卷积

普通的卷积由两个步骤组成：1) 在输入特征图x上使用一个规则的网格R进行采样；2) 采样值乘以权值w再进行求和。例如，R={(-1,-1),(-1,0),…,(0,1),(1,1)}表示一个扩张率为1的 3×3的网格，对于在输出特征图y上的每个位置p0，有：

(9)

式中：pn表示属于R的每一个位置。

在可变形卷积中，R加入了偏移值{Δpn|n=1,…,N=|R|}，式(9)变成：

(10)

现在，采样是在规则和偏移的位置上进行pn+Δpn，因为Δpn为小数，式(10)需要通过线性插值来实现，有：

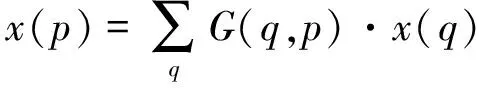
(11)

式中：p表示任意的位置，在式(10)中p=p0+pn+Δpn；q表示特征图x的每一个整数位置，G(*)有两个维度，可以分为两个一维核：

G(q,p)=g(qx,px)·g(qy,py)

(12)

式中：g(qx,px)=max(0,1-|qx-px|)。

图3为卷积核大小为3×3的二维可变形卷积。其偏移值是通过在同一个特征图上添加一层卷积获得，其卷积核的大小和扩张率与当前可变形卷积核一样。2N表示卷积的通道数，对应N个二维偏移值。三维可变形卷积是二维可变形卷积的推广，卷积的维度增加一维，其原理相同。

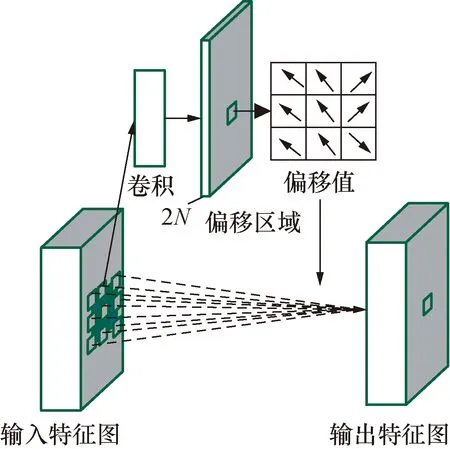
图3 3×3 二维可变形卷积Fig.3 3×3 2D deformable convolution

3.2 空间传播网络

空间传播网络结构如图4所示，用于优化回归的视差图。主要包含一个可微分的线性传播模块和一个学习相似度矩阵的深度卷积神经网络模块。空间传播网络的线性传播是在4个固定的方向：左到右，上到下和反向，对矩阵逐行或列进行扫描。下面主要介绍从左到右方向，其它方向原理相同。

图4 空间传播网络Fig.4 Space propagation network

首先，假设两个大小都为n×n的二维图像X和H，其中X为空间传播前图像，H为空间传播后图像，大小为n×1的xt和ht分别为它们各自的第t列。通过使用n×n线性变换矩阵Wt在相邻两列从左到右进行线性传播，

ht=(I-Dt)xt+Wtht-1,t∈[2,n]

(13)

式中：I表示n×n单位矩阵；初始条件为h1=x1；Dt(i,i)为对角矩阵，第i个元素为Wt第i行的求和。

(14)

因此，矩阵H(ht∈H,t∈[1,n])是按列以递归的方式进行更新，对于每一列，ht为其前一列ht-1乘以矩阵Wt并与xt结合产生，是线性的。当递归完成时，式(13)的矩阵表达如下：

(15)

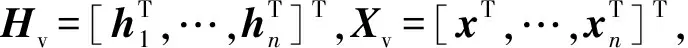
深度卷积神经网络模块主要是用来输出相似性矩阵G，然后进行线性传播得到Hv。算法主要用深度卷积神经网络和线性传播模块从左图像中学习H，来指导优化回归的视差图。

3.3 损失函数

损失函数主要采用平滑的L1损失与L2损失相比，平滑的L1更加鲁棒和对异常值敏感性更低，定义如下：

(16)

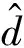
(17)

4 实验结果与分析

4.1 相机的标定与立体校正

采用7×10的棋盘格对双目相机进行标定，每个格子20 mm。双目相机保持不动，不断改变棋盘的位置采集25组图片来进行标定。图5为棋盘角点提取示意图。

图5 棋盘角点提取Fig.5 Checkerboard corner extraction

标定参数结果如表1所示。

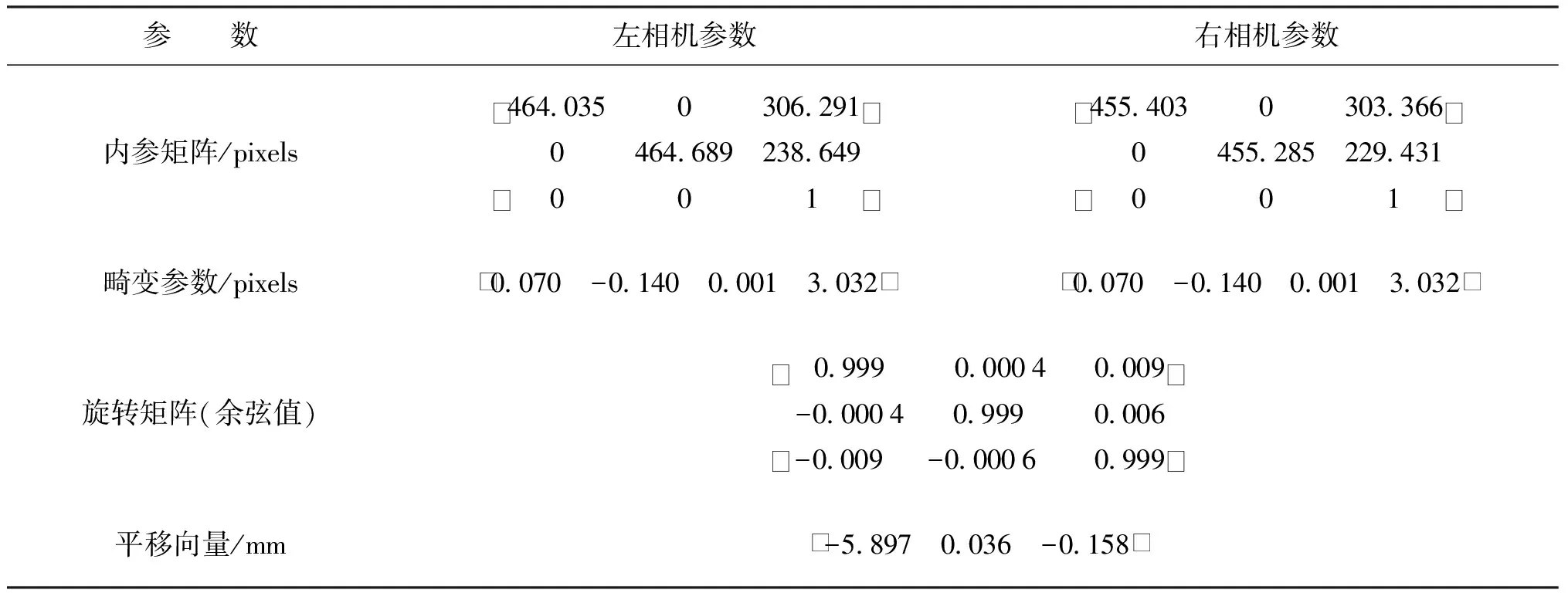
表1 左右相机标定参数结果Tab.1 Results of left and right camera calibration parameters

立体校正采用Bouguet[15]校正算法，立体校正结果如图6所示。

图6 立体校正结果Fig.6 Resul of stereo rectification

4.2 立体匹配模型的验证

首先对基于可变形卷积的立体匹配算法在SceneFlow[6]、KITTI2015[16]数据集上进行验证，并和传统算法进行比较。

数据集：SceneFlow是一个大规模合成的数据集，包含35454张训练图像对以及4370张测试图像对，分辨率为540×960 pixels，且提供了稠密的视差图；KITTI2015包括200张训练图像对以及200张测试图像对，记录了不同天气条件下的真实场景，分辨率为 1 240×376 pixels，提供了由激光雷达获取的稀疏视差图。

评价指标：对于SceneFlow数据集采用端点误差(end-point-error，EPE)作为评价指标，即预测视差值与视差真值的平均欧氏距离；对于KITTI2015数据集采用3像素误差(3-pixel-error，3PE)作为评价指标，即图像中误差大于3像素的点所占总像素点的百分比。

立体匹配算法网络如表4所示，所有卷积操作无偏置，后带有批标准化(batch normalization)和ReLU激活函数。

立体匹配算法实验均在Ubuntu16.04上进行，训练和测试使用1块GPU显卡，型号为NVIDIA GeForce GTX2080Ti显卡，采用的深度学习框架为pytorch1.2.0，优化器选择Adam，参数设定:β1=0.9，β2=0.99，最大视差设为192。

图7为算法在KITTI2015数据集上的测试结果，每个阶段的3像素误差(3PE)以及运行时间如表2所示。表3为在SceneFlow数据集上3个阶段的端点误差(EPE)测试结果。

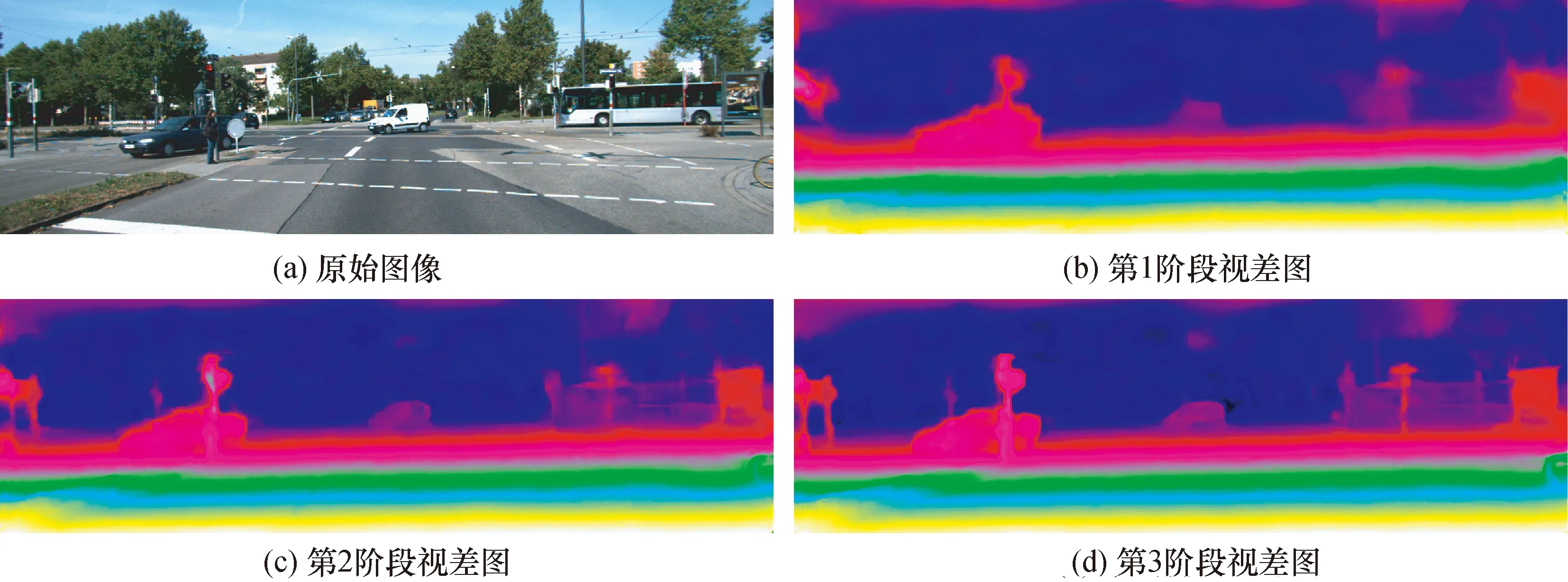
图7 KITTI2015数据集上的测试结果Fig.7 KITTI2015 dataset test results

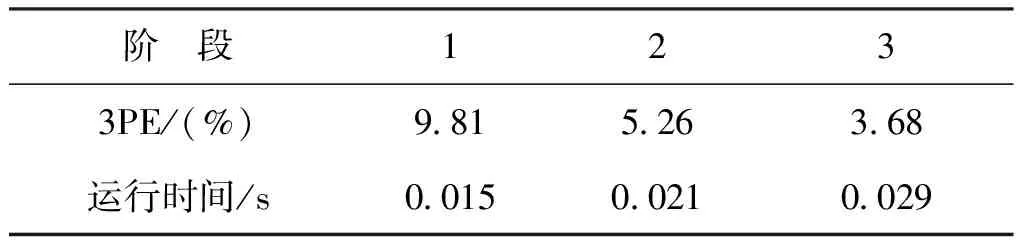
表2 在KITTI2015数据集的3个阶段测试结果Tab.2 Three-stage test results on the KITTI2015 dataset

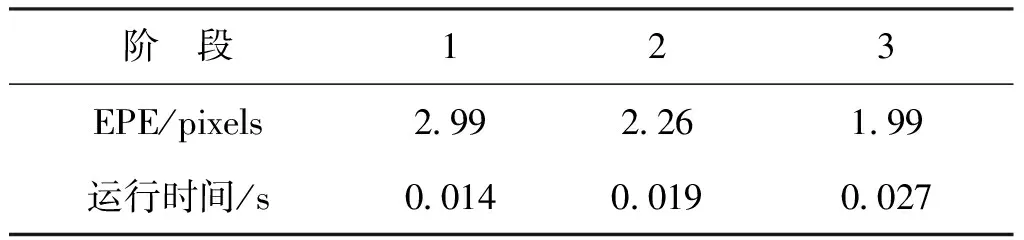
表3 在SceneFlow数据集的3个阶段测试结果Tab.3 Three-stage test results on the SceneFlow dataset

从图7、表2、表3中可看出，一个阶段比一个阶段的视差精度高，而且运行时间只是略微增加，该算法可以根据不同的需求切换到不同的阶段，得到不同精度的视差图，从而实现由粗到细的三维重建。

算法网络如表4所示。

表4 算法网络Tab.4 Algorithmic network

本文采用的立体匹配算法与其它算法的对比如表5和表6所示，其中，表5为不同算法在KITTI2015数据集上的测试结果，其中根据是否为遮挡区域可分为All和Noc：All表示全图区域，Noc表示非遮挡区域；根据其为背景、前景和全图区域可分为D1-bg、D1-fg和D1-all这3种情况，评价指标都为3PE。由表5可以看出：本文算法比文献[5]中MC-CNN、文献[17]中Content-CNN、文献[6]中psNetC算法效果要好，比文献[8]中GC-Net、文献[18]中iResNet算法性能要稍差，但其运行时间较快，仅为0.02 s。表6是与文献[8]中GC-Net、文献[18]中iResNet这两个典型的立体匹配算法在SceneFlow数据集上的对比，可见其端点误差降低，参数量仅为0.5×106。

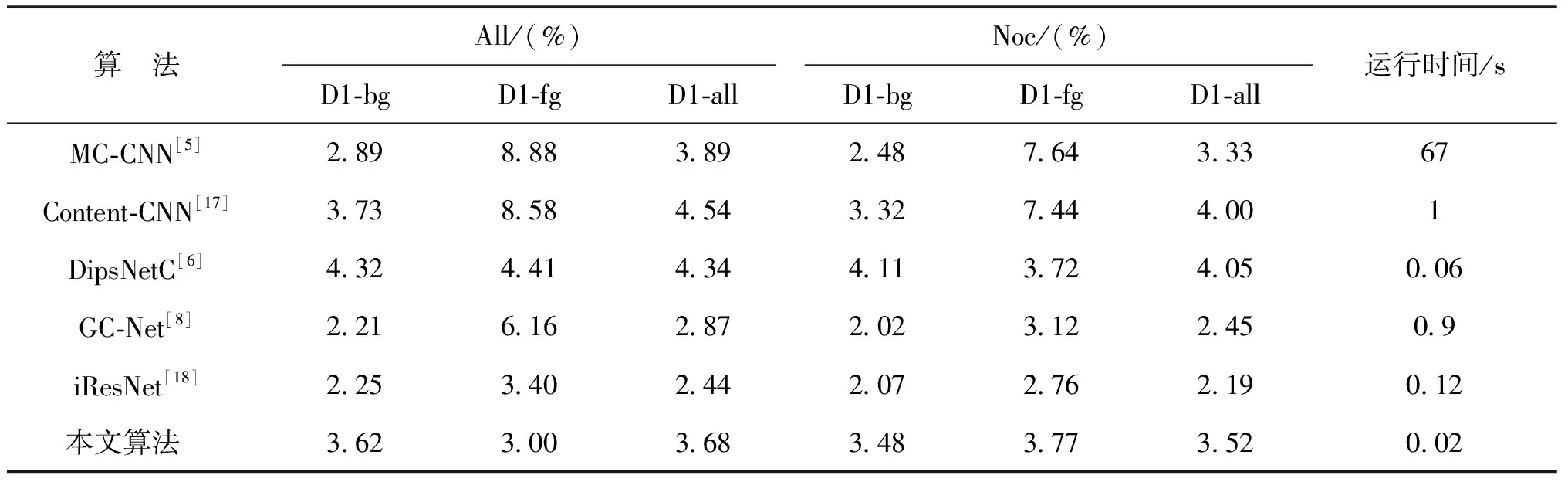
表5 在KITTI2015数据集的测试结果Tab.5 Test results on the KITTI2015 dataset

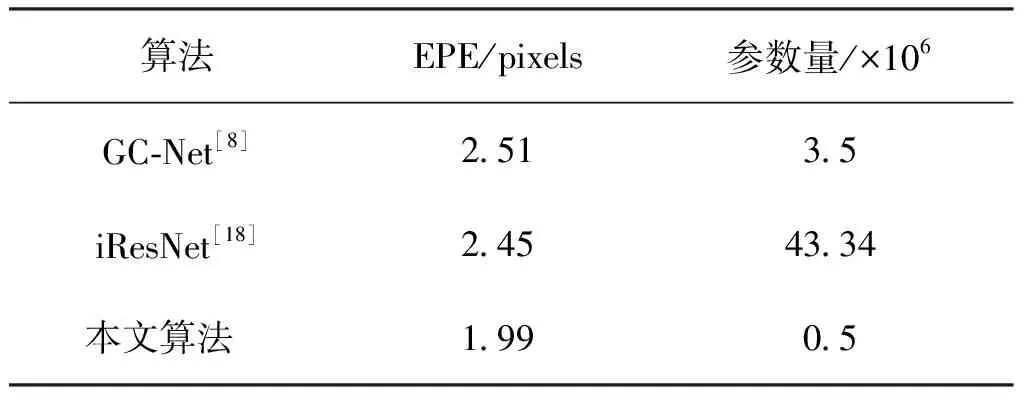
表6 在SceneFlow数据集的测试结果Tab.6 Test results on the SceneFlow dataset

4.3 三维重建实验

实验是在室内实现目标立体视觉的三维检测与重建。待检测的目标是桌面上的杯子，采用前面标定的双目摄像机进行左右两幅图像采集，利用可变形卷积立体匹配算法获得3个阶段的视差图。利用视差与深度的转换关系来得到物体深度值Z:

Z=(Bf)/d

(18)

式中：B表示双目相机的基线；f表示焦距;d为视差值。

杯子深度图的测试结果如图8所示。得到3个阶段的深度图之后，在Open3D上对杯子进行三维重建，重建效果如图9所示。

图8 杯子深度图Fig.8 Cup depth map

图9 3个阶段的三维重建效果Fig.9 Three-stage 3D reconstruction effect

由重建的结果来看出：每一阶段的物体轮廓都基本显示出来，一个阶段比一个阶段重建的效果好。

5 结 论

本文提出了一种基于可变形卷积的立体匹配算法，与其他典型的基于深度学习的立体匹配算法相比，该算法不仅参数量少，仅为0.5×106，而且运行时间也最短，只有0.02 s，可以用于像机器人导航这类视场中的三维物体的快速重建。还可以根据不同的等级需求，切换到不同的阶段生成不同精度的视差图来进行三维物体重建，能够满足不同场合立体视觉的实时需求。