角速度有界的在轨抓捕航天器姿态控制
2022-07-21徐琳代睿殷春武段中兴
徐琳, 代睿, 殷春武, 段中兴
(1.西安建筑科技大学 信息与控制工程学院, 陕西 西安 710055;2.西北工业大学 自动化学院, 陕西 西安 710129)
随着人类空天活动的增加,漂浮在太空中的空间碎片对在轨航天器的威胁也与日俱增,因此清除空间碎片(或其他非合作目标)成为航天领域可持续发展必须解决的问题。最常用的清除方式是采用机械臂捕获并回收空间碎片,在此过程中航天器会因机械臂运动而出现质心偏移和姿态偏差,因此设计出具有较强鲁棒性的自适应控制器,从而保证抓捕航天器的安全运行,具有重要的工程应用价值。
无序飞行的空间碎片其质量与速度均未知。航天器在抓捕空间碎片过程中,航天器的质心必定发生偏移,从而导致转动惯量摄动量变化规律不可预知。因此,必须采用自适应控制技术或智能逼近系统对转动惯量摄动部分进行补偿,提升系统对参数摄动的鲁棒性。文献[1-5]主要是设计自适应律实时估计未知转动惯量,并基于不同的应用环境构建包含转动惯量估值的自适应姿态控制算法;文献[6-8]则主要将转动惯量分离为名义部分和摄动部分,并采用诸如极限学习机、神经网络、模糊系统等智能逼近系统逼近由转动惯量摄动引起的摄动部分,并将其作为控制器的补偿性输入。以上研究工作虽然都解决了参数摄动问题,但所用算法均存在转动惯量估计精度不足、智能逼近系统结构复杂等缺陷。
在抓捕空间碎片过程中,不仅存在转动惯量摄动问题,还存在导航带宽和角速率陀螺量程的限制问题,因此航天器的角速度必须限制在有界范围内。早期学者重点关注的是航天器控制输入饱和约束的解决方案[9-13]。近些年,航天器角速度有界约束的研究才被重视[14-17]。文献[14]在考虑航天器角速度有界和转动惯量摄动条件下,设计了一种反演自适应控制算法;文献[15]基于抗退绕控制方法提出了角速度和控制输入有界的控制算法;文献[16]给出了一种L2增益控制算法,文献[17]设计了一种改进的非线性反馈控制器。
本文以航天器捕获非合作目标过程中的姿态稳定控制为应用背景,在考虑航天器角速度有界约束条件下,采用双环递归跟踪控制方法,设计出航天器自适应跟踪控制器。设计思路如下:对航天器外环系统的姿态运动学方程预设了一个有界虚拟角速度作为外环虚拟控制的输入,使得外环系统姿态角能够平稳快速收敛至期望角度;对于航天器内环系统,本算法基于矩阵变换算子将转动惯量矩阵转换成关于转动惯量元素向量的回归方程,构建自适应更新律在线估计上界未知的转动惯量;根据包含角速度跟踪误差的障碍李亚普诺夫函数(barrier Lyapunov function,BLF),设计出自适应姿态控制器,驱动实际角速度快速跟踪外环预设虚拟角速度,同时保持角速度的有界性。
1 抓捕控制问题描述
刚体航天器在抓捕非合作目标过程中,质心偏移导致的主转动惯量的变化规律可描述为:
1) 在抓捕过程最初阶段,主转动惯量会随着机械臂伸展而逐渐增加;
2) 在捕获非合作目标瞬间,非合作目标的无序运动反作用于航天器,导致主转动惯量产生一个未知的突增;
3) 在机械臂回收阶段,主转动惯量则会逐步递减。
令航天器在捕获非合作目标瞬间受到的瞬时强干扰为d1。再考虑外部环境干扰d2,则抓捕航天器的实际外部干扰为
d=d1+d2
(1)
基于单位四元数{q0,q}={q0,q1,q2,q3}的航天器姿态运动学的方程式为[2]
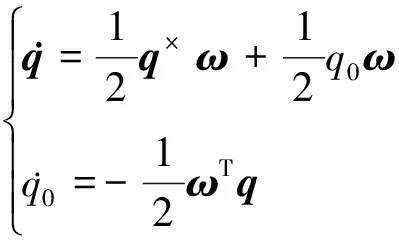
(2)
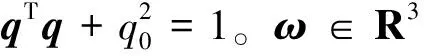
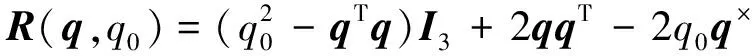
(3)
式中:I3为单位矩阵;R为单位正交矩阵。
刚体航天器姿态动力学方程为[2]
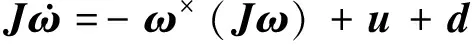
(4)
式中:d∈R3为(1)式中的有界外部干扰,且‖d‖∞≤D,常数D为干扰最大值;u∈R3为控制输入矢量。转动惯量矩阵J分解为名义矩阵J0和摄动矩阵ΔJ,即J=J0+ΔJ。由于非合作目标的动力学特性不可预知,所以转动惯量J的上界未知。ω×为矢量ω=[ω1,ω2,ω3]T的反对称矩阵
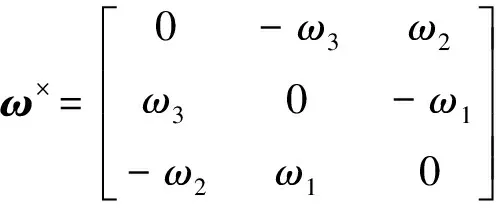
(5)
那么可以把航天器在轨抓捕非合作目标时的姿态控制问题转换为:当存在外部干扰d和转动惯量J摄动的复杂条件下,基于航天器动力学系统(2)与(4)设计鲁棒控制器u,使闭环系统渐近稳定。即当t→∞时有
q(t)→0,ω(t)→0
(6)
且角速度满足约束‖ω‖∞≤ωmax。
2 相关定义和引理
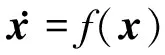
1) 当x∈Ω趋近于Ω的边界时(如‖x‖→kb),有V(x)→∞;
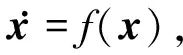
则定义函数V(x)为障碍李亚普诺夫函数。
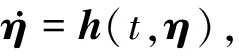
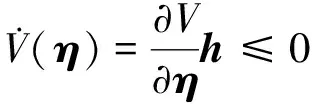
(7)
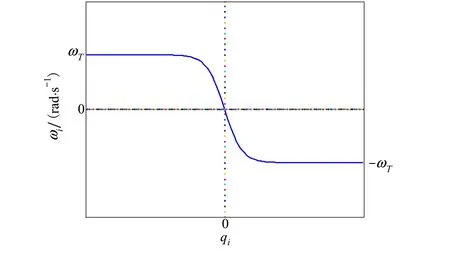
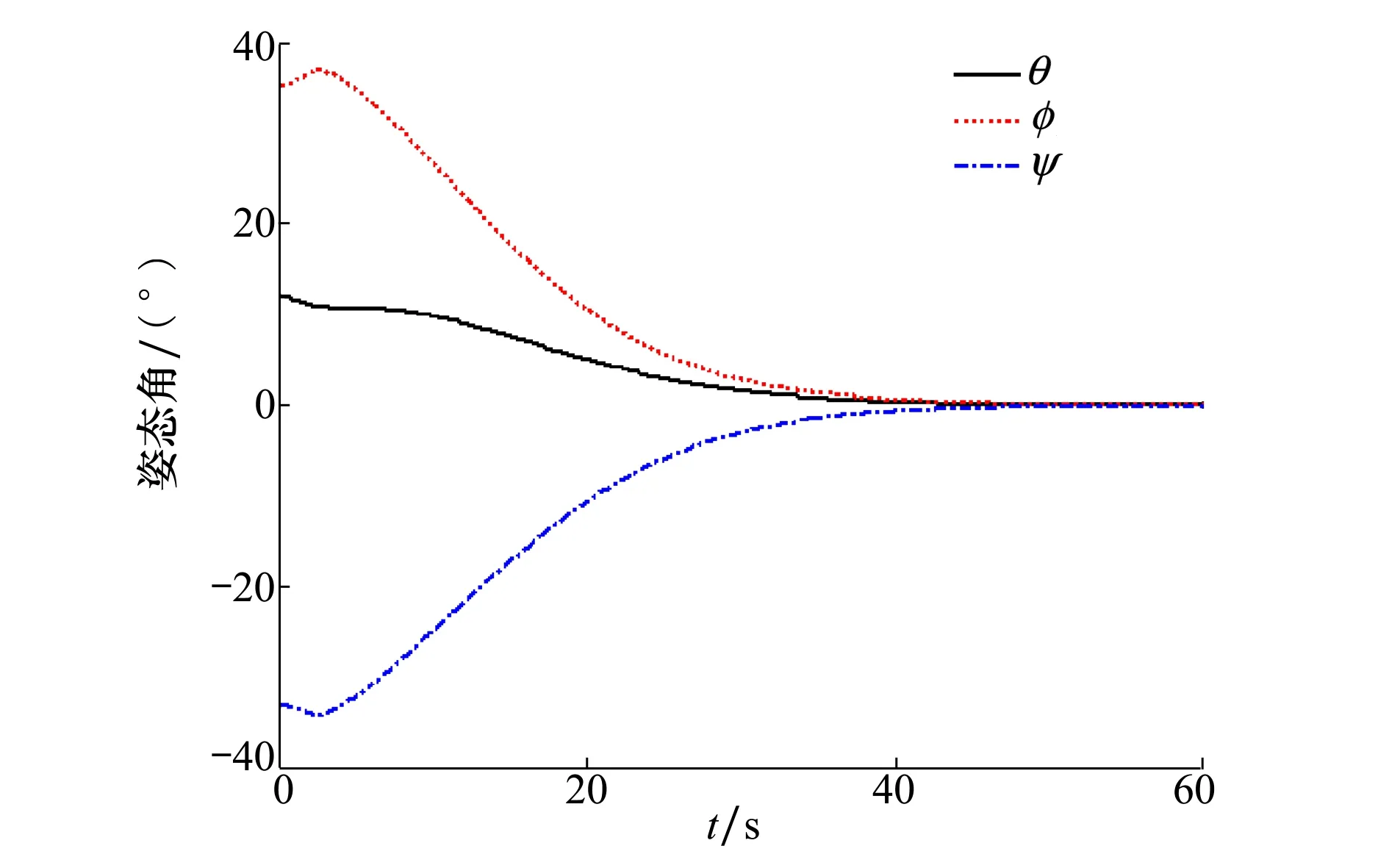
则对于t∈[0,∞)有‖e1(t)‖ 定义2令向量a=(a1,a2,a3)T,定义线性回归算子 (8) 令ξ=(J11,J22,J33,J12,J13,J23)T,则有 (9) 本文采用双环递归跟踪控制方法设计航天器的姿态跟踪控制器,并分别对闭环系统的稳定性以及角速度的全程有界性进行理论推导。 考察以角速度作为输入量的外环运动学方程。一方面,过大的角速度会破坏航天器的平稳性,另一方面,受航天器物理硬件设备的限制,角速度难以达到较大的理论数值,因此,为设计更符合工程应用的姿态跟踪控制器,必须要求角速度有界。为了限定外环系统中角速度的输入范围,本文设计有界虚拟角速度输入 ωv=-ωTtanh(k1q) (10) 式中,ωT>0为外环运动学方程中可允许的最大虚拟角速度值,常数k1>0。图1反映了ωv某一分量的变化特性。 图1 虚拟角速度分量的变化特性 如前文所述,为了确保外环系统(2)的渐近稳定性,本文预设了虚拟角速度ωv。由此构造出Lyapunov函数 V1(q)=(q0-1)2+qTq (11) 对V1(q)关于时间t求导 (12) 可见,当实际角速度ω为虚拟角速度ωv时,有 (13) 根据Lyapunov第二稳定性理论可知,当t→∞时,q0→±1,q→0。 设ω为内环系统(4)输出的实际角速度。内环自适应控制器u的设计目标为:能够实现ω快速跟踪预设有界虚拟角速度ωv。 设e为ω与ωv的跟踪误差 e=ω-Rωv (14) 构造如下BLF函数 (16) (17) 式中 (18) 将(17)式代入(16)式得到 (19) 当转动惯量J已知时,设计姿态控制器 u=-Yξ-Dsign(e)-k2e (20) 式中,常数k2>0,sign(·)为符号函数。将(20)式的控制输入表达式代入(19)式得到 (21) 根据(21)式可知,在转动惯量矩阵J已知时,若t→∞,则有e→0,即 (22) 证毕 至此,内环子系统和外环子系统在其各自控制输入下,各闭环系统的稳定性得证。接下来证明双环递归控制下闭环系统的稳定性。 定理1当转动惯量J已知时,姿态控制器(20)式能保证航天器姿态控制系统(2)式,(4)式渐近稳定,且当t→∞时有q(t)→0,ω(t)→0。 -ωTqTRq+qTe= qTe=-ωT‖q‖2+qTe≤ (23) (24) 对(24)式在[0,∞]上积分,并将V1(q)=(q0-1)2+qTq=2-2q0(t)代入,得 (25) 证毕 推论1当转动惯量J已知时,在控制器(20)作用下,对于t∈[0,∞),ω与ωv的跟踪误差满足‖e(t)‖∞<ωe。 根据e=ω-Rωv,‖ωv‖∞≤ωT有‖ω‖∞≤‖e‖∞+‖ωv‖∞,结合推论1可以得到: 推论2当不存在摄动对转动惯量J的扰动时,对于ωe∈[0,∞),ωT∈[0,∞),总可以选择出适当参数,使得ωe+ωT≤ωmax成立。因此在姿态控制器(20)作用下,实现对航天器角速度的有界约束,即角速度‖ω‖∞≤ωmax。 推论3当转动惯量J已知,控制增益k1,k2一定时,控制输入力矩是有界的,且满足 (26) 因为 ‖u‖∞≤‖Yξ‖∞+ ‖Dsat(e,ε)‖∞+‖k2e‖∞≤ ‖ω×Jω‖∞+‖Jω×Rωv‖∞+k2ωe+ λJmax‖ω2‖∞+λJmax‖ω‖∞‖ωv‖∞+ (27) 由于符号函数容易引起抖振,因此控制器中的符号函数可以用饱和函数代替,则(20)式修正为 u=-Yξ-Dsat(e,ε)-k2e (28) 其中饱和函数sat(e,ε)分量元素的定义为 (29) 前文在转动惯量J固定前提下,设计了航天器姿态控制器(20),而航天器在轨捕获非合作目标过程中,因受到目标本身无序运动的干扰,其转动惯量会出现不同程度摄动。下面针对转动惯量发生改变的工程应用背景,构建自适应姿态稳定控制器。 (30) (31) 自适应姿态控制器表达式为 (32) 将(32)式代入(31)式得到 (33) (34) 则有 (35) 当自适应控制器(32)和自适应更新律(34)应用于航天器姿态控制时,根据Lyapunov稳定理论可知,闭环系统(4)渐近稳定。同理,带饱和函数的自适应姿态控制器为 (36) 根据定理1,同样可得如下定理2。 定理2对存在转动惯量摄动和外部干扰的航天器姿态动力学系统,自适应控制器(32)与自适应律(34)可实现闭环系统的渐近稳定性保证,即当t→∞时有q(t)→0,ω(t)→0。 定理2证明与定理1相同。同理可得如下推论。 推论4转动惯量J存在未知摄动时,应用自适应姿态控制器(32)与自适应更新律(34),当t∈[0,∞)时,‖e(t)‖∞<ωe,其中e(t)为实际角速度ω与虚拟角速度ωv之间的误差。 推论5当存在未知摄动对转动惯量J的扰动时,对于ωe∈[0,∞),ωT∈[0,∞),总可以选择出适当参数,使ωe+ωT≤ωmax成立。因此在自适应控制器(32)与自适应更新律(34)的作用下,航天器的角速度有界,即‖ω‖∞≤ωmax。 推论5说明自适应姿态控制器(32)和自适应更新律(34)实现了在轨捕获非合作目标过程中的姿态稳定控制和角速度有界约束的目标。为保证闭环系统的收敛性和角速度的有界性,在设计ωe,ωT时,应尽可能地增大角速度追踪误差上界ωe,减小虚拟角速度的变化幅度值ωT。 自适应控制器(20)和(32)中的增益系数k1,k2恒定时,为避免当姿态追踪误差较大时产生过大控制力矩,本文对自适应控制器中的参数采用如下变增益表达式 ki=ρieαiarctan(βit)i=1,2 (37) 式中,参数ρi,αi,βi>0(i=1,2)。其中,控制增益增长速度的参数为αi;用来控制增益取值范围的参数为ρi;控制增益收敛速度的参数为βi。 在抓捕非合作目标的过程中,假设在时刻T0=10 s时成功捕获无序运动的非合作目标,此时会对抓捕航天器产生一个瞬间强干扰d1(其中r为方波),外部太阳辐射等环境干扰力矩记为d2(单位:N·m,ωΔ=0.1) 在T1=25 s时刻,非合作目标被抓捕航天器成功回收。结合实施抓捕的机械臂的动作过程,转动惯量各元素变化规律可以表示为 采用Matlab进行数值仿真,图2~4为数值仿真结果。 图2 姿态角变化趋势(双环) 图2中的曲线反映了航天器姿态角变化趋势。从图2可以看出,基于本文所设计的变增益自适应姿态控制器(36),航天器的姿态角呈指数渐近收敛到0,且整个收敛轨迹没有震荡。即便在第10 s抓捕非合作目标时出现一个瞬时强干扰,且整个抓捕过程中转动惯量J的元素呈非线性摄动,但航天器的姿态角收敛趋势并没有受到干扰和参数摄动影响。说明自适应控制器(36)具有较强的鲁棒性,能够使抓捕非合作目标过程中航天器姿态快速稳定。 图3为抓捕过程中的控制力矩变化曲线。图3显示即便初期姿态角偏差较大,但由于变增益函数提供较小的控制增益,使得刚开始的控制力矩在保证姿态角收敛的前提下,控制力矩较小;后期虽然控制增益较大,但是姿态角追踪误差减小了,使得控制力矩也较小,整个控制过程中,除第10 s外,其他时间段的控制力矩均保持在-8~5 N·m内,且力矩的频繁震荡相对较少。在第10 s出现瞬间强干扰时,控制力矩产生了一个较大的控制输入力矩来抑制外部强干扰,并在强干扰消失后,控制输入力矩迅速减小。 图3 三轴控制力矩曲线(双环) 图4反映了实际角速度ω跟随预设虚拟角速度ωv变化的跟踪效果。在控制初期,ω与ωv存在追踪误差,但在本文设计控制器下,ω很快收敛到ωv,并按照ωv的轨迹收敛到0 rad/s。在整个抓捕非合作目标过程中,航天器的角速度满足有界约束条件‖ω‖∞≤0.03 rad/s≤0.1 rad/s,且角速度追踪误差满足‖e‖∞<0.05 rad/s。在第10 s出现外部强干扰时,真实角速度ω受到微弱干扰,随着干扰消失,真实角速度会快速收敛到ωv。 图4 ω和ωv轨迹曲线 仿真结果表明,在存在外部干扰和转动惯量矩阵各元素呈非线性摄动的情况下,控制力矩根据实际角速度ω与虚拟角速度ωv之间的误差,控制ω快速追踪上ωv,并按照ωv的轨迹变化。当姿态角较大时,ωv以较大的输入驱动姿态角迅速减小,并随着姿态角的收敛而逐渐收敛到0 rad/s。仿真结果显示,本文设计的鲁棒姿态控制器具有理想的控制效果,能保障抓捕过程中航天器的角速度满足有界限制和航天器的姿态快速机动。 4.2 对比仿真分析 为验证本文的双环跟踪控制器与反演控制器的区别,在相同控制器设计思路下,设计反演控制器。设计Lyapunov函数为V4(e)=V1(e)+V3(e),对V4(e)求导,有 反演自适应控制器为 (38) 当控制器为反演控制器(38)时,其他控制参数不变,得到仿真结果如下: 图5 姿态角变化趋势(反演) 图6 三轴控制力矩曲线(反演) 通过对比图2和图5,图3和图6可以看出,姿态跟踪轨迹和控制力矩的变化趋势几乎相同,说明在相同仿真条件和控制参数下,反演控制与双环跟踪控制器的控制效果相同。但相对于反演控制器的复杂结构,本文设计的双环跟踪控制器结构更为简单。 本文以存在角速度有界约束的抓捕非合作目标航天器的姿态稳定控制为研究对象,结合双环递归追踪控制思想,在转动惯量固定和转动惯量摄动2种环境下,设计了航天器姿态鲁棒控制器,并分析了所设计控制器能保证航天器角速度的有界性。 1) 将航天器的二阶姿态动力学系统分解为外环、内环2个一阶子系统,并分别为这2个子系统设计各自的轨迹跟踪控制器,进而构建出一种双环递归跟踪控制器。通过理论分析和推导,证明此二阶系统的渐近稳定性。相比于反演控制器,双环追踪控制器具有结构更简单,其控制器设计的自由度更高等优点。 2) 对于转动惯量固定和转动惯量存在未知摄动的2种情况,应用BLF函数分别设计了相应的航天器姿态稳定控制器。通过理论分析和推导,证明该闭环系统具有渐近稳定性以及角速度有界性。数值仿真了捕获非合作目标过程中的姿态稳定控制情况,结果显示在本文设计的自适应姿态控制器作用下,抓捕航天器的姿态角与角速度实现了平缓收敛且无振荡,展示出良好的动态品质。 3) 通过推论3可以看出,针对转动惯量上界已知的航天器姿态控制,可以估算出基于本控制器的最大控制输入力矩,对航天器执行机构的设计具有一定的指导作用。 4) 航天器在受较大瞬间冲击力矩时,航天器姿态没有改变,说明本文所设计控制器对瞬间强干扰不敏感。

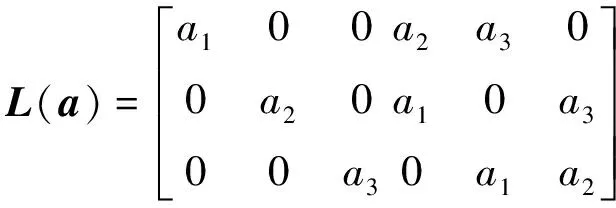
3 控制器设计
3.1 外环控制器设计
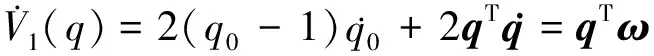
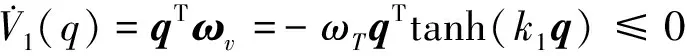
3.2 内环鲁棒追踪控制器设计
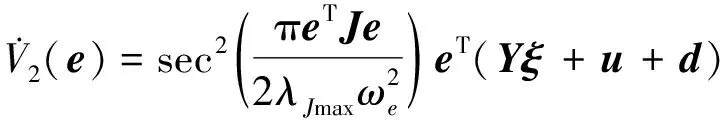
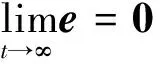
3.3 双环追踪控制稳定性分析

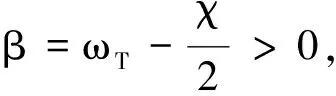
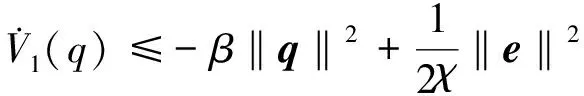

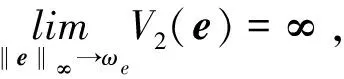
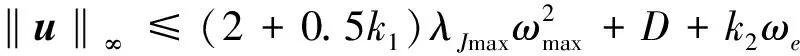
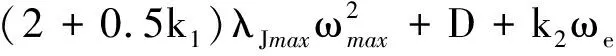

3.4 内环自适应追踪控制器设计
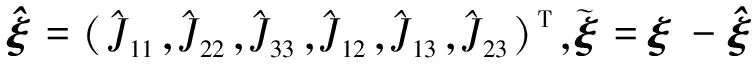
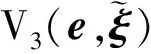
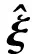
4 数值仿真分析

4.1 验证仿真分析
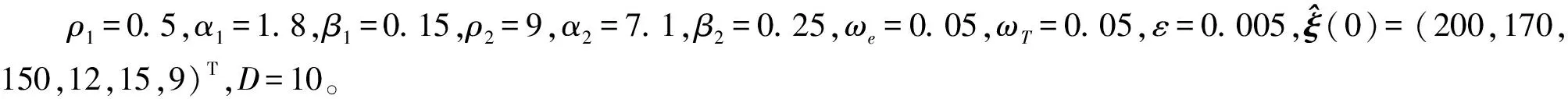



5 结 论
