斜入射地震下预制拼装管廊地震响应分析
2022-07-21夏樟华唐永波林友勤许有胜
夏樟华,唐永波,林友勤,许有胜
(1.福州大学土木工程学院,福建福州 350108;2.深圳市市政设计研究院有限公司,广东深圳 518035)
引言
地下综合管廊,又称共同沟,是将燃气、电力、电信、给排水等2 种或2 种以上的生命线工程设施共同敷设于其中的地下结构[1]。发展建设地下综合管廊已成为现代城市可持续发展的重要方向,而地下综合管廊抗震性能研究具有重要的理论和现实意义[2]。早期日本学者Kawashima、高田至郎等[3-4]就讨论了综合管廊等地下结构在地震下反应的问题和土层液化下综合管廊的破坏机理并给出了对应的整治措施。近些年来我国学者也开展了相关研究,岳庆霞[5]研究了地下结构地震波的输入形式,通过对比得出较为精确的位移输入方式;史晓军等[6-8]开展了地下综合管廊大型振动台试验研究,介绍了试验方法、试验结果以及数值模拟;冯瑞成[9]开展了共同沟模型试验并进行了抗震性能的评价;黄臣瑞[10]采用数值模拟方式,指出纵向接头弯曲刚度和轴向刚度是影响结果的关键因素以及行波激励显著增大了预制管廊的地震响应;梁建文等[11]研究了地下T 型交叉管廊的地震响应,指出T 型交叉管廊的交界面内力最大;此外,杨仕升等[12]针对管廊的典型节点进行了抗震研究,得出管廊节点在地震下具有良好的整体性,节点隔板与底板及中板、侧壁与底板及中板为管廊的薄弱部位。可见,常规垂直入射下地下结构响应分析已较为成熟。
实际地震动在传播中存在非一致性,通常假定处于工程近场处深源地震是以垂直基岩形式入射的平面体波,而处于工程远场处的浅源地震系以一定的角度传播至近场,即斜入射。斜入射相较于垂直入射由于行波效应存在着更为复杂的波场叠加情况,对于管廊等地下结构,斜入射地震作用下存在着更为复杂的响应。同时实际工程也表明,斜入射SV波相较于斜入射P波具有更大的破坏性,因此建立SV波斜入射的地震输入方法并运用于实际工程进行地震响应的研究是有必要的[13-14]。目前国内外学者对于综合管廊的地震响应分析大多数基于垂直入射的假定,对于斜入射地震波下管廊的地震响应较少。文中基于粘弹性边界时域波动方法,阐述在三维空间下SV波沿一定角度入射的地震输入方式,同时结合Auto_VSB辅助程序实现斜入射地震节点力的转化,最后基于该地震输入方法对预制节段拼装综合管廊进行地震响应研究。
1 预制拼装管廊有限元建模分析
1.1 背景工程
以某试验区环湖路综合管廊工程为背景,综合管廊截面采用单仓结构形式,标准段管廊断面大小为3.9 m×4.1 m,顶底板及腹板壁厚35 cm。管廊标准段结构如图1所示。

图1 管廊截面图Fig.1 Sectional view of utility tunnels(Unit:cm)
1.2 整体有限元模型
有限元模型是基于ABAQUS 平台建立的三维实体模型[15],土体、结构均采用实体模型C3D8R 进行模拟,钢筋及预应力钢绞线均采用TRUSS单元进行模拟,两端采用MPC 约束进行端点耦合,并通过初始应力法来施加预应力,其中预应力根据工程实际取150 kN。在进行地下结构抗震数值分析时,土 体模型的长度截取十分重要,由于文中模型采用粘弹性边界,有效地削弱了边界对计算结果的影响,并模拟了远域土体的特性,故近场土体的截取可适当缩小尺寸。因此在土体的截取采取如下原则:管廊结构左右两侧距离土体边界均需大于3 倍管廊宽度,管廊结构底部距离基岩面需大于3 倍管廊高度,纵向长度取6 节管廊长度即12 m。综上所述,土体模型尺寸为28 m×12 m×20 m,整体有限元模型及管廊精细模型如图2及图3所示。

图2 整体有限元模型Fig.2 Overall finite element model(Unit:cm)
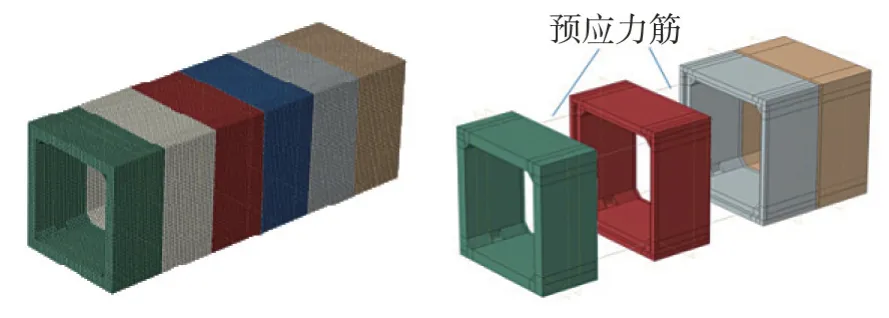
图3 管廊有限元模型Fig.3 Finite element model of utility tunnels
1.3 土体动力特性本构
在地下结构的抗震分析中可采用非线性和等效线性动粘弹性模型来模拟土体本构2种方式。由于非线性本构所需的计算参数较为复杂,且计算耗费时长较长,等效线性方法可以通过不断迭代逼近来反应土体非弹性与非线性以取得预期效果,该方式计算高效,且在地震加速度小于0.4 g 的情况下能提供较为合理的结果。故文中采用等效线性动粘弹性模型来模拟土体本构。
在ABAQUS 中没有自带等效线性本构,需要通过UMAT 用户子程序进行编写导入。UMAT 用户子程序系采用FORTRAN 语言编写,用户需提供材料积分点雅克比矩阵以完成本构关系的开发。在文中采用UMAT用户子程序的过程如下:
(1)通过*initial conditions,type=solution 导入各单元有效应力,作为状态变量STATEV(1),在后续分析中供UMAT子程序调用;
(2)在UMAT子程序中将单元最大剪应变存储为STATEV(2);
(3)通过编写的FORTRAN 语言将根据应变水平确定的等效剪切模量和等效阻尼比存储为状态变量STATEV(3)和STATEV(4);
(4)最后将4个状态变量作为初始变量替换第一步中*initial conditions,type=solution 导入的变量来完成迭代计算。
1.4 动力接触分析
在基于SSI(soil-structure interaction)效应下的地下结构动力计算中,接触作用扮演着至关重要的角色。动力接触问题是一个高度复杂的力学不连续性问题,在非线性问题求解中,每次增量分析都须判断接触面的接触状态,进而不断连续迭代的过程。目前常用的动力接触数值算法有Lagrange 乘子法、修正Lagrange 乘子法、罚函数法和线性补偿法。文中管廊结构与土体接触采用面面接触,并采用罚函数法进行求解。
1.5 地震波的选择
由地勘资料可知,本工程拟建场地抗震设防烈度为7 度,基本地震加速度值为0.10 g,设计分组为第三组,场地类别属Ⅱ类区段,反应谱特征周期为0.45 s。结合《建筑工程抗震性态设计通则》推荐[16],主要采用Kobe 波对预制节段拼装综合管廊进行抗震分析,同时根据《GBT 51336-2018 地下结构抗震设计标准》[17],并根据相应的分析需要对该组地震波进行加速度幅值调整,分别调整为0.1、0.2、0.3 g。
加速度幅值调整具体公式如下:


图4 Kobe波加速度时程曲线Fig.4 Kobe wave acceleration time history curve
1.6 阻尼理论
在结构的动力分析中,阻尼的作用不容忽视,阻尼根据生成原因分为内阻尼和外阻尼。阻尼的存在能够使结构的振动衰减以及能量耗散,对于结构的抗震起着有利的作用,目前ABAQUS 常用的阻尼有直接模态阻尼、瑞利阻尼、复合模态阻尼和结构阻尼,文中采用瑞利阻尼进行阻尼模拟。庄海洋[18]认为土体的非线性计算分析中,只需考虑土体材料的粘性效应,按瑞利计算,通常土体阻尼比取2%;混凝土阻尼比为5%。
1.7 土结共同作用动力方程及求解
结构动力平衡方程与静力平衡方程类似,区别在于动力平衡方程需在单元中考虑阻尼以及惯性力的影响。
在结构物未形成前,自由场情况下土-基岩运动方程:

式中:UC是自由场位移向量;Mf是自由场质量矩阵;Kf、Cf分别为对应的刚度矩阵及阻尼矩阵;{Pe(t)}为有效地震力。

当结构物形成时,土-结构体系运动方程如下:
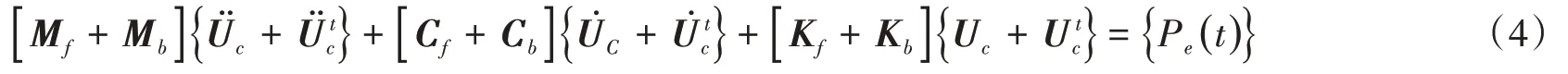
式中:Mb、Cb、Kb分别为结构物的质量矩阵、阻尼矩阵、刚度矩阵;Ut c表示结构物产生的反作用运动。
动力平衡方程的求解方法包括振型叠加法、复反应分析法和逐步积分法。ABAQUS 隐式动力计算采用的是逐步积分法中的Newmark-β法,为求解非线性问题提供一个良好稳定的平台。
2 粘弹性人工边界及Auto_VSB辅助程序
2.1 场地土模拟的边界问题
在进行地下结构动力分析时,目前常用的人工边界分2 类,一类是全局边界,另一类是局部人工。虽然前者具有高精度的特点,但方程的耦合性使其在求解硬件上要求较高,适用性上有较大的局限性;目前常用的局部人工边界有黏性边界、透射边界、粘弹性边界[19-20]。文中所采用的是局部人工边界中的粘弹性边界。
2.2 粘弹性边界的设置
集中粘弹性人工边界的具体实现方法是在边界处离散分布弹簧和阻尼器,分别用来模拟边界远域处弹性恢复性能和抵消散射波在边界处的反射效应,在ABAQUS 隐式算法中采用Springs和Dashpots来实现弹簧和阻尼器的添加,即在边界节点处使用Springs和Dashpots代替传统静力边界,完成动力边界的建立。
三维粘弹性人工边界(见图5)系在球面坐标上进行推导,忽略波的汇聚性仅考虑剪切波在球面上扩散时,设切断截面r=R,则其三维粘弹性人工边界的弹簧刚度及阻尼系数由式(5)和式(6)确定,

图5 三维粘弹性边界示意图Fig.5 Schematic diagram of three-dimensional viscoelastic boundary

式中:KT和CT人工边界上切向弹簧刚度和阻尼系数;KN和CN分别为法向弹簧刚度和法向阻尼系数G 为剪切模量;R为切断面半径;ρ为地基质量密度;Cs和Cp分别为S波和P波波速。
2.3 三维粘弹性人工边界等效节点力的转化
施加粘弹性边界后,预设外传散射波被边界完全吸收,此时若是直接在基底施加位移时程,则将产生波的反射,即在边界处产生弹簧阻尼反力,故采取的方法是将外源地震动转化为等效节点力,同时抵消弹簧阻尼反力,现以三维边界为例,等效节点力可用下式进行计算。

式中:Kb和Cb分别为弹簧刚度及阻尼系数对角矩阵分别为自由场位移向量、速度向量以及应力张量;Ab为边界节点影响面积。
2.4 斜入射人工边界内行场位移
同垂直入射粘弹性人工边界,采用方形边界替代球形边界以更贴近实际工程,图6 为三维平面SV 波斜入射示意图,并假设SV 波波阵面平行于人工边界地面的一条棱。由图6 可得出边界面上各点的内行场情况,其中前后边界及左边界的内行场构成为斜入射的SV 波和地面反射的SV 波及P 波,属于自由场;底面边界的内行场的构成仅为斜入射的SV 波;右面边界无内行场[21]。

图6 三维平面SV波斜入射示意图Fig.6 Schematic diagram of three-dimensional plane SV wave oblique incidence
考虑斜入射传播非一致性的特点,地震波传播到各个位置的过程存在着时间差,则左侧边界的内行场中的入射角为α的SV波、反射角为α的SV波及反射角为β的P波时程分别为u0(t-Δt1)、A3u0(t-Δt2)A4u0(t-Δt3)则左侧边界内行场位移为:

前后边界的内行场中的入射角为α的SV 波、反射角为α的SV 波及反射角为β的P 波时程分别为u0(t-Δt4)、A3u0(t-Δt5)、A4u0(t-Δt6),则前后边界内行场位移为:

底边边界的内行场仅存在着时程为u0(t-Δt7)的入射角为α的SV波,则底边内行场位移为:

式中:A3为反射SV 波与入射SV 波幅值的比值;A4为反射P波与入射SV 波的幅值的比值;u0(t)为入射波位移时程,各边界面上的y方向位移u均为0;Δt1-Δt7分别为左侧边界的直接入射SV波、地表反射SV波、地表反射P波和前后边界的直接入射SV波、地表反射SV波、地表反射P波及底边界相对于入射波u0(t)初始时刻的延迟时间,可由式(11)计算而得:

式中:左侧边界结点的坐标为(0,y);底边界结点的坐标为(x,0);L为左边界的高度。
2.5 斜入射人工边界内行场应力
当已知各边界内行位移场便可推导出内行应力场。
其中左侧边界应力场为:
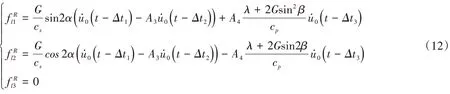
前侧人工边界应力场为:

后侧人工边界应力恰好与前侧应力相反。底部边界应力场为:

式中:CP和CS分别为P波和SV波的波速;λ和G为拉梅常数。
2.6 基于python语言的粘弹性人工边界辅助程序Auto_VSB
根据上述分析,只要已知节点控制面积以及外源波位移时程和速度时程,便可以求得等效点力,然后通过ABAQUS 的*Cload 和*Amplitude 来实现节点力的输入,但是由于模型体量巨大,节点众多,无论是节点力的求取还是施加都是一个复杂且浩大的工程,重复率高且容错率低,传统的计算方式是结合Matlab 编制简单的计算程序,再通过一系列复杂的程序完成。值得一提的是Matlab 是基于矩阵计算的程序语言,转换效率较为缓慢,一个地震波工况的转换通常耗时10~20 min,在非线性计算中效率极低。文中结合上述需求基于python 编程语言,编制了粘弹性人工边界及节点力自动施加程序Auto_VSB(Automatic Viscous-Spring Boundary)。所编制的Auto_VSB辅助程序拥有简单的操作界面(如图7),用户仅需输入一些简单的场地物理条件,包括坐标、弹性模量等参数,结合用户放入的任意地震波位移时程及速度时程等文件,即可实现粘弹性边界及节点力文件的快速生成。每条地震波转换耗时仅需要3 s,极大地提高了效率。

图7 Auto_VSB程序界面Fig.7 Auto_VSB program interface
2.7 基于Auto_VSB辅助程序的斜入射地震输入的精度验证
基于以上地震力输入方法,将斜入射节点力自动计算功能内置于Auto_VSB 辅助程序中,为了验证该程序所建立的斜入射方法精度,建立长×宽×高为400 m×400 m×600 m三维土体,离散单元网格为20 m×20 m×20 m,土体弹性模量E=4.88 GPa,密度ρ=2 000 kg/m3,泊松比ν=0.22,外源波步长取0.01 s,历时2 s,分别以入射角为15°和30°入射SV波脉冲,脉冲方程式为:

式中:μ为位移;t为时间。
图8为施加了粘弹性边界及斜入射节点地震力幅值的验证模型图,由于地震力由左侧入射,故右侧不存在节点力幅值。图9 是入射角为15°和30°下的验证模型应力云图。图10 为入射角为15°和30°时验证模型底部中点和顶部中点位移时程图。可以看出斜入射输入方式随着入射角度的变化会产生不同的结果,叠加规律较为复杂,由于斜入射波从左下角入射,传播至顶部中点及底部中点均需时间,故底部中点位移时程不是从0 s开始,且顶部中点位移时程与底部位移时程存在时间差延迟,两种不同角度的入射波折射反射的叠加方式不同,但最终波都由边界吸收归为0。
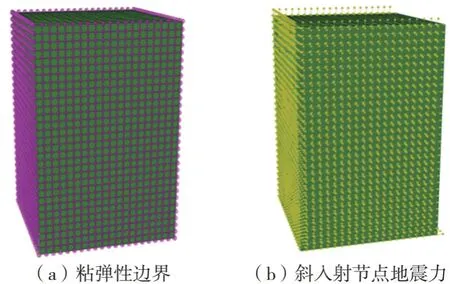
图8 斜入射地震波下粘弹性边界验证模型Fig.8 Validation model of viscoelastic boundary under obliquely incident seismic waves

图9 0.08 s时入射角15°和30°模型应力云图Fig.9 Stress cloud diagram of the model with an incident angle of 15°and 30°at 0.08 s

图10 入射角15°和30°底部中点和顶部中点位移时程图Fig.10 Time history diagram of the displacement of the bottom midpoint and the top midpoint at 15°and 30°incident angles
3 斜入射管廊的动力计算结果分析
斜入射地震作用下具有复杂的行波效应,结构在行波效应的作用下应变有所增大[22]。采用不同入射角度的方法以此来考虑行波的效应。将Kobe 地震波调整为0.1 g 并采用3 种入射角度由模型左下角输入进行对比分析,角度分别为0°、15°、30°,图11为3种不同入射角度下整体模型应力云图。
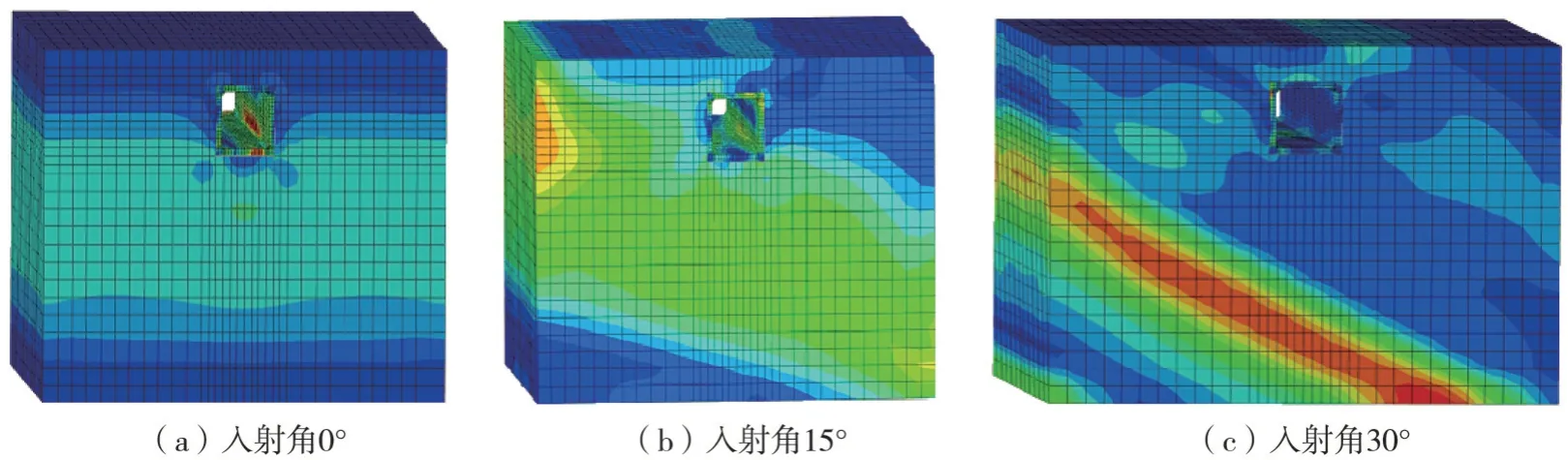
图11 3种不同入射角度地震力路径图Fig.11 Seismic force path diagrams under three different incident angle
分别对结构施加入射角为0°、15°、30°的地震波,测出管廊底部及土体底部加速度、侧壁相对水平位移、接头横向错动位移以及竖向接头位移。以下仅列出入射角为30°时的测量结果,图12为入射角为30°时的土体及管廊底部加速度时程曲线图,图13 为侧壁相对水平位移,图14 为管廊第一主应力与第三主应力云图,图15为接头的错动位移时程图。综合分析得出:

图12 入射角为30°地震作用下管廊底部及土体底部加速度时程曲线Fig.12 Acceleration time history curve of the bottom of the utility tunnels and the bottom of the soil under the earthquake action of an incident angle of 30°
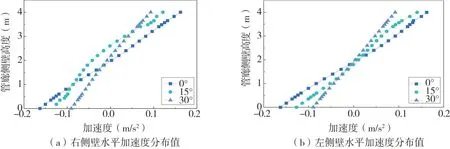
图13 管廊侧壁水平加速度分布值Fig.13 Horizontal acceleration distribution value of the side wall of the utility tunnels

图14 30°入射下第一主应力与第三主应力云图Fig.14 Contours of the first and the third principal stresses at 30°incidence

图15 30°入射地震波作用下接头错动位移时程图Fig.15 Time-history diagram of joint displacement under 30°incident seismic waves
(1)斜入射地震波输入时会分解为水平和竖向2 个分量。其中,入射角为30°时,水平加速度放大系数为1.01,竖向加速度放大系数为4.41;入射角为15°时放大系数分别为1.12和1.56;入射角为0°时放大系数分别为1.89 和0。可以发现,与垂直入射相比,由于反射折射复杂叠加的作用影响,土底加速度传播至结构底部会被放大,且随着入射角度的增加,水平加速度放大系数逐渐减小,而竖向加速度放大系数随着角度的增加逐渐增大,且放大系数明显大于水平加速度的放大系数。
(2)随着入射角度的增大,同一高度管廊侧壁水平加速度逐渐减小,管廊高度为0.5 m时,水平加速度由入射角为0°时的0.15 m/s2减小到15°时的0.1 m/s2再减小到30°时0.075 m/s2,大致以侧壁中点为正负加速度分界点,这也将造成结构顶底板相对水平位移的产生。
(3)在斜入射地震作用下,管廊结构依然在腋角四周应力分布较为集中。随着角度的增加,结构的第一主应力逐渐减小,第三主应力逐渐增大,造成该原因主要是因为竖向分量的增加及波发生反射折射叠加造成。其中在0°入射条件时第一主应力最大,为322 kPa,在30°入射条件时第三主应力最大,为-412 kPa。因为斜入射在竖向的作用上会比垂直入射方式来的大,这也是由于角度的增大引起竖向加速度放大导致的,需要引起一定的重视。
(4)随着入射角度的增大,结构接头间横向错动位移不断减小,竖向错动位移不断增大,入射角为0°、15°、30°时横向接头位移分别为0.37、0.25、0.22 mm;入射角为15°、30°竖向接头位移分别为0.25、0.28 mm。可以发现竖向位移的增大大于水平位移的减小,对接头的影响明显增大。
4 结论
(1)在对单元选择、土体动力本构、动力接触模拟和求解方法分析的基础上,建立了考虑土结共同作用的预制拼装综合管廊的动力分析有限元模型。通过分析斜入射的内行位移场及应力场,建立了考虑斜入射粘弹性边界,能够实现斜入射地震作用下预制拼装管廊的地震响应分析,基于Python 编程语言所编制的粘弹性人工边界及节点力自动施加程序Auto_VSB能够极大提高计算效率且具有很好的计算精度。
(2)与垂直入射相比,由于反射折射复杂叠加的作用影响,斜入射时土底加速度传播至结构底部会被放大,且随着入射角度的增加,水平加速度放大系数逐渐减小,而竖向加速度放大系数随着角度的增加逐渐增大,且放大系数明显大于水平加速度的放大系数。其中,入射角为30°时,水平加速度放大系数为1.01,竖向加速度放大系数为4.41。
(3)随着入射角度的增大,同一高度管廊侧壁水平加速度逐渐减小,大致以侧壁中点为正负加速度分界点,这是造成结构顶底板相对水平位移产生愿原因。
(4)随着入射角度的增大,结构接头间横向错动位移不断减小,竖向错动位移不断增大,可以发现竖向位移的增大大于水平位移的减小。说明,斜入射输入方式在竖向对结构造成较大影响,且总体变形明显大于水平入射,在实际工程中应加以考虑。
