二阶振型对场地地震变形及地下结构地震响应的影响

2022-07-21江志伟许成顺杜修力刘晶波

地震工程与工程振动 2022年3期

江志伟，许成顺，杜修力，刘晶波

（1.北京工业大学城市与工程安全减灾教育部重点实验室，北京 100124；2.北京城建设计发展集团股份有限公司城市轨道交通绿色与安全建造技术国家工程研究中心，北京 100037；3.清华大学土木工程系，北京 100084）

引言

通常认为在地震荷载作用下场地的响应主要呈现一阶振型，因此有诸多学者研究并发展了确定场地一阶频率与振型的简化分析方法［1－2］，相关研究成果已被用来确定场地地震设计反应谱，并已在地上结构的抗震设计中得到广泛应用。而对于地下结构，由于受周围岩土介质的约束，结构地震响应主要依赖于场地变形，结构惯性作用对其地震响应的影响较小，因此土体地震变形也为地下结构抗震分析中最主要的地震荷载。目前在地下结构抗震设计［3－4］和抗震性能推覆分析中［5－7］，主要还是借鉴地上结构的场地地震响应分析方法，也即采用场地的一阶振型作为其地震变形模式来近似获取结构对应位置处土体的等效地震变形。

但实际上地震荷载还可激发场地的高阶振型效应，甚至在一些特殊情况下场地还可产生共振响应，例如Ermert 等［8］通过原位测试识别了山谷场地高阶振型，其可能产生的共振响应可使局部范围内土体的地震变形显著增大。由于结构对土体变形极为敏感，若场地产生高阶振型响应，必然对地下结构的地震安全产生严重影响。然而，目前在抗震设计中尚未重视场地的高阶振型作用，这对正确分析地下结构地震响应和抗震性能评价具有不可忽略的影响。

作者依托北京地铁6 号线某实际工程，开展了装配式马蹄形隧道结构的1-g 大型振动台模型试验（简称“隧道试验”），在试验中模型隧道结构产生严重损伤并逐步演化为一个多铰机构［9］，这远超在试验前预期的地震响应结果。因试验中的模型土并不存在软弱和液化层，认为场地过大的剪切变形以及结构强烈的水平地震响应可能与场地高阶振型的参与有关。

因地下结构的地震响应受制于自由场土体的地震响应［10］，文中主要针对与隧道试验［9］同期开展的自由场场地1-g 振动台试验（简称“自由场试验”）［11］开展研究工作，主要目的是分析场地的高阶振型对其地震变形和埋置于土体内地下结构地震响应的影响。首先介绍土体在试验中的频率、振型与变形响应，在此基础上研究二阶振型对土层变形大小的贡献，最后采用整体式反应位移法［4，12］分析场地的二阶振型作用对马蹄形隧道结构地震响应的影响。

1 自由场振动台试验测试与激振方案

试验在6 m×6 m 振动台上开展，模型箱为叠层剪切箱，内壁布有1 cm 厚的橡胶膜。前文［11］已详细介绍了自由场试验的方案，本节主要对传感器布置和地震动激振方案进行简要介绍。

振动台和模型箱如图1（a）所示；试验共使用35个加速度传感器，如图1（b）所示。加速度传感器以CHn（n=01，02，…，05，09，10，…，35）命名并进行编号，其中CH01 布置在振动台台面上用来记录台面运动，CH02～CH05 和CH09～CH29 被埋置于土体中用来记录土体的地震响应，CH30～CH35 则被布置于模型箱上，用来记录箱体运动。

图1 模型箱与传感器布置［11］Fig.1 Arrangement of soil container and sensor［11］（Unit：m）

试验共输入1 条场址人工地震动和3 条天然地震动，分别为北京人工地震动、Kobe（1995日本）、Loma Prieta（1989 美国）和Wenchuan（2008 中国）地震记录。对地震动的频谱进行了缩放，原则是激发试验体系最不利的地震响应［11］。综合考虑，确定北京（BJ）人工地震动、Kobe、Loma Prieta（LP）和汶川（WC）记录的频谱缩尺比（原型/模型）分别为1/2、1/5、1/2 和1/5。试验按地震动峰值加速度的不同分为4 个加载阶段，分别为0.2、0.4、0.62、1.0 g阶段，地震动输入顺序详见表1。

表1 动力荷载输入顺序［11］Table 1 Input motion sequence［11］

2 场地的振型及其对土体变形响应的影响

为分析场地的二阶振型效应对地下结构地震响应的影响，首先须明晰自由场土体的地震变形并识别二阶振型，本节主要对试验中自由场土体的频率、振型和变形大小开展分析。

2.1 场地的卓越频率与振型

由土体在白噪声荷载下的响应可获取土体在任意测点位置处的传递函数，其中在CH15 和CH07 处的传递函数如图2 所示（工况IM－1）。由2 个传递函数可知，体系的一阶和二阶自振频率别为9.1 Hz 和28.8 Hz。但由传递函数较难识别土体的三阶及以上频率，这是因为振动台的额定工作频率仅为0.1～50 Hz，而土体的三阶及以上自振频率可能大于50 Hz。

由图2 可知，2 个不同传感器所得到的传递函数在一阶和二阶频率位置处对应的大小不同。由CH01～CH15处的传递函数（复数）实部沿高度方向的分布可获取自由场土体的一阶振型［13］，同理可获取土体的二阶振型，将2个振型做归一化处理［14］后如图3所示。由一阶振型可知，其沿高度的方向近似呈斜直线，这表明自由场土体在初始状态下并无软弱层，与试验实际场地情况相符。一阶振型坐标沿高度方向逐渐增大，在CH15位置处达到幅值；而二阶振型坐标则先增大后减小，其拐点位于CH06～CH09范围内，振型幅值位于CH08位置处。

图2 自由场土体在白噪声荷载（IM－1）下的传递函数Fig.2 Transfer functions of free-field soil under white noise motions（IM－1）

此外，在装配式马蹄形隧道结构振动台模型试验中［9］，使用的模型土、模型箱和传感器布置方案与自由场试验中的一致，模型结构约位于图1（b）中的CH08～CH06位置处，关于试验的详细介绍请见Xu等［9］。在隧道试验中也可由白噪声获取土体的传递函数与振型，其中一阶和二阶振型如图3所示，对比由自由场和隧道试验获取的振型结果可知，二者的差异不大。可见2组试验的振型结果可以互相印证，获取的自由场试验振型结果合理，可在后续分析中使用。

2.2 场地的水平剪切变形

由自由场土体在地震荷载作用下的加速度响应，可获取土体在各个高度位置处的积分位移。获取积分位移时，采用带通滤波器对加速度时程进行滤波，滤波器带宽为0.5～40 Hz。

通常认为自由场土体在地震荷载作用下的变形模式主要呈一阶振型，由图3可知，土体的一阶振型近似为一直线，若土体仅按一阶振型运动，其在任意2个相同高度范围内水平变形的差异应很小。

图3 场地土在振动台试验中的振型Fig.3 Mode shapes of soil in shaking table tests

由土体的积分位移结果可获取在CH15～CH09和CH09～CH05这2个范围内等厚土层的峰值水平剪切变形（dF1和dF2），详见表2。对比dF1和dF2可知，在绝大部分工况作用下，dF2均大于dF1，即土体中部的变形比上部土体的大，且在部分工况作用下二者的差异悬殊。例如在工况IM-4 时，dF1为－0.11 cm，而dF2可达－0.20 cm，dF2约为dF1的181%。由此可知，试验中土体的变形模式与传统认识存在较大差异。

此外，可通过隧道试验［9］获取场地土在CH29～CH27 和CH27～CH25 这2 个对应范围内等厚土层的峰值相对位移（dT1和dT2），如表2 所示。对比dT1和dT2可知，在绝大部分工况作用下dT2也均大于dT1，这与在自由场试验中得到的规律基本一致。由此可知，在2 组试验中，土体的变形均在中部位置处得到了放大或缩小，这与二阶振型的幅值和拐点位置较为接近，文中认为土体局部变形的放大或缩小与体系二阶振型的参与有关。

表2 2组试验中的土层变形结果Table 2 Soil deformation in two groups of experiments cm

2.3 二阶振型对土体剪切变形的贡献

为分析振型对土体变形模式的影响，首先需分析土体在试验中的变形模式。假设自由场土体在工况IM－4 时产生dF2的时刻为t1，可得土体在t1时刻沿高度方向的归一化变形模式ϕ，如图4（a）所示，对比其与场地一阶振型ϕ1和二阶振型ϕ2可知，场地变形模式与一阶振型ϕ较为接近，这与传统认识相近。但对比ϕ和ϕ1可知，二者仍然存在一定的差异，土体的一阶振型ϕ1难以完全代表其在地震荷载中真实的变形模式。

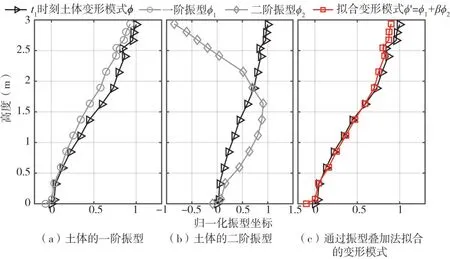
图4 土体的振型与在t1时刻的变形模式（工况IM－4）（β=11%）Fig.4 Mode shape and deformation mode of soil at t1（IM－4）（β=11%）

因0.2 g阶段加载时土体的非线性响应较小，可近似采用“振型叠加法”对场地地震响应进行分析。将土体简化为了弹簧－质点模型，模型沿高度方向的位移向量u可近似由式（1）获取［14］：

式中，q1和q2分别为一阶和二阶振型的参与系数。

因一阶振型对土体的地震响应起主导作用，为更加直观地对比二阶振型与位移向量u之间的关系，对式（1）做如下变换：

式中，β=q2/q1，代表了二阶振型在试验中的参与程度。

对u′进行归一化处理后，可得由前两阶振型构造的土体变形模式ϕ′。采用调整系数β的方法使ϕ′拟合试验实测土体变形模式ϕ，其结果如图4（c）所示，此时β等于11%。可知，当二阶振型参与到土体的变形模式中后，拟合结果逼近了土体真实的变形模式，这表明二阶振型参与到了土体的地震响应中。值得注意的是，尽管考虑场地的二阶振型后，拟合后的场地变形模式仍与真实变形模型存在一定差异，这可能是因为拟合过程中仅考虑了前两阶振型，而未考虑三阶及以上振型的贡献所致。

在后续0.4 g至1.0 g阶段，场地的非线性响应较强，此时叠加原理已不再成立。但这里仍采用类似的方法对场地地震响应开展定性分析，其结果仅供参考，如图5和图6所示，图中的t2和t3时刻分别为工况IM-9和工况IM-17产生dF2的时刻。

由图5 和图6 可知，与0.2 g 阶段的场地变形模式相比，强震作用下当二阶振型参与至场地变形后，拟合与真实变形模式差异变大，也即由振型叠加法得到的拟合精度下降，这可能与场地的强非线性响应有关。尽管如此，二阶振型参与后的场地变形模式仍趋近于土体真实的变形模式，这与在0.2 g阶段得到的规律（图4）相近，可见尽管场地产生了强非线性响应，但其并未从本质上改变场地的地震响应规律。因此仍采用拟合的方法获取土体在所有工况作用下二阶振型参与系数β，以定性地分析二阶振型参与系数的大小，如表2所示（表中0.4 g～1.0 g阶段的β仅供参考）。由表2可知，无论地震动峰值加速度大小如何，二阶振型参与系数β均较小，在－10%～20%以内变化，这表明地震作用下的场地变形仍主要以一阶振型为主，二阶振型的参与程度有限。

图5 土体的振型与在t2时刻的变形模式（工况IM－9）（β=14%）Fig.5 Mode shape and deformation mode of soil at t2（IM－9）（β=14%）

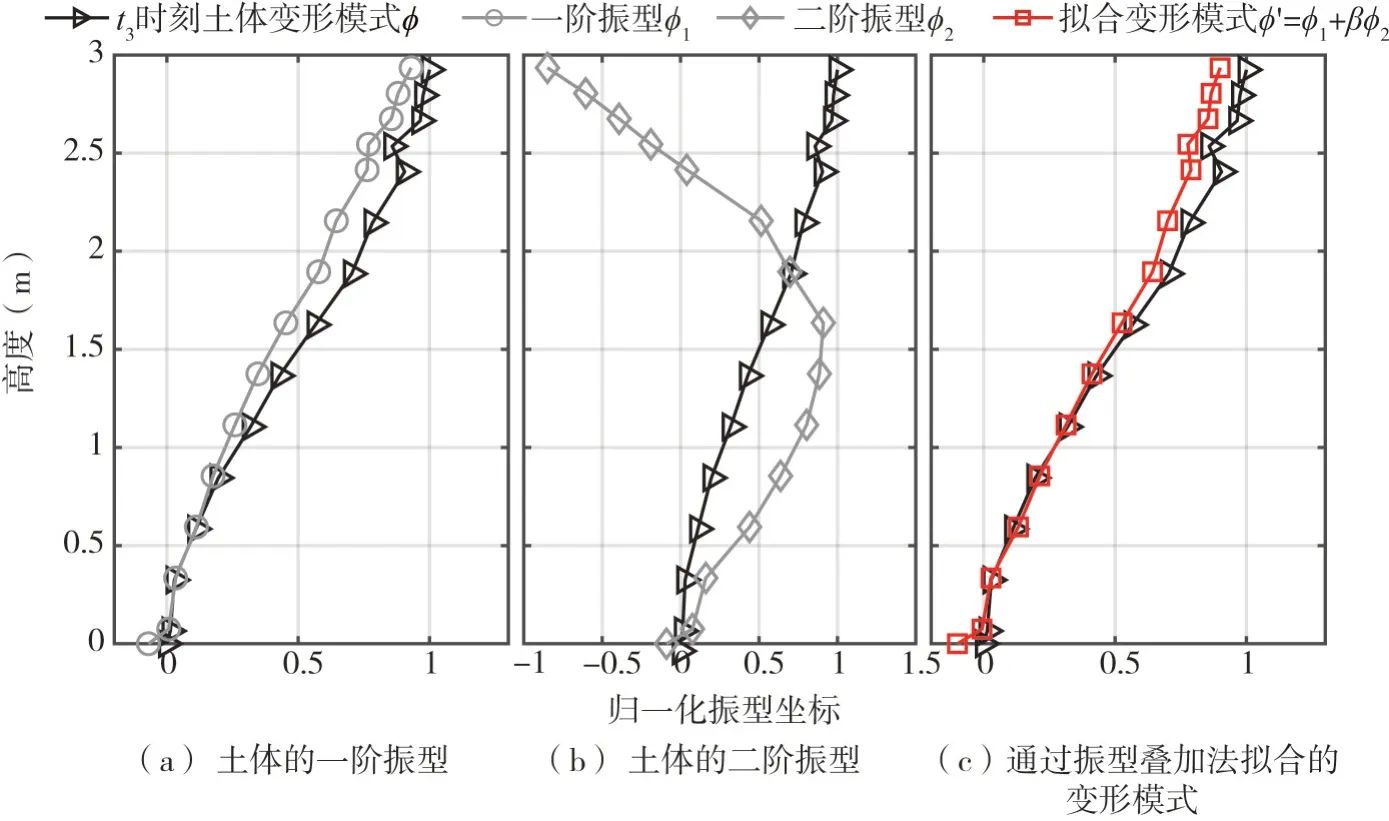
图6 土体的振型与在t3时刻的变形模式（工况IM－17）（β=7%）Fig.6 Mode shape and deformation mode of soil at t3（IM－17）（β=7%）

为分析二阶振型对场地地震响应的影响，可分析在不同二阶振型参与系数β情况下土层的变形。因小震时ϕ′可近似代表土体的变形模式，即ϕ′≈ϕ，而ϕ为土体变形的归一化结果，因此可近似通过基底－地表相对位移对ϕ′进行调幅，以获取小震时土体在CH15～CH09 和CH09～CH06 范围内的等效相对位移dF1′和dF2′。当β在－10%～20%间变化时，dF1′和dF2′的结果如表3所示。

表3 土层在不同二阶振型参与系数下的相对位移对比Table 3 Relative displacement of soil with different 2nd mode participation coefficients cm

分析β与土体的剪切变形大小可知，当β=0，即未有二阶振型参与时，中部土体变形dF2′略大于上部土体变形dF1′，但二者的差异很小。当β<0时，上部土体变形dF1′增大，大于下部土体变形dF2′，可见二阶振型的参与可能使中部土体变形减小；而当β>0时，土体中部变形dF2′随着β的增大而增大，土体变形逐渐在中部位置处集中，远大于上部土体变形大小。例如，在工况IM-11 作用下，当β为15%时，dF1′为0.47 cm，而dF2′可达1.58 cm，这与在自由场和隧道试验中观测到的规律类似。由此可知，二阶振型的参与是导致试验中土体中部变形增大或减小的主要原因。从另一个角度看，二阶振型的参与改变了场地局部的剪切变形分布模式。

3 场地的二阶振型对地下结构地震响应的影响

因二阶振型作用可增大或减小局部土体的变形响应，若有地下结构埋置于此范围内，结构的地震响应必然受到影响，本节通过有限元数值分析对场地的二阶振型作用对地下结构地震响应的影响开展分析。

3.1 计算模型与参数

采用整体式反应位移法［4，12］对埋置于自由场土体内的隧道结构开展地震响应分析，因结构惯性力作用的影响很小［15］，计算主要考虑了土层变形的影响，需获取土体的动剪切模量比和结构位置处土体的剪切变形。

为获取土体的动剪切模量比，须首先估算土体的最大剪切模量Gmax，试验中砂土的Gmax可采用式（3）估算：

式中：e为土体的孔隙比；σ0为土体的有效围压；C为常数，约为0.47［16］。

其中土体的围压可由其竖向压力和侧向压力K0系数获取，竖向压力可由任意土体高度和土体的重度γt获取，K0则可由式（4）估算［17］：

将自由场土体简化为一维弹簧－集中质量模型，各质点的坐标与加速度传感器CH01～CH15 的竖向高度一致，可由不同高度处土体的Gmax和初始重度γt建立模型的刚度和质量矩阵，可进一步通过解析法获取体系的一阶和二阶频率，分别为9.9 Hz和26.0 Hz。对比其与图2中由传递函数获取的频率结果可知，二者差异较小，这表明采用式（3）估算的Gmax结果较好。

动剪切模量比G/Gmax可采用Menq 模型［18］估算，其已被广泛应用至一维非线性场地分析中［19］。Menq 模型可用式（5）表示：

式中γr和a分别为砂土的参考剪应变和曲线调整系数，可通过Cu和σ0获取，详见Menq［18］。

假设初始工况IM－3 作用下，模型结构恰好埋置于自由场土体的CH08～CH06 位置处，为采用Menq 模型获取土体的动剪切模量比G/Gmax，首先须获取土体的动剪应变γ。令CH08～CH06 位置处土体产生最大剪切变形的时刻为t2，因此时土体的非线性程度较小，其变形模式可近似采用振型叠加法获取。对土体的位移采用试验中实测的基底－地表相对位移进行调幅，则可采用图4（c）中的方法近似构造出土体在t2时刻沿高度方向的变形，其中当二阶振型参与系数β为20%时土体的变形如图7所示。

图7 土体在二阶振型参与情况下沿高度方向的位移分布（工况IM－3）Fig.7 Deformation of soil along the elevation with participant of 2nd mode shape（IM－3）

由土体变形可获取其在t2时刻任意高度处的剪应变γ，进而可通过Menq［18］模型和Gmax获取相应的动剪切模量G。同理可获取当β为－10～20%范围内变化时结构对应位置处土体的相对位移、动剪应变γ和动剪切模量G，如表4所示。

由表4可知，随着β的增大，结构位置周围土体的水平相对位移逐渐增大，导致土体剪应变γ增大和动剪切模量G减小，可见二阶振型的参与改变了地下结构所受的荷载与边界条件。

表4 不同二阶振型参与系数β所对应结构位置处（CH08～CH06）土体的计算参数Table 4 Parameters for numerical analysis of soil at structural position（CH08～CH06）with different 2nd mode participation coefficient β

按照规范［4］中的方法，在有限元软件ABAQUS 平台上开展模型隧道结构的地震响应计算，有限元数值模型如图8所示，其中土体和结构分别采用二维平面应变和梁单元建模。隧道结构为马蹄形断面，最大水平和竖向尺寸均约为0.52 m，径向厚度为0.026 m，隧道衬砌为线弹性模型，弹性模量为13.8 GPa［9］。将土按图1（a）中的传感器位置划分为14 层，并对各土层分别赋予t2时刻求得的动剪切模量G。土与结构绑定，不考虑二者的相对滑移。

图8 整体式反应位移法有限元计算模型Fig.8 Finite element model of integral response deformation method

3.2 隧道结构地震响应分析

隧道结构的地震响应结果如表5 所示。由表5 可知，当β=0时，即当二阶振型未参与到场地的地震变形中时，隧道结构顶端和底端间的水平相对位移为－0.245 mm；当β<0 时，隧道结的顶－底水平相对变形逐渐减小，结构趋于安全。而当β>0 时，即二阶振型参与到场地的地震变形中时，结构的顶－底水平相对变形逐渐增大，当β增大至20%时，其大小约为－0.409 mm，相对于β=0时增大了66.5%。