水平及竖向地震下的钢筋混凝土框架混合试验方法

2022-07-21郭玉荣朱钊利

地震工程与工程振动 2022年3期

郭玉荣，朱钊利

（1.湖南大学土木工程学院，湖南长沙 410082；2.建筑安全与节能教育部重点实验室，湖南长沙 410082）

引言

已有的地震记录表明，近场地震会出现较为显著的竖向地面加速度，竖向地震对结构的破坏不可忽视。早在20世纪70年代，钱培风［1］就从近场地震震害现象中发现了竖向地震对结构的破坏作用。周正华等［2］以国内外数十次近场地震的地面加速度记录为基础进行分析，结果表明在近场区竖向地震效应显著。在水平和竖向地震的同时作用下，框架结构中柱子轴力的大幅持续变化会对柱的承载力、刚度和滞回性能等产生显著的影响，从而影响框架结构的地震响应。混合试验方法为模拟结构地震响应提供了一种新型有效的手段，但以往的建筑结构混合试验方法大多只考虑水平地震作用或多维地震加载仅应用于验证性的简单结构案例。研发多高层钢筋混凝土框架结构在水平及竖向双向地震作用下的混合试验方法，可以进一步拓展混合试验方法的应用。

混合试验［3］源于拟动力试验，其将完整的结构分为试验子结构和数值子结构两部分，试验子结构是将地震作用下容易破坏的强非线性部分进行加载试验，而数值子结构是将其余部分进行计算模拟。近年来，不少学者对混合试验方法进行了研究并开发了相应的试验平台或软件，如OpenFresco［4］、UI-SimCor［5］、Net‐SLab［6］、P2P 分布式混合试验平台［7］、HyTest［8］、MTS-OpenFresco-MATLAB 混合试验系统［9］等。在使用这些平台或软件进行结构混合试验时，由于试验设备和加载条件的限制，往往只进行结构在水平地震激励下的混合试验，如范云蕾等［10］采用2 个水平作动器对一榀十层三跨钢管混凝土组合框架结构进行了子结构拟动力试验，郭玉荣等［11］采用一个水平作动器对一榀十层三跨BRB 组合框架进行了混合试验，王贞等［12］采用4 个水平作动器对6层预制钢筋混凝土剪力墙盒子结构进行了混合试验，蔡新江等［9］采用1个水平作动器完成了一榀两层单跨钢框架的混合试验，张琦等［13］用4 个水平作动器对一个局部单层的三层多跨偏心支撑组合钢框架结构进行了远程协同混合试验。此外，哈尔滨工业大学吴斌教授课题组［8，14］在进行水平地震激励下的单层单跨钢框架混合试验中，采用3 个MTS 作动器完成试验子结构柱顶边界3 个自由度的协调控制位移加载，为多维加载控制的结构混合试验提供了设备技术支持。在多向地震同时激励的结构混合试验研究方面，钟树生［15］利用杆系模型编制了水平及竖向地震联合作用的混合试验程序，并进行了两层一跨钢筋混凝土框架的混合试验；袁志仁［16］提出了基于修正的OS法的水平及竖向地震混合试验方法，同样进行了两层一跨钢筋混凝土框架的混合试验。但是总的来说，水平和竖向地震激励下的结构混合试验方法研究还比较有限，存在数值子结构模拟效果差、时程分析计算精度低等问题。

近年来，作者所在单位建设了大型多功能加载设备MUST，4 个竖向布置的作动器合计可施加2 000 t的力，2个水平作动器合计可施加400 t的力，为实现水平和竖向地震同时激励下的混合试验提供了设备支持。结合该设备，文中研发一种多高层框架结构在水平和竖向地震共同作用下的混合试验方法，采用Matlab 编写整体结构运动方程求解模块，并连接通用结构有限元分析软件OpenSees求解数值子结构的恢复力来编制结构混合试验程序。以一榀七层三跨框架为例，通过对比分析混合试验的误差大小和误差来源来验证文中方法的可行性和有效性。

1 水平和竖向地震下的混合试验基本流程

结构混合试验主要包含3 个核心内容：（1）试验子结构，该部分为真实构件在实验室中进行加载试验；（2）数值子结构，该部分利用计算机建模模拟；（3）整体结构运动方程的建立与求解。

在进行框架结构的混合试验时，一般取受力较为复杂的柱子为试验子结构。水平地震作用下框架结构的倾覆力矩变化会引起柱子的轴力变化，但是这种轴力变化幅度相对较小。在竖向地震作用下，柱子的轴力持续发生变化且变化幅度较大。高水平、大幅度的轴力变化会显著影响柱子的抗弯承载力、刚度和滞回性能等特征，从而对框架结构的地震响应产生较大影响。因此，当进行水平和竖向地震同时激励下的框架结构混合试验时，从框架结构中取出柱子为试验子结构进行试验加载，需要试验设备具有变轴力的加载能力，如图1所示。

对于图1 中的数值子结构，需要对柱子的非线性滞回性能进行数值模拟。以往的混合试验常常采用经验的恢复力模型来计算构件的恢复力，当考虑轴力变化对柱子的滞回性能产生影响时，则恢复力模型参数也需要相应的修正，这种模拟方法编写程序非常复杂。即使采用这样的方法，依旧不能很好地模拟轴力变化下的柱子受力性能。为了更真实地获取每一积分步下的柱子恢复力，利用OpenSees 构建数值子结构的纤维模型，纤维模型能对构件的受力状态进行较好的模拟。利用位移加载的方式，在每一积分步数值子结构加载水平和竖向预测位移，并返回预测位移下的结构内力。

图1 混合试验示意图Fig.1 Schematic diagram of hybrid simulation

为了实现水平和竖向地震下的混合试验，需要建立框架结构的整体运动方程。结合楼板平面内无限刚性的假定建立水平运动方程，楼板平面外有限刚度假定建立竖向运动方程。采用Matlab 编写程序建立运动方程，同时利用数值积分方法进行时程分析，计算每一积分步上的结构运动状态。

水平和竖向双向混合试验的基本流程如下：

步骤1：已知第i－1 步的位移、速度加速度。利用PC－Newmark 法分别计算第i步的水平预测位移和预测速度、竖向预测位移和预测速度。并将水平和竖向预测位移发送给数值子结构和试验子结构。

步骤2：OpenSees 中的数值子结构利用预测位移进行各节点的加载，并获得相应的内力以及对应的恢复力。

步骤3：试验子结构柱利用对应的预测位移进行加载，并获得剪力和轴力。

步骤4：Matlab 中整合获得的恢复力形成水平恢复力列向量和竖向恢复力列向量。利用恢复力列向量计算水平、竖向加速度，同时修正水平、竖向位移和速度。

步骤5：重复1～4 的过程，直至试验结束。

具体的混合试验流程如图2所示。

图2 水平和竖向地震下混合试验流程图Fig.2 Flow chart of hybrid simulation under horizontal and vertical earthquakes

2 水平和竖向地震下混合试验的关键问题

2.1 边界条件的处理

混合试验的关键问题之一是边界条件的控制，数值子结构和试验子结构之间边界条件的协调会影响混合试验的精度和效果。对于二维平面框架，梁柱节点一共有3个自由度，也就意味着物理子结构和数值子结构之间的边界条件需要保持3 个自由度的协调。试验子结构的边界条件一般由作动器实现，但是大多数的实验室因设备条件限制无法做到同时控制柱顶的3个自由度，往往忽略转动自由度，只控制水平和竖向自由度的位移。因此，结合MUST设备加载能力，文中的混合试验方法也只控制柱顶的水平和竖向自由度。对于水平和竖向自由度，采用位移控制的方法，在混合试验的过程中保证数值子结构和试验子结构边界的水平和竖向位移一致。

2.2 结构振动模型

确定时程分析的结构振动模型是混合试验的关键步骤，实际中通常会将平面框架的质量集中在各个梁柱节点，同时考虑各个节点的水平、竖向和转动自由度。节点转动自由度的计算存在一定困难，同时由于试验设备的限制，选择忽略结构节点的转动自由度。当选取的框架结构的梁柱线刚度比足够大时，节点近似不发生转动，不考虑转动自由度所带来的误差可以忽略不计。忽略节点的转动自由度时，可以缩减结构的动力自由度。根据刘季［17］的推导，当水平和竖向地震同时作用时，竖向振动是独立的，竖向振动的运动方程如式（1）：

式中：M为质量矩阵；CV为结构竖向阻尼矩阵；KV为结构竖向刚度矩阵；Y为竖向位移列向量；I为单位列向量。

水平和竖向地震同时作用时，结构的水平振动和竖向振动耦合，其水平振动的运动方程如式（2）：

式中：CH为结构水平阻尼矩阵；KH为结构水平刚度矩阵；KG为几何刚度矩阵；X为水平位移列向量。

当不考虑结构的几何非线性时，方程（2）中的KG= 0，则水平与竖向振动不耦合。因此，不考虑水平和竖向运动的耦合性，即水平和竖向运动分别独立计算。

通常假定楼板平面内的刚度无穷大，在水平地震作用下，同一层的水平位移是相等的。因此可以将同一层的质量集中在一起，形成串联质点系模型，即层剪模型。而在竖向地震下，楼板的平面外刚度很小，并且梁的刚度也是有限的，同一层楼的竖向位移不能近似相等。因此，在竖向地震作用下的结构竖向运动计算不能采用串联质点系模型，需要采用串并联多质点系模型［18］，水平和竖向振动模型如图3所示。

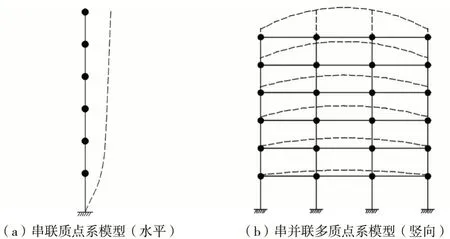
图3 水平和竖向振动模型Fig.3 Horizontal and vertical vibration models

2.3 水平和竖向运动方程

在地震作用下结构会进入弹塑性状态，运动方程中的恢复力项无法用恒定的刚度表示。同时，由于结构在竖向受到初始静力作用，在运动方程中必须考虑这部分静力作用的影响。

由于水平和竖向运动分别独立计算，在水平和竖向地震作用下结构的竖向运动方程和水平运动方程如式（3）和式（4）所示：

式中：fV为结构的竖向恢复力列向量；fH为结构的水平恢复力列向量；Pg结构初始竖向荷载列向量。

建立运动方程时，需要获取结构的阻尼矩阵，文中方法采用Rayleigh阻尼。Rayleigh阻尼的构造如式（5）所示：

对于竖向和水平的阻尼矩阵，分别采用对应的质量和刚度矩阵。

2.4 混合试验时程分析的数值积分方法

混合试验的核心是对结构进行地震作用下的时程分析，时程分析常常采用数值积分方法。文中采用PC-Newmark 法进行时程分析。PC-Newmark 法又被称作预测－校正Newmark 法，其拥有较好的稳定性和较高的计算精度，预测及校正的过程适用于混合试验。

PC-Newmark法把一个数值积分步的计算分为预测和校正2部分。预测部分公式如（6）和（7）所示：

式中：为第i+1 步的预测位移和预测速度列向量；di、vi和ai为第i步的位移、速度和加速度列向量；β、γ为数值积分算法参数，可取β=0.25，γ=0.5。

校正部分公式如式（8）～式（10）所示：

式中：ai+1为i+1 步的加速度列向量；为预测位移作用在结构上获得恢复力列向量；ag,i+1为第i+1 步的地面加速度；di+1为结构校正位移列向量；vi+1为结构校正速度列向量。

3 混合试验数值模拟

以一榀七层三跨的钢筋混凝土框架为例，通过对比虚拟混合试验和单独用OpenSees进行时程分析来验证文中所提出方法的可行性和有效性。

3.1 数值模拟模型概况

所选取的一榀七层三跨框架如图4 所示。该框架底层层高为3.7 m，其余层层高为3.0 m，跨度6.0 m，柱和梁截面分别为600 mm×600 mm 和600 mm×1 400 mm。框架结构梁上的分布荷载为39 kN/m，边节点集中荷载为198.75 kN，中节点集中荷载为240 kN。框架边节点质量为32.22 t，中节点质量为48.37 t。地震波选取El Centro 波的水平和竖直分量，水平向的峰值加速度调整为0.9 g，竖向的峰值加速度调整为水平向的2/3。整体时程分析的持时为15 s。

图4 框架结构分析模型Fig.4 Analysis model of frame structure

取底层中柱作为试验子结构，为了使混合试验中数值子结构和试验子结构之间的边界条件相近，将试验子结构的柱顶转动进行约束。

本节算例选取框架结构的梁柱线刚度比较大，其主要有以下2 点考虑：（1）文中混合试验方法忽略节点的转动约束，为了减小其带来的误差，本节选取梁柱线刚度比较大的框架；（2）混合试验的一个重要误差来源为子结构之间边界条件的不一致。为了减小这部分误差，选取梁柱线刚度较大的框架，同时对试验子结构柱顶的转动进行约束。

3.2 弹性框架虚拟混合试验

首先假设该框架为弹性框架，所有梁柱采用弹性单元，弹性模量E取为3 × 104MPa。利用OpenSees 模拟试验子结构，同时结合混合试验程序进行虚拟混合试验。单独采用OpenSees 对完整框架结构建模并进行时程分析，其时程分析结果作为参考解与虚拟混合试验进行对比验证。

虚拟混合试验和纯OpenSees 时程分析的结构底层中柱位移、内力响应如图5 所示。为了定量分析两者差异，计算虚拟混合试验与纯OpenSees 时程分析的误差列于表1，误差参考标准取为底层中柱柱顶内力和位移的平均绝对误差（MAE）和相关系数（r）。MAE值和r值的计算公式如式（11）和式（12）所示：

表1 柱顶位移、内力时程对比的MAE值和r值Table 1 MAE and r value of comparison of displacement and internal force at top of column

图5 柱顶位移、内力时程曲线Fig.5 Time history curve of displacement and internal force at top of column

式中：xi,ref、xi分别为真实值和对比值；Xref、X分别为真实值和对比值的向量；Cov(X,Xref)为真实值和对比值的协方差；Var|Xref|、Var|X|分别为真实值和对比值的方差，n为数据点的数目。

从图5可以看出，虚拟混合试验和纯OpenSees时程分析的底层中柱内力和位移时程曲线比较吻合，表1中的MAE值和r值表明二者差异较小。分析其中误差的主要来源为：

（1）数值积分方法的不同。文中混合试验方法采用PC-Newmark法，而OpenSees时程分析采用Newmark-β法，Newmark-β法难以用于混合试验。虽然2 种数值积分方法类似，但仍存在不同，并导致时程分析结果存在差异。

（2）节点转动自由度的忽略。文中混合试验方法忽略了节点转动自由度，该简化会对时程分析结果造成误差。本节模拟采用梁柱线刚度比较大的框架，若梁柱线刚度比增大，则误差会相应地减小。

（3）子结构边界条件的不一致。文中混合试验方法采用不完整边界条件，其无需控制试验子结构的转动边界条件。这样的方法满足大多数实验室的试验设备条件，同时也产生了误差。本节模拟采用梁柱线刚度比较大的框架，同时对试验子结构柱顶的转动进行约束，这样的处理能保证子结构之间的边界条件相近并减小误差。

从弹性框架混合试验较小的误差可见，当梁柱线刚度比较大时，数值积分方法、节点转动自由度和子结构边界条件这些误差来源并不会造成较大的误差。

3.3 钢筋混凝土框架虚拟混合试验

将弹性框架改为钢筋混凝土框架，所有梁柱采用基于力插值函数的非线性梁柱单元，每个单元选取5个高斯积分点。梁柱截面为纤维截面，混凝土纤维的本构模型为Concrete01 模型，即改进的Kent-Scott-Park 模型。钢筋纤维的本构模型为Steel01 模型，即单轴双折线模型。柱截面配筋图如图6 所示，钢筋和混凝土本构模型参数见表2。

图6 柱截面配筋图Fig.6 Reinforcement diagram of column section

表2 Concrete01、Steel01材料本构模型参数Table 2 Material constitutive model parameters of Concrete01 and Steel01

同样利用OpenSees模拟试验子结构以进行虚拟混合试验，将纯OpenSees时程分析作为参考解与虚拟混合试验进行对比。

虚拟混合试验和纯OpenSees时程分析的结构底层中柱位移、内力时程曲线如图7所示，平均绝对误差MAE值和相关系数r值如表3所示，时程曲线峰值对比如表4。试验子结构的水平滞回曲线与参考解的对比见图8。

表3 柱顶位移、内力时程对比的MAE值和r值Table 3 MAE and r of comparison of displacement and internal force at top of column

从图7 以及表3 的数据中可以看出试验子结构的时程曲线与参考解存在一定差异，但时程曲线趋势较为吻合，数值相差不大。从表3 和表4 可以发现，整体的平均绝对误差MAE值较小，相关系数r值较为接近1，时程曲线峰值相差不大。从图8可以看出，2种情况下柱子的滞回曲线较为接近。

图8 子结构柱滞回曲线与参考解的对比Fig.8 Comparison of hysteresis curve of substructure column and reference solution

表4 柱顶位移、内力时程的峰值对比Table 4 The comparison of peak displacement and internal force at top of column

图7 柱顶位移、内力时程曲线Fig.7 Time history curve of displacement and internal force at top of column

图7 （续）Fig.7 （Continued）

对于钢筋混凝土框架而言，虚拟混合试验结果与参考解的误差来源同弹性框架基本类似，即数值积分方法、节点转动自由度和子结构边界条件。除此之外，钢筋混凝土框架的第4点误差来源为阻尼的不同。虽然OpenSees时程分析和文中混合试验方法同样采用Rayleigh阻尼，但2种模拟所构造的Rayleigh阻尼矩阵有一定差别。Rayleigh 阻尼矩阵的构造需要结构的刚度矩阵，而结构刚度矩阵的构造需要各个构件的刚度。在构造阻尼矩阵时，文中方法采用混凝土构件的经验刚度以构造结构刚度矩阵，而OpenSees 时程分析对构件的纤维截面进行分析从而获得结构的刚度矩阵，两者的差别导致了阻尼矩阵的差异。

进一步分析得出，钢筋混凝土框架混合试验相对较大的误差主要来源为阻尼矩阵的不同。虽然钢筋混凝土框架混合试验与真实解相比存在一定误差，但其时程曲线趋势与真实解较为吻合，同时误差指标MAE相对于峰值较小。因此，文中的混合试验方法可以用于真实的混合试验。