基于Kanai-Tajimi谱卷积型非粘滞阻尼多自由度结构地震动响应的简明闭式解

2022-07-21李创第贺王涛葛新广

地震工程与工程振动 2022年3期

李创第，贺王涛，葛新广，2

（1.广西科技大学土木建筑工程学院，广西柳州 545006；2.柳州工学院土木建筑工程学院，广西柳州 545616）

引言

当下地震灾害所带来的人员伤亡和财产损失极大，防震减灾［1－2］研究成为当下重要的研究课题。阻尼［3－4］常被用来描述结构在振动过程中能量耗散的关键参数，其作用机理较为复杂，故仍没有统一阻尼模型。工程上应用较为广泛的粘弹性阻尼模型，未考虑振动滞后现象，与实际不符。为此，Biot［5］首先提出考虑滞后效应的非粘滞阻尼模型，阻尼力在数学形式上表现为质点振动速度同某一核函数的卷积。关于非粘滞阻尼结构体系的动力学分析，主要包含参数识别、模态分析和动力响应分析，其均得到广泛研究。但目前非粘滞阻尼结构的动力响应分析基本局限于确定性时程激励分析，关于非粘滞阻尼结构体系的随机响应分析研究报道较少。段忠东等［6］利用拉普拉斯变换对非粘滞阻尼模型阻尼参数识别进行研究，表明非粘滞阻尼模型在描述结构耗能更具有一般性。Liu［7－8］对指数型核函数型非粘滞阻尼结构的动力响应分析进行研究，指出非粘滞阻尼特征是许多工程结构地震中的耗能形式，并研究了时程激励下的结构地震动响应。汪梦甫等［9］利用指数型非粘滞阻尼体系地震反应的振型分解方法，对地震作用下的动力反应进行分析，并推导新的地震作用计算公式。吕蒙等［10］对卷积型非粘滞阻尼耗能系统风振响应特征进行了分析，利用微分求积算法，给出一种新的求解方法。

大量研究表明地震动具有显著的随机性且较为复杂，其中Kanai-Tajimi 谱激励模型［11－12］能考虑场地的动力特征对于地震动的影响，有着广泛的理论研究应用。研究结构随机地震动响应方法主要有频域法和时域法［13－14］2类。从频域角度分析，虚拟激励法［14－15］和传递函数法［16－17］需要获得结构地震动响应的方差等参数，上述方法分析0～2 阶响应谱矩时需要对结构响应的功率谱在频域内进行数值积分，但对于复杂的地震动激励模型或者大型复杂结构的响应谱矩计算仍较为繁琐［18－19］。从时域角度分析，复模态法为其典型方法［13，20－22］，其将线性振动体系进行复模态解耦，将动力响应协方差表示成脉冲函数与激励协方差的二重积分，因而获得响应协方差的前提需要给出其激励协方差。目前基于时域法的随机地震动响应表达式较为复杂［19－20］，不利于实际工程应用。

针对以上非粘滞阻尼结构随机地震响应分析不足、频域法积分计算相对繁琐等问题。首先，利用Kanai-Tajimi谱的滤波振动方程将复杂的地面运动表示成基于白噪声的随机地震动；其次，将指数型非粘滞阻尼结构积分型的本构关系转换成等效的微分型本构关系，联立Kanai-Tajimi 谱的滤波振动方程及微分型的非粘滞阻尼本构关系，给出了结构地震动基于白噪声激励的新的一阶状态微分方程组，利用复模态法解耦，给出了结构方差、功率谱和0～2阶谱矩的简明封闭解。

1 非粘滞阻尼结构地震动方程重构

结构计算简图如图1所示，该结构为l层的线性结构，结构动力学的运动方程：

图1 结构计算简图Fig.1 Caculating diagram of structure

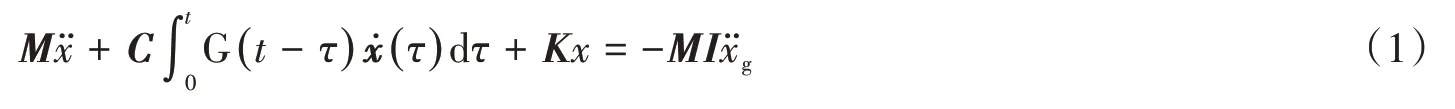
式中：、x分别为结构相对地面的加速度、速度、位移；K为结构刚度矩阵；C为阻尼系数矩阵；结构质量矩阵M= diag[m1m2…ml]g为地面运动加速度；G(t)为非粘滞阻尼系统的阻尼核函数。

指数型非粘滞阻尼系统的阻尼核函数可表示为：

式中：G(t)为非粘滞阻尼核函数；n为非粘滞阻尼松弛因子的总分支数；αi为松弛因子。

式中：Pij其中第j楼层处非粘滞阻尼器第i个分支阻尼力。

Kanai-Tajimi谱地震动模型可将地面运动表示为基于白噪声激励随机地震动：

地面激励为均值为零的Kanai-Tajimi地震动激励，将式（1）～式（5）扩阶，转换成新的一阶状态方程组：

式中：o1为l行零向量；o2为l行l列零矩阵；o3为l行nl列零矩阵；o4为nl列零向量；I1为l行l列单位矩阵；I2为nl行nl列单位矩阵；L为n列单位行向量；“T”为向量转置。

2 复模态解耦

根据复模态理论［13］，引入复模态变换：

式中：U为右特征向量矩阵；z为复模态变量。

将式（9）带入式（6），并左乘VT得：

式中：V为左特征向量矩阵；“T”为向量转置。

由式（10）可简化为：

由杜哈梅积分可得，式（11）的分量可表示为：

式中，zi、ηi分别为z、η的分量。

由式（7）、式（9）及式（12）则结构相对于地面的位移及速度可表示为：

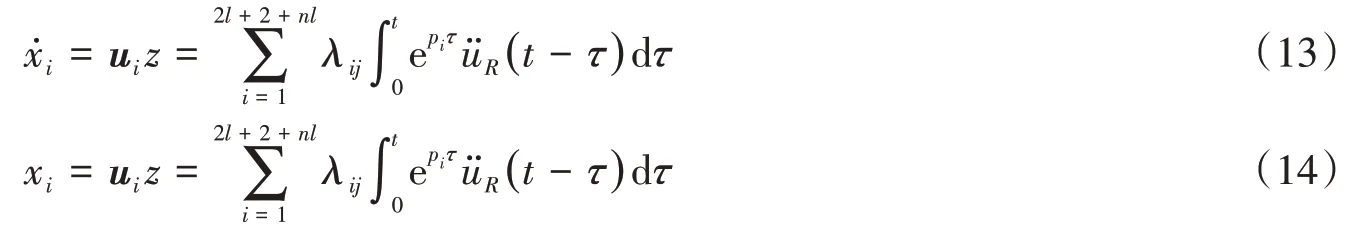
式中：ui为右特征向量矩阵U的第i行向量；结构响应的模态强度系数λij：

式中：uij为右特征向量矩阵U第i行第j列的元素。

3 结构响应的协方差、方差及功率谱分析

为简化行文，比较式（13）、式（14），结构的相对位移、相对速度可统一表达示为：

式中，结构的响应分量为：

式中，结构的相对位移及相对速度的模态强度系数μi=λij。由式（7）、式（8）可知，i= 1～l代表结构相对速度；i=l+ 1代表；i=l+ 2～2l+ 1代表结构相对位移x；i= 2l+ 2代表ug；i=( 2l+ 3 )～( 2l+ 2 +nl)代表非粘滞阻尼Pij；τ为时间差。

其结构响应的协方差可表示为：

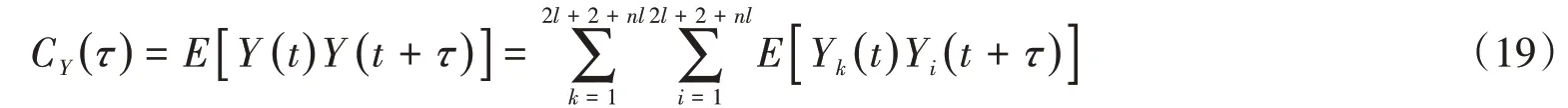
由式（19）可知，则结构响应分量的协方差为：

将式（22）带入式（21）得：

利用Dirac函数的性质，式（23）化为一重积分：

对式（24）积分得：

由式（19）、式（25），单自由度非粘滞结构基于Kanai-Tajimi随机激励下的响应为：

令：

式（26）可表示为：

当τ =0时，结构响应的协方差为结构响应的均方差：

由式（29）可知，结构响应的均方差可表示为结构振动特征值指数函数的线性组合。

根据Wiener-Khinchin关系，结构响应的单边功率谱SY(ω)为：

式中，ω为频域变量。

将式（28）代入式（30）得：

由式（27）、式（29）、式（31）得，文中所获得的结构基于Kanai-Tajimi 激励下的相对位移及速度的方差和功率谱的表达式为封闭解，且简洁明了。

4 结构响应的0～2阶谱矩分析

由随机振动理论［13］得Y(t)的i阶谱矩βY,i为：

把式（31）带入式（32），并令i= 0，则结构响应的0阶谱矩βY,0为：

对式（33）积分，则：

由文献［13］可知，平稳激励下的结构响应Yn的0阶谱矩βY,0，比较式（34）及式（29）两式完全相同，说明了文中方法计算0阶谱矩的正确性。由随机振动理论［13］可知，结构响应的速度的0阶谱矩等于其位移的2阶谱矩，即：

由谱矩的定义，1阶谱矩βY,1可表示为：

对式（36）进行积分得：

则1阶谱矩βY,1可表示为：

由式（34）、式（35）、式（39）可知，给出了结构相对于地面位移的0～2 阶谱矩简明封闭解，与文献［14，16－17］所提的方法相比，文中方法无需积分，故不受积分区间取值的影响。

5 算例

一栋4 层框架结构，结构第1～2 层质量m1～2= 5× 105kg，结构第3～4 层质量m3～4= 4.2 × 105kg；结构第1～2 层抗侧刚度k1～2= 2 × 109N/m，结构第3、4 层抗侧刚度k3～4= 1.8 × 109N/m；各层阻尼参数均为c= 2.5×106N ⋅s/m。非粘滞阻尼采用两分支指数型核函数［7－8］，G(t)=( α1e-α1t+ α2e-α2t)，α1= 25s-1，α1= 75s-1。随机地震动激励采为Kanai-Tajimi 谱，其相关参数［11］：特征频率为ωg= 15.71rad/s，场地阻尼比ξg= 0.72；白噪声强度因子S0= 31.76 × 10-4m2/s3。

5.1 地面加速度的功率谱对比分析

地面加速度可由式（4）、式（5）、式（7）、式（18）联立得：

式中，κi为地面加速度的模态强度系数且κi= -2ξgωgλ5,i-10,i，λ5,i、λ10,i含义见式（18）。

按文中方法，地面加速度模态强度系数κi如表1所示。

表1 地面加速度模态强度系数κi表Table 1 Modal intensity coefficients κi of ground acceleration

注：ξi = real(pi)/ ||pi 。

模态数1234567891 0 11 12 13特征值pi－11.311 2±10.902 3－0.504 4±23.432 5－1.904 1±65.139 6－2.605 6±103.357 9－2.935 2±125.235 0－24.159 8－24.225 1－24.273 7－24.622 4－69.894 7－70.615 5－71.937 7－74.371 6等效频率|pi|15.71 23.44 65.16 103.39 125.69 24.15 24.22 24.27 24.62 69.89 70.61 71.93 74.37等效阻尼比ξg 0.72 0.02 0.02 0.02 0.02 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00xg模态系数κi－11.311 2±0.416 5 000000000000

从表1 中可知，模态1 的特征值为复共轭项，其对应的等效频率与场地的ωg相等，等效阻尼比与场地的ξg相等的模态强度系数不为零，而其余模态强度系数均为0，这与场地的地震动仅与场地有关而与结构无关的特点所决定，从侧面说明文中方法的正确性。

5.2 功率谱对比

文中方法，基于Kanai-Tajimi谱的地面绝对加速度激励功率谱，由式（31）、式（40）得：

式中：该算例中，2l+ 2 +nl= 18，l为自由度数，n为每个自由度中不同作用阻尼数量。

传统方法中，基于Kanai-Tajimi谱的地面绝对加速度激励功率谱其表达式为：

图2 给出了文中方法与传统方法的加速度功率谱对比图，对比区间[ 0 50 ]，对比间距为2 rad/s，两者完全吻合，表明文中分析加速度功率谱的正确性。

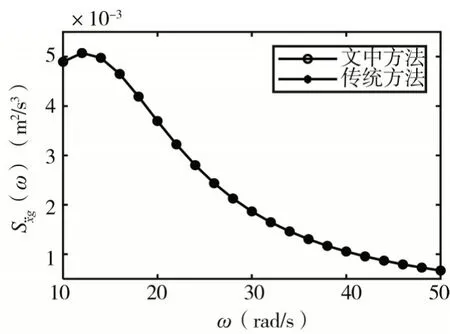
图2 加速度功率谱对比Fig.2 Comparison of acceleration power spectrum

文中方法，基于Kanai-Tajimi谱的多自由度结构的相对于地面的位移功率谱，由式（31）可得：

传统方法中，系统的幅频特性及其基于Kanai-Tajimi 谱的多自由度结构的相对于地面的位移功率谱其表达式为：

图3给出文中方法与传统方法中结构第1层位移响应的功率谱密度函数对比图，对比区间[ 10 50 ]，间距为2 rad/s，两者完全吻合，说明了文中方法分析结构响应功率谱密度函数的正确性。式（43）、式（44）相比，文中方法表达形式更为简洁。

图3 第1层结构位移功率谱对比Fig.3 Power spectrum comparison of structural displacement on the first floor

5.3 结构位移0～2阶谱矩精度及效率对比

在传统方法中，林家浩教授提出的虚拟激励法［14］在工程中应用较为广泛，文中与虚拟激励法进行对比：根据虚拟激励法［14］，将式（44）带入式（32）可得，结构位移0～2阶谱矩计算如下：

基于同一CPU，用Matlab进行精度、效率对比：上述响应值，采用数值方法在[ 0∞]区间进行求解是无法实现的，故虚拟激励法：频率积分区间取[ 0 300（]rad/s），其积分步长分别取3种不同工况（1、0.5、0.05 rad/s）所得结果的精度与本文所得结果精度进行对比，如图4～图6 所示：积分区间一定，0～2 阶响应谱矩精度与积分步长有关，其积分步长越小，结果越精确。从图像可得，积分步长为0.05 rad/s，其精度最好，文中方法与其完全重合，验证了文中方法所得结果精度较好。

图4 结构位移0阶谱矩对比Fig.4 Comparison of the 0-order spectral moments of structural displacement

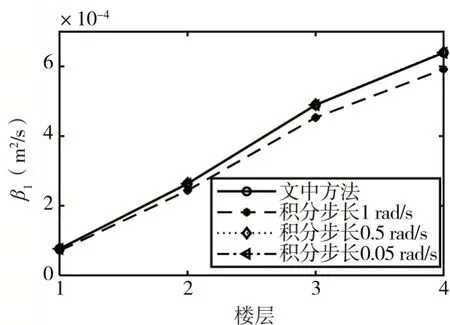
图5 结构位移1阶谱矩对比Fig.5 Comparison of the first-order spectral moments of structural displacement

图6 结构位移2阶谱矩对比Fig.6 Comparison of the second-order spectral moments of structural displacement

2种方法效率分析对比，由表2可得，文中方法计算结构的动力响应0～2阶谱矩的结果为封闭解，其不受积分区间的影响，其效率为积分步长1 rad/s 的1.2 倍；为积分步长0.5 rad/s 的1.9 倍；为积分步长0.05 rad/s的11.6倍，减小积分步长确实可提高精度，但效率也会随之降低，证明了文中方法效率较好。