机动车动荷载对地下综合管廊的影响分析
2022-07-21施有志阮建凑林树枝薛宏伟
施有志,阮建凑,林树枝,薛宏伟
(1.厦门理工学院土木工程与建筑学院,福建厦门 361024;2.厦门市交通运输局,福建厦门 361001;3.中交第三航务工程局有限公司厦门分公司,福建厦门 361003)
引言
城市地下综合管廊将各种市政管线容纳其中,能够解决反复开挖路面、架空线网密集、管线事故频发等问题,优化城市环境,确保道路交通功能充分发挥。位于主车道下的地下综合管廊,虽然有一定的覆土厚度,但在运营过程中不可避免仍要承受地面机动车的动荷载,特别是当地面平整度较差,车辆动荷载大等情况,管廊周边岩土不仅要承受地面车辆所带来的振动荷载,同时也将荷载传递至管廊结构,一定时间后,可能将导致主体结构发生损伤破坏[1]。
机动车动荷载对管廊的影响取决于很多因素,最重要的因素是车辆动荷载的大小,其次是管廊埋深、结构尺寸和覆土类型等。目前国内外学者对机动车荷载作用下管廊的响应特征研究较少,且主要从数值模拟方面开展,数值模拟的重要问题是对机动车荷载的确定。机动车荷载按其随时间的变化规律通常可分为静载模型、确定性动载模型、以及随机性动载模型3 类荷载模型[2]。静载模型将车辆的轮压简化为静荷载,常等效为均布恒载;确定性动载模型是将车辆荷载简化成随时间和位置按照某种规律变化的荷载,例如车辆荷载位置随时间变化的移动恒载和荷载大小随时间变化的波动荷载,除此之外还有在移动恒载的基础上考虑荷载简谐波动的移动简谐荷载;随机性动载模型由于其随机性不便于模拟,在设计与研究中不常采用。张斌等[3]利用谐波叠加法模拟了车辆随机荷载,详细分析了4 个车辆参数对于车辆随机荷载的影响。徐健等[4]采用半波正弦函数模拟单次车辆荷载作用,按一定加载周期将其施加于管廊典型剖面二维模型上表面,该方法属于二维非移动荷载,每一个时刻,荷载的位置未发生变化,只施加一次脉冲荷载。总之,车辆在路面行驶过程中具有较大的随机性,荷载作用也具有不均匀性,行车动荷载模型的假定影响计算结果。
关于行车动荷载对管廊的影响方面,黄运峰[5]和张缤等[6]通过MIDAS-GTS对车辆荷载作用下综合管廊变形沉降进行研究,分析了隔墙位置对双舱矩形综合管廊受力性能的影响。白旭峰等[7]采用ANSYS软件建立管廊土体相互作用模型,分析车辆荷载作用下软土地基上预制综合管廊的受力变形特征,发现车辆荷载的作用造成管廊出现明显的不均匀沉降现象,如果车道数增加这种不均匀沉降现象进一步扩大。李磊[8]采用ABAQUS 有限元软件研究管廊埋深对结构响应规律的影响,发现管廊底板对于埋深的敏感性较小,顶板大;通过分别考虑车速为40、60、80、100 km/h情况下的动力响应,发现不同车速下管廊顶板的Mises应力分布比较均匀,车速过大时会引起土体沉降增大。全勇[9]选取150、300、550 kN这3个车辆载重,并采用0.1、0.2、0.3和0.4这4个车辆动荷载系数来表征路面不平整度和车速的变化,发现车辆载重和车辆动载系数的增加会一定程度的加强车辆荷载对地下综合管廊的影响,但是随着车辆载重和车辆动载系数的增加,车辆荷载导致管廊管片的应力和竖向位移量以及地表沉降量增加的幅度较小。黄懿[10]借助现场实体试验及数值模拟,研究重载车辆作用下综合管廊的动力特性响应。张福麟[11]运用ABAQUS 有限元法分析了埋深对管廊竖向应力、内力和管顶附加位移,研究表明随埋深的增大,管廊结构内力由机动车荷载控制逐渐转变为土压力控制,在其转变的过程中竖向总应力最小的埋深,对管廊结构较为有利。
机动车动荷载可能对管廊结构产生疲劳损伤,影响其使用寿命,张福麟[11]通过混凝土受拉、受压疲劳寿命预测公式,分别计算整浇管廊与3种装配式综合管廊危险位置的疲劳寿命。
综上可知,国内外对机动车荷载对综合管廊的影响研究成果较少,且主要采用数值模拟分析,对影响因素的敏感分析也较少。基于此,文中以厦门市某主干道下的综合管廊工程为依托,采用现场试验方法,监测管廊的振动速度和频率;并建立有限元分析模型,揭示车辆荷载在土体中的衰减规律以及管廊的覆土埋深、断面舱数、地质条件和行车动荷载特点等影响因素对管廊动力响应情况的敏感度,并预测管廊结构的疲劳损伤特征。
1 机动车动荷载对管廊振动响应监测
1.1 振动监测试验
选择厦门市某主车道下的综合管廊作为试验段,该段管廊覆土约埋深1.5~3.5 m。管廊预制标准段采用弧形断面,净空为2.8 m×2.5 m,壁厚25 cm,采用钢筋混凝土结构,混凝土等级为C40防水混凝土,抗渗等级P8。管廊下设垫层,由15 cm厚C15素混凝土20 cm厚碎石组成。断面如图1所示。

图1 道路及管廊的横断面图Fig.1 Cross section of road and pipe gallery
现场使用水准仪定位高程并选择覆土1.62 m 的管廊断面作为监测剖面,如图2 所示。断面共布设2 个振动监测仪,分别布设在管廊结构侧墙中部、拱顶跨中处,如图3所示。

图2 振动监测剖面位置示意图Fig.2 Schematic diagram of vibration monitoring section location

图3 管廊结构测点布设示意图Fig.3 Layout of measuring points for pipe gallery structure
振动监测工作采用L20-S、BVA-S型测振仪以及TC-4850N无线网络测振仪,其包含拾振器及记录器。
1.2 监测结果分析
早高峰(7:00~11:00)期间质点峰值振动速度及主频率见表1,晚高峰(17:00~21:00)期间质点峰值振动速度及主频率见表2。

表1 早高峰各质点峰值振动速度及主频率对比表Table 1 Comparison of peak vibration velocity and main frequency rate of each particle in early peak

表2 晚高峰各质点峰值振动速度及主频率对比表Table 2 Comparison of peak vibration velocity and dominant frequency of each particle in evening peak
通过表1 和表2 可以看出,通道Z(竖向)在拱顶以及侧墙位置的振动速度均比通道X(纵向)、通道Y(横向)更大,早高峰期间振动峰值达0.041 cm/s,振动主频为11.3 Hz,晚高峰期间振动峰值达0.033 cm/s,振动主频为8.1 Hz。拱顶比侧墙在通道Y(横向)、通道Z(竖向)振动速度更大,而在通道X(纵向)拱顶振动速度则略小于侧墙测点。
2 机动车动荷载对管廊影响数值模拟
2.1 数值模型设计
根据机动车道下单舱管廊(图1)建立三维数值模型。模型沿管廊纵向尺寸(x轴方向)为40 m;沿管廊横向总尺寸(y轴方向)取为40 m,约为管廊跨度的10 倍;模型深度方向(z轴方向)自地表向下取12 m,模型底面距管廊基础约一倍管廊跨度。整个模型划分网格时,在管廊、路面附近适当加密网格,共划分37 893个实体单元,61 237个节点,如图4所示。地下水位埋深1.2 m。

图4 机动车道下单舱管廊三维网格模型Fig.4 Three dimensional mesh model of single cabin pipe gallery in motorway
三舱管廊的尺寸如图5所示,建立的三维几何模型如图6。

图5 三舱管廊三维几何模型Fig.5 Three dimensional geometric model of pipe gallery in Hatch No.3

图6 机动车道三舱管廊三维模型Fig.6 Three dimensional model of three cabin pipe corridor in motorway
土体、管廊结构和垫层均采用实体建模,采用10 节点高阶四面体单元划分土体网格。土体视为弹塑性材料,采用小应变土体硬化模型(HSS)模拟。根据地质情况分布,本节分析时考虑管廊周边土体均为粉质黏土地层。土性参数根据笔者之前的研究成果确定[12]。管廊结构假定为线弹性,采用线弹性模型(LE)模拟;管廊下方垫层采用莫尔-库仑模型(MC)模拟。材料参数见表3。沥青路面采用线弹性的板单元模拟,厚度d=0.05 m;重度γ=22 kN/m³;弹性模量E=300 kN/m²;泊松比ν=0.2。

表3 材料物理力学参数Table 3 Physical and mechanical parameters of materials
2.2 模拟方案
2.2.1 机动车道交通荷载三维模拟方法
移动恒载对应于车辆在路面上的一次通过,是将机动车荷载看成荷载大小不变,仅作用位置随时间变化的一种荷载模型,这种荷载模型忽略了车辆运动中产生的随时间变化的轮压波动,但相较于均布荷载更为贴近实际情况,因此目前在分析地下综合管廊纵向力学特性时较为常用,本次计算即采用这种方法,汽车静载取值参考《公路工程技术标准》(JTGB 01-2014)[13]。在PLAXIS 3D 中,移动载荷通过对荷载指定移动路径和移动函数来实现。该功能可应用于点荷载和线荷载的静态和动态部分。移动载荷具有2 个特征,即移动路径和移动函数,移动函数施加于作为移动路径的预定义的线上。通过三维模拟可以真正实现移动荷载的动态模拟及动态响应分析。
将移动荷载边界条件施加在三维模型上,荷载作用位置以一定的速度向前移动,可以真正实现车辆荷载的动态模拟,从而获得移动荷载作用下每一个时刻地下结构受到的来自真实空间位置荷载的动态三维响应。
2.2.2 分析方案
为分析车辆移动荷载作用下,车道下方单舱管廊的动力响应特征及可能产生疲劳破坏现象,设置2种分析方案,以考虑不同类型的车辆移动荷载。
(1)方案1:模拟城市交通常见的四轮小客车,车重1.6 t,单轮静载4 kN,以60 km/h(16.67 m/s)的速度行驶通过。
(2)方案2:模拟八轮大型货车,车重20 t,单轮静载25 kN,以60 km/h(16.67 m/s)的速度行驶通过。
为便于与现场监测数据进行对比,在模型中部设置与现场监测部位相对应的拱顶和侧墙位置监测点。
2.3 计算结果分析
2.3.1 管廊振动速度变化规律
方案1和方案2拱顶和侧墙各方向峰值振动速度实测值与计算值对比,如表4所示。

表4 特征点峰值振动速度实测值与计算值对比Table 4 Comparison of measured and calculated peak vibration velocity of characteristic points
由表4 可以看出,八轮20 t 重车引起的测点振动速度与实测结果更为相符,也就是说,实际交通负荷与方案2模拟的情况基本一致,同时也验证了数值模型的可靠性,为后续参数变化分析奠定了基础。
2.3.2 土体振动速度变化规律
图7、图8给出t=0.204 s,沿管廊中心纵剖面和沿监测点位置横剖面的土体竖向速度云图。

图7 方案1土体竖向速度云图Fig.7 Soil vertical velocity nephogram of Scheme 1

图8 方案2土体竖向速度云图Fig.8 Soil vertical velocity nephogram of soil of scheme 2
从图7、图8可以看出,随车辆荷载的移动,地表下方土体在轮压及车辆移动影响下的速度响应情况。方案1 车辆荷载相对较小,引起的下方土体振动速度较小,方案2 车辆荷载相对较大,在土体中引起的速度变化更为显著。总的来说,车辆移动荷载引起的土体振动速度在路面接触点附近最大,并随着深度的增加不断衰减;同时,管廊结构的存在对土体振动速度的传播起到了一定的阻隔作用。
2.3.3 管廊主应力变化规律
计算表明,方案1拱顶和侧墙的主应力在车辆通行过程中有小幅波动,拱顶大主应力σ1和侧墙小主应力σ3在-5.1~-8.4 kPa范围内变化。拱顶小主应力σ3和侧墙大主应力σ1分别在409~425 kPa和-319~-328 kPa范围内变化,变化幅度在4%以内。
方案2拱顶和侧墙的主应力在车辆通行过程中,拱顶大主应力σ1和侧墙小主应力σ3在-2.5~-11.4 kPa范围内变化。拱顶小主应力σ3和侧墙大主应力σ1分别在445~550 kPa和-326~-380 kPa范围内变化,变化幅度在20%以内。
3 机动车动荷载对综合管廊振动影响的参数敏感性分析
3.1 研究方案
为研究不同因素对行车动荷载作用下管廊结构响应特征的影响,考虑管廊结构跨度、埋深、舱数的变化,车速和同时通过的车辆数变化以及不同地层岩性,分析各参数变化引起的管廊结构振动响应特征的差异[14]。各分析方案参数变化情况见表5。其中砂层的参数见表3。

表5 模拟分析方案Table 5 Simulation analysis scheme
3.2 参数敏感性分析结果
3.2.1 单舱管廊跨度变化
单舱管廊跨度分别取3、4、5 m时,拱顶竖向振动速度随车辆通过时间变化曲线如图9所示。
总体上跨度4 m 和5 m 时的拱顶、底部竖向振动速度要明显高于跨度3 m 时的竖向振动速度。以拱顶为例,从图9 可以看出,跨度3 m 时的竖向振动速度峰值为0.007 cm/s,但跨度4 m 和5 m 时分别达到0.06 cm/s 和0.14 cm/s。此外,拱顶竖向振动速度要高于底部。以5 m 跨度为例,底部竖向峰值振动速度不超过0.02 cm/s,拱顶的竖向峰值振动速度达到底部峰值速度的7倍左右。

图9 单舱管廊跨度变化时管廊拱顶竖向速度随时间变化曲线Fig.9 Variation curve of vertical velocity of pipe gallery vault with time when the span of single cabin pipe gallery changes
3.2.2 单舱管廊埋深变化
单舱管廊埋深分别取1.5 m和3 m时,拱顶竖向振动速度随车辆通过时间变化曲线如图10所示。

图10 单舱管廊埋深变化时拱顶竖向速度随时间变化曲线Fig.10 Variation curve of vertical velocity of vault with time when the buried depth of single tank pipe gallery changes
总体上埋深1.5 m时的拱顶竖向振动速度峰值和波动幅度都要略高于埋深3 m的情况,但由于都属于浅埋,两者的差别不大。
随时间变化,拱顶和侧墙主应力的最大值如表6所示。
主应力值在车辆通行过程中的变化幅度很小。从表6可以看出,随着埋深增大,管廊结构的上覆土压力和围压都有所增加,拱顶和侧墙主应力也增大。

表6 不同埋深拱顶和侧墙主应力的最大值Table 6 The maximum principal stress of arch crown and side wall under different buried depths
3.2.3 管廊舱数变化
管廊舱数分别为单舱和三舱时,拱顶竖向振动速度随车辆通过时间变化曲线如图11所示。
从图11可以看出,总体上三舱管廊的拱顶竖向振动速度峰值和波动幅度在车辆通过测点断面过程中要明显高于单舱管廊的情况,三舱管廊的跨度要高于单舱,这一结果与前面跨度变化分析结果一致。
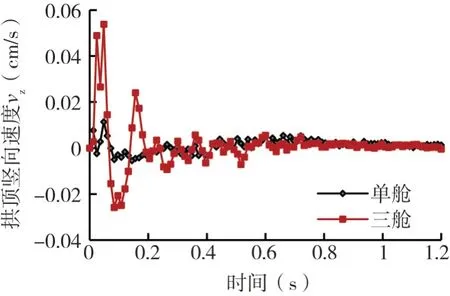
图11 管廊舱数不同时管廊拱顶竖向速度随时间变化曲线Fig.11 Variation curve of vertical velocity of pipe gallery vault with time when the number of pipe gallery tanks is different
管廊舱数变化时,引起的管廊拱顶和侧墙主应力变化形态基本不变,但拱顶小主应力(受拉)和侧墙大主应力(受压)的峰值则随管廊舱数变化而有显著变化。以拱顶小主应力σ3为例,三舱管廊拱顶测点σ3峰值为269 kPa,单舱时拱顶σ3峰值为425 kPa,变化幅度达58%。对于侧墙,单舱以受压为主,三舱则以受拉为主,可见管廊舱数变化及结构跨度及刚度变化对管廊结构主应力峰值有明显的影响。
3.2.4 地质条件变化
地层分别为粉质黏土层和砂土层时,拱顶竖向振动速度及主应力随车辆通过时间变化曲线如图12所示。

图12 地层土体性质不同时管廊拱顶竖向速度随时间变化曲线Fig.12 Variation curve of vertical velocity of pipe gallery vault with time when the properties of stratum soil are different
从图12可以看出,总体上地层土体性质变化引起的管廊拱顶竖向振动速度随时间的变化规律基本一致,速度峰值也较为接近,但地层为砂土层时,管廊拱顶竖向振动速度的波动幅度要略高于粉质黏土层时的情况。
地层性质变化时,引起的管廊拱顶和侧墙主应力变化形态基本不变,但拱顶小主应力(受拉)和侧墙大主应力(受压)的峰值则随地层土体性质变化而有显著变化,以拱顶小主应力σ3为例,地层为粉质黏土层时,σ3峰值为425 kPa,地层为砂土层时,σ3峰值为695 kPa,变化幅度达63.5%,可见地层土体性质对管廊结构主应力峰值影响很大,这与土体的强度、刚度等力学性质有关。
3.2.5 行车数量变化
当同时有1辆、2辆、3辆车通过时,拱顶竖向振动速度随车辆通过时间变化曲线如图13所示。
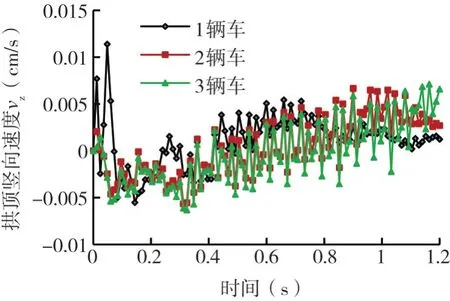
图13 通过车辆数不同时管廊拱顶竖向速度随时间变化曲线Fig.13 Variation curve of vertical velocity of pipe gallery vault with time when the number of vehicles passing through is different
通过图16可以看出,总体上通车数量不同时引起的管廊拱顶和侧墙竖向振动速度随时间的变化规律基本一致,但同时通过的车辆数越多,管廊拱顶和侧墙的竖向速度波动幅度相对越大。
同时通过的车辆数变化时,引起的管廊拱顶和侧墙主应力变化形态基本不变,但拱顶小主应力(受拉)和侧墙大主应力(受压)的峰值则随同时通过的车辆数增多而有微量增大。以拱顶小主应力σ3为例,通车1辆时,σ3峰值为425 kPa,通车2 辆时,σ3峰值为428 kPa,通车3 辆时σ3峰值为429 kPa,可见同时通过的车辆数对管廊拱顶和侧墙的主应力峰值影响很小。
3.2.6 行车速度变化
车辆行驶速度分别取40,60、80 km/h,拱顶竖向振动速度及主应力随车辆通过时间变化曲线如图14所示。

图14 不同车速时管廊拱顶竖向速度随时间变化曲线Fig.14 Variation curve of vertical velocity of pipe gallery vault with time at different vehicle speeds
由图14 可以看出,总体上车速变化引起的管廊拱顶和侧墙竖向振动速度的差异不大。此外,在车辆到达监测位置前,车速越高,引起的管廊拱顶和侧墙竖向振动速度越大,车辆通过监测位置时,车速越高,管廊拱顶和侧墙竖向振动速度反而越小。
车速变化时,引起的管廊拱顶和侧墙主应力峰值和变化形态不变,但主应力峰值出现的时刻则随车速变化,即车速越高,主应力峰值出现得越早,车速越低,主应力峰值出现得越晚,且波峰的宽度越大,如图15所示。

图15 不同车速时管廊拱顶主应力随时间变化曲线Fig.15 Variation curve of principal stress of pipe gallery vault with time at different vehicle speeds
3.3 机动车荷载下管廊疲劳寿命预测
Aas-Jakobsen对混凝土的单轴抗压疲劳损伤进行了研究[15-16],在早期研究中,以混凝土的最大最小应力为研究对象,得出了混凝土材料疲劳寿命与最大最小应力之间的线性关系表达式:

式中:N为疲劳寿命;R=为最大压应力为最小压应力;σc为混凝土材料的抗压强度标准值;β为调整系数,普遍取值0.068 5。
Cornelissen等总结得出了不同湿度条件下的混凝土疲劳寿命公式[17]:
潮湿条件下:
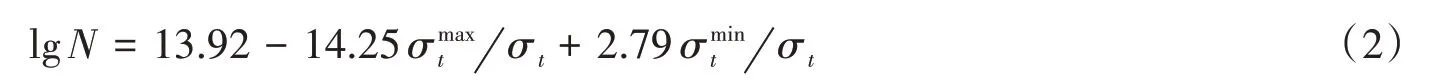
干燥条件下:

将管廊拱顶和侧墙关键点应力值汇总于表7。
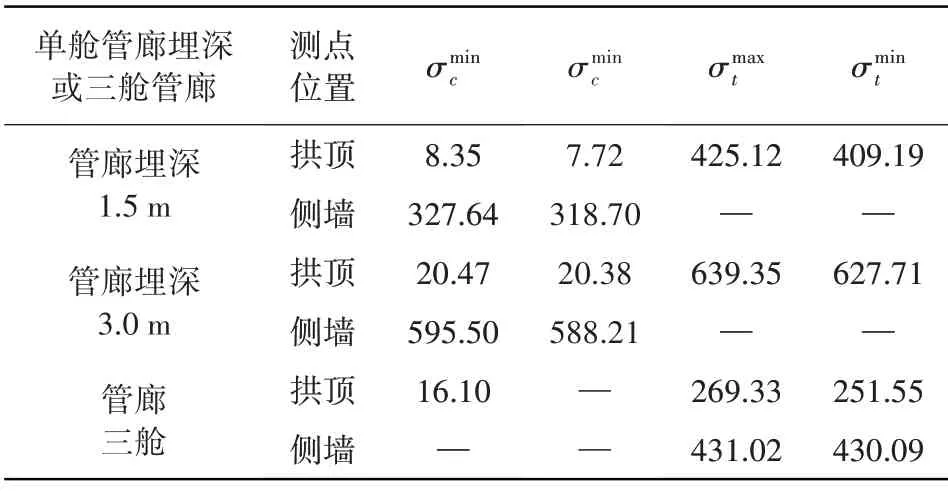
表7 管廊顶板及侧墙关键点应力Table 7 Stress at key points of pipe gallery roof and side wall kPa
混凝土的疲劳寿命预测方法,主要基于最大、最小的应力值及应力幅值对混凝土材料的极限疲劳次数进行预测。
对于疲劳公式的选取,对于危险位置压应力的验算,疲劳式(1)较为适合机动车荷载下的压应力波动疲劳计算。对于混凝土拉应力的验算,可选用式(3)。因此,将各关键点应力值分别代入式(1)和式(3),经计算得出各个关键点的极限疲劳次数统计见表8。其中,+∞代表由应力波动计算得出的极限疲劳次数无穷大,但实际情况下,由于混凝土材料会随时间发生劣化,无法达到次疲劳极限。

表8 管廊顶板及侧墙关键点极限疲劳次数Table 8 Limit fatigue times of key points of pipe gallery roof and side wall
由于管廊的疲劳寿命,除了受拉应力影响,还受其他因素(如管廊的温度、湿度等环境)的影响,因此,仅从受拉应力角度评价疲劳寿命并不妥当。但可以根据受拉应力较大的区域,在设计阶段采用适当措施改进设计,如增加钢筋混凝土结构抗力等措施,亦对提高管廊结构的疲劳寿命有一定的好处。
4 结论
文中以厦门某主车道下管廊为对象,通过现场实测结合数值模拟,研究机动车荷载对地下管廊的影响分析,并评价其疲劳寿命,得出以下结论:
(1)车辆自重对车道移动荷载作用下管廊的振动速度有一定影响。数值模拟中采用八轮重型汽车以60 km/h 速度通行时,峰值振动速度达到0.045 cm/s,与实测值0.041 cm/s相近,实际交通负荷可按20 t重型汽车荷载考虑。
(2)车辆移动荷载引起的土体振动速度在路面接触点附近最大,并随着深度的增加不断衰减;车辆移动荷载作用下,浅埋单舱管廊结构的振动速度与管廊结构的跨度密切相关,管廊跨度越大,其竖向振动速度峰值和波动幅度也越大。随着管廊埋深的增加,拱顶和侧墙主应力随埋深增加而增大。
(3)地层性质变化时,引起的管廊拱顶和侧墙主应力变化形态基本不变,但拱顶小主应力(受拉)和侧墙大主应力(受压)的峰值则随地层土体性质变化而有显著变化,变化幅度达63.5%,这与土体的强度、刚度等力学性质有关。
(4)车速变化引起的管廊拱顶和侧墙竖向振动速度的差异不大,管廊拱顶和侧墙主应力峰值和变化形态也基本不变。
(5)由于管廊的疲劳寿命,还受其他因素的影响,仅从受拉应力角度评价疲劳寿命并不妥当。但实际工程中可根据一定范围内的埋深不同,所受拉力的不同,设计将调整配筋,增加钢筋混凝土结构的抗力,而总体寿命取决于该抗力。
(6)根据计算结果,三舱管廊的应力更小,抗疲劳更有利。由于文中应用的公式未能准确反映交通荷载引起波动的影响,尚有待于对实际三舱管廊的实际振动情况的进一步验证。
