探讨强夯参数对路基加固效果的影响
2022-07-20张开兴
张开兴
(贵州佳源建设工程有限公司,贵州 贵阳 550001)
0 引言
强夯法是在重锤夯实法的基础上发展而来的一种新的地基处理方法,又称为动力固结法,工艺原理是利用起吊设备,将夯实锤提升至一定高度,由夯实锤自由下落夯基土层,使地基夯实固结[1-6]。该方法广泛应用于道路路基、房建地基等工程地基加固,可有效夯实碎石土、沙土、湿陷性黄土等地基。锤底半径、夯击能量是强夯工艺核心参数,对路基夯实加固效果具有重要影响[7-8]。该文以某高速公路路基加固工程为依托,探讨强夯参数对路基加固效果的影响,可为后期路基强夯施工参数设计提供依据。
1 工程概况
高速公路工程,全长1 671 991 m,起讫桩号LK2+840~LK20+711.991,双向四车道的设计,设计车速100 km/h,路基宽26 m,工程建设所在地土体以素填土、黏土、粉土、粉质黏土为主,力学性质较差,拟定采用强夯法加固路基。
2 数值建模
2.1 数值模型及材料参数
地质勘测报告揭露的场地土层分布自地表向下依次为:素填土、黏土、粉土、粉质黏土,平均层厚约为2 m、1 m、2 m、10 m[9],以地质报告揭露的土层分布、土层厚度为基准,建立土层分布数值模型,模型长长(X 轴)30 m,宽(Y 轴)30 m,高(Z 轴)15 m,原点坐标(0,0,0)位于模型底部中心,夯点位置坐标为(0,0,15),见表1(a);夯锤模型见图1(b),锤径取1.0 m,1.25 m,1.5 m。场地各土层土体力学指标见表1。
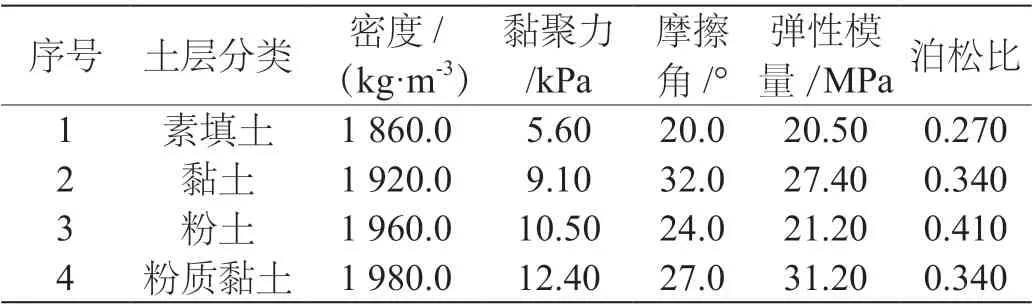
表1 土体的力学指标

图1 数值模型图
2.2 本构模型及网格划分
该文采用摩尔-库伦本构模型模拟土体性质。该模型网格数目为13 500 个,按照模型中各土层厚度分布,素填土层、黏土层、粉土层、粉质黏土层网格数分别为1 800、900、1 800、9 000 个;按照图2 所示接触力时程曲线,模拟锤重为10 t、15 t、20 t 时的夯击能量。
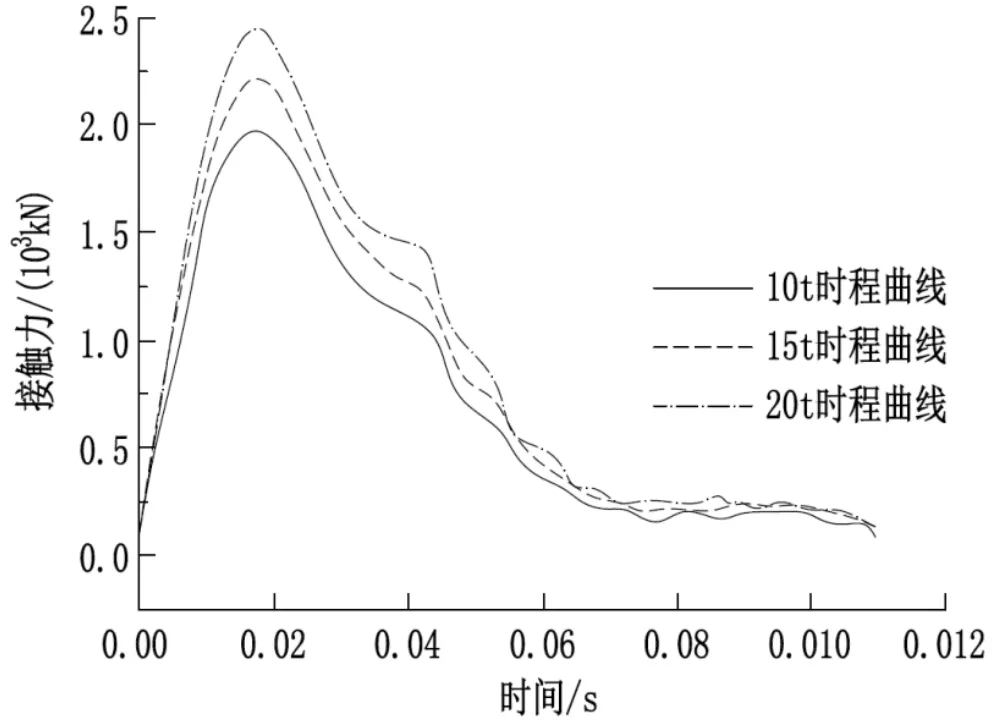
图2 接触力时程曲线
2.3 强夯工艺参数
锤径、锤重、下落高度是影响强夯工艺效果的核心参数,该文为降低研究难度、减少控制变量,采用夯击能量等效替换锤重、下落高度,由此,确定该次研究的强夯工艺参数为锤底半径、夯击能量;通过不同锤径、夯击能量下土体竖向位移、竖向应力、地表位移、夯坑体积变化特征,评价两项工艺参数对路基夯实效果的影响[10]。
3 数值结果分析
3.1 锤底半径影响
不同锤径下不同深度土体竖向变形数据见表2。

表2 不同锤径下土体竖向变形随深度变化数据统计表
由表2 可知:(1)同一锤底半径下,土体竖向变形量随土体深度增加而减小。
(2)0~3 m 范围内,同一土体深度下土体竖向变形随锤底半径增加而减小;相较于1.0 m 锤底半径,锤底半径为1.25 m、1.5 m 时,相同土体深度下土体竖向位移分别减少43.7%、62.5%。
(3)土体深度在4~6 m 范围时,锤底半径变化对土体竖向位移影响一致,表明土体深度在0~3 m 范围时对锤底半径变化敏感。
不同锤径下土体竖向应力峰值随深度变化曲线见图3。
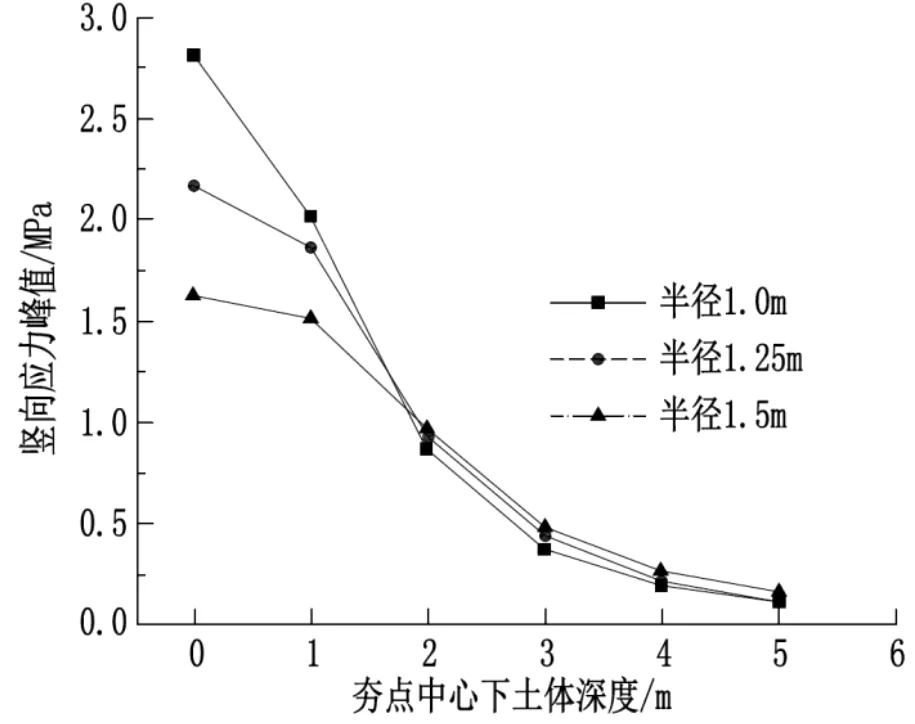
图3 不同锤径下土体竖向应力峰值随深度变化关系
由图3 可知:(1)三种不同锤底半径下,0~3 m 土层深度范围内,竖向应力峰值减小速度较大。
(2)土层深度在4~6 m 范围时,竖向应力峰值均在0.5 MPa 以内,减小速度较小。
(3)土层深度在0~3 m 范围时,竖向应力峰值变化对锤底半径变化较为敏感;相较于1.0 m 锤底半径,锤底半径为1.25 m、1.5 m 时,该土层深度范围内,竖向应力峰值分别减少18.5%、37.0%。
地表土竖向变形随锤径变化关系见图4。
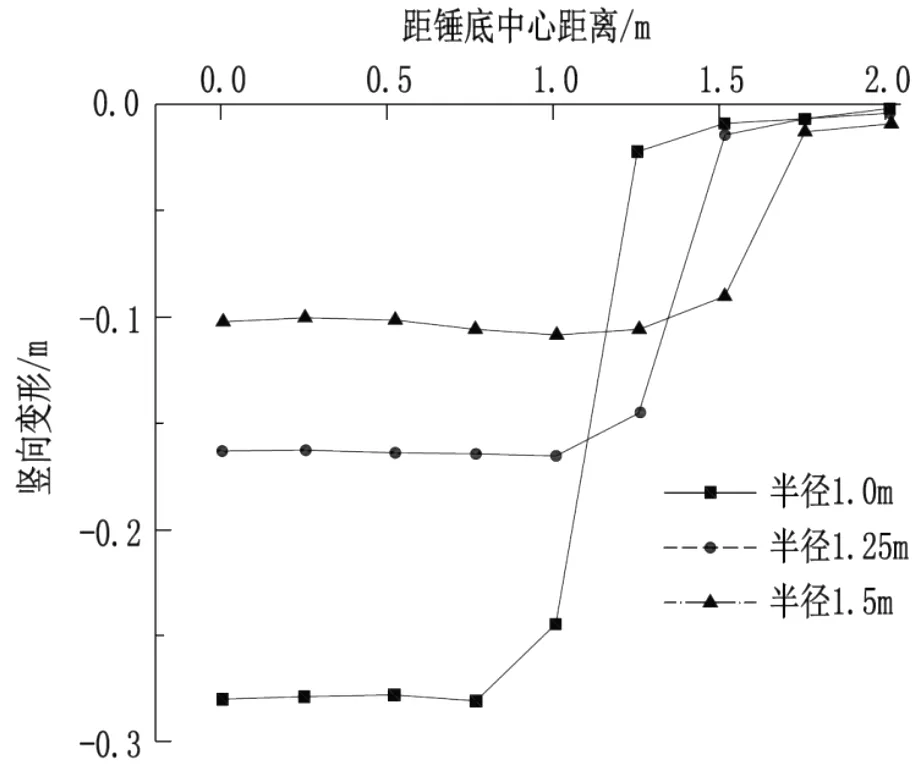
图4 不同锤径下地表土体竖向变形
由图4可知:锤底半径分别为1.0 m、1.25 m、1.5 m时,地表土体竖向变形影响宽度分别为1.3 m、1.5 m、1.8 m;锤底中心区域地表竖向位移值分别为0.28 m、0.17 m、0.10 m,可知随锤底半径增加,地表位移随之减小,夯击影响区域宽度随之增加,约为锤径的1.2~1.3 倍。
3.2 夯击能量影响
夯击能量为夯锤自重与夯锤下落高度的乘积,同一夯锤落距下,不同锤重对应的不同深度土层竖向位移量见表3。
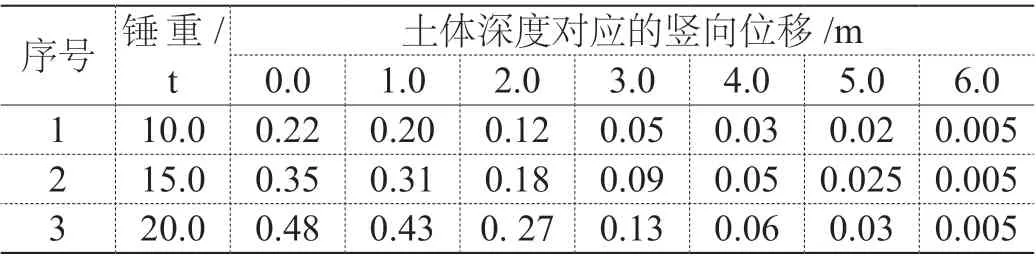
表3 相同落距不同锤重时土体竖向变形随深度变化数据统计表
由表3 可知:(1)同一锤重不同深度土层竖向位移深度随土层深度增加而减小。
(2)不同锤重同一深度土体竖向位移随锤重增加而增加。
(3)土层深度在0~3 m 范围内,土层竖向位移变化随锤重增加变化显著,4~6 m 范围内,土层竖向位移对锤重变化幅度较小,且最大影响深度均在6.0 m 左右。
同一落距不同锤重时土体竖向应力峰值随深度变化关系见图5。
由图5 可知:(1)不同锤重时,土体竖向应力随土层深度变化趋势基本一致。
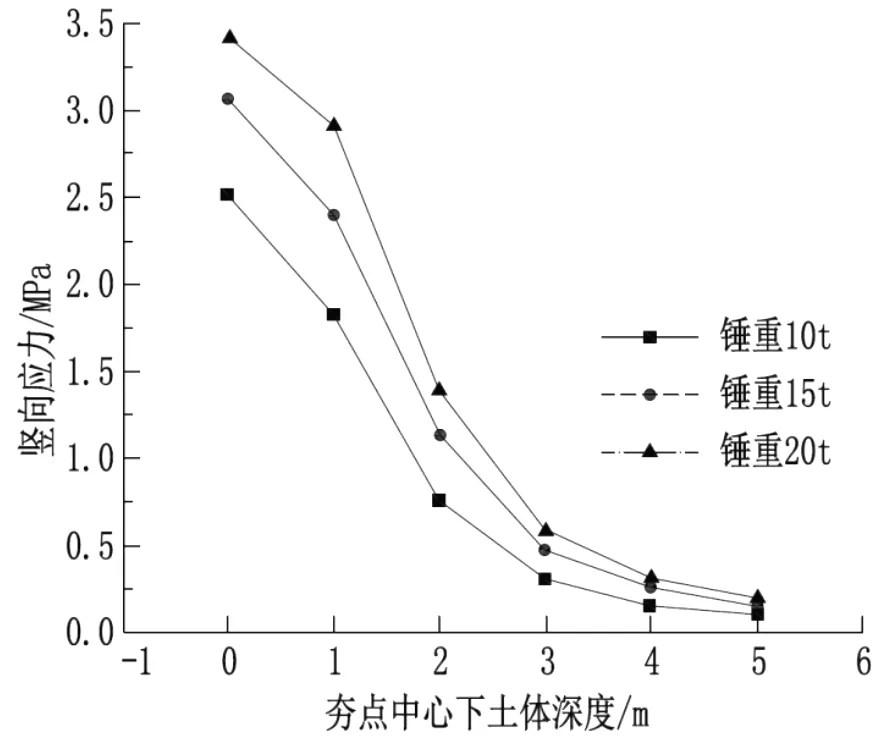
图5 相同落距时土体竖向应力峰值随深度变化关系
(2)土层深度在0~3 m 范围内时,竖向应力峰值减小速度较快。
(3)土层深度在4~6 m 范围内时,竖向应力峰值均小于0.6 MPa,峰值变化较小。
(4)综上可知,土体竖向应力随锤重增加而增加,土层深度在3 m 以内时,锤重对竖向应力值影响较大。
地表竖向变形随锤重变化曲线见图6。

图6 不同锤重时地表土体竖向变形
由图6 可知:(1)随锤底半径增加,地表竖向变形影响宽度随之增加。
(2)随锤重增加,地表竖向变形影响宽度不变,表明地表竖向变形影响宽度不受锤重(夯击能量)影响。
(3)锤重分别为10 t、15 t、20 t 时,地表竖向位移最大值分别为0.21 m、0.32 m、0.47 m,表明地表竖向位移随锤重增加而增大。
夯坑体积随锤重变化关系见图7。
由图7 可知:锤重分别为10 t、15 t、20 t 时,夯坑体积分别为473.3 m2、746.7 m2、1 080 m2,夯坑体积随锤重增加呈线性增大趋势。
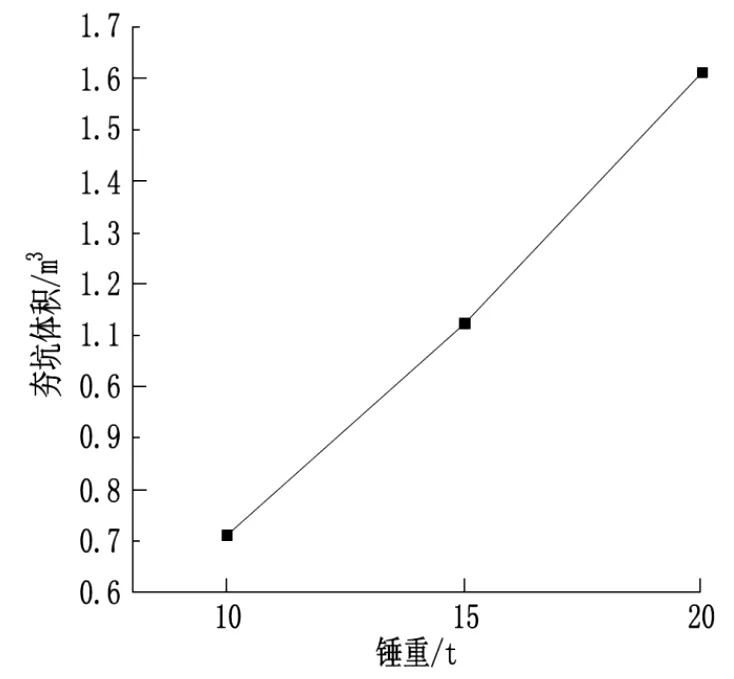
图7 夯坑体积随锤重变化关系图
4 结论
该文依托具体工程,通过数值分析软件,研究了锤底半径、夯击能量两项强夯参数对土体竖向位移、竖向应力、地表位移及夯坑体积影响,结论如下:
(1)土体深度在0~3 m 范围内,地表位移、地表峰值应力随锤底半径增加而减小,相较于锤底半径为1 m下的地表位移、地表峰值应力,锤底半径为1.25 m、1.5 m 时地表位移分别减小43.7%、62.5%,地表峰值应力分别减小18.5%、37.0%。
(2)随锤底半径增加,地表最大位移随之减小,地表夯击影响宽度随之线性增加,约为锤径的1.2~1.3 倍;随锤重增加,土体竖向峰值应力、土层位移随之增加,夯坑体积呈线性增加趋势。
(3)不同锤重夯击影响深度基本在6 m 左右。
