MIMO信道盲均衡算法的设计与实现

李素平

（巢湖学院电子工程学院，安徽巢湖 238000）

为了适应现代社会的通信需求，移动通信技术无论是信道速率、通信容量还是信息的可靠性方面都需要进一步提升，这也是拥有高频谱利用率并且能够有效对抗衰落特性的MIMO 技术被广泛关注的主要原因[1-2]. MIMO 技术可以充分地利用信道的空间资源，但是多输入多输出的信道也是产生码间串扰的重要因素. 高速无线通信系统中码间串扰的影响尤为显著，码间串扰的出现会破坏通信质量，导致通信过程出现杂音，甚至无法正确传输信号[3-4].考虑到均衡技术能够对信道进行补偿，对码间串扰进行有效抑制，因此均衡技术常用于MIMO 信道中，以改善系统性能. 传统均衡技术需要对发送数字序列进行训练学习，训练序列是牺牲了信道的带宽资源换取的[5-7]. 盲均衡技术不需要预先发送训练序列，仅根据信道中发送序列的一些先验信息就可以恢复输入信号，极大地节省了信道资源也提高了信道频谱利用率[8]. MIMO 系统与盲均衡技术配合使用，既可以一定程度上消除码间串扰，也可以保障系统较高的频谱利用率. MIMO 信道盲均衡技术具有极大的应用价值，是下一代移动通信技术探索的方向之一.

1 MIMO 通信系统

MIMO 技术与传统的单输入单输出（SISO）技术相比具有更大的信道容量和更高的数据可靠性，但是需要更多的天线[9]. MIMO 系统的接收端和发送端都使用多根天线，其在不改变带宽和天线发射功率的同时达到了改善信道衰减、提高系统容量、降低信道相关性的效果[10-11]. 对于MIMO 通信系统而言，码间串扰是一个无法避免的问题. 盲均衡技术能够对传输系统中的信道进行均衡，产生与信道特性匹配的补偿器，很好地解决码间串扰问题[12].

2 盲均衡算法原理

无线通信系统中的均衡技术主要分为两类：有训练序列的均衡和无训练序列的盲均衡. 在发送端不加入训练序列，利用接收信号的统计特性直接对均衡器的抽头系数进行估计的方法称为盲均衡.1975 年日本学者Sato 首先提出了盲均衡的概念，自此之后，许多科学家开始涉足盲均衡技术领域. 如今，盲均衡技术的研究主要在下述四个方面：基于神经网络的盲均衡、基于高阶谱的盲均衡、基于信号检测的盲均衡和Bussgang 类盲均衡等[13]. 对于MIMO信道均衡国内外学者们提出了多种解决方案. Lupupa 提出了分数阶系统辨识与均衡方法[14]，Mallick设计了基于恒模算法的光接收机盲均衡系统[15]，考虑到MIMO-OFDM 系统，文献[16]给出了回归加权恒模算法进行信道均衡，Pavan 提出了一种适用于MIMO 通信系统的数字鲁棒盲均衡方案[17]. 国内学者王旭光等提出了基于余弦代价函数的盲均衡算法[18]，肖可馨等给出了非常数模半盲均衡方案[12]，文献[19]基于改进差分进化算法对信道均衡进行了研究.

传统的线性自适应均衡技术计算量简单，但会占用较大频谱资源，传输系统有效性偏低. 而盲均衡技术无需训练序列，可有效解决前者占用较大带宽的问题，但同时会增加计算量.Bussgang 类盲均衡算法的目标是对均衡器输出端的信号进行非线性变换，通过设定代价函数，运用自适应算法调整均衡器权系数.下面主要分析Bussgang类盲均衡中的CMA算法和NCMA算法.

2.1 CMA算法原理

1980 年Gordard 首次提出了恒模盲均衡算法，该算法对所有恒模信号都适用，如适用于移相键控等信号，其代价函数为：

式中：p为正整数，| | 表示信号模值，Rp的表达式为：

当p=2时，就是CMA算法，其表达式如下：

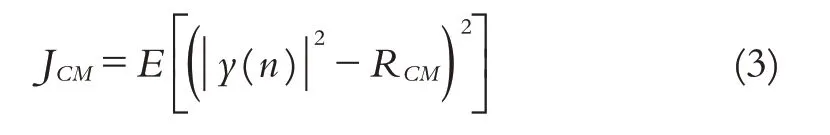
其中RCM是发射信号中与高阶统计量有关的一个常数.

CMA 算法代价函数的物理意义在于最小化输出信号的模值平方与常数RCM的距离. 当使用随机梯度下降法对代价函数进行优化时，就可以使输出信号的模值平方逐渐逼近常数RCM. 如果对CMA 的代价函数进行偏导计算，并用瞬时值来取代均值，则有：

由随机梯度下降法，可得：

2.2 NCMA算法原理

CMA 算法的运算并不复杂，但是由于参数受限，收敛性能会受到影响. 结合了归一化方法的NCMA 算法通过改变最小判决准则，使均衡器的输出达到信道的期望值，相比于CMA算法具有更快的收敛速度，收敛性能得到了提升. 抽头方程式更改为公式（7）：

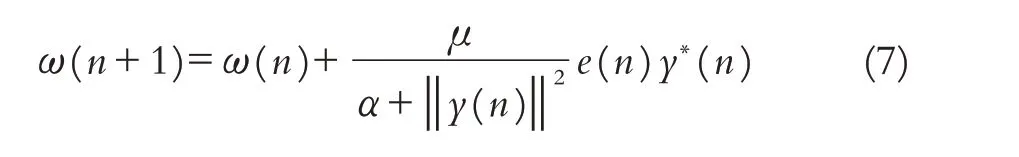
归一化恒模算法的迭代公式为公式（8）和公式（9）：

第j个均衡器的输出为：

3 MIMO-NCMA算法仿真及分析

利用MATLAB 对MIMO-NCMA 算法进行仿真，并分析该算法的收敛性、星座图等性能参数. 仿真实验中，信道输入端采用QPSK 调制信号，发送信源信号总数为12 000 个，噪声环境为30 dB 高斯白噪声且与输入信号是不相关的，步长μ=0.01，均衡器抽头个数为12个.

在上述仿真环境下，根据公式（7）对均衡器抽头系数进行迭代，当迭代次数为100 时，仿真结果如图1 所示. 可见均衡器输出信号星座图的位置不清晰且误差收敛曲线波动较大.

当迭代次数为1 000 时，仿真结果如图2 所示.可见均衡后信号的星座图较为清晰，提高了接收信号的判决准确率，降低了系统误码率.

图2(d)表明，对于NCMA 算法而言，迭代次数达到200 次以后收敛曲线就趋于稳定，由此可见NCMA算法的收敛速度是比较快的.

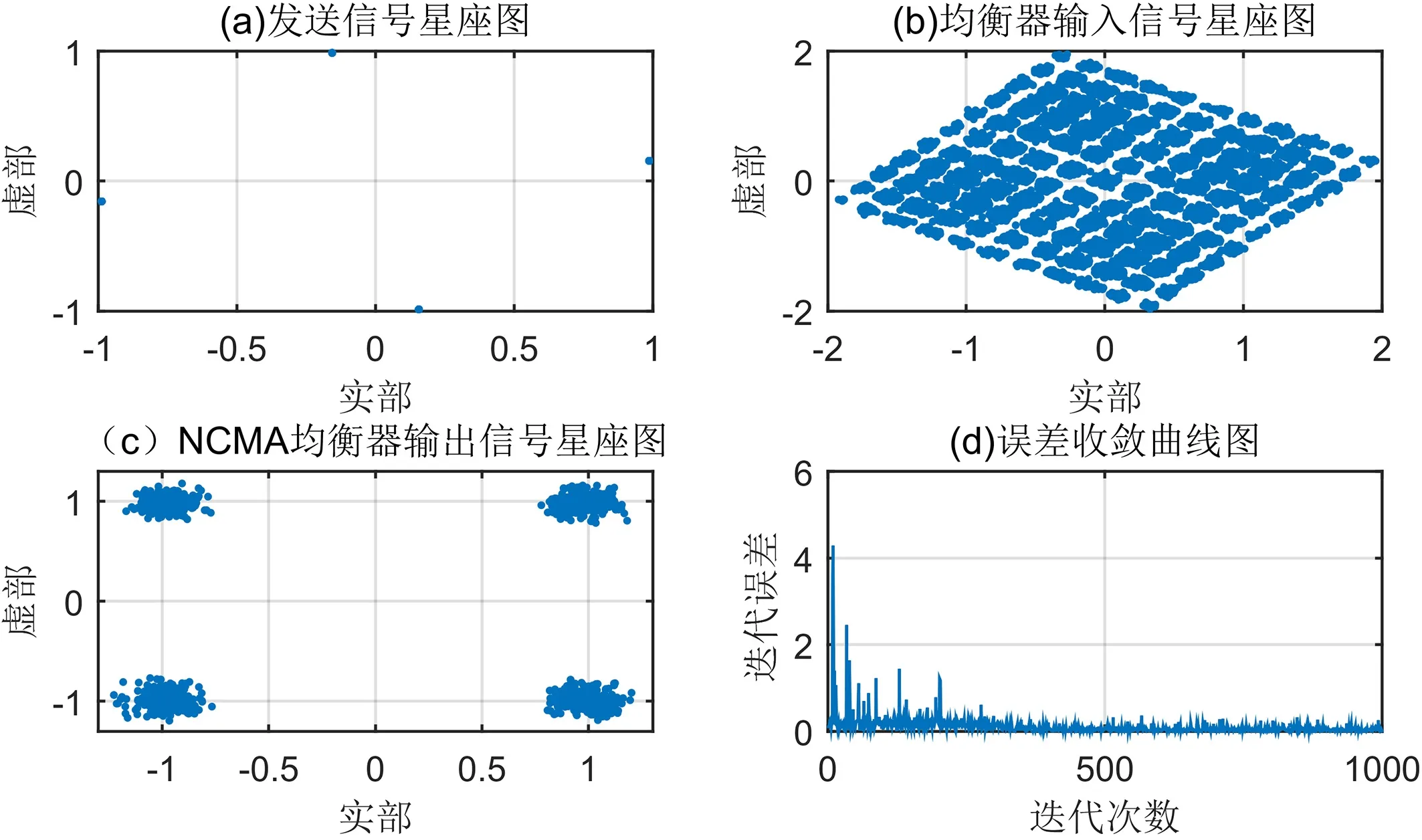
图2 NCMA算法迭代次数1000时的仿真图

当迭代次数为10 000时，仿真结果如图3所示.

图3 NCMA算法迭代次数10000时的仿真图

对比分析不同迭代次数时的仿真结果发现，当迭代次数为100 时，由图1(c)的均衡后接收信号星座图大致可以判断出原始星座图位置，但是其中有很多噪声小点，并没有达到预期的均衡效果.由图2和图3 可以看出，随着迭代次数的增多，均衡后信号星座图呈现得更加密集、紧凑，也便于观察者更为清晰地判决原始信号所在位置，从而有效地降低接收信号的误码率，提高系统可靠性. 由不同迭代次数仿真误差收敛曲线可以看出，当迭代次数减少时，几乎无法达到稳定的收敛状态，随着迭代次数的增加则收敛性能越来越稳定. 因此，NCMA 算法是存在局限性的，需要的迭代次数偏大，对运算时间有要求.

4 MIMO-CMA 算法仿真及分析

CMA 算法仿真环境与NCMA 算法的仿真环境相同，均衡器抽头系数的迭代参见公式（6）. 当迭代次数足够多时，CMA 和NCMA 两种盲均衡算法对MIMO 信道中的QPSK 信号都取得了相对理想的均衡效果. 对比图3 和图4 中的误差收敛曲线可以看出，CMA 算法达到稳定状态前其误差波动较大，且稳定时需求的迭代次数也相对较多. 由此可见，NCMA 算法的收敛速度快于CMA 算法，且稳定性能更佳，这也是NCMA 算法广泛地应用于实际均衡系统中的原因之一. 但是，恒模算法的代价函数是与幅值相关联的，与相位无关，对于信道中原始信号存在的相位偏移不敏感，不能很好地还原出相位偏移信号中的相位信息.

图4 CMA算法迭代次数10000时的仿真图

5 结语

本文研究了CMA 算法和NCMA 算法，对MIMO-NCMA 通信系统和MIMO-CMA 通信系统都进行了仿真. 均衡器输入信号星座图与信均衡器输出号星座图相比较，可以看出CMA 算法和NCMA算法都具有较好的均衡效果. 改变迭代次数可以得到不同的均衡效果，迭代次数越多，均衡后输出信号的星座图就越紧密，均衡效果越好. 在收敛速度上NCMA 算法比CMA 算法效率更高，但NCMA 算法存在运算量较大，对运算时间有要求且对信号相位不敏感的问题. 后续研究中，需要更多地关注NCMA 算法的迭代运算，降低计算量，使MIMO-NCMA 系统更加完善.同时，对于相位比较敏感的信号如图像信号，需要进一步修正恒模算法，以提取信号中的相位信息，提升信号识别率.