一类2n+1次多项式系统的焦点量及极限环的唯一性

谢向东，薛亚龙，许丽莉

（宁德师范学院 数理学院，福建 宁德 352100）

微分多项式系统的焦点量计算及极限环的个数判定一直是微分方程定性理论的热点问题之一，它因希尔伯特第十六问题而备受世人瞩目.近年来，高次多项式系统的研究日益受到广大学者的关注，研究成果层出不穷.

将文献[1]所研究的多项式系统推广为如下的2n+1 次多项式系统，并且得到了与文献[1]相似的结论，这里n是大于1的整数.

首先讨论系统(1)奇点的分布情况.

当b≥0时，O(0,0)是系统(1)唯一的奇点，是焦点或结点.

由于b＜0 时，y=是系统(1)的积分直线，系统(1)围绕O(0,0)如果存在极限环，则其只能介于两直线y=之间.

由上面的分析知，可做时间变换(1+by2n)t=t1，为了方便书写，仍记t1=t，则系统(1)变为等价形式

或消去x得到

它等价于Liénard 系统

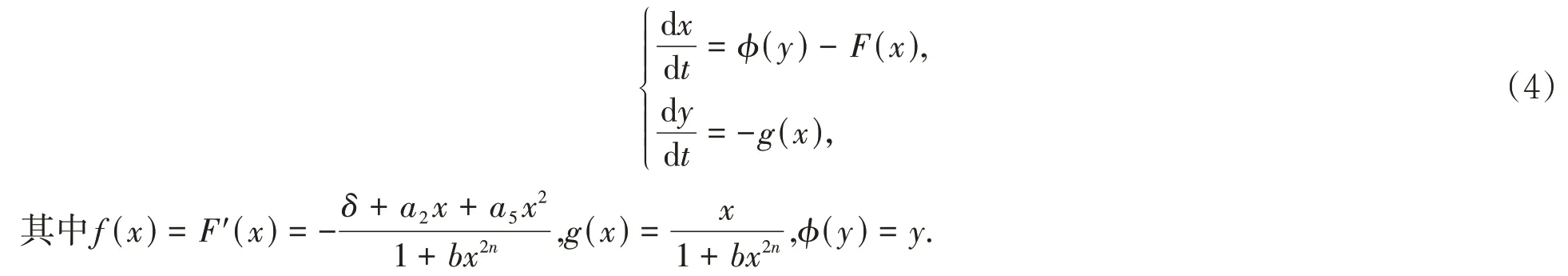
以下考虑系统(4)在O(0,0)的焦点量，而焦点量的符号决定了系统在奇点的稳定性，从而可能决定极限环的个数，这种方法可参见文献[6-7].

定理1对于系统(4)（或（1）），奇点O(0,0)的0 阶焦点量W0=δ，当δ=0 时1 阶焦点量是W1=a5，其中W0＞0或（W0=0,W1＞0），对应的O(0,0)是不稳定的，W0＜0或（W0=0,W1＜0），对应的O(0,0)是稳定的，如果W0=W1=0，则奇点O(0,0)为系统(1)的中心.

证明设W(x,y)=x2+2y2+(δy-x)2，则

显然，当r充分小时，|Δ2|≪|Δ1|，所以奇点O(0,0)的稳定性由δ决定，当δ＞0时，奇点O(0,0)是不稳定的；当δ＜0 时，奇点O(0,0)是稳定的，所以W0=δ，并且W0＞0(＜0) 时，O(0,0)是不稳定（稳定）焦点或结点.为了判断细焦点O(0,0)的稳定性，令W0=δ=0，将系统(1)化为系统(4)，并将f(x),g(x)在x=0附近展开成幂级数

由文献[4]的结论（见文献[1]的引理1），并沿用文献[4]的记号，有g3=β1=-，由于文献[4]中g3＞0(＜0)对应1 阶稳定细焦点（1 阶不稳定细焦点），与通常奇点稳定性的方向相反，故取W1与g3反号，再略去非0的正系数，可得当δ=0时，W1=a5.

以下证明当W0=0,W1=0时，O(0,0)为系统(1)的中心.记

当W0=0,W1=0，即δ=a5=0，此 时P(x,y)=-y+a2xy,Q(x,y)=x(1+by2n)，所 以P(x,-y)=-P(x,y),Q(x,-y)=Q(x,y).

所以系统(1)的积分曲线关于x轴是对称的，易知此时O(0,0)外围充满了闭轨线，故O(0,0)为系统(1)的中心，证毕.

定理2当W0W1≥0时，系统(1)围绕O(0,0)无极限环.

证明首先证明系统(1)关于参数a5和δ都构成广义旋转向量场.设δ1＞δ2，则

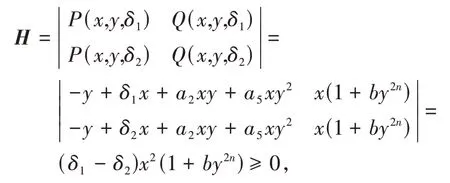
且等号仅当x=0时成立，故系统(1)关于δ构成广义旋转向量场.

且等号仅当x=0或y=0时成立，故系统(1)关于a5构成广义旋转向量场.

以下可以分三种情形1）W0=0；2）W1=0；3）W0W1＞0分别证明系统在O(0,0)外围不存在极限环，与文献[1]定理2的证明类似.

定理3当W0W1＜0 时，系统(1)围绕O(0,0)至多有一个极限环，且在小参数范围内必定存在一个极限环.

证明通过扰动1 阶细焦点，且改变焦点稳定性，系统(1)在O(0,0)的小范围内必定存在极限环.此外W0W1＜0 等价于a5δ＜0.作变量替换(x,y,t) →(-x,y,-t)，可以将参数a5,δ,a2同时改变符号，所以以下不妨设a5＜0,δ＞0.考虑系统(1)的等价形式

由于a5＜0,δ＞0，因此，由文献[5]的定理4.7知系统(1)(或(4))至多有一个极限环.