建筑地基深基坑开挖底面变形风险控制研究

李 帅 杜立杰 张 杰 樊翠银

（ 北京速测信息科技有限公司，北京 100080）

0.引言

随着建筑施工技术的不断成熟，对建筑地基深基坑开挖底面变形的控制精密度要求也越来越高。 采用有限元技术， 建立建筑地基深基坑开挖底面变形风险控制模型，通过有限元特征分析和承载应力分析的方法，在裂缝模式和拉压薄膜效应模式下进行建筑地基深基坑开挖底面变形特征分析，采用薄膜效应阶段荷载-位移曲线分析，建立建筑地基深基坑开挖底面变形风险控制曲线分布模型，通过极限应力特征分析， 实现构件的整体结构分析和风险控制。

目前， 国内外学者对建筑地基深基坑开挖底面变形风险控制的研究较多， 包括基于双向板承载力计算的变形风险控制方法、 基于微分方程和艾里应力函数水平约束的风险控制方法、基于三阶段荷载-变形模式的变形风险控制方法等[2,3]。 文献[4]中提出基于钢筋应变差的混凝土双向板极限状态分析及地面变形风险控制方法， 结合板壳有限元理论，编程计算建筑地基深基坑开挖底面变形特征，但该方法没有考虑受拉薄膜效应的影响， 变形风险控制的适应度不高。 文献[5]中提出型钢混凝土异形柱基于损伤的恢复力模型及变形控制方法，考虑二阶矩效应、轴压附加抗侧刚度、强度衰减，通过参数控制，实现建筑地基深基坑开挖底面变形风险控制，但该方法对变形控制的拟合度不高。针对上述问题，本文提出基于弹性段-强化段为双折线拟合控制的变形风险控制方法。 首先建立建筑地基深基坑开挖底面变形的试件参数分析模型， 通过对不同工况的底面变形风险差异度分析， 然后进行钢筋和混凝土间粘结滑移作用分配和承载力计算，最后进行实验测试，展示了用本文方法进行建筑地基深基坑开挖底面变形风险优化控制能力方面的应用性能。

1.试件结构模型

建立建筑地基深基坑开挖底面变形的试件参数分析模型， 在进行建筑地基深基坑开挖底面的变形特征分析中，基地在无穷远处受静水压力的作用，忽略重度梯度的影响。 结合构件滞回特性分析，通过松弛等力学行为参数分析，进行建筑地基深基坑开挖底面的应力评估和屈服响应分析。基于Maxwell体和Kelvin模型，进行时效变形行为特征分析， 采用Burgers蠕变模型进行Abel黏性元件的本构特征分析，实现对建筑地基深基坑开挖底面变形的结构参数模拟。 采用串联法则，进行微分-积分卷积计算，以Maxwell体和Kelvin模型为基础，通过虎克弹性体本构特征分析，得到建筑地基深基坑开挖底面变形的Burgers蠕变模型（ 如图1所示）：

图1 建筑地基深基坑开挖底面变形的Burgers 蠕变模型

由图1可知：ηK为虎克弹性体的本构系数；EM为黏滞系数；ξM为应力参数；α为受静水压力作用下的变形系数。 在基于围岩与衬砌的相互作用下， 采用围岩与衬砌的相互控制，进行变形风险抑制，得到建筑地基深基坑开挖底面变形结构参数（ 如表1所示）：

表1 建筑地基深基坑开挖底面变形结构参数

根据表1试件设计模型参数， 采用网格结构模型构建衬砌栅和支护结构栅，进行变形风险控制（ 如图2所示）：

图2 变形风险控制的栅格结构

2.开挖底面变形沉降模态分析

摇摇结合构件滞回特性分析， 采用最大累计沉降控制方法分析建筑地基深基坑开挖的沉降模态，给出建筑地基深基坑开挖底面变形沉降风险控制的约束参数和变量含义描述如下：X为对屈服后(受拉薄膜效应)阶段混凝土中心的位移；θ为混凝土压碎破坏的模型参数；δ，δ2分别为建筑地基深基坑开挖底面变形下塑性铰线的损伤系数和抗拉强度；MP,MR分别为y方向两钢筋应变测点；JR=JRL=JRR,JPθ,JPδ分别为双向板薄膜效应机理参数及钢筋应变， 表示约束转动惯量参数；R为混凝土简支板承载参数；L为最大裂缝宽度；D为试验板荷载-挠度距离; Km,Ke为裂缝开展和钢筋屈服；UL,UR为最大裂缝宽度及传导系数。 以上各变量均采用国际单位。 采用有限元分析方法进行建筑地基深基坑开挖底面变形的应力屈服响应分析。

假设建筑地基深基坑开挖的单元应力向量为n， 应变向量为ξ，则基底跨中出现大量网状裂缝表达如式（ 1）所示：

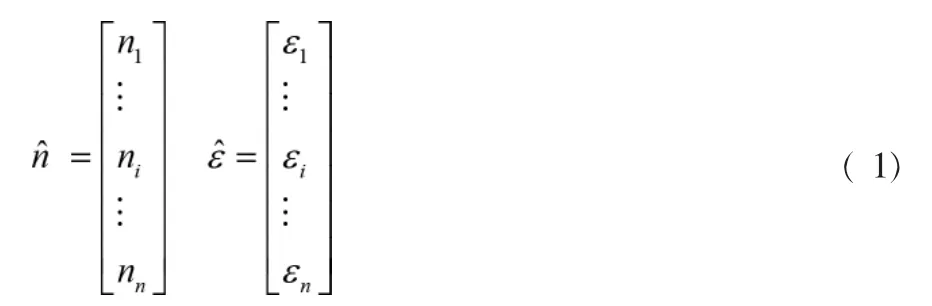
式（ 1）中，ni，εi分别为各个测量点的裂缝开展度和钢筋屈服。 在最大应力状态下，最大裂缝宽度约为0.2mm，引入抗弯刚度软化系数， 得到荷载-平面内位移分布的弹性模量关系Gn表示为：

其中，

式（ 4）中，E为获得后期压力数据的弹性模量；Si为第i组变形位置节点的板角约束力；Ai为单位跨中竖向挠度。

根据上述分析，建立了建筑地基深基坑开挖底面变形的试件参数分析模型， 通过位移边界条件层面分析的方法，采用ANSYS有限元软件建立有限元模型。

3.开挖底面变形风险控制模型优化

通过ANSYS 有限元软件模拟基深基坑开挖底面的弹性段-强化段双折线分布问题， 通过对不同工况的底面变形风险差异度分析， 计算后期各板角约束力的水平位移之和，如式（ 5）所示：

式（ 5）中，dei为支护结构相互作用矩；UR为偏应力；n为高压缩性元件的个数；t0为岩体的不可压缩特征参数。进而得到底面弹性变形的高压缩性元件满足Ds，如式（ 6）所示：

式（ 6）中，Dr为支护压力的积分截面数；δ为高压缩性元件的个数；l为试件长度；E1为径向和切向偏应力；σ为压缩应力系数。构造混凝土衬砌的扭矩-扭转角滞回曲线，分布曲线关系，如式（ 7）所示：

式（ 7） 中，Vt1为截面距掌子面的距离；Vu1为剪切模量；ΔVt为无限大平面孔洞映射差。 通过对不同工况的底面变形风险差异度分析，进行钢筋和混凝土间粘结滑移作用分配和承载力计算，如式（ 8）所示：

式（ 8）中，a1=1/2，a2=25，a3=8，a4=20，分别为1、2、3、4阶岩土材料蠕变系数；k为岩体Abel黏性元件的本构参数；xk－1为虎克弹性体模型参数；wk为不同荷载下应力。 根据上述参数设计和拉薄膜效应、钢筋强度破坏准则，实现对建筑地基深基坑开挖底面变形风险预测和控制。

4.实验测试

为了验证本文方法在实现建筑地基深基坑开挖底面变形风险控制中的应用性能，进行实验测试。 建筑地基深基坑的高压缩性元件长140cm，桩长43.5m，采用4种盾构施工参数分别开挖500m，断面沉降值在5.2mm～5.3mm，开挖的盾构参数（ 如表2所示）:

表2 地基深基坑开挖的盾构参数

根据表2的参数设定，构建ANSYS有限元分析模型（ 如图3所示）:

图3 建筑地基深基坑开挖底面变形有限元分析结果

上述有限元分析结果能准确实现对地面变形的参数分析，得出衬砌结构及等代层参数（ 如表3所示）:

表3 衬砌结构及等代层参数

分析表3参数解析结果得知： 本文方法能有效实现对不同工况的底面变形风险预测。 测试预测的精度，得到对比结果（ 如图4所示）:

图4 风险控制精度对比

5.结束语

建立建筑地基深基坑开挖底面变形风险控制曲线分布模型，通过极限应力特征分析，实现构件的整体结构分析和风险控制。 本文提出基于弹性段—强化段为双折线拟合控制的变形风险控制方法。基于Maxwell体和Kelvin模型，进行时效变形行为特征分析， 采用Burgers蠕变模型进行Abel黏性元件的本构特征分析，实现对建筑地基深基坑开挖底面变形的结构参数模拟。 分析得出：用本文方法进行建筑地基深基坑开挖底面变形控制的参数解析能力较好，控制精度较高。