计及用户响应电价关联与多主体共赢的电动汽车充放电定价优化
2022-07-20董运昌刘世民曲朝阳宋佳骏薄小永
董运昌,刘世民,曲朝阳,3,宋佳骏,王 蕾,薄小永
(1. 东北电力大学电气工程学院,吉林吉林 132012;2. 国网内蒙古东部电力有限公司信息通信分公司,内蒙古呼和浩特 010000;3. 吉林省电力大数据智能处理工程技术研究中心,吉林吉林 132012;4. 广东电网有限责任公司广州供电局,广东广州 510000)
0 引言
面对能源危机与环境污染愈发严重的问题,电能推广将逐渐降低汽车领域对汽油、柴油等燃料的消耗,以缓解尾气排放带来的污染问题,使电动汽车(EV)成为未来交通领域的共同发展方向[1]。而EV的能源主要来自电网,其大规模发展离不开电力系统的支撑。据中国汽车工程协会预测[2],至2030 年我国EV 保有量将达到8 000 万辆,如果平均配备60 kW·h 的动力电池,则等效储能量将达到4.8×109kW·h,而我国2016 年的日上网电量仅为1.6×1010kW·h,无论是EV从系统吸收电能以满足能量需求,还是向系统释放电能,量级均是可观的。因此,合理的EV 用户充放电行为优化管理,可在电能短缺时为电网提供电能补给,达到电力供需平衡,对提高电网的安全稳定运行具有重大的意义。
随着车网互动(V2G)技术的发展,EV通过A/D和D/A装置既可以实现与电网的电能交换,也可以参与运营商充放电代理服务[3],从而实现用户与电网、运营商之间能量和信息的友好互动[4]。电网和运营商通过双向充放电装置配合电价优化策略与通信系统调控,使得EV用户在电网用电低谷时段选择充电以消纳电网过剩的电量,起到填谷的作用,并享受低谷时段低廉的电价[5];在电网用电高峰时段,作为分散式储能设备向电网提供电能,起到削峰的作用,并获得基于峰谷电价差的放电报酬[6]。因此,电网与运营商可以通过V2G 技术优化EV 用户的充放电行为,使更多的用户参与到电网调峰与调频、协调消纳新能源等服务中,为多个主体创造效益[7]。
通过调整电价的方式可以合理引导EV 用户分时段接入电网[8],国内外学者开展了部分相关研究:文献[9]通过分析用户的充电时长及模式,构建了一种引导EV有序充电的实时定价方案;文献[10]利用价格弹性理论对用户响应充电电价的方式进行分析,并利用分时电价策略调控EV 用户的充电行为;文献[11]考虑以充电电价浮动变化值和配电网电压安全期望值为约束,以充电站运营商期望收益最大化为目标对充电电价进行定价;文献[12]从电网经济利益角度出发,根据电网利益对EV的充放电定价进行优化;文献[13]结合对当前地区分时电价的划分,提出了一种两阶段有效充电策略方法。
目前已有较多关于EV 充放电定价优化方面的研究,但仍存在一定的局限性,主要表现为以下方面:①在电价优化方面,从充电、放电2 个维度兼顾多主体利益的研究较少;②在电价响应方面,对用户响应电价关联建模时,大多采用消费统计学或电力需求价格弹性分析进行关联建模,忽略了EV用户在响应电价时存在的响应饱和区及死区问题,难以体现不同消费用户在响应电价上的差异;③在多主体共赢方面,对峰谷充放电电价优化时大多强调引导用户降低电网负荷峰谷差以保证电网安全运行,忽略了用户满意度及运营商投入成本,导致用户响应电价的意愿不高涨及运营商成本增加的问题;④在多目标模型求解方面,针对定价优化模型的求解算法易陷入局部最优解,求解精度和效率有待进一步提高。
针对上述问题,本文计及用户响应与充放电电价的关联性,兼顾电网负荷峰谷差、用户满意度和运营商成本建立EV 充放电定价多目标优化模型。首先,构建了不同响应程度用户充放电转移与电价变化的关联模型,为运营商调整电价以引导用户有序充放电提供理论依据;然后,定义了单位投入成本函数,分析单位充放电能变化导致运营商新增投入成本的情况,并设计了以电网负荷峰谷差最小化、运营商节省成本最大化及EV 用户用电满意度最大化的多目标充放电定价优化模型,引导用户积极参与电网调控的充放电需求响应;最后,结合收缩空间和抗体适应度提出改进免疫鱼群算法,对定价模型进行优化求解,避免算法陷入局部早熟收敛,提高了最优解的精度和求解效率。
1 基于充放电负荷转移率曲线的用户响应电价关联分析
EV 响应电价的行为主要体现在负荷变化上,当电网稳定运行受到波动时,运营商通过激励策略或电价优化方案调整用户的用电结构,从而减少某段时间内的充放电负荷。因此,用户对电价的响应程度是运营商制定电价的依据。
1.1 采用局部加权最小二乘法拟合用户充放电负荷转移率曲线
根据用户的消费心理[13],将EV 用户对电价的响应方式分为正常响应状态(即线性区)、响应饱和状态(即饱和区)、无响应截止状态(即死区)3 种,每种响应方式都对应不同的负荷转移率曲线。为了求解不同的响应方式下用户充放电负荷转移率曲线,需确定曲线的斜率、饱和区阈值、死区阈值。将某天中时段a至时段b的充放电负荷转移率曲线表示为:

式中:Kab为负荷转移率曲线的斜率;lab为负荷转移率曲线的截距,即正常响应状态的阈值;hab为响应饱和状态的阈值;φmax为用户的最大负荷转移率;Δxab为时段a至时段b的电价变化量。
因此,基于EV 用户充放电峰转平负荷曲线、峰转谷负荷曲线、平转谷负荷曲线,拟合得到电价调整后含EV充放电负荷的电网日负荷Ls为:

式中:Lt0为电价调整前时段t含EV 充放电负荷的电网日负荷;Lv、Lf、Lp分别为谷、平、峰时段总负荷的平均值;Tv、Tf、Tp分别为谷、平、峰时段集合;φpf、φpv、φfv分别为峰时段到平时段、峰时段到谷时段、平时段到谷时段的负荷转移率。
为了求解用户充放电负荷转移率曲线的参数,本文采用最小二乘法,通过最小化充放电负荷的估计值与实际负荷间误差的平方和动态寻找充放电负荷转移率曲线的最佳拟合曲线参数,其拟合函数为:
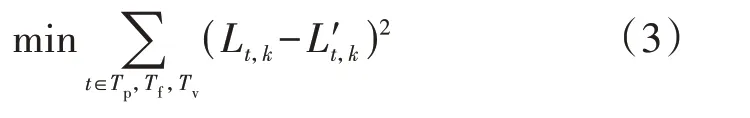
式中:Lt,k、L′t,k分别为第k次电价调整后时段t负荷的估计值、实际值。
基于此,可得第k次电价调整后,估计负荷转移率φk(x)与实际负荷转移率φ(x)的最小二乘拟合转移率参数模型为:
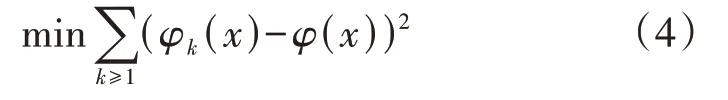
当EV用户规模较大时,采用最小二乘法计算将导致拟合目标函数扰动项的方差不全相等,存在异方差,使得拟合的参数值不是有效估计量,而是有偏的。为此,本文采用局部加权最小二乘法消除扰动项之间的异方差,使距离较近的点产生的影响大于距离较远的点产生的影响,加权因子ωk可表示为:
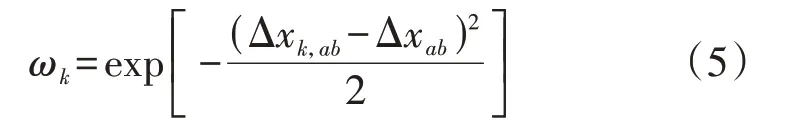
式中:Δxk,ab为第k次电价调整后时段a至时段b的电价变化量。
基于局部加权最小二乘法的拟合负荷转移率参数模型可表示为:

在电价调整之后反复拟合,得到充放电负荷转移率曲线的斜率、饱和区阈值、死区阈值,动态表征不同时段EV 用户的负荷转移率与电价变化量之间的关系。
1.2 不同用户响应电价程度关联分析
由于用户的消费心理存在差异,调整充放电电价将改变当前时段用户对充放电模式的选择。因此,根据用户响应电价的方式,对响应充电电价用户、响应充放电电价用户、不响应电价用户的充放电负荷转移情况进行分析。
1)响应充电电价用户分析。
假设EV 用户某天的行程被分为m段,其中第i(i=1,2,…,m)段行程包含n个时段。在用户的每一段行程时段内都存在停驶和行驶过程,而用户会根据实际情况选择在停驶过程中的时段j(j=1,2,…,n)对EV进行充放电。
在调整充放电电价后,响应充电电价的用户根据电价变化情况改变起始充电时刻和充电时长,并享受优惠电价。因此,在第i段行程中EV 将时段j的充电需求转移至优惠充电电价时段j+1的充电费用Qi,j+1可表示为:

式中:Ni,j为第i段行程中时段j行驶的EV数量。
2)响应充放电电价用户分析。
在调整充放电电价后,参与V2G 放电的EV 用户也会响应放电电价使得收益最大化。因此,对于响应充放电电价用户而言,在放电过程中需保证其电量能满足下一段行程需求,且其在前一充电时段的充电费用需要小于下一放电时段的收益。则EV用户在第i段行程中时段j+1 放电所获总利润可表示为:

式中:Qi,j-1为第i段行程中EV 从时段j-1 开始充电至时段j开始放电过程中的充电费用。
由于用户存在放电利润要高于充电费用的心理,所以在第i段行程中需满足时段j至时段j+1(时长为ti,j)放电所获利润不小于时段j-1 至时段j(时长为ti,j-1)的充电费用,即:

3)不响应电价用户分析。
在调整电价后,不响应电价用户既不改变充电时刻,也不参与V2G 放电,其充放电行为与电价调整前并无区别。因此,不响应电价用户的充放电负荷变化与电价调整无关,对于不响应电价用户而言,如果其不响应充电电价,则一定不会响应放电电价。因此第i段行程中时段j不响应电价用户的数量为:

2 计及用户电价响应的多主体共赢充放电定价多目标优化模型
在调整充放电电价后,EV 用户会根据实际情况调整自身的充放电方式即充放电时间,以平衡充电费用与放电收益。但是,如果运营商在调整电价时只保证电网与运营商的利益最大化,则会影响用户参与响应电价的满意度,从而拒绝接纳优化方案,影响优化方案的正常实施;如果在调整电价时只考虑用户用电满意度最大化,则会提高运营商的投入成本,并增加电网负荷。因此,计及用户响应电价的不同情况,本文建立了考虑电网负荷峰谷差最小、运营商节省成本最大及用户用电满意度最大的充放电定价多目标优化模型。
2.1 优化目标
1)电网负荷峰谷差最小化。
电网公司的利益目标为:在调整电价以改变用户充放电习惯时,能最小化系统的峰负荷及负荷峰谷差。用户响应电价的程度越高,则越容易调节电网负荷峰谷差。因此,电网公司的目标函数为:

式中:G1为峰负荷;G2为负荷峰谷差;L*t0为时段t不包含EV负荷的原日负荷。
2)运营商节省成本最大化。
运营商的利益目标为把控投入成本,投入成本包括固定成本、可变成本,其中固定成本为充电站内充电桩的建设成本,可变成本为充放电过程中电能损耗、电池寿命损耗的折算成本。在运营商固定成本不变的条件下,应尽量减少可变成本,从而减少运营商的总成本支出。一般意义上的电能损耗成本为电网在生产电能时需要消耗的成本,而本文定义EV在电网充放电过程中的单位电能损耗成本ce为:

式中:cEL为在充放电过程中由于能量转换所导致的单位电能损耗成本。
电网负荷均方差反映了电网负荷的波动性情况,均方差越大,则波动性越大,其是影响电能损耗成本的重要指标。最小化日负荷均方差的目标函数可表示为:
式中:G3为日负荷均方差;Lav为EV 响应调度后的日平均负荷。
在调整峰谷充放电电价后,可减少EV在峰时段集中充放电导致的系统负荷波动和电能损耗成本,则运营商的目标函数可表示为:

式中:Ccost为运营商节省成本;L′EV为电价调整后的EV平均总负荷,其与用户响应电价的程度紧密关联。
3)EV用户用电满意度最大化。
为了避免新增运行成本,充电站运营商与电网公司对峰谷充放电电价进行调整,但电价变化会引起用户用电方式发生较大幅度的改变,会影响用户用电舒适度,导致其满意度下降,从而降低用户响应电价的能力。因此,从用户角度出发,在调整电价的同时需要保证用户用电满意度最大,本文的用电满意度包括响应电价的满意度、用户参与充放电调度的等待时间。与响应电价前、后电网总负荷变化和等待时间相关的用户用电满意度目标函数为:
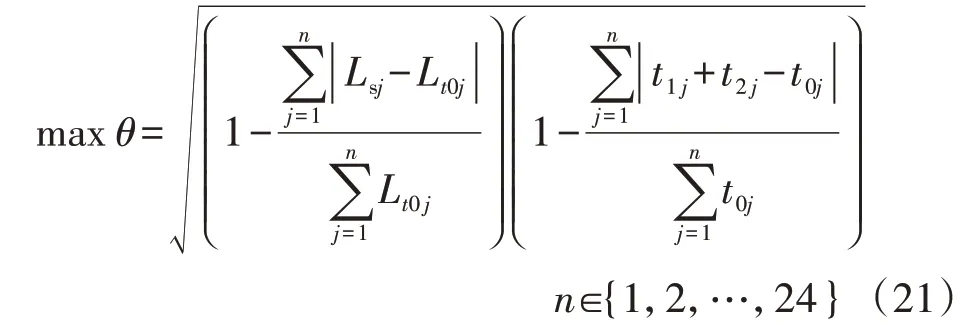
式中:θ为用户用电满意度;Lsj为调整电价后时段j含EV负荷的电网负荷;Lt0j为调整电价前时段j的电网负荷;t1j、t2j分别为调整电价后时段j的EV 充电等待时长、放电等待时长;t0j为调整电价前时段j的EV充放电等待时长。
2.2 约束条件
约束条件包含EV行程里程约束、电池电量状态约束、充放电时间约束、V2G放电电价约束。
1)EV行程里程约束。
EV 在向电网放电后的剩余电量需满足下一段行程的电量需求,且放电量应介于电池容量的最大值和最小值之间,即满足:

式中:Ss为EV电池的荷电状态,为电池剩余电量与电池容量CB的比值,取值范围为[0,1];Smax、Smin分别为EV 电池荷电状态的最大值、最小值;di+1为第i+1段行程的行驶距离;W为EV 行驶1 km 的电池平均耗电量。
2)电池电量约束。
EV 在进行充放电的过程中,应保持其充放电电量在电池的最大电量与最小电量之间,即需要满足:

3)充放电时间约束。
在停驶过程中EV 的充放电时间应不大于前一段行程的行驶时长与后一段行程的行驶时长之差,且充放电时长非负:

另外,用户可在某一时段选择对EV进行充电或放电,但充电过程与放电过程不能同时进行,即满足:

4)V2G放电电价约束。
根据运营商的成本和放电收益,将EV参与放电的固定成本折算为单位电量成本cf,则EV 参与V2G放电的电价应满足:

2.3 多目标优化模型
综上所述,基于EV 用户响应电价的情况,在满足EV充放电习惯及电池特性的约束条件下,综合考虑电网负荷峰谷差最小化、运营商节省成本最大化和用户用电满意度最大化,建立协调用户、电网与运营商之间利益的充放电定价多目标优化模型,如式(29)所示。

式中:F(x)为多目标优化目标函数;x为优化变量向量;Uk(x)为不等式约束条件函数;q为不等式约束条件数量。
3 基于收缩空间的免疫鱼群算法求解模型
在保证电网负荷峰谷差、峰负荷最小化的目标下,要使用户用电满意度最大化和运营商节省成本最大化,显然这3 个目标函数之间存在互斥矛盾关系,而多目标优化是均衡各目标函数的解以找到满足条件的最优解。因此,在解决多目标优化问题时,本文设计了基于收缩空间的多目标免疫鱼群算法(CSMOIFSA)。凭借人工鱼群算法动态求解收敛速度快的优势对充放电定价多目标优化模型进行求解,并引入免疫算法解决算法容易早熟收敛至局部劣解的问题。
3.1 CSMOIFSA
1)基于收缩空间的免疫抗体浓度计算。
采用距离矢量的方法减小搜索空间,规避了信息的重复计算,相邻点存储了到当前点的最优距离解,避免在迭代求解时重新计算已经迭代过的点,降低了信息计算的复杂度。计算过程见附录A 式(A1)—(A6)。
2)结合免疫抗体适应度的鱼群寻优方法。
由于人工鱼群算法在优化求解后期会出现鱼群趋同导致优化结果陷入局部解的问题,本文引入免疫算法产生多种抗体以保持进化群体的多样性,避免算法早熟收敛至局部劣解。计算过程见附录A 式(A7)—(A9)。
3.2 充放电定价多目标优化模型的求解步骤
CSMOIFSA 是在原有算法所得多个解中寻找更优的Pareto 解集,使得在其他目标下非劣最优解函数构成非劣最优目标域,从而解决多个目标函数相互制约的问题。多目标优化模型的求解步骤如下。
步骤1:初始化参数。输入EV 电池参数、用户充放电负荷转移率曲线参数的初始值。
步骤2:初始化多目标免疫鱼群算法。在求解空间内随机初始化H个抗体(即个体人工鱼),设定个体人工鱼的维度为峰平谷充放电电价,每条个体人工鱼对应不同时段的充放电电价,生成人工鱼群规模M、最大迭代次数K。
步骤3:确定目标函数。将充放电定价多目标优化模型的目标函数F(x)与不等式约束条件函数Uk(x)作为抗原,并采用分层聚类法对种群进行分层,将每一层中所有个体人工鱼赋值到初始Pareto解集公告板中。
步骤4:寻优过程。通过模拟人工鱼的生物行为,选择在人工鱼群觅食过程中行为最优的人工鱼,更新个体鱼。
1)觅食行为。在第i条人工鱼当前位置xi的随机视野范围内的另一位置x(j即‖xi-xj‖2<V,V为视野范围),判断是否满足Yj>Y(iYi、Yj分别为位置xi、xj处的食物浓度),若满足,则人工鱼个体向位置xj移动;否则,再次随机选择下一位置xj。反复判断下一位置是否满足移动条件,如果仍不满足移动条件,则随机向前移动。
2)追尾行为。计算在第i条人工鱼当前位置xi的随机视野范围内的伙伴数量nf,找到伙伴中寻食的最优位置xbest,若满足Ybest/nf>δYi(Ybest为最佳位置的食物浓度,δ为拥挤因子),则说明处于位置xbest处鱼群的拥挤程度低且周围食物的浓度高,向位置xbest方向移动;否则,执行觅食行为。
3)聚群行为。计算在第i条人工鱼当前位置xi的随机视野范围内的伙伴数量nf及其中心位置xcenter,若满足Ycenter/nf>δYi(Ycenter为中心位置的食物浓度),则向中心位置xcenter方向移动;否则,执行觅食行为。
步骤5:评价所有抗原与抗体(人工鱼)之间的亲和度,选取亲和度最高的个体鱼赋给公告板,更新Pareto最优解外部公告板。
步骤6:判断是否满足最大迭代次数,若满足,则输出最优峰谷充放电电价解集,停止迭代;否则,转至步骤3。
4 实验算例与分析
4.1 实验数据与参数设置
1)EV电池参数。
由于EV电池种类较多,本文主要以车载动力电池占比较高的尼桑与比亚迪EV 分别采用的锂离子电池和磷酸锂铁电池(分别记为NS 电池和BYD 电池)为基础进行分析,其主要参数[14-15]见附录B表B1。在EV 充放电过程中,设定其电池的最小荷电状态Smin=15%,最大荷电状态Smax=95%;电池的充电效率ηup、放电效率ηdown均为97%;电网电能转换效率η=85%;电池的充电电量系数λdown、放电电量系数λup均为0.1。根据目前比亚迪和尼桑EV 的占有量[16],设定2 种类型EV 的数量之比为0.57∶0.43,按照该比例抽取不同类型EV 数量进行仿真,EV 放电功率Pup、充电功率Pdown均为6.75 kW,CB=40.5 kW·h,W=0.182 kW·h/km。
2)初始充放电电价及负荷数据。
历史负荷数据采用PJM 美国能源市场某一天的实时负荷数据[17],电价采用加州电网的峰谷分时电价数据[18],当天的历史负荷数据及分时充放电电价分别如附录B 表B2 和表B3 所示。由于本文多提定价模型需要基于海量用户的实时响应情况,在实际运营过程中需要考虑较为复杂的数据体量,根据目前美国加州623.4万辆的私家车保有量[19],假设加州地区EV的接入数量为300万辆。
3)用户转移率初始化参数。
根据用电用户的调查情况[20-21],设定用户转移率曲线初始值参数如附录B 表B4 所示,并通过优化更新用户转移率参数。
4)EV用户出行习惯数据。
根据文献[22]所提EV 充电功率需求的统计学建模方法可知,EV 用户起始出行时刻分布fs(τ)满足正态分布τ~N(17.47,3.412 2),而EV用户的日行驶里程fD(s)满足对数正态分布lns~N(3.46,1.142 2),起始荷电状态满足正态分布N(0.4,0.12)。计算第i段行程中时段j到下一时刻k行驶距离为l(单位为km)时进行充电或放电的EV数量为:
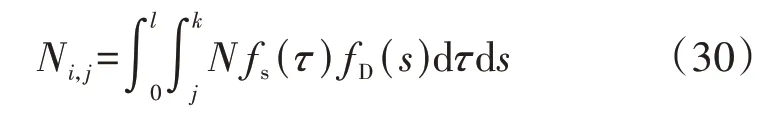
式中:N为当前EV的总数量。

根据上述关系,采用文献[22]所提EV充电负荷计算方法进行蒙特卡罗随机抽取,生成单个EV用户一的充放电计划(包括一天内的行驶里程、起始出行时刻、荷电状态),计算单个用户的充放电负荷,进行叠加可得到规模化EV的充放电负荷曲线。
4.2 CSMOIFSA验证
为了测试CSMOIFSA 的性能,本文选取ZDT测试函数集进行测试验证。ZDT 测试函数在评价多目标算法时具有较好的分布性与收敛性,选取带有2 类目标函数,且每个Pareto 解集前沿均已知,其测试函数见附录B 式(B1)和式(B2)。对多目标人工鱼群算法(MOAFSA)和本文所提CSMOIFSA 最优解的收敛性、均匀性和误差比进行定量分析,3 个指标的计算公式分别见附录B式(B3)—(B5)。
仿真初始化参数设置如下:视野范围V=0.5,鱼群规模M=100,最大迭代次数为100,拥挤因子δ=0.25。算法在仿真计算过程中存在随机性,使得模拟结果之间存在偏差,因此在仿真过程中每个计算过程均单独运行30 次,取其平均值,记录运行结果。2 种算法的3 个指标计算结果分别如附录B 表B5—B7 所示。由表可知:2 种算法的Pareto 最优解的收敛性相差不大;CSMOIFSA 的均匀性指标结果明显优于MOAFSA,其均匀性指标值下降了18.39%;相较于MOAFSA,CSMOIFSA 的平均误差减少了11.9%。可见,2 种算法在收敛性上相差不大,但是CSMOIFSA 拥有更好的Pareto前沿解分布,且其误差比更小,更接近真实值。
4.3 多目标优化模型结果分析
在Python3.8 平台进行仿真验证,算法参数设置同4.2 节。采用CSMOIFSA 对EV 充放电定价多目标优化模型进行求解,每次优化后根据EV响应与电价关联模型计算调整电价后用户的负荷变化情况。运营商的节省成本与电网负荷峰谷差随用户用电满意度的变化曲线如图1所示。
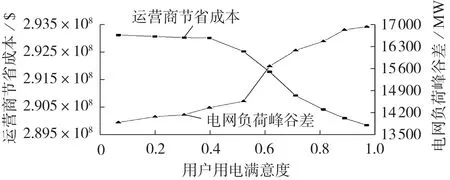
图1 运营商节省成本与电网负荷峰谷差随用户用电满意度的变化曲线Fig.1 Change curves of cost saving of operators and peak-valley load difference of power grid vs.power consumption satisfaction degree of users
由图1 可知,运营商节省成本、电网负荷峰谷差与运营商和电网公司的利益有关,运营商节省成本随着用户用电满意度的增加逐渐减少,电网负荷峰谷差随着用户用电满意度的增加逐渐增大,这是因为:在没有调整电价的情况下,用户的行为习惯没有发生改变,用户不会通过响应充放电电价来平缓电网负荷峰谷差;而当优化运营商节省成本和电网负荷峰谷差时,会对用户用电满意度产生影响。当用户用电满意度在0.65~0.85 范围内时,运营商节省成本与电网负荷峰谷差的调节程度最大,因此在该范围内的Pareto 解使得用户响应电价的能力较高。对比单一目标优化模型,将电网负荷峰谷差最小作为优化的共同目标,分别以用户用电满意度最大和运营商节省成本最大为目标,在Pareto 解集中搜索极端解,结果如表1所示。

表1 Pareto解集中的极端解Table 1 Extreme solutions in Pareto solution sets
由表1 可知:若仅以用户用电满意度最大为目标,则会增加运营商的投入成本;若仅以运营商节省成本最大为目标,则会降低用户用电满意度,进而降低其响应电价的能力,使得电网负荷峰谷差加大。计算极端解下不同响应用户的充放电负荷变化情况,结果如图2所示。

图2 极端解下不同响应用户的充放电负荷变化情况Fig.2 Charging and discharging load changes of different response users under extreme solutions
由图2 可知:在以用户用电满意度最大为目标的情况下,EV 用户根据自身的利益需求进行充放电,使得用户都集中在峰时段与谷时段向电网充放电,增加了峰谷时段电网安全运行的压力;而在以运营商节省成本最大为目标的情况下,运营商为了调节负荷,减少负荷峰谷差与投入成本,大幅调整峰、谷时段的电价以吸引用户充放电,使得响应充电电价的用户向平时段和谷时段转移,响应充放电电价的用户集中在峰时段放电,导致用户的充放电方式发生大幅度变化,但此时的用户用电满意度较低;在以电网负荷峰谷差最小为目标的情况下,积极引导用户进行有序充放电,用户的充放电习惯容易受到影响而导致用电满意度不高,且在进行充放电行为交互过程中运营商投入成本也相应增加。
因此,为了协调电网公司、充电站运营商和用户三方的利益,在其他目标不为局部劣解的情况下,采用CSMOIFSA 求解式(29),本文根据文献[23]的模糊隶属度函数计算Pareto 解集中的用户用电满意度,选择用户用电满意度最大的解作为最优折中解,结果为:θ=0.82,Ccost=$2.8685×108,G1=14021.5 MW,G2=91 213.7 MW,G3=2 009 690.6 MW2。最优折中解下的充放电电价如表2所示。

表2 最优充放电电价Table 2 Optimal charging and discharging prices 单位:¢/(kW·h)
根据最优折中解计算调整电价前、后电网日负荷、运营商投入成本、用户用电满意度,结果如图3所示。由图可知:相较于调整电价前,调整电价后的电网峰负荷减少了1719.45 MW,负荷峰谷差减少了3 564.31 MW;对EV 充放电电价进行调控后,运营商节省了投入成本,最大节省成本达到$2.988 7×108,最小节省成本为$2.866 6×108;调整电价后,用户用电满意度得到提高,且用户用电满意度变化趋势与运营商节省投入成本反相关,即运营商节省成本越大,则用户用电满意度越小。

图3 调整电价前、后的结果对比Fig.3 Comparison of results before and after adjusting electricity price
多目标优化下不同响应用户的负荷曲线如图4所示。由图可知,多目标优化后峰时段负荷减少,选择峰时段充电的用户开始向平时段和谷时段转移,使得系统负荷波动性变缓,负荷峰谷差减小。响应放电电价用户在系统负荷高峰时段向电网放电,缓解了EV接入后对充电负荷的需求,且响应充电电价用户在谷时段和平时段改变自身的充电时刻,减少了高峰时段的充电负荷需求压力。
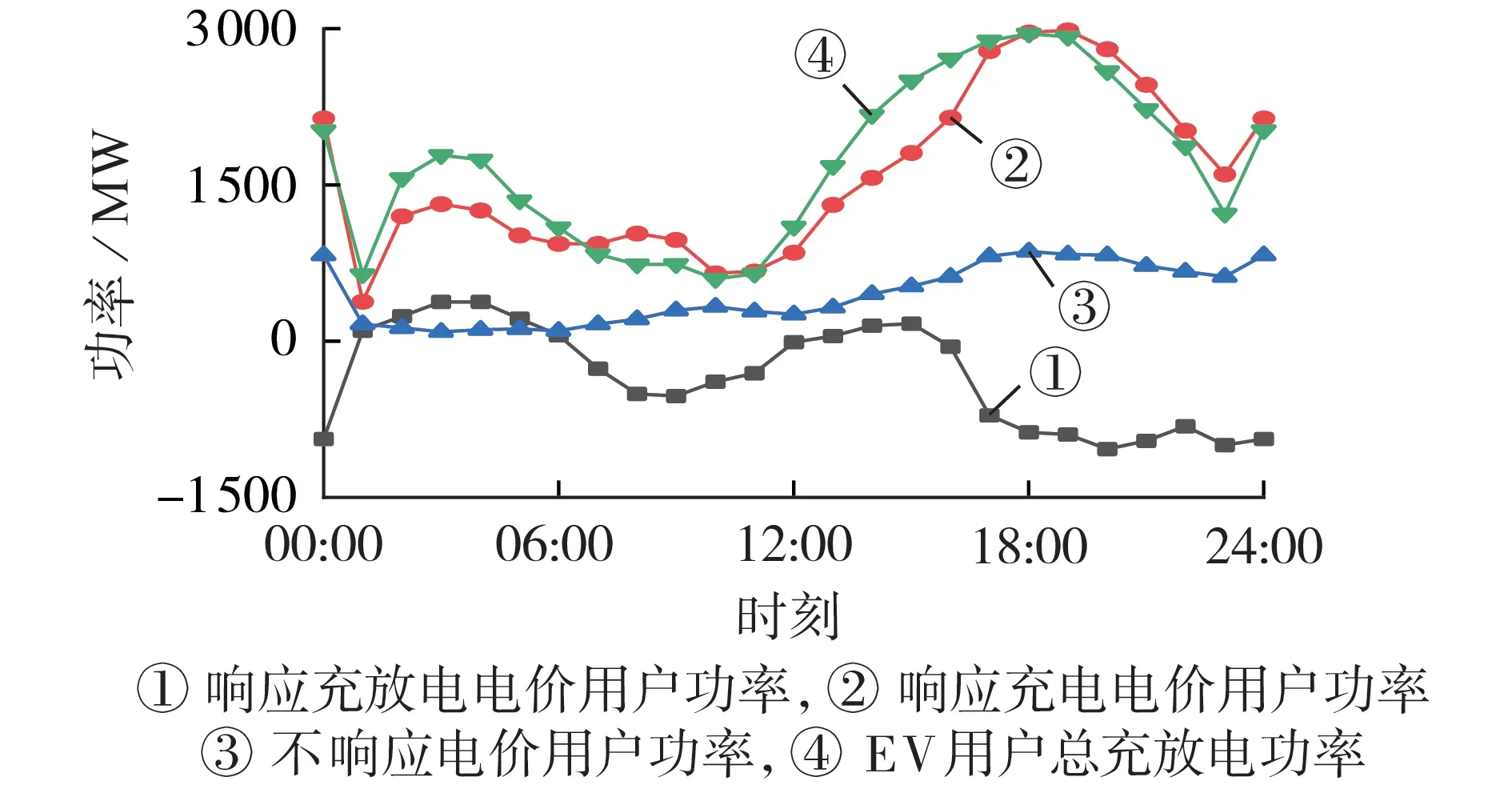
图4 多目标优化下不同响应用户的负荷曲线Fig.4 Load curves of different response users under multi-objective optimization
综上所述,若在求解充放电电价时只保证其中一个目标最优,则将导致其他目标陷入劣解。而在充放电电价多目标优化模型下,电网公司、充电站运营商和用户三方利益得到协调,在满足电网峰负荷和峰谷差最小的条件下,运营商投入成本减少,用户用电满意度增加,使得更多的用户参与电价优化过程,最终实现了基于充放电电价多目标优化方法引导用户有序充放电,达到“削峰填谷”的目的。
5 结论
针对EV 用户响应充放电电价时存在的不确定行为,本文提出了计及用户响应电价关联和多主体共赢的EV充放电定价多目标优化方法,基于算例仿真分析得到以下结论:
1)同时考虑引导用户行为的分时段充电和放电电价,设计峰平转移率、峰谷转移率和平谷转移率下的响应充放电策略更为合理;
2)通过用户响应电价下的多目标优化模型,可以实现电网负荷峰谷差、运营商节省投入成本和用户用电满意度的均衡优化,达到多主体共赢的目的;
3)所提CSMOIFSA 提高了模型的求解精度,通过美国加州地区大规模EV 的算例分析验证了改进算法适用于求解较大EV规模的实时调度决策问题。
附录见本刊网络版(http://www.epae.cn)。
