计及可再生能源可靠性的虚拟电厂动态聚合方法
2022-07-20白雪岩樊艳芳王天生刘雨佳聂昕磊颜晨煜
白雪岩,樊艳芳,王天生,刘雨佳,聂昕磊,颜晨煜
(1. 新疆大学电气工程学院,新疆乌鲁木齐 830017;2. 中国能源建设集团新疆电力设计院有限公司,新疆乌鲁木齐 830000;3. 国家电网有限公司技术学院分公司,山东济南 250000)
0 引言
作为碳达峰的关键时期,“十四五”期间我国将持续推动可再生能源的大规模开发与利用,构建清洁低碳安全高效的现代化能源体系[1-2]。但受地形、地势、气候条件以及机组自身等随机因素的影响,可再生能源出力呈现不确定性[3],使得可再生能源发电系统的可靠性[4]大幅降低,导致电网调度中心对可再生能源制定的计划发电量以及对可再生能源调度的积极性都大幅下降。虚拟电厂VPP(Virtual Power Plant)技术是将不同类型的能源聚合,通过高效的能源管理优化方案,提高VPP整体可靠性,使电网对其下达更多的发电计划。
当VPP 可靠性较差时,会加剧常规能源对可再生能源的挤出效应,致使电网对可再生能源供电能力的信任度下降,弃风弃光现象严重。由此可见,VPP 的可靠性评估不仅是其能否参与电网调度的重要参考依据,还是本文所提VPP 动态聚合模型的基础。现阶段,对于VPP 可靠性的探讨已取得了一些成果,文献[5]对仅由风电机组构成的VPP进行可靠性评估;文献[6-7]在评估由风电机组和光伏机组构成的VPP可靠性时,将不同机组的可靠性指标求和,作为VPP 的可靠性指标,但该方法粗略地将不可同度量的机组进行同质化处理,导致可靠性指标的计算精度下降,造成资源大量浪费。
目前,对于静态VPP 积极参与电网运行调度的研究也取得了一些成果。文献[8]将风电机组、光伏机组、柴油机组构成VPP系统,利用柴油机组调配合风电机组和光伏机组出力,从而更好地满足负荷需求,配合电力市场协同调度。文献[9]构建了风电场结合电池储能系统的VPP 优化调度模型,利用电池储能满足系统功率动态平衡需求。文献[10]构建了含风力发电、光伏发电、燃气轮机、抽水蓄能和储能电池的VPP 经济优化调度模型,通过抽水蓄能和储能电池联合运行补偿出力偏差,使VPP 实际出力能更好地跟踪计划出力。文献[11]考虑引入电动汽车,利用电动汽车的充放电特性平衡VPP 输出的随机变化。文献[12]使用抽水蓄能解决风电机组和光伏机组出力不确定性问题,以达到VPP 整体利润最大化的目的。上述文献中构建的VPP 即静态VPP,大多都是在风电场和光伏电站已经聚合好的基础上,灵活调控储能等其他形式的可控电源,调节VPP出力,进而实现各自目标。该方法不仅未充分挖掘可再生能源自身潜力,而且容易造成储能等其他形式可控电源的容量配置过大,导致资源浪费。
VPP 的动态聚合模型具有线性与非线性关系混合、计算量大、条件复杂等特点,需在算法选取方面进行进一步研究。文献[13]采用模拟退火算法对模型进行求解,该算法计算过程简单,适用于求解复杂的非线性优化问题,但其收敛速度较慢并且求解精度和速度受初值影响较大。文献[14-15]分别利用粒子群优化PSO(Particle Swarm Optimization)算法、人工蜂群算法求解目标函数最优解,这些算法都具有较快的求解速度,适用于求解连续函数优化问题,但在求解过程中容易产生早熟收敛、陷入局部最优等问题。而文献[16]提出的光线寻优LRO(Light Ray Optimization)算法是一种基于费马原理,通过模拟光在变折射率介质内通过反射与折射不断变化方向的过程中寻得最佳传播路径的新型智能优化算法,具有很好的收敛性、稳定性,能够在要求的精度范围内较快地收敛到目标函数的最优值,具有很高的工程应用价值。此外,LRO 算法的随机性要远远大于上述算法,能够在要求的精度范围内较快地收敛到目标函数最优值且不会陷入局部最优解。但该算法无论是在求解维度方面还是在计算速度方面都存在明显不足。为此,文献[17]提出无网格光线寻优(FLRO)算法提高了二维目标函数的收敛速度,但在求解多维目标函数的优化问题时,上述算法依然不适用。因此本文对FLRO 算法在计算维度方面进行改进,具有重要意义。
综上所述,本文提出一种计及可再生能源可靠性的VPP 动态聚合方法。首先对风电、光伏的出力模型进行分析和修正;其次,将不同机组进行同质化处理,建立考虑置信容量的VPP可靠性评估模型;然后,以电量不足期望值最小为优化目标,构建计及可再生能源可靠性的VPP 动态聚合模型,并采用改进无网格光线寻优(IFLRO)算法对该模型进行求解;最后,以新疆某区域负荷数据为算例,通过仿真验证了所提方法的可行性、高效性与稳定性。
1 考虑元件停运概率的可再生能源出力模型
可再生能源出力主要受当地气候因素的影响,这种影响使其出力具有不确定性的同时呈现出季节特性[18]。此外,可再生能源作为构成VPP 的主要元素,其出力的不确定性会对模型计算的准确度产生较大的影响。因此,本文构建可再生能源出力模型并进行修正,为后续VPP 可靠性的评估以及VPP 动态聚合模型的求解提供更准确的参数。
风速的变化受多种因素共同影响。文献[19]通过气候倾向率分析法对西北地区风速进行分析,得到了影响风速变化的因素以及风速变化特征。风机输出功率与风速之间的关系可参考文献[20]。对于西北地区而言,风电机组表现出较强的季节特性,其平均出力呈现出春冬季较大、夏秋季较小的特点。地球公转引起太阳高度角变化,致使不同季节的太阳起落时间以及大气上界辐照强度差异明显,导致光伏出力的持续时间和最大值发生变化。光伏输出功率与光照强度之间的关系可参考文献[21]。对于西北地区而言,光伏平均出力呈现的季节特性为夏秋季较大、春冬季较小。
可再生能源发电系统内部任何一个环节的设备发生故障,都可能影响最终出力。本文将综合构成风机所有部件的停运概率作为其整体的停运概率,对光伏出力单元的停运概率的处理方法与其类似。当光伏发电单元发生故障时,一般是其内部少数太阳能电池板发生故障,对于1 个包含上百个太阳能电池板的光伏发电单元而言,其影响是微乎其微的。为此,本文将10 个光伏发电单元视为1 个光伏出力单元,将1台风机视为1个风电出力单元。
对于光伏电站或风电场而言,将每一个光伏出力单元或风电出力单元视为在运行和故障间不停转换的两状态单元。分别用工作时间t1和修复时间t2描述元件在各个状态的持续时间。一般认为工作和修复时间均服从指数分布,通过抽样可得到各元件的时序状态分布如下:

式中:η、μ分别为元件的故障率和修复率;γ为服从[0,1]均匀分布的随机数。
将得到的元件时序状态分布序列按照时间顺序修正风电、光伏出力序列,可得到考虑元件停运概率的可再生能源发电系统出力模型,其中风电场、光伏电站时序状态分布图分别如附录A 图A1 和图A2所示。
2 VPP可靠性评估
当前,有关VPP 可靠性评估的研究在电力系统获得了广泛关注。为此,本文首先对单个风电场、光伏电站的可靠性进行评估,然后将置信容量引入VPP 可靠性评估中,最后构建考虑置信容量的VPP可靠性评估模型。在评估过程中,假定单位小时内机组出力和负荷功率均保持不变。
2.1 风电场、光伏电站的可靠性评估方法
本文利用序贯蒙特卡洛法评估风电场、光伏电站的可靠性。选取电力不足时间概率、电力不足时间期望、电量不足期望值3 种可靠性指标[22],分别从停电概率、停电时间以及停电电量方面评估风电场、光伏电站的可靠性。在上述可靠性指标中,电量不足期望值综合描述了停电次数、平均持续时间和平均停电功率,因此,本文将电量不足期望值作为主要参考指标,其余指标作为辅助参考指标。上述各个指标的物理含义如下。
单个风电出力单元、光伏出力单元的电力不足时间概率表达式为:

式中:δLOLP为电力不足时间概率;pl为处于系统状态l时发生停运的概率;tl为处于系统状态l时发生停运的时长。当机组容量不满足负荷需要时,该指标可判断电力系统的停电时间概率,但未考虑停电量的大小。
单个风电出力单元、光伏出力单元的电力不足时间期望表达式为:
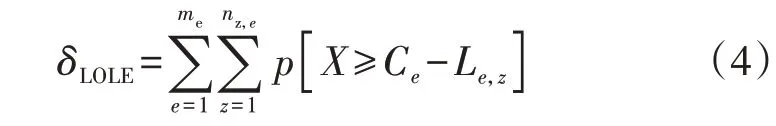
式中:δLOLE为电力不足时间期望;p[X≥Ce-Le,z]为第e个时间段第z天机组停运容量大于等于备用容量的概率,Ce为第e个时间段系统的装机容量,Le,z为第e个时间段第z天的负荷峰值;me为一年中的时间段数;nz,e为第e个时间段中的天数。该指标可判断电力系统机组停运容量大于等于备用容量的概率。
单个风电出力单元、光伏出力单元的电量不足期望值表达式为:

式中:δEENS为电量不足期望值;PI(X)为第I个小时机组停运容量大于等于I的概率;CI为第I个小时系统中的装机容量;LI为第I个小时的负荷;T为模拟小时数。该指标反映了电力系统由于机组受迫停运而对用户减少供电的期望值。
风电场、光伏电站的可靠性评估是在计算得到单个风电出力单元、光伏出力单元时序状态分布的基础上,再将场站内所有风电出力单元、光伏出力单元的时序状态分布累加,最终得到单个风电场、光伏电站的时序状态分布,根据该时序状态分布计算单个风电场、光伏电站的可靠性指标。
单个风电场、光伏电站的可靠性指标的计算公式为:

2.2 VPP的可靠性评估方法
风电、光伏出力特性差异较大且属于不同类型机组导致不能直接将确定常规机组可靠性指标的方法用于VPP的可靠性评估。而置信容量这一指标不仅可将风电场、光伏电站等效成同种类型的常规电厂,而且其数值大小反映了不同风电场、光伏电站比拟常规电厂的能力。因此,本文考虑利用置信容量计算VPP可靠性指标。置信容量的概念是在等可靠性的前提下,将风电场或光伏电站替代常规机组容量的大小用于评估该电场或电站的置信容量。该指标不仅可以描述风电场、光伏电站的容量价值,还可用于量化风电场、光伏电站对电力系统充裕度的贡献。
为了提高VPP 置信容量的计算效率,本文利用辅助函数法计算风电场、光伏电站的置信容量,求解步骤如下[22]。
步骤1:利用序贯蒙特卡洛法计算得到风电场、光伏电站的可靠性指标δEENS。
步骤2:根据风电场和光伏电站装机容量CN的不同,可得到对应的可靠性指标,从而绘制得到风电场和光伏电站的δEENS-CN曲线,分别如附录B 图B1和图B2所示。
步骤3:用风电场替代常规机组,根据常规机组装机容量Cr的不同,可得到对应的可靠性指标,绘制风电场替代常规机组的δEENS-Cr曲线,光伏电站替代常规机组的δEENS-Cr曲线可同理获得。
步骤4:当风电场容量为CN0时,首先在δEENS-CN曲线上找出与风电场容量CN0对应的可靠性指标δEENS0,然后根据该值在δEENS-Cr曲线上找出对应的容量Cr0,该Cr0值即为风电场的置信容量,光伏电站的置信容量可同理获得。
风电场、光伏电站的置信容量计算公式为:

式中:δEENS(·,·)为电量不足期望函数;Ls为系统负荷。
所有风电场、光伏电站总的置信容量计算公式为:

式中:Call为所有风电场、光伏电站总的置信容量;M为所有风电场、光伏电站的数量;Cu为第u个风电场或光伏电站的置信容量。
VPP的可靠性指标计算公式如下:

将式(9)代入式(10)可得:

在实际应用中,由不同类型能源构成的VPP,其可靠性可通过该方法进行评估。VPP 可靠性指标的计算流程如图1所示,图中N为样本数。
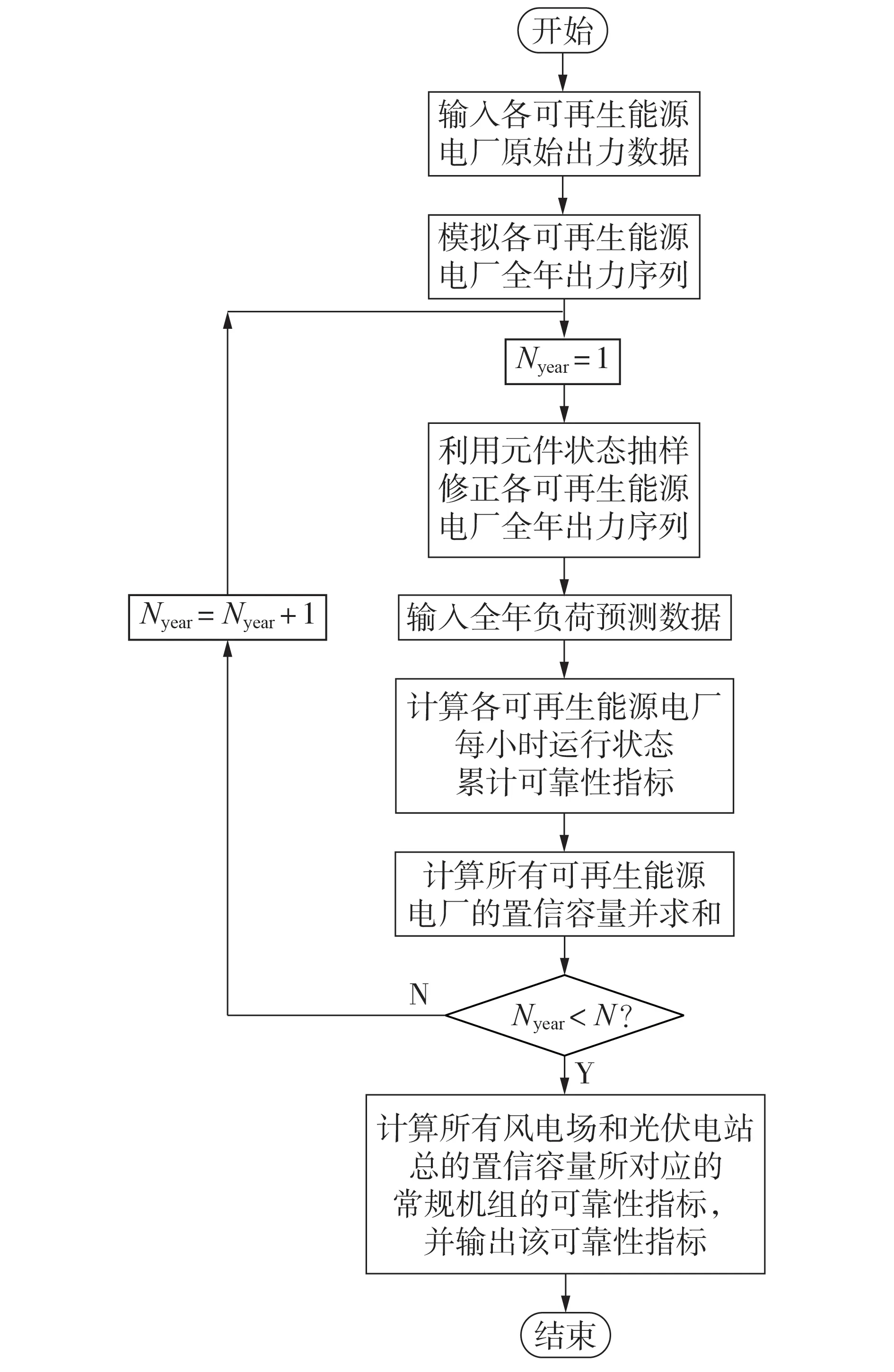
图1 VPP整体可靠性指标计算流程图Fig.1 Flowchart of overall reliability index calculation for VPP
3 考虑可再生能源出力可靠性的VPP 动态聚合模型
可再生能源出力的季节性和不确定性导致电力系统事故常发,对整个社会的经济造成极坏影响;同时,还会对电网调度产生一定的阻力,致使电网调度可再生能源的积极性下降。而本文提出的考虑可再生能源出力可靠性的VPP 动态聚合模型,改善了VPP 由于其供电可靠性较差,导致电网对其调度的积极性不高,使得可再生能源消纳量较低的问题。
本文以某一季度为研究周期,直接对某区域内风电场、光伏电站按照指定原则进行聚合来参与电网的调度。该方法将采用本文构建的VPP可靠性指标——电量不足期望值最小作为其动态聚合模型的优化目标。对风电场、光伏电站进行动态聚合不仅可以降低其出力的季节性和不确定性对供电能力的影响,还可以在提升上网电量的同时,进一步提高VPP整体的灵活调控能力,减少资源浪费。
3.1 目标函数
本文以电量不足期望值最小为目标,利用智能算法寻找到满足目标函数的最优组合。目标函数如下:

式中:Su为表示第u个风电场或光伏电站是否参与聚合的0-1变量,Su=1表示参与聚合,Su=0表示不参与。
3.2 约束条件
1)电力系统功率平衡约束。

2)风电出力单元运行约束[23]。

3)光伏出力单元运行约束。

4)弃风弃光率约束。

4 IFLRO算法
4.1 FLRO算法在求解多维目标函数中的改进


式中:sign(·)为符号函数。
否则,光线进行反射。向n个试探点中传播速度最小值所对应的传播方向进行反射,计算公式如下:
3.猪繁殖与呼吸综合征。LSI猪繁殖和呼吸综合征抗体检测试剂盒,有效期至2011年5月,购自上海天之泰生物科技有限公司。试剂盒使用前恢复至室温,对血清样品用样品稀释液进行1:200倍稀释然后取50 μl经稀释后的样品血清加入反应板中(阴阳性对照不用稀释),盖上膜,将反应板放置在37℃下孵育60 min后,用300μl洗涤液洗涤3次拍干,加入50 μl酶标抗体,37℃孵育60 min后再洗涤一次后加入底物显色,10 min后加入终止液,然后在450 nm处测定样品及对照的吸光度值,并按照试剂盒说明书对样品血清值进行判断。

4.2 IFLRO算法的求解计算过程
IFLRO算法求解步骤如下。
步骤1:设定初始解、初始方向与步长。
步骤2:计算光线传播方向,并参照4.1 节计算光线传播位置。
步骤3:确定光线位置。确定与步骤2中所选vk+2对应的xk+2,将xk+2包含的坐标变量(m1,m2,…,mi)根据式(30)进行0-1判断。

步骤4:重复步骤2、3,直到满足终止迭代条件,并输出结果。终止迭代条件为:

式中:K1为迭代次数。
IFLRO算法流程如图2所示。

图2 IFLRO算法流程图Fig.2 Flowchart of IFLRO algorithm
4.3 动态聚合模型的求解步骤
步骤1:输入初始数据,包括风电场、光伏电站出力数据,电力系统的功率平衡约束,风电出力单元的运行约束,光伏出力单元的运行约束,弃风弃光率约束。
步骤2:输入主要参数,包括初始解、初始方向、初始步长、迭代条件。
步骤4:利用IFLRO 算法对VPP 动态聚合模型进行求解,得到寻优结果。
5 仿真分析
5.1 数据采集
本文根据新疆某地区的风电场和光伏电站以及全年负荷实测数据进行分析验证,该地区包含6 个风电场和3 个光伏电站。其中1 号风电场容量为100 MW,2 号风电场容量为50 MW,3 号风电场容量为150 MW,4 号风电场容量为200 MW,5 号风电场容量为200 MW,6 号风电场容量为100 MW,7—9号光伏电站容量均为20 MW。
5.2 参数设置
本文研究对象有6个风电场和3个光伏电站,因此该目标函数为9 维函数寻优。IFLRO 算法初始解和初始方向的设置虽不影响该算法的最优解,但步长的设置将直接影响该算法的求解速度及精度。本文设置初始解x0=(1,0,1,1,0,1,1,0,1),初始方向见附录C。考虑到算例对算法求解速度及精度的要求,本文将步长设置为0.1,最大迭代次数为500。
5.3 仿真结果及分析
5.3.1 元件停运概率对可再生能源出力的影响
为了对可再生能源出力不确定性进行定量描述,下文将以第一季度为例,利用序贯蒙特卡洛法分别将修正前、后单个风电场和光伏电站的出力曲线及可靠性指标进行对比。风电场和光伏电站4 个季度出力曲线修正前、后对比分别如附录D 图D1和图D2 所示。比较图D1 和图D2 不难发现,考虑元件故障率和修复率的出力模型和基本出力模型相比有着较大的出力变化。从图中可以看出,部分蓝色出力曲线并未被红色出力曲线覆盖,说明考虑了元件故障率与修复率之后,对其基本出力模型起到了一定的修正作用。附录D 表D1 和表D2 分别为风电场和光伏电站在修正前、后的可靠性指标。
分析可知:在是否考虑元件停运概率的2 种情况下,计算得到的风电场和光伏电站可靠性指标差异较为明显。并且在考虑元件停运概率的情况下,风电场和光伏电站的δLOLP、δLOLE、δEENS指标都有一定程度上升,以评估第一季度风电场可靠性为例,各指标分别提高了3.93%、16.22%、27.34%。说明此时风电场的停电概率、停电时间和供电缺额增大,机组出力的不确定性更加显著,其出力模型更具有普遍性。通过对比2种情况下的可靠性指标,说明元件停运概率对风电、光伏的出力模型起到了一定的修正作用,使其更具有普遍性,为后续计算VPP可靠性指标及VPP动态聚合模型的求解提供了更准确的参数。
5.3.2 不同方法对VPP动态聚合结果的影响
本文采用以下2 种评估方法对同一个VPP 的可靠性进行评估。方法1:分别计算VPP 内各风电场和光伏电站的可靠性指标,将所有场站可靠性指标累加作为VPP 的可靠性指标;方法2:在计算各风电场、光伏电站可靠性指标的基础上再分别对各场站的置信容量进行求解并求和,然后计算所有风电场和光伏电站总的置信容量所对应的常规机组的可靠性指标作为VPP 可靠性指标。以第一季度为例,计算结果如表1所示。

表1 不同评估方法下的VPP可靠性指标Table 1 VPP reliability indexes with different evaluation methods
从表1 可知,通过使用2 种评估方法对同一个VPP 的可靠性进行评估,发现用2 种方法计算得到的可靠性指标差异较大。与方法2 相比可以发现,若采用方法1 评估VPP 的可靠性,会使VPP 真实的电量不足时间概率、电量不足时间、电量不足期望值都被严重高估,会给决策人员提供错误的参考,容易造成资源浪费的问题。因此,考虑置信容量的可靠性评估方法为VPP 可靠性的评估提供了有力的参考,为电网提供了正确的指引,进而提高了资源利用率。
5.3.3 VPP动态聚合对可靠性指标的影响
本文利用IFLRO 算法分别求解所有风电场、光伏电站和动态聚合后VPP 的可靠性指标,计算结果如附录D 表D3 所示。由表可知,VPP 在聚合前、后δLOLP、δLOLE、δEENS指标都有一定程度的减小,说明在考虑弃风弃光率最低的条件下,并不是VPP 内风电场和光伏电站的数量越多越好,例如在第一季度,与聚合前相比,δLOLP、δLOLE、δEENS指标在聚合后分别降低了18.5%、8.09%、40.45%,充分说明此时VPP 的停电概率、停电时间以及供电缺额都有所下降,可靠性得到了提高。通过对比可知,VPP在动态聚合前,由于其供电可靠性不高,导致电网对其下达的发电计划较少,使得可再生能源的消纳量较低;而VPP在动态聚合后,大幅提高了其供电可靠性及供电能力,降低了可再生能源出力的不确定性对电力系统安全稳定运行造成的影响,在进一步提升上网电量的同时,提高了电网对可再生能源调度的积极性。
5.3.4 VPP动态聚合对容量置信度的影响
容量置信度可衡量VPP动态聚合结果比拟常规电厂的能力,即VPP 能够替代多少常规机组计入电力系统平衡,换言之,VPP能够在多大程度上提供一个可被电网信赖并积极调度的容量。本文分别对不同季度VPP聚合前、后的容量置信度进行计算,其结果如表2所示。

表2 不同季度的容量置信度Table 2 Capacity confidence in different quarters
分析表2 可知,在等可靠性的前提下,VPP 的容量置信度在每一季度聚合前、后都有所增加,此时VPP 的容量置信度基本处于10%~20%之间,相比聚合前增加了约3%~5%。说明在满足弃风弃光率最低的条件下,VPP 的动态聚合效应降低了风光出力的不确定性,提高了VPP的供电稳定性,使其比拟常规电厂的能力更强,有助于提高风光消纳能力。
5.3.5 VPP动态聚合对弃风弃光率的影响
本文对采用VPP 动态聚合模型聚合前、后的弃风弃光率进行计算,如表3所示。

表3 采用VPP动态聚合模型聚合前、后的弃风弃光率Table 3 Wind and solar abandonment rate with VPP dynamic aggregation model before and after aggregation
由表3 可知,VPP 在动态聚合之前的弃风弃光率高达45%,弃风弃光现象严重,但VPP 在动态聚合后的弃风弃光率约为35%。由此可知,动态聚合后的VPP,在提高风电、光伏利用率的同时降低了弃风弃光率。
5.3.6 不同算法对VPP动态聚合结果的影响
以第一季度为例,本文将采用FLRO、IFLRO、PSO 算法的动态聚合结果进行对比。参数设置如下:PSO 算法的初始解与FLRO、IFLRO 算法一致,粒子数为40,学习因子为2,惯性权重为0.8,最大迭代次数为500。图3给出了随着迭代次数的增加,不同算法的计算结果收敛的过程。

图3 不同算法下的δEENS的变化曲线Fig.3 Variation curve of δEENS with different algorithms
由图3 可知,随着迭代次数的增加,FLRO 算法的寻优结果明显发散,而PSO 算法和IFLRO 算法的寻优结果逐渐收敛且最终结果基本一致,由此说明IFLRO 算法在求解VPP 动态聚合模型时的有效性。本文选取了各季度迭代结果重复次数最高的组合,依次为:第一季度有1、3—7、9 号电站;第二季度有1—6、9号电站;第三季度有1—7、9号电站;第四季度有1、3—9号电站。
为体现IFLRO 算法的高效性,本文将IFLRO 和PSO 算法的计算时间进行对比,可得到PSO 算法的计算时间为47 905 s,IFLRO 算法的计算时间为35 829 s。由此可知,IFLRO 算法的计算时间明显小于PSO 算法,证明了该算法在求解VPP 动态聚合模型时的高效性,有助于运行人员及时调整运行计划,配合电网调度。由于该算例采用小时作为采样单位对每一季度进行计算,数据量大,并且每一种排列组合都要进行上千次的计算,故计算时间较长。
此外,本文还对IFLRO 算法的稳定性进行验证分析,同样将PSO算法与之对比。以第一季度为例,进行100次计算,其计算结果如图4所示。

图4 2种算法下的最优结果变化曲线Fig.4 Variation curve of optimal results under two algorithms
由图4 可知,在对本文模型的求解应用中,PSO算法稳定性表现欠佳,计算结果存在较大波动;而IFLRO算法计算所得的结果偏差控制在1.29%以内。若研究对算法稳定性要求较高的问题时,IFLRO 算法具有更明显的优势。
6 结论
本文针对风电、光伏出力的不确定性,提出了一种计及可再生能源可靠性的VPP 动态聚合方法,根据仿真结果得到如下结论。
1)在风电、光伏出力模型的基础上,利用元件的停运概率对可再生能源的出力模型进行修正,提高了出力模型的精度。
2)与现有VPP 可靠性指标计算方法相比,本文将置信容量引入对VPP可靠性指标的计算中。该方法可以将不同类型机组进行同质化处理,提高了可靠性指标的计算精度,为电网提供准确的参考。
3)相比静态聚合的VPP 模型,本文提出的VPP动态聚合模型充分考虑了外部环境因素及可再生能源自身潜力,深度挖掘出可靠性最佳的VPP 动态聚合方案,可在提高可再生能源消纳能力的同时,进一步提高VPP整体的灵活调控能力,减少资源浪费,为碳达峰、碳中和提供新思路。
4)为适应多维函数的寻优,本文提出了IFLRO算法,对发生反射与折射判断条件进行改进,从而提升了算法的寻优能力。在VPP动态聚合模型求解过程中,引入了可靠性指标来评价各算法的优劣。算例结果表明相比PSO 算法和FLRO 算法,采用所提IFLRO算法得到聚合结果的速度更快,稳定性更好。
但本文并未考虑火电机组和储能系统对VPP可靠性及经济性的影响,后续需对此进行深入的研究。
附录见本刊网络版(http://www.epae.cn)。
