基于D-FNN的盾构机协调优化控制
2022-07-20李记军
李记军
(无锡地铁建设有限责任公司,江苏 无锡 214021)
盾构机是一种常用于隧道施工的掘进机。近年来,随着我国隧道工程的发展,盾构机的应用越来越频繁,关于盾构机及其相关控制问题的研究越来越深入。但由于技术限制等,在盾构机掘进过程中的智能控制和优化方面还面临诸多难题,比如如何确保盾构机在高精度掘进的同时维持密封舱内土压平衡等。针对诸如此类的问题,相关专家进行了研究。杨悬[1]构建了盾构机刀盘、刀具三维实体模型并输入ANSYS软件,设计了盾构刀盘虚拟样机结构优化系统,改善了盾构机密封舱内的土压波动,一定程度上实现了盾构机的协调优化;李锟等[2]、来弘鹏等[3]采用多元线性回归和随机森林方法对土压平衡盾构施工区间的微风化灰岩地层段的主要掘进参数进行建模预测,实现了对土压平衡的有效控制,为实际盾构机施工操作提供了理论支持。上述方法虽取得了一定成果,但对盾构机土压平衡的控制精度还有待提高。动态模糊神经网络(dynamic fuzzy neural network,D-FNN)结合模糊控制系统与神经网络模型,可同时进行网络辨识和自适应参数调整,具有学习速度快、泛化能力强的优势,有利于提高盾构机土压平衡的控制精度。因此,本文基于D-FNN设计了盾构机协调优化控制模型。
1 基于D-FNN的盾构机协调优化控制模型构建
D-FNN网络结构分5层,具体如图1所示[4]。图中,x1,…,xr为模型输入;MFfm为输入f的第m个隶属函数;RN表示第N个模糊规则;Na表示第a个归一化节点;wu为第u个连接权值;y为模型输出。D-FNN网络具有学习速度快、泛化能力强的优势,可解决盾构机在掘进过程中土压平衡控制系统耦合程度高等问题[5-7]。因此,基于D-FNN网络构建盾构机协调优化控制模型,以平衡盾构机密封舱内的土压。
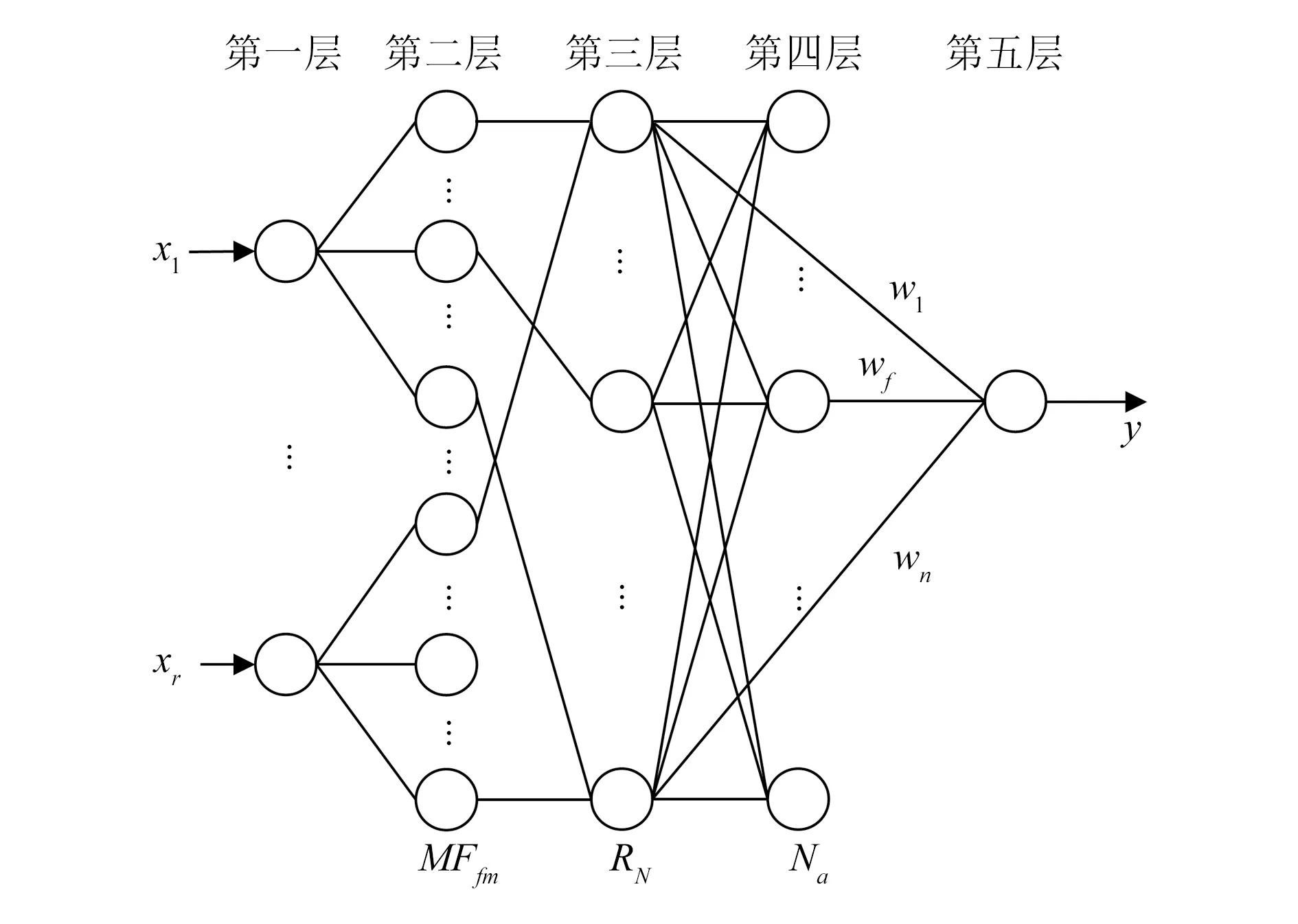
图1 D-FNN网络结构示意图
1.1 输入层神经元确定
根据盾构机掘进机理可知,螺旋机转速、盾构机当前推进速度、推力、刀盘扭矩与密封舱土压存在密切的非线性关系[8],因此以上述4个参数作为D-FNN模型的输入。此外,考虑到非线性开环控制对盾构机的协调优化控制效果较差,将以D-FNN输出的实测密封舱土压和土压设定值的误差作为模型的输入之一,构成可自动调节参数的闭环控制,以提高控制效果。
1.2 输出层神经元确定
本文盾构机密封舱土压平衡协调优化控制的目的是在盾构机推进与排土结合控制模式下,实现进土量与出土量的动态平衡,以保证密封舱土压值与设定值始终保持一致。因此,本文以螺旋输送机转速与盾构机下一时刻的推进速度为D-FNN模型的输出。
1.3 激活函数与隶属函数确定
激活函数的选择不仅要考虑其是否具备良好的全局映射能力,还需考虑其是否具备局部细化的能力。由于高斯函数具有各向同性特点,同时具备良好的全局映射能力和局部细化能力[9],因此本文选用高斯函数作为D-FNN模型的激活函数。隶属函数反映了观测数据的某种隶属度,主要有高斯函数和三角函数两类[10]。D-FNN模型是将知识语言规则转化为数学模型来控制行为特征,而高斯函数可对数学模型表达不确定性进行决断,因此本文选用高斯函数作为D-FNN模型的隶属函数。
1.4 模糊规则数量确定
理论上,D-FNN模型的模糊规则数量越多,模型可容纳的观测数据越多,模型控制效果也越好。但考虑到过多的观测数据容易导致模型参数出现过拟合,因此有必要对模糊规则进行筛选,剔除对模型贡献较小的模糊规则,以提高模型的辨识效率。本文选用常用于修剪模糊规则数量的误差下降率法对模糊规则进行筛选[11-12]。
1.5 模型结构确定
基于上述设定,本文设计的基于D-FNN网络的盾构机协调优化控制模型如图2所示。
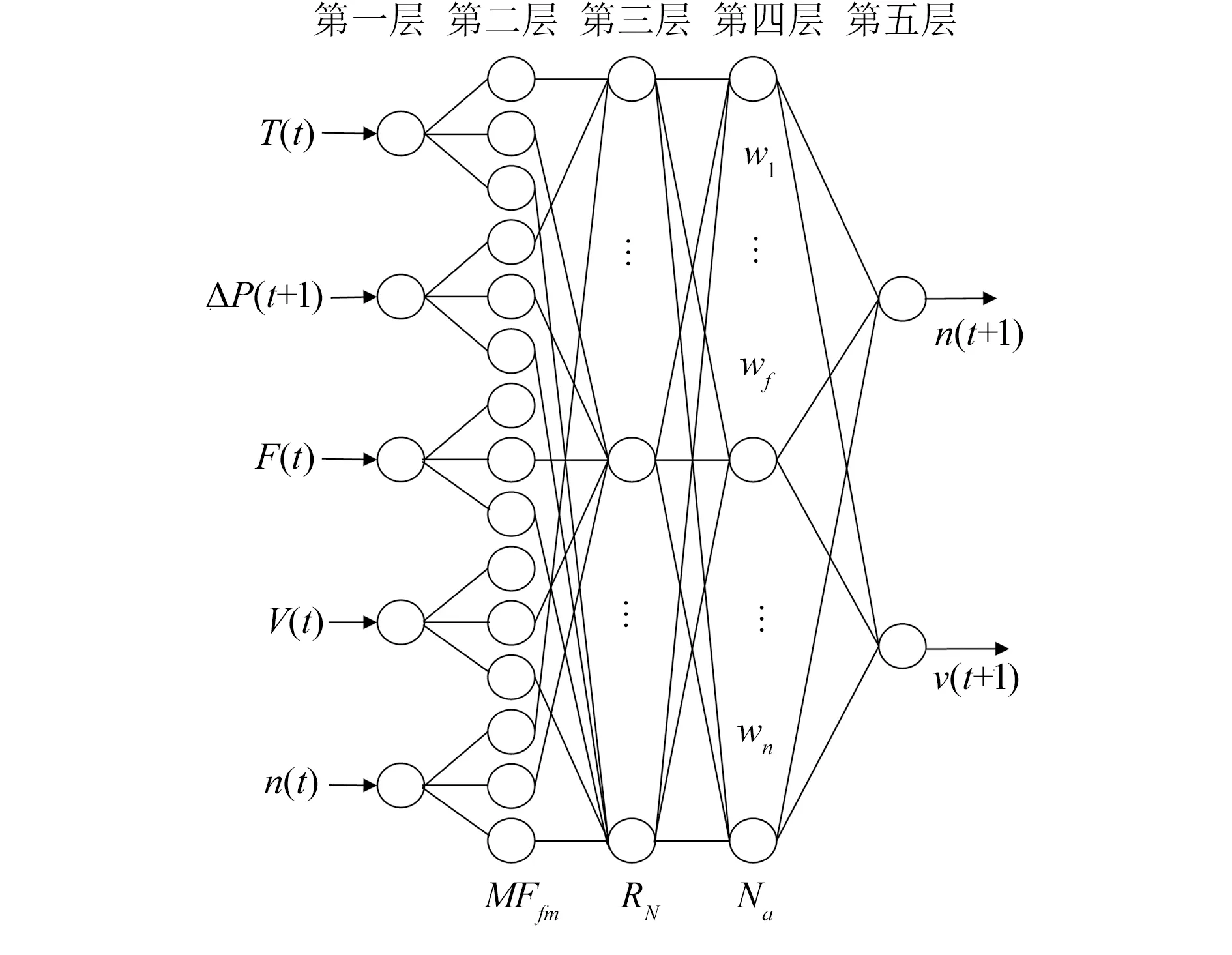
图2 基于D-FNN的盾构机优化控制模型结构
图中,T(t)为刀盘转矩;F(t)为推力;V(t)为盾构机推进速度;n(t)为螺旋输送机转速;ΔP(t+1)=P(t+1)-P,为期望土压与实测土压的误差反馈量,其中P为期望土压,P(t+1)为实测土压;n(t+1)、v(t+1)分别为D-FNN输出的螺旋输送机转速和盾构机下一时刻的推进速度,其计算方式如式(1)[13-14]。
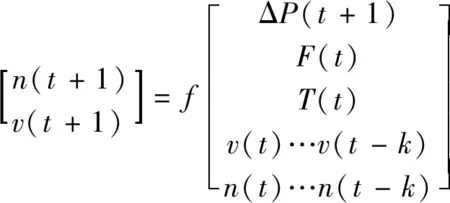
(1)
式中:v(t)…v(t-k)表示盾构机推进速度序列;n(t)…n(t-k)表示螺旋输送机转速序列。
2 模型训练
对构建的基于D-FNN的盾构机优化控制模型进行训练,首先设置盾构机螺旋机转速、推进速度、推力等初始数据并产生一条模糊规则,然后判断输入的观测数据Xi与高斯单元中心最小距离dmin和可容纳所有观测数据范围的有效半径kd的大小。如dmin>kd,则增加模糊规则数量,反之则减少模糊规则数量。最后,产生新的高斯单元,获取最佳网络模型。模型训练流程如图3所示[15]。图中,ek为预先设定的误差阈值,ηv为误差下降率,kw为预先设定的误差下降率阈值。
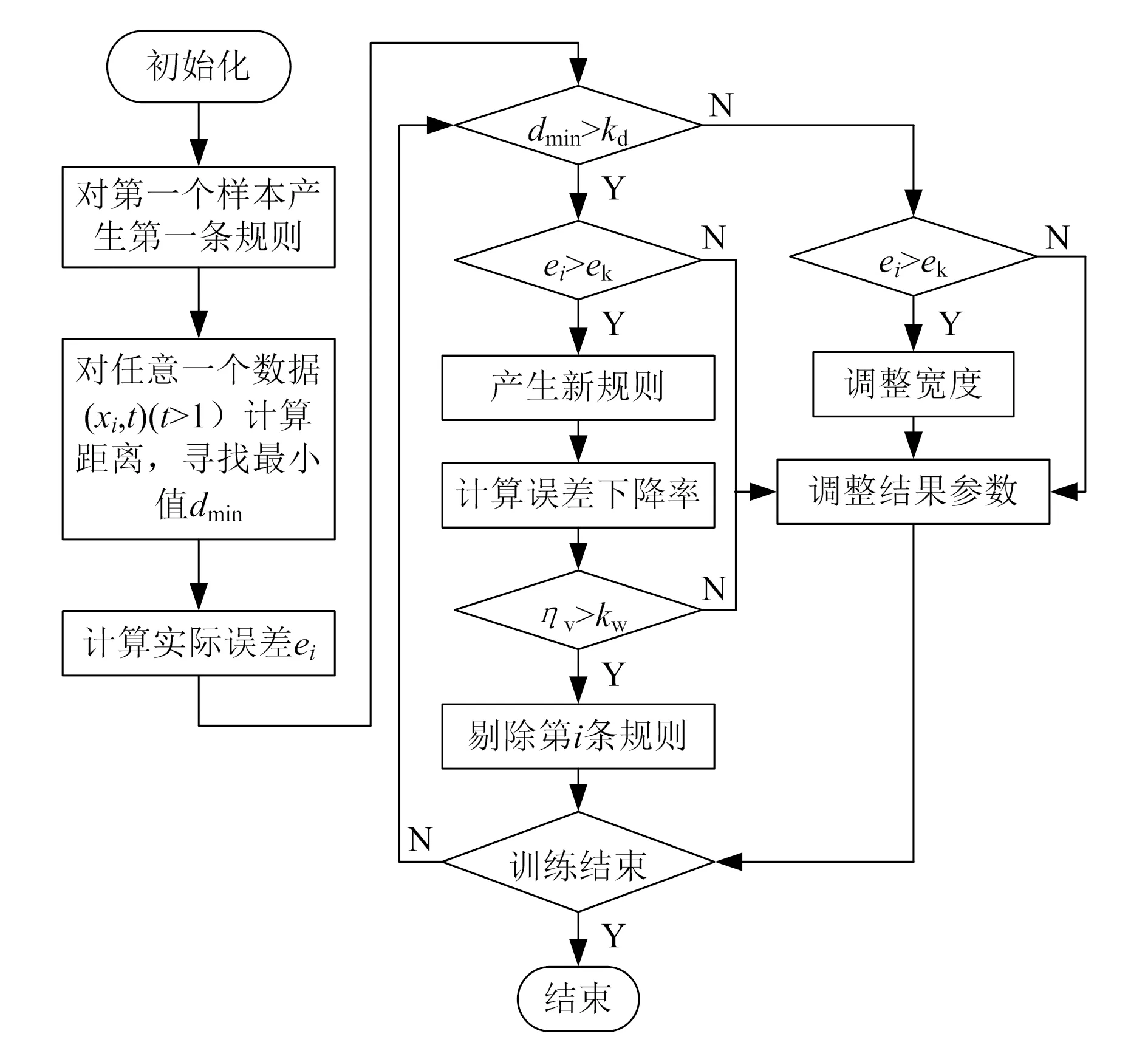
图3 基于D-FNN盾构机控制模型训练流程图
3 仿真实验
3.1 数据来源及模型参数设置
本次实验数据来自盾构机内置传感器检测的800组盾构机掘进施工数据,并以3∶1的比例随机将采集数据分为模型训练集(600组)和测试集(200组)。模型参数具体设置如下:学习率为0.002,惯性系数为0.05,辨识后模糊规则数为13,迭代次数为1 000。
3.2 结果与分析
3.2.1模型验证
为验证提出的模型对盾构机协调优化控制的效果,首先采用训练集对模型进行训练;然后利用测试集对训练完成的模型进行仿真,得到模型的输出;最后将模型输出与实际现场盾构机施工数据进行对比,得到如图4~图6所示的结果。图4为模型优化后螺旋输送机转速与实际速度对比;图5为模型优化后盾构机推进速度与实际速度对比;图6为模型优化后密封舱土压波动情况与实际土压波动情况对比。
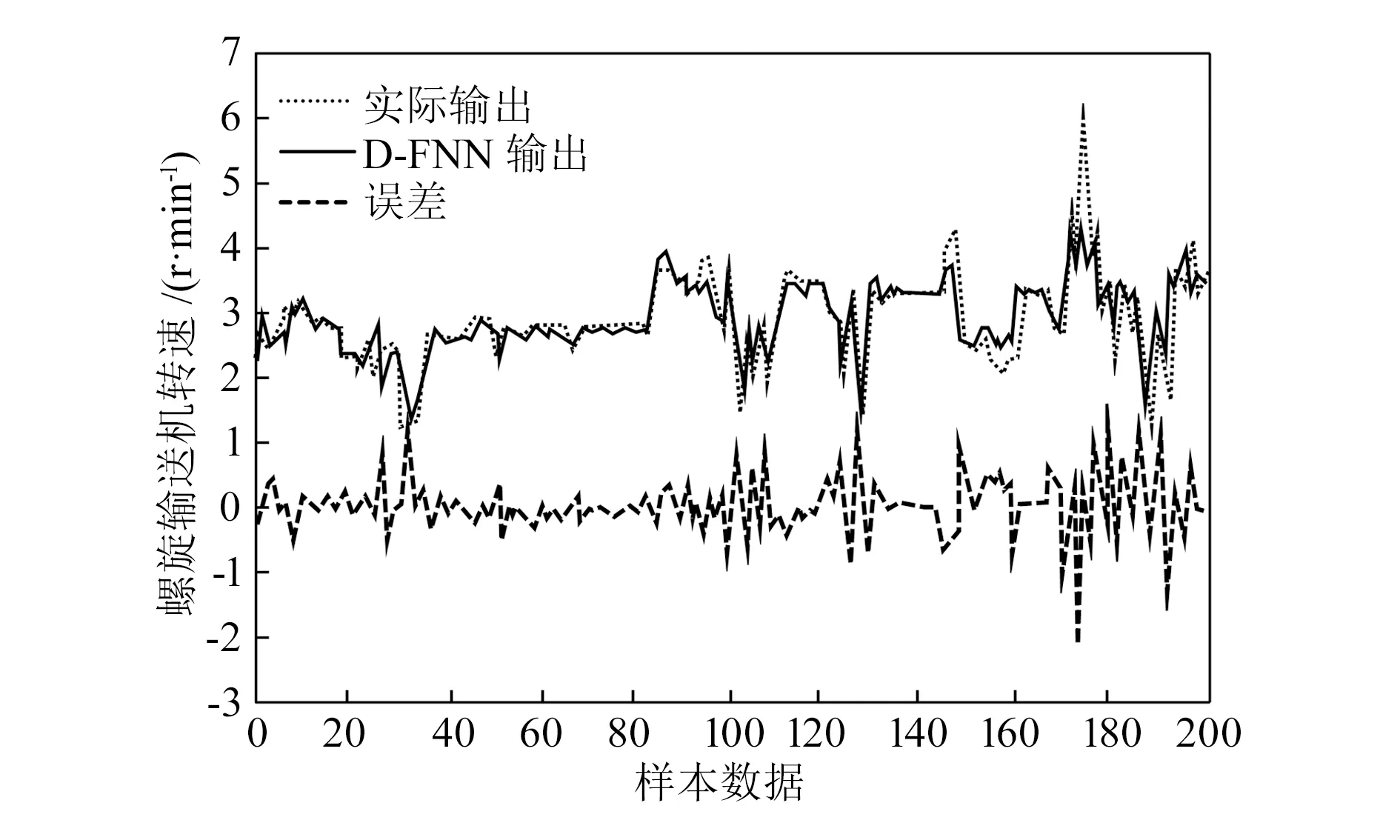
图4 螺旋输送机转速对比
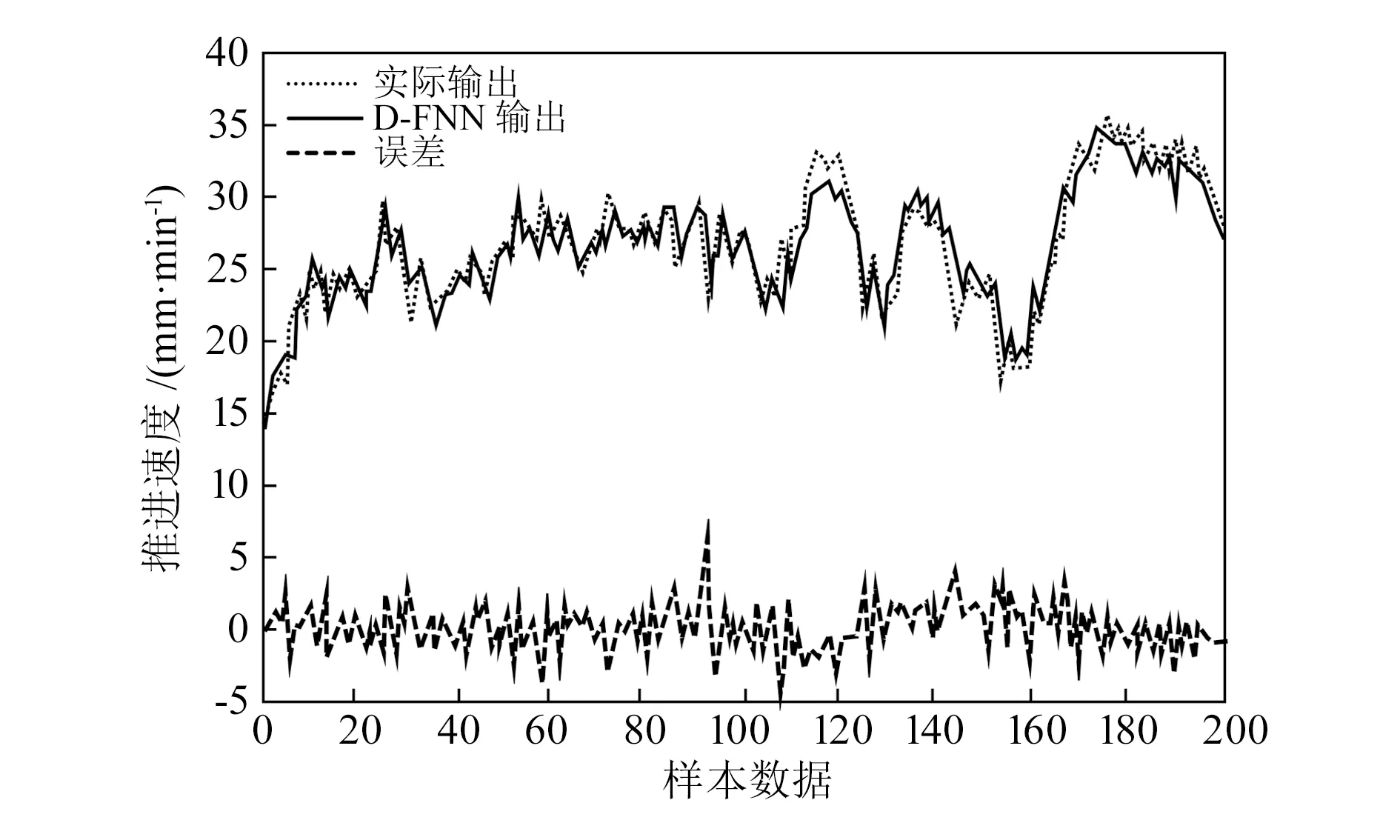
图5 盾构机推进速度对比
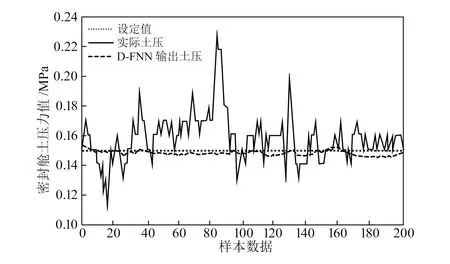
图6 密封舱土压波动情况对比
由图4、图5可知,采用D-FNN网络模型优化后的螺旋输送机转速和盾构机推进速度与实际值变化趋势相符,均方误差分别为0.189和2.546,在误差允许范围内。
由图6可知,盾构机掘进过程中,密封舱土压始终处于波动状态,实际值平均波动误差为8.46%,而通过D-FNN模型优化后,密封舱土压的波动明显下降,与设定值0.15 MPa接近,平均波动误差为1.45%。由此说明,本文提出的D-FNN模型可根据实际施工环境优化盾构机螺旋输送机转速和盾构机下一时刻的推进速度,改善密封舱土压,实现盾构机密封舱土压平衡。
3.2.2模型对比
为进一步验证本文所提出模型的优越性,基于相同的盾构机掘进数据,分别采用本文模型和BPNN(BP网络)模型对盾构机进行优化控制,得到两种模型的土压控制效果,如图7所示。由图可知,相较于BPNN模型,本文所提模型控制下的密封舱土压波动情况与设定值更接近,说明所提模型的控制效果更好,优于BPNN模型。
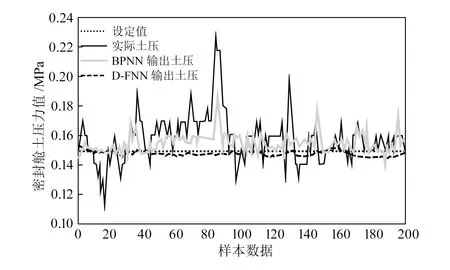
图7 不同模型控制下密封舱土压波动情况
为定量分析D-FNN模型和BPNN模型对密封舱土压的控制误差,计算得到两种模型对螺旋输送机转速、盾构机下一时刻推进速度的均方差(MSE)以及土压波动相对误差,见表1。由表可知,BPNN模型控制下的螺旋输送机转速与实际值的均方误差为0.509,盾构机下一时刻推进速度与实际值的均方误差为3.428,土压波动相对误差为4.53%,均大于D-FNN控制下的均方误差和相对误差。由此说明,所提D-FNN模型对盾构机的协调优化控制优于BPNN模型,可最大程度降低盾构机掘进过程中密封舱土压波动,具有一定的实用价值。
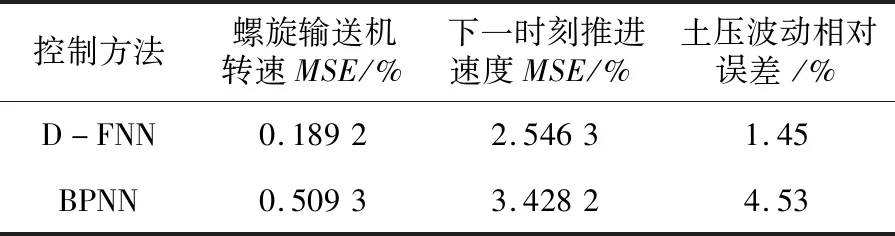
表1 不同模型控制误差分析
4 结束语
本文所提的基于D-FNN网络的盾构机协调优化控制方法,可根据实际施工环境优化盾构机螺旋输送机转速和盾构机下一时刻的推进速度,改善盾构机掘进过程中密封舱的土压,使土压平均波动误差仅为1.45%。相较于传统BPNN优化控制方法,本文提出的方法控制效果更好,具有一定的实用价值。但由于条件限制,本文的研究仍存在一些不足之处,主要是提出方法的普适性不足。我国地域辽阔,环境复杂多变,盾构机施工中遇到的困难各种各样,而本文没有对提出方法在不同施工环境下的适用性进行研究。因此,下一步将选取更多具有代表性盾构机施工数据,进一步完善所提方法,以提高方法的普适性。
