成组序贯设计中经典期中分析方法的比较

张晓岚, 蔡淳淳, 陈晔

(1. 长沙理工大学数学与统计学院, 湖南长沙,410114;2. 湖南文理学院数理学院, 湖南常德,415000)

在临床研究中有一种科学的方法允许在收集完最终样本前分析数据并提前停止试验, 这个方法就是成组序贯设计。成组序贯设计相较于传统的固定样本量设计的优点显而易见, 它可以缩短试验时间,减小样本量。

1977 年,Pocock[1]提出了等间距成组序贯设计。成组序贯设计会进行期中分析, 即根据事先制定的分析计划, 对累计数据进行分析, 由于该设计需要对累计数据进行检验, 故需控制各阶段的一类错误。Pocock 是将整体第一类错误均匀分配到各阶段。O′Brien 等[2]提出的期中分析方法在试验前半段边界较为保守, 即在试验进行到后半段之前停止试验的概率非常低。Lan KKG 等[3-4]引入了α消耗函数的概念,它是[0,1]映射到[0,α]的连续、非递减的函数, 其中α是第一类错误。成组序贯设计中的第一类错误控制一直是一个热点话题, 郭静等[5]通过计算最大样本量结合实例说明了几种期中分析方法的应用。Li 等[6]针对临床试验中成组序贯设计中的次要终点的第一类错误控制策略进行了讨论。刘伟杰等[7]则是基于O′Brien-Fleming 方法讨论比较了随机缩减法中条件功效和不同先验分布下的预测功效两类指标的优劣。本文比较了几类经典的期中分析方法的临界值、期望样本量等参数, 并据此总结了各类方法特点。

1 方法

因为ti,i=1,…,K在试验开始前是未知的, 此时将式(1)转换为

1.1 Pocock 临界常量

1977 年,Pocock 提出在成组序贯设计中采用相同的临界常量ci进行多次重复显著性检验, 即c1=…=cK=c。为了控制试验的整体第一类错误, 临界常量c需满足公式(2),(2)式变形可得

根据式(3)并利用布朗运动的性质结合多元正态分布函数即可确定临界常量c。

1.2 O′Brien-Fleming 临界常量

1979 年,O′Brien 和Fleming 建议采用递增的名义检验水准法则, 在试验进行过程中逐渐放宽检验的阈值, 减小相应临界常量的取值。

根据式(4)即可确定m, 进而确定c1, …,cK。

到目前为止, 上述两种成组序贯设计方法构造出的临界常量是离散的, 具有较大的局限性。在实践中这可能会导致一些问题, 比如试验小组可能会在试验过程中的某个时刻改变数据分析的频率, 或者招募患者的速度慢于预期, 可能会导致试验终止延期, 从而增加期中分析的次数等情况, 因此, 引入了一种由Lan KKG 和Demets[3-4]提出的更加灵活的方法—α消耗函数法。

1.3 α 消耗函数法

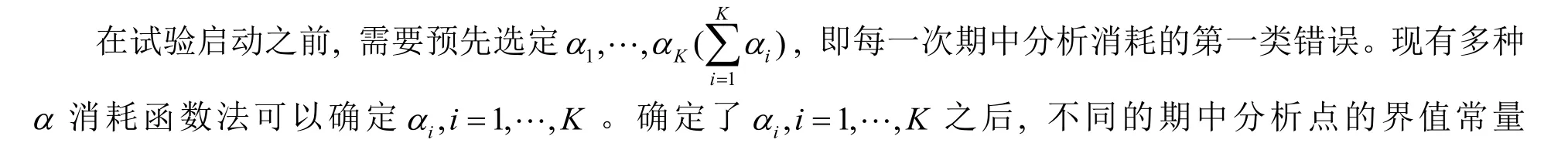
2 结果与分析

在成组序贯设计中, 确定了临界常量之后, 可以通过控制其效能确定其最大的信息量, 即

如表1 所示, 是根据7 种期中分析方法计算的临界值、样本量以及通过1×105次模拟获得的每次期中分析的经验第一类错误。比较这7 种期中分析方法可知, 基于α消耗函数的O′Brien-Fleming 方法和Pocock 方法(α1*(s)和α2*(s))计算所得的各类参数如临界值、样本量以及模拟所得经验第一类错误都和O′Brien-Fleming 方法和Pocock 方法计算所得非常类似, 但也有些许不同, 相较于O′Brien-Fleming 方法,α消耗函数的O′Brien-Fleming 方法在试验前期更为保守;α消耗函数Pocock 方法则和Pocock 方法非常类似, 临界值、样本量和模拟第一类错误都非常接近;α消耗函数的另外3 种方法(α3*(s)、α4*(s)和α5*(s))的期望样本量、经验整体第一类错误和经验统计效能则是介于Pocock 方法和O′Brien-Fleming 之间。

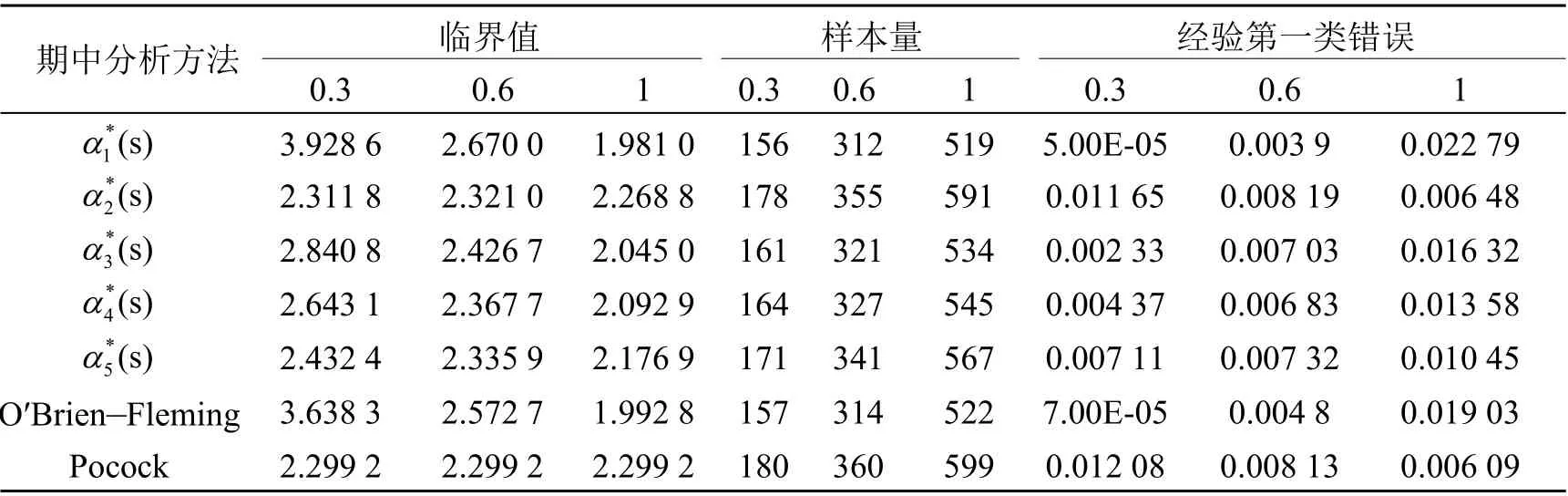
表1 几类期中分析方法的临界值、样本量和经验第一类错误

多数文献通过最小化期望样本量来优化成组序贯设计[10], 因此通过期望样本量来比较这几种期中分析方法, 通过十万次模拟试验, 计算出这几种期中分析方法的期望样本量、经验整体第一类错误、经验效能以及固定样本量设计所需的样本量, 如表2 所示。

由表2 可知, 通过模拟获得的这7 类期中分析方法的第一类错误和效能是比较准确的, 都是非常接近事先给定的α和1-β, 说明了这几种期中分析方法的有效性和样本量的准确性。几类期中分析方法的期望样本量是明显小于固定设计的样本量的, 因为成组序贯设计存在着提前停止试验的可能。将几类期中分析方法进行比较,O′Brien-Fleming 临界值和基于α消耗函数的O′Brien-Fleming 方法(α1*(s))所需样本量是最大的,Pocock临界值和基于α消耗函数的Pocock 方法(α2*(s))所需样本量是最小的, 另外几种基于α消耗函数的方法计算所得期望样本量是介于两者之间的。

表2 7 种期中分析方法的期望样本量、经验整体第一类错误和经验效能

3 结论

由前文的模拟结果可知, 在具体的临床试验中, 可以根据实际情况出发选择合适的方法来确定临界值。从治疗效果的角度来看, 当需要满足在试验早期显示出极佳的治疗效果才可以停止试验的要求时,建议选择O′Brien-Fleming 方法; 当希望试验早期显示出在一定程度上有效的治疗效果就停止试验时,建议选择Pocock 方法; 在没有具体的实际情况约束下, 并倾向于使第一类错误分配的较为均匀时, 可以采取α消耗函数法中的α3*(s)、α4*(s)和α5*(s)来确定第一类错误的分配进而确定临界值。

由表1、2 可知,O′Brien-Fleming 方法的最大样本量小于Pocock 方法的最大样本量, 然而,O′Brien-Fleming 方法的期望样本量大于Pocock 方法的期望样本量, 这也说明了O′Brien-Fleming 方法在试验后期拒绝原假设的概率更大些, 而Pocock 方法相对来说第一类错误分配得更为均匀些。基于α3*(s)、α4*(s)和α5*(s)确定的最大样本量和期望样本量均是介于O′Brien-Fleming 方法和Pocock 方法之间, 综合来看,采取α3*(s)、α4*(s)和α5*(s)是更为严谨保守的。另外, 本文是基于Lan KKG 和Demets 提出的α消耗函数法来确定每一次期中分析时消耗的第一类错误αi,i= 1, …,K,在实际应用中, 试验的设计人员也完全可以按照实际情况自行控制每一次期中分析时消耗的第一类错误, 再根据式(5)、(6)确定临界值,α消耗函数法是分配整体第一类错误的方法, 但也可以不局限于某种分配方法来确定每一次期中分析的第一类错误, 也可以人为的根据试验要求直接设定每一次期中分析分配的第一类错误, 并根据式(5)和式(6)来确定每次期中分析时的临界常量。