不同路况下履带车辆轮胎的动力学特性仿真分析
2022-07-20张文海郑水利
张文海,郑水利
(重庆交通大学 机电与车辆工程学院,重庆 400074)
车辆在不同路况下的行驶试验是轮胎和悬架部件设计验证的关键[1]。轮胎在驶过凹凸不平的路面时变形很大,在极端情况下轮胎与凹凸坑的碰撞是否会导致轮胎损坏和漏气是轮胎设计人员关注的问题。为了评价轮胎的安全性,通常需要进行轮胎在不同路况下的行驶试验。但是对于一些恶劣的工况,由于试验成本高以及需要考虑不同类型的轮胎和不同的行驶工况,车辆试验并不容易进行。因此,开发一种有效的有限元模拟方法来预测不同路况下轮胎的碰撞性能具有重要意义。
基于有限元方法的轮胎动态仿真的关键问题是建立可靠的轮胎有限元模型[2]。一些研究人员致力于开发简化的轮胎模型,减少了轮胎材料数量,显著放大了网格尺寸[3-4]。简化的轮胎模型可以成功地用于轮胎力学分析,然而由于简化,轮胎的结构和材料特性没有得到真实的表达,因此无法为轮胎设计者提供足够的参考信息。近年来,随着有限元分析软件的发展和数值算法的进步,轮胎有限元建模和动态特性分析已经得到了大量研究[5-6],通过细致的几何结构和材料定义来分析高度复杂的非线性轮胎变得更加有效[7-8]。Y.L.ZHANG等[9]研究了车辆通过坑洞障碍物路况的特性,采用隐式与显式算法相结合的方法缩短仿真中的运行时间。
本研究提出一种研究履带车辆轮胎在不同路况下的动力学特性的仿真方法。首先建立轮胎精细有限元模型,然后在充分考虑轮胎的几何非线性、材料非线性和接触非线性的基础上模拟轮胎在垂直负荷作用下与路面的接触过程,分析轮胎驶过不同路况时的力学特性和变形。
1 轮胎模型的建立
1.1 三维模型
通过CAD制图软件对轮胎截面进行二维建模,然后将二维图形导入Abaqus软件中转化为三维图形[10],如图1所示。

图1 履带车辆轮胎三维模型
由于在进行有限元分析时考虑轮胎工作时存在的几何非线性、材料非线性及接触非线性会导致计算过程复杂、耗时长和难以收敛的后果,因此在合理的情况下可以对轮胎进行简化,以保证收敛和节约时间。本研究的侧重点是轮胎胎面与地面的接触应力分析,则可省去轮毂建模,采用Abaqus软件的刚体约束功能,把轮胎内表面与轮胎中心点(参考点)做刚体约束,视为一体。
1.2 网格划分与单元选择
在轮胎非线性有限元分析中网格划分是一个难点,仿真模拟结果的收敛性和计算精度等都受网格划分的影响。本研究轮胎模型通过简化可得到质量较好的网格。橡胶是一种典型的不可压缩材料,因此使用杂交单元,其主要用于不可压缩材料或者近似不可压缩材料,设置轮胎单元为C3D8RH,即为线性减缩积分杂交单元。
1.3 材料定义
轮胎的材料属于橡胶材料,常用的描述橡胶材料力学性能的方法有现象学方法和基于热力学统计理论的方法[11]。比较成熟的橡胶材料的本构模型主要有多项式模型和Ogden模型[12],本研究采用多项式本构模型。多项式模型的应变能函数可以表示为
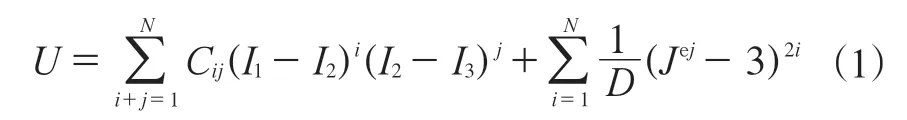
式中:U为应变能;N为多项式的阶数;Cij为描述材料剪切特性的参数;I1和I2表示材料的第一和第二应变不变量;D为表示材料压缩性的参数,若材料完全不可压缩,则D为0;J为弹性体积比。
如果多项式的阶数为1,即为Mooney-Rivlin材料模型,其应变能密度公式为
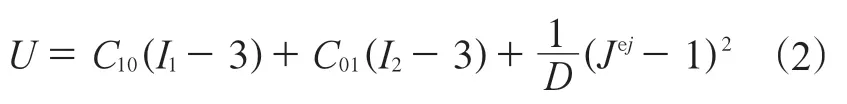
式(2)中C01=0时,则称为Neo-Hookean材料模型。本研究采用Neo-Hookean模型,轮胎橡胶材料的特性参数为:C10.5 GPa,D0.04 GPa,密度 1.1 Mg·m-3。
1.4 轮胎-地面接触模型
本工作采用精度高、适用性广的直接约束法描述接触问题。切向接触条件常使用库伦摩擦模型描述,该模型用摩擦因数来表征两个表面之间的摩擦特性,法向接触采用硬接触,摩擦因数为0.5,路面采用离散刚体,把路面视为不变形的刚体,采用离散刚体划分网格可以减少穿透。轮胎-地面接触模型如图2所示。

图2 轮胎-地面接触模型
2 不同路况下轮胎力学特性分析
实际上轮胎不只是在水平路面上行驶,而是在复杂的环境中工作,因此研究轮胎在不同路况下的力学特性和形变状态非常重要。
2.1 水平路况
在轮胎的动力学分析中,常常选用显式算法分析瞬态工况。相对于隐式算法,显式算法在每一个时间增量步的计算上耗用的计算资源和时间成本较低。本研究为瞬态工况分析,采用显式算法分析轮胎与地面间的滚动接触问题,以缩短计算时间。
轮胎-水平道路模型如图3所示。

图3 轮胎-水平道路模型
设置轮胎在水平道路原地启动,以20 km·h-1的速度匀速在水平道路上滚动一圈。在轮胎-地面接触模型的基础上,给轮胎参考点施加一个沿路面向前滚动的位移约束,设置时长为0.423 6 s,释放模型X方向的约束(X方向为前进方向),道路完全固定。总时长为0.573 6 s,包括垂直负荷加载阶段(0.100 s)、垂直负荷加载稳定阶段(0.050 s)和轮胎滚动阶段。水平路况轮胎切向力和法向力随时间的变化如图4所示。
由图4可以看出,轮胎在启动瞬间法向力急剧减小,但时间很短,之后马上恢复到40 000 N左右,随后又增大。由此可见,法向力随行驶时间呈现震荡,且幅度慢慢减小,最后趋向平稳。轮胎切向力与法向力的变化趋势基本一致,但幅度变化较为平缓。
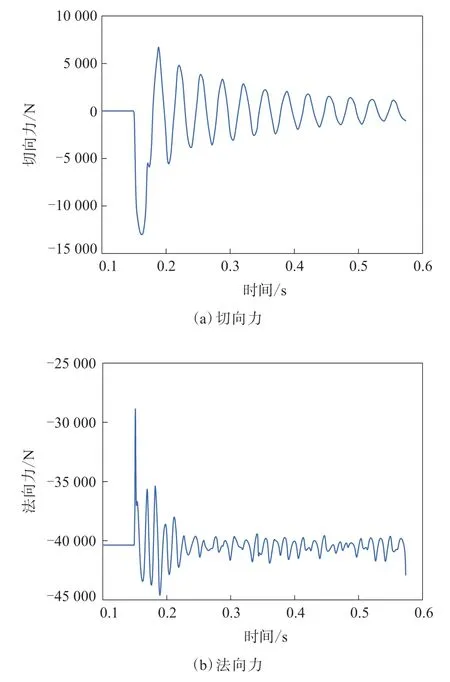
图4 水平路况轮胎切向力和法向力随时间的变化
2.2 带坡度路况
现实中更多的是具有坡度的道路,因此分析轮胎在带坡度道路上行驶的力学特性很有必要。本研究设计的道路坡度分别为5°和10°,轮胎-带坡度道路模型如图5所示。
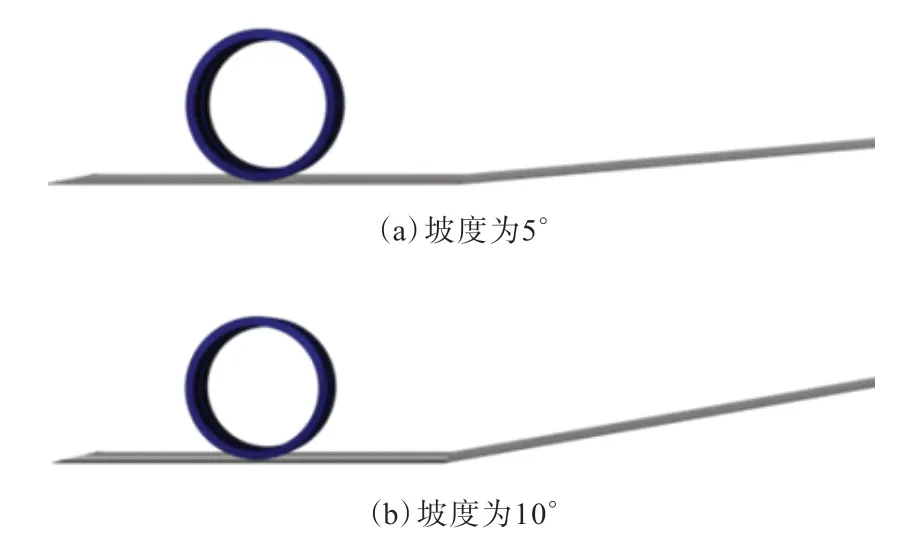
图5 轮胎-带坡度道路模型
设置轮胎在水平道路启动,待行驶一段距离后驶上坡道,总时长为0.785 4 s,包括垂直负荷加载阶段(0.100 s)、垂直负荷加载稳定阶段(0.050 s)、水平道路行驶阶段和坡度道路行驶阶段。速度为20 km·h-1,垂直负荷为40 000 N,摩擦因数为0.5。带坡度路况轮胎切向力和法向力随时间的变化分别如图6和7所示。
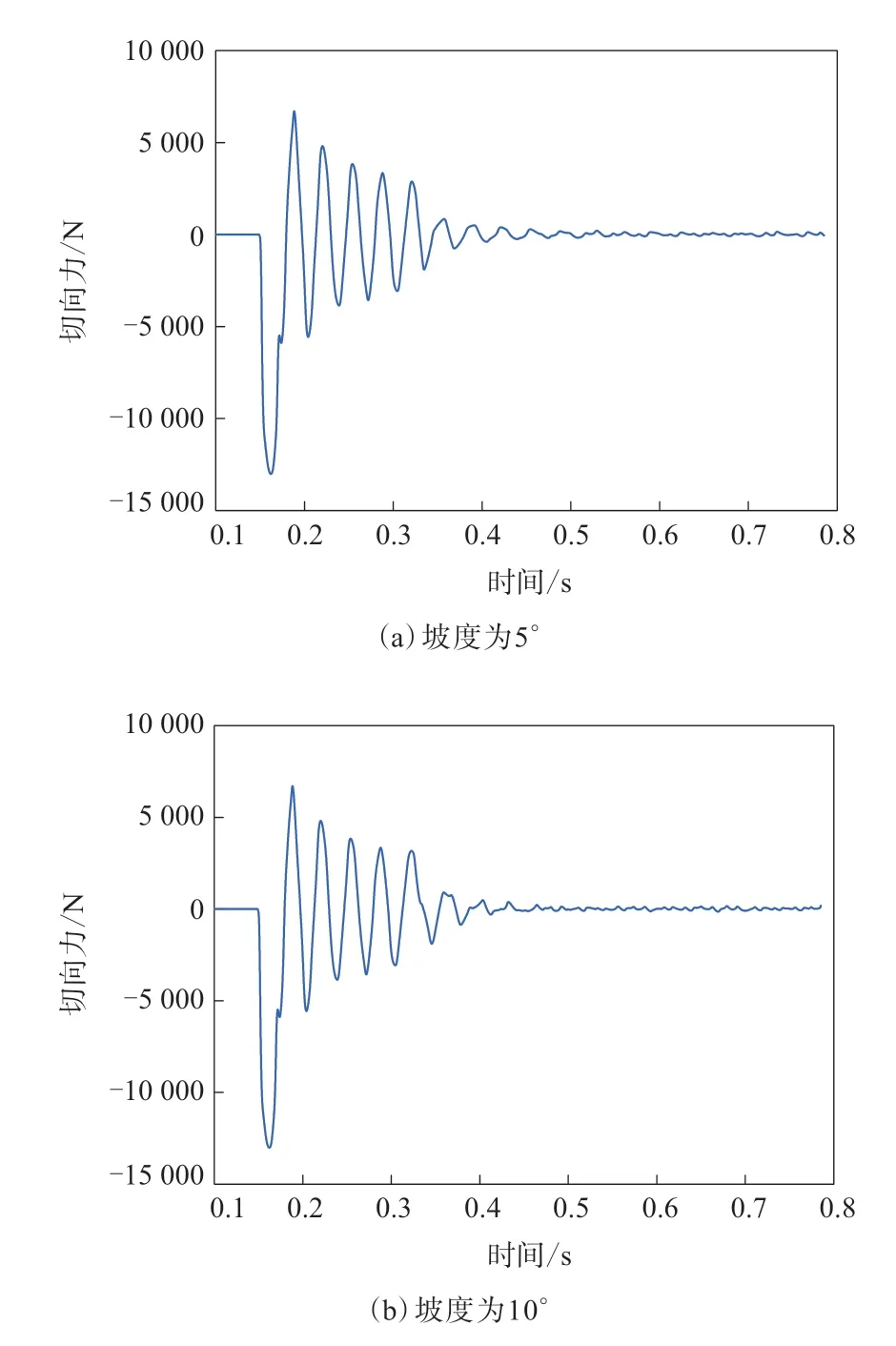
图6 带坡度路况轮胎切向力随时间的变化
分析轮胎的接地应力分布有助于研究轮胎与地面的作用原理,本工作重点关注轮胎在水平道路滚动结束后刚开始上坡碰到坡道时的力学特性。轮胎碰到坡道时的接触应力分布如图8所示。
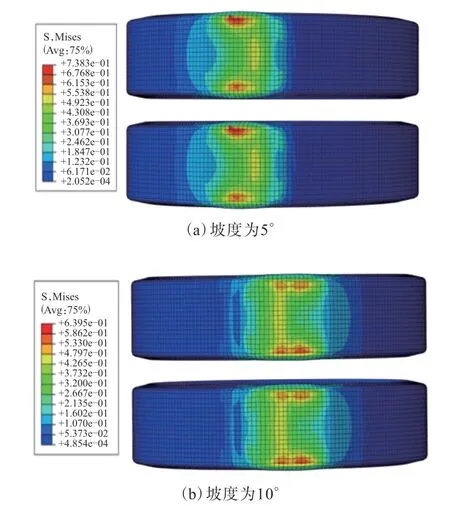
图8 轮胎碰到坡道时的接触应力分布
在0.330 s前,轮胎与水平滚动一致,受力呈现震荡,缓慢趋于平衡。在0.332 s时,轮胎碰到坡道产生变形。从图6可以看出,切向力在触碰到坡道的瞬间突然下降,且坡度越大下降越快,然后切向力迅速震荡趋于平衡。而法向力与切向力相反,从图7可以看出,轮胎触碰到坡道时法向力突然增大,且坡度越大增大越多,上坡后也呈现缓慢震荡趋于平稳。
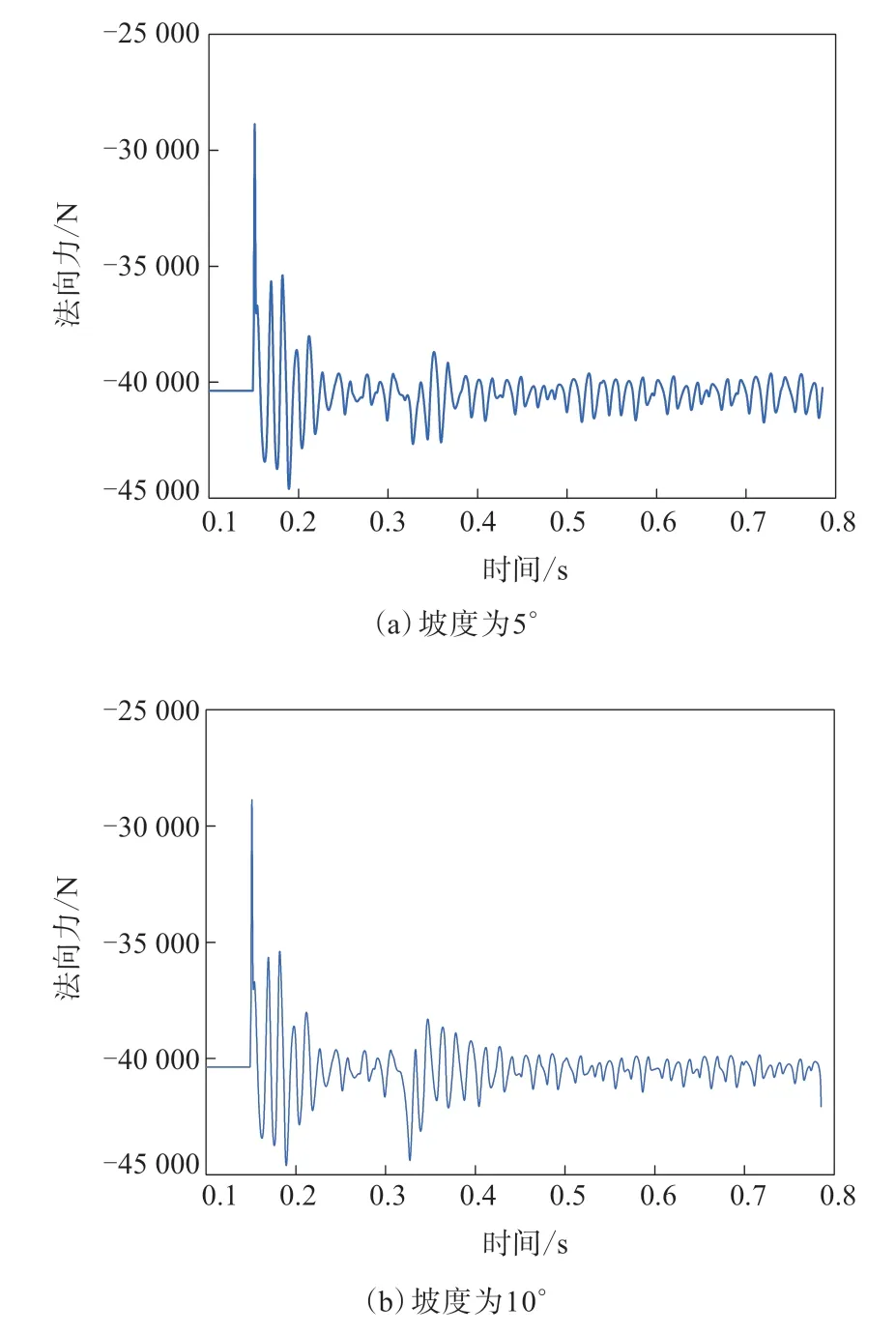
图7 带坡度路况轮胎法向力随时间的变化
从图8可以看出,轮胎接触面的高应力区都向前进方向移动,但是最大应力还是在轮胎边缘。
2.3 半正弦路况
在现实环境中经常遇到上坡然后下坡或者一些呈现幅度变化的道路,因此本工作采用半正弦道路模拟这种情况,半正弦道路模型如图9所示。
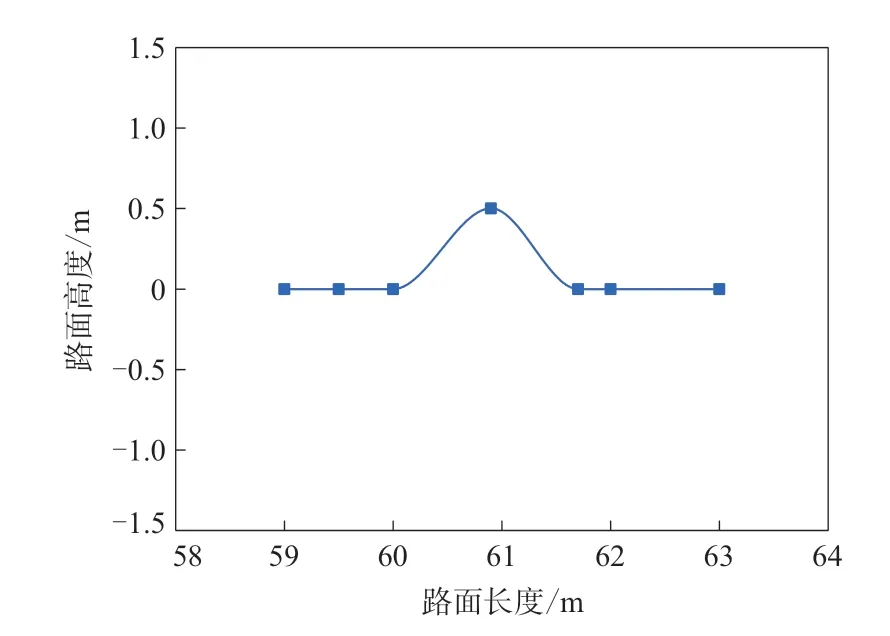
图9 半正弦道路模型
将道路模型设置为半正弦模型,与前面研究的条件相同,轮胎在水平道路起步,轮胎-半正弦道路模型如图10所示。在水平道路与半正弦坡度处采用圆弧过渡可以减小对轮胎的冲击,更为接近实际情况。

图10 轮胎-半正弦道路模型
在通过半正弦坡道时,考虑坡度较大,为了保证轮胎上坡时不打滑,将摩擦因数设置为0.8。总时长为0.785 5 s,包括垂直负荷加载阶段(0.100 s)、垂直负荷加载稳定阶段(0.050 s)、水平道路行驶阶段(0.292 2 s)和半正弦道路行驶阶段。半正弦路况轮胎切向力和法向力随时间的变化如图11所示。
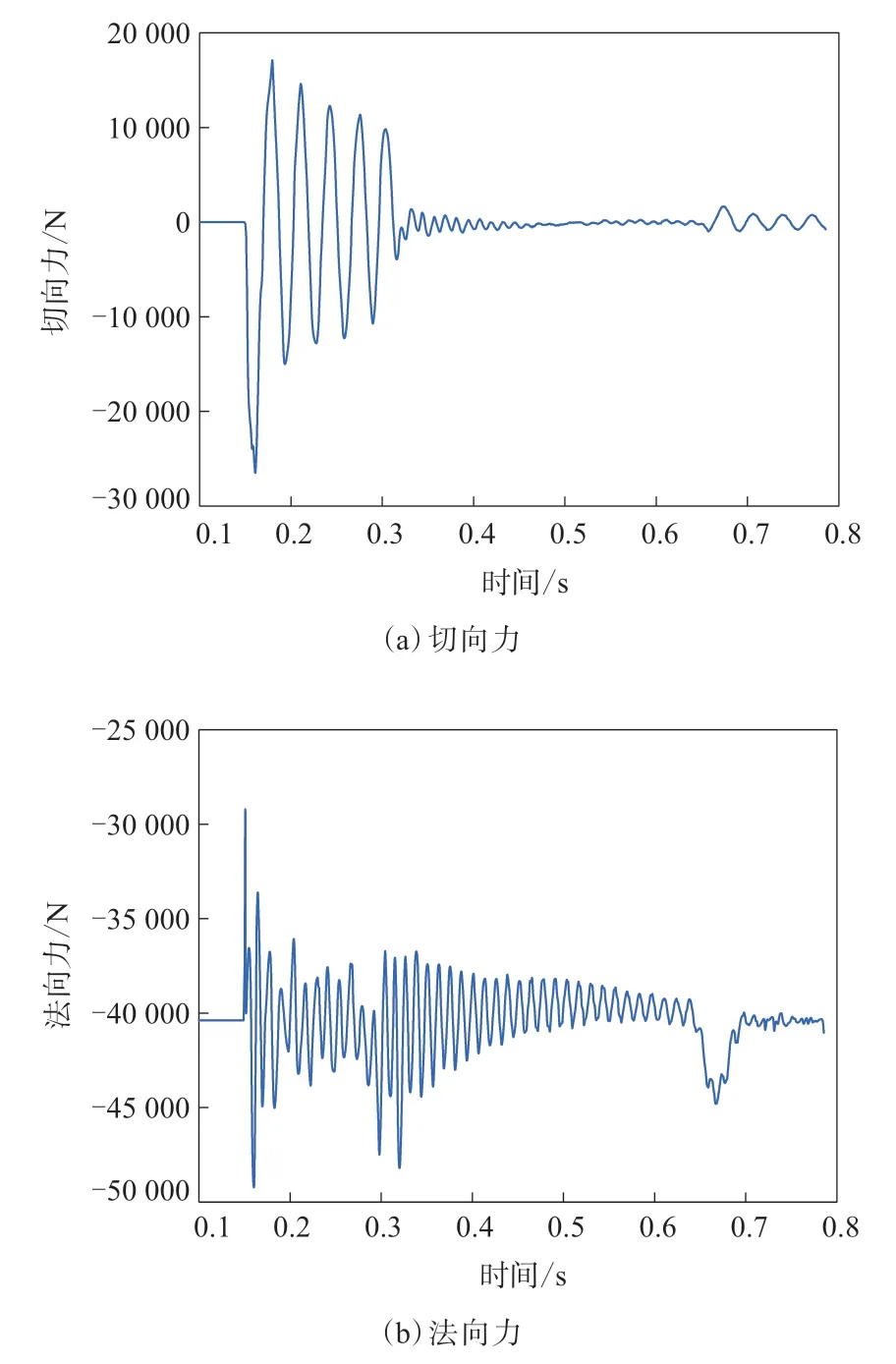
图11 半正弦路况轮胎切向力和法向力随时间的变化
轮胎驶出坡道时的力学特性同样重要,轮胎接触坡道和驶出坡道时的接触应力分布如图12所示。
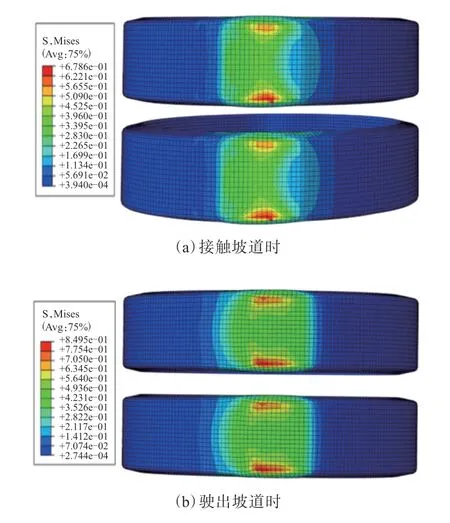
图12 轮胎接触坡道和驶出坡道时的接触应力分布
对比图6,7和11可以看出,增大摩擦因数,轮胎切向力从12 500 N增大到25 000 N,而法向力却不受影响,保持不变。由图11可以看出,在0.306 5 s时轮胎切向力迅速减小,且很快达到平稳,在0.675 9 s轮胎驶出坡道时,切向力有少许波动。由此可见,只在接触和驶出坡道时对轮胎切向力波动有影响,而在坡道上切向力的变化与在水平道路上基本一致。摩擦因数的增大没有影响法向力,但是受坡度的影响,坡度越大法向力增大越多。坡度不同,法向力在坡道上趋于平衡的速度明显不同,坡度越小越快趋于平稳,这正好与切向力相反。
从图12可以看出,高接触应力基本集中在轮胎接触面边缘处,并且高应力区前移。
2.4 减速带路况
在轮胎研究中,分析轮胎遇到障碍物时的力学特性至关重要。本工作采用减速带路况模拟轮胎遇到障碍物的情形,减速带模型如图13所示,轮胎-减速带模型如14所示。
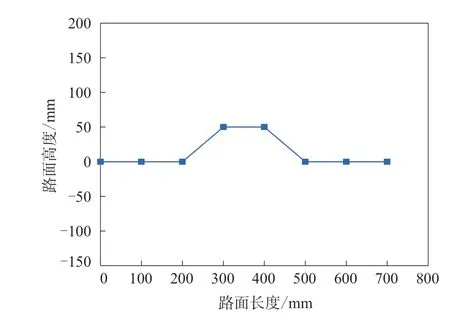
图13 减速带模型

图14 轮胎-减速带模型
同样轮胎先在水平道路起步,加载时长为0.330 s。在0.332 s时轮胎碰到减速带,在0.429 3 s时驶出减速带,然后又向前滚动一段时间,总时长为0.785 5 s,包括垂直负荷加载阶段(0.100 s)、垂直负荷加载稳定阶段(0.050 s)、水平道路行驶阶段、驶过减速带阶段(0.101 s)。垂直负荷为40 000 N,速度为20 km·h-1,摩擦因数为0.5。减速带路况轮胎切向力和法向力随时间的变化如图15所示。
从图15可以看出,轮胎切向力变化与过坡道时不同,在触碰到减速带时切向力迅速增大,在驶出减速带时又有增大。轮胎法向力在触碰到减速带时突然增大,在过减速带中间时比较平稳,但是在驶出减速带瞬间又迅速增大,这主要是由垂向惯性力导致的。
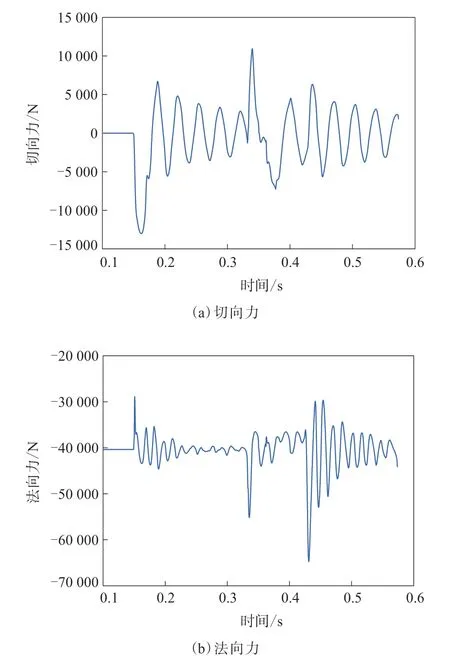
图15 减速带路况轮胎切向力和法向力随时间的变化
轮胎驶过减速带前后不同时刻接触应力分布如图16所示。
从图16可以看出,高应力区基本都集中在轮胎中心与边缘处。在减速带最高点时最大应力出现在轮胎接触面中心处。
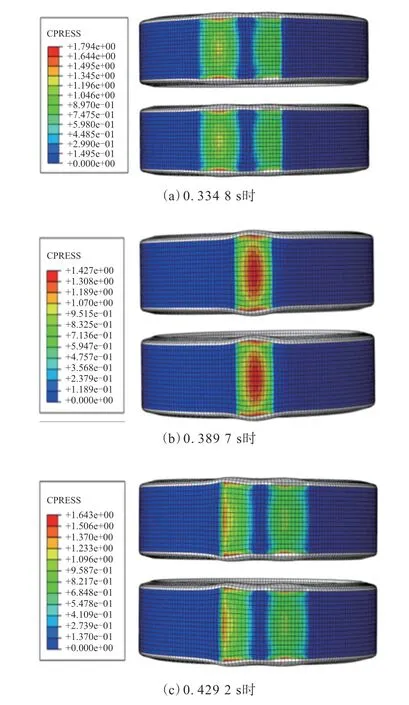
图16 轮胎驶过减速带前后不同时刻接触应力分布
2.5 减速带路况(非满载)
前面的研究都为轮胎施加40 000 N垂直负荷、速度为20 km·h-1的情况。下面考虑一种比较极端的情况,即履带车辆轮胎非满载、速度较快的情况,垂直负荷为30 000 N,速度设为40 km·h-1。
同样轮胎在水平道路起步,总时长为0.362 0 s,包括垂直负荷加载阶段(0.100 s)、垂直负荷加载稳定阶段(0.050 s)、水平道路行驶阶段和驶过减速带阶段。减速带路况(非满载)轮胎切向力和法向力随时间的变化如图17所示。
从图17可以看出,提高车速和减小负荷后,轮胎切向力的变化规律发生改变,但是最后还是会趋于平稳。在接触减速带时(0.274 1 s)轮胎切向力迅速增大,由于轮胎弹起,因此切向力为零。轮胎在以较高车速碰到障碍物时法向力会突然增大,在离开减速带时法向力达到100 000 N,并以较大的幅度缓慢趋于平稳。
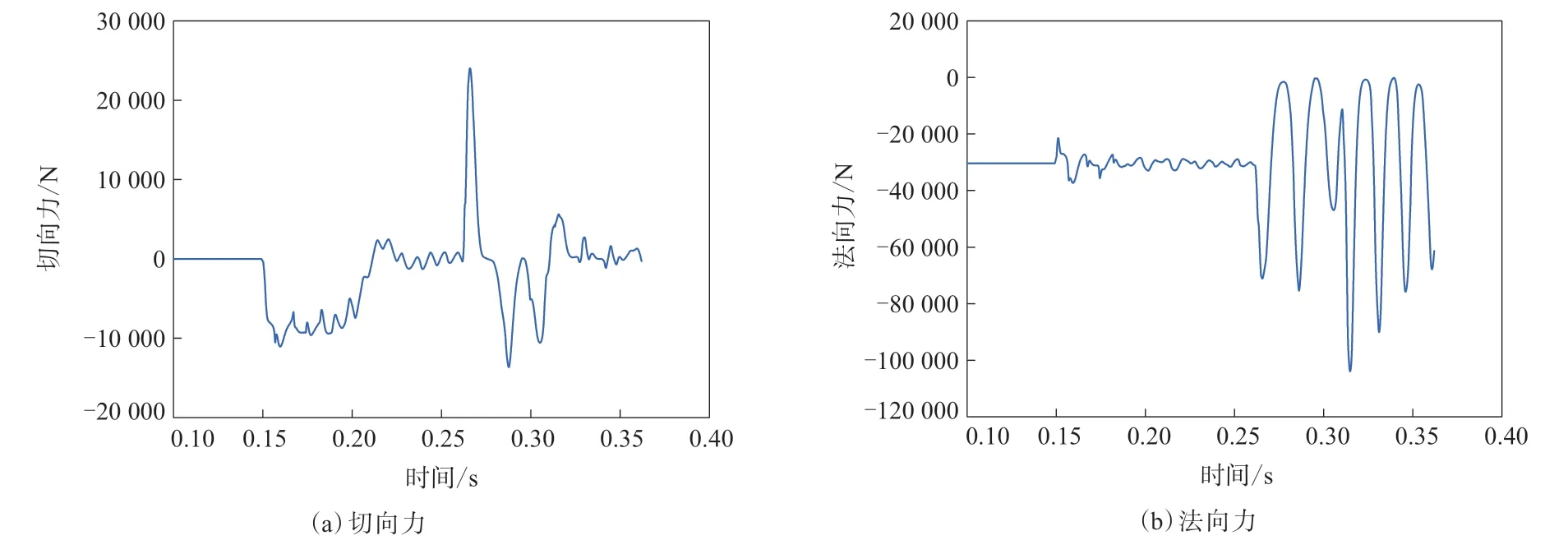
图17 减速带路况(非满载)轮胎切向力和法向力随时间的变化
3 结论
本研究基于履带车辆轮胎的结构和力学基础,使用非线性有限元分析技术,建立合理的轮胎有限元模型并进行仿真分析,研究轮胎在不同路况下的力学特性,通过仿真得到了不同路况下轮胎的切向力、法向力和接触应力的变化情况。
采用本方法可以快速仿真出轮胎在接近实际路况时的动力学特性,有助于设计出更符合实际路况要求的轮胎。
