基于TanDEM-X数据和改进三阶段算法反演森林冠层高度*

张国飞 章皖秋 岳彩荣

(西南林业大学林学院 昆明 650224)

森林是地球上面积最大的陆地生态系统，是全球生物圈中重要的一环，对维系整个地球的生态平衡发挥着不可替代的作用(Minh， 2020)。森林高度是森林最基本的结构参数之一，是重要的林分测量因子，对估算森林生物量、预测生物多样性等均具有重要意义(Sextonetal., 2009)； 然而，受森林分布、复杂地形条件、天气条件等因素制约，大范围开展森林高度测量一直是森林调查的技术难题。合成孔径雷达(synthetic aperture radar，SAR)是20世纪50年代末研制成功的一种微波传感器，具有获取植被表面极化和干涉模式数据的能力，被广泛用于森林结构和生物物理参数反演(Kumaretal., 2017)，其中合成孔径雷达干涉测量(interferometric synthetic aperture radar， InSAR)和极化合成孔径雷达干涉测量(polarimetric and interferometric synthetic aperture radar， PolInSAR)对森林体散射的形状、方向和垂直结构比较敏感，可获得不同植被高度下不同极化干涉复相干，大量用于森林结构监测(Cloudeetal., 1998； Papathanassiouetal., 2001)。

PolInSAR技术综合InSAR技术对体散射垂直结构的量度性以及PolSAR技术对体散射形状和方位的敏感性，能够生成任意极化散射机制下的复相干影像，各极化散射机制与森林结构特征相对应，为提取森林结构信息奠定了物理基础(Cloudeetal., 1998； Bamleretal., 1998； Papathanassiouetal., 2001)。Cloude等(1998)首次利用不同散射机制干涉优化算法估测了森林冠层高度。Treuhaft等(1996； 1999； 2000)提出的RVoG(random-volume-over-ground)模型是当前PolInSAR技术估测森林冠层高度机理模型的基础。Papathanassiou(2001)将极化干涉相干优化算法与RVoG模型相结合，提出了单基线RVoG复相干模型树高反演6参数法，并采用非线性迭代优化进行解算。Cloude(2003)基于复相干几何分布特征提出的RVoG复相干模型经典三阶段算法，简化了森林冠层高度估测的复杂性(Garestieretal., 2007； 2008； Chenetal., 2011； Luetal., 2013)。但由于受地形相位估计误差、纯体相干性估计误差的影响，经典三阶段算法反演森林冠层高度存在低估现象(Kumaretal., 2017； Kugleretal., 2015； Khatietal., 2015； Denbinaetal., 2016； 解清华等， 2015； 章皖秋， 2018)，如Khati等(2015)采用经典三阶段算法和TanDEM-X数据反演印度热带林区森林冠层高度，低估了7～10 m； 解清华等(2015)通过SAR数据仿真发现，在郁闭度较大的森林中各极化通道相位中心相对集中，地面相位中心偏高，森林冠层高度也被低估(RVoG模型通过求解地面相位中心与体散射相位中心之间的距离及体散射幅度估测森林冠层高度)。

RVoG模型经典三阶段算法根据L、P长波长的极化散射特征解算地面相位和体散射，在应用于短波长X 波段时会出现地面相位、纯体散射复相干估计不准确等问题，导致无法估测出合理的森林冠层高度。当前在轨星载SAR系统数据大多需要重轨获取，森林冠层高度估测时受时间失相干影响严重(Kumaretal., 2017； 范亚雄等， 2020)，而TanDEM-X星载数据采用一发双收模式对地物进行观测，零时间基线。鉴于此，本研究从X波段的极化散射机制出发，提出针对X波段数据RVoG模型经典三阶段反演算法的优化方法，并用TanDEM-X数据进行验证，以解决RVoG模型实际应用中模型成立条件难以严格满足、受地形影响导致森林冠层高度估测精度不高的问题。

1 研究区概况与数据

1.1 研究区概况

研究区位于云南省普洱市思茅区(22.8°N, 100.9°E)，地处北回归线附近，滇南热带与南亚热带的过渡地带，干湿季分明，年均气温15～20.3 ℃，年降雨量1 100～2 780 mm，平均海拔1 320 m。区内森林覆盖率67%，思茅松(Pinuskesiyavar.langbianensis)为主要森林类型，林内常混交红木荷(Schimawallichii)、刺栲(Castanopsishystrix)、小果锥(C.fleuryi)、茶梨(Annesleafragrans)和毛银柴(Aporusavillosa)等乔木树种(李江， 2011； 章皖秋， 2018)。

1.2 样地数据

选取思茅松人工林为研究对象，设置90块调查样地(图1)，其中思茅松纯林样地47块、混交林(以思茅松为主要优势树种的针阔混交林)样地43块。数据采集时间为2018年12月和2020年1月，采用分层随机抽样设置样地，大小为20 m×20 m，在样地范围内进行每木调查，起测胸径5 cm，调查因子包括树种、树高、胸径、郁闭度和地况，见表1。

图1 研究区位置(上)与样地分布(下)Fig. 1 Location of study area (top) and plot distribution (bottom)

表1 调查样地数量和林分参数Tab.1 Number and stand parameters of field plots

森林高度估测基于对森林冠层微波散射中心位置的推断，估测值理论上与森林冠层表面高度最接近，但考虑到地面测量难度，本研究以样地内单木树高算术平均值作为森林冠层高度的替代值。研究区森林高度主要分布在10～20 m，平均高度15.7 m(纯林平均高度14.2 m，混交林平均高度17.3 m)，最小高度3.6 m，最大高度24.0 m。

1.3 卫星数据

采用零时间基线的TerraSAR-X和TanDEM-X全极化干涉产品，产品参数描述见表2。

图2所示为TDX CoSSC产品主辅图像Pauli假彩色合成图(HH-VV、HV+VH、HH+VV)。2种数据集分布于HH、HV、VH和VV 4个极化通道。在研究区范围内，地表产生的面散射、树枝和树叶随机定向产生的体散射、地表-树干相互作用产生的二面角散射3种散射成分容易出现。

表2 SAR 数据描述Tab.2 Description of SAR data

图2 主(左)辅(右)图像Pauli假彩色合成Fig. 2 Pauli colour composite of master (left) and slave (right) images红: HH-VV； 绿: HV+VH； 蓝: HH+VV。Red: HH-VV; Green: HV+VH; Blue: HH+VV.

2 研究方法

2.1 RVoG模型

Treuhaft等(1996； 1999； 2000)提出一种带有地面回波的随机方位体积层模型(RVoG)森林高度反演方法，森林被视为覆盖在地表的随机体粒子层，包含大量随机分布且相互独立的体散粒微粒。

在雷达波入射角为θ的二层RVoG模型(图3)中，地表被认为是雷达波无法穿透的表面散射层，高度为Z0，引起地面相位为φg，植被厚度为hv，森林冠层高度为Z0+hv。假定植被层的散射能量随高度增加呈指数变化，消除配准误差、大气去相干等影响后，基于RVoG模型的极化干涉复相干γ(ω)表示(Treuhaftetal., 1999； Luetal., 2013； Kugleretal., 2015)如下：

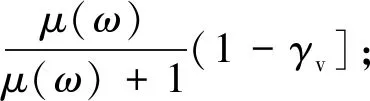
(1)

(2)

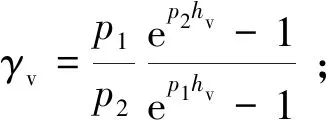
(3)

(4)

图3 RVoG 模型Fig. 3 RVoG model

在RVoG复相干模型中，θ、λ、Δθ、kz可通过SAR平台系统参数代入获得；φg、μ(ω)、hv、σ可通过求解RVoG复相干模型来估测森林冠层高度(李廷伟等， 2009； 章皖秋， 2018)。

2.2 不同优化改进的三阶段算法反演森林冠层高度

本研究设计4种方法反演森林冠层高度，主要步骤见图4。方法1采用经典三阶段反演算法，作为基准模型； 其他3种方法分别为地面相位优化估计、纯体散射复相干优化估计和低估补偿改进三阶段反演算法，是一个逐步改进的优化过程，以检验优化方法在森林高度估测方面的性能增益。地面相位优化估计、纯体散射复相干优化估计处于三阶段反演算法的第二、三阶段，低估补偿改进算法针对三阶段反演算法估测的地面相位可能高于实际地表导致的高度低估情形，3种优化方法亦可单独使用。图4中阴影步骤为方法改进部分。

2.2.1 方法1——经典三阶段反演算法 经典三阶段算法是一种基于RVoG模型的几何分布特征反演算法，分为3个阶段(陈兵等， 2008)。

第一阶段： 各极化复相干直线拟合。根据式(1)，各极化复相干(包括HH、HV、VH、VV、HH+VV、HH-VV、LL、RR、OPT1、OPT2、OPT3、PDhigh、PDlow等13种)在复平面单位圆(complex unit circle，CUC)的轨迹呈直线形式。三阶段算法采用总体最小二乘法拟合复相干拟合直线的参数(Minhetal., 2014； Cloude， 2015)，复相干拟合直线(complex fitting line，CFL)与CUC的2个交点的相位作为候选地面相位，见图5。

第二阶段： 从候选交点中确定地面相位。有效地体散射幅度比μ(ω)可以克服这一模糊性，即当μ(ω)→∞，γ(ω)仅包括林下地表的面散射。经典三阶段算法选择拟合直线上距离γHV较远的交点作为林下地表的面散射，其相位为地面相位(Cloud， 2003； Kugleretal., 2015)。

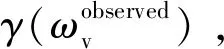
图4 4种方法的主要步骤Fig. 4 Main procedures for the four different methods

图5 复平面单位圆内相干线的几何表示Fig. 5 The geometrical representation of coherence line inside the complex unit circle

为了检验各优化方法在森林高度估测方面的性能增益，本研究4种方法均采用固定的消光系数(σ)。已有研究发现，热带阔叶林和针叶林的消光系数为0.1～0.9 dB·m-1(Hajnseketal., 2009； Caicoyaetal., 2012)，反演森林高度时，针叶林的消光系数固定值为0.2 dB·m-1(Caicoyaetal., 2012)、热带森林的消光系数固定值为0.3 dB·m-1(Hajnseketal., 2009)和0.4 dB·m-1(廖展芒， 2019)。本研究中，思茅松林消光系数取0.2 dB·m-1； 另外，hv限制在5～30 m之间。

在方法1中，估测的森林冠层高度称为Classic_H。

2.2.2 方法2——地面相位优化的三阶段反演算法 该方法旨在检验地面相位优化的三阶段反演算法对森林冠层高度估测的影响，算法其余部分与方法1相同。

经典三阶段算法中，地面相位通过比较γHV与候选交点的距离进行估测(Papathanassiouetal., 2001； Kriegeretal., 2007； 解清华等， 2015)，但受地形起伏和枝叶生长方向不确定性的影响，X波段HV极化通道不一定在林冠顶部，有可能接近地面(Cloude， 2015； Denbinaetal., 2016)，同时X波段极化复相干分布相对集中，并趋于某一交点(Kriegeretal., 2007； Kugleretal., 2015)，在这2种情况下，经典三阶段算法可能错误估测地面相位。本研究参考γPDlow估测地面相位，γPDlow和γPDhigh是极化空间相位差异最大的极化干涉复相干，γPDlow相位中心接近森林底部(Flynnetal., 2002； Kriegeretal., 2007； 解清华等， 2015)，同侧的交点应该是地面层交点。

具体步骤如下：

第一步，计算各观测复相干值与2个交点之间的相位差，并分别按从小到大排序：

Δφi,ω=abs{arg[(γ(ω)e-jφi]}，i=1,2；

(5)

(6)

第二步，若γPDlow在Rank 1中位居前3位，则φg=φ1； 若γPDlow在Rank 2中位居前3位，则φg=φ2； 若2组排序均没有超过前3位，则φ1和φ2分别作为候选地面相位，得到2个冠层高度估测值，选择估测值在合理范围内的候选地面相位作为φg输出(Cloude， 2003； 章皖秋， 2018)。

在方法2中，估测的森林冠层高度称为Improve_H1。

2.2.3 方法3——纯体散射复相干优化的三阶段反演算法 该方法旨在检验纯体散射复相干优化的三阶段反演算法对森林冠层高度估测的影响，算法其余部分与方法2相同。

经典三阶段算法中，γHV作为纯体散射复相干观测值，其在拟合直线上的垂直投影作为纯体散射复相干估计值，此时，μHV接近0，γHV与地面γ(wg)距离最远(Papathanassiouetal.， 2001； 章皖秋， 2018)，但垂直投影会改变纯体散射复相干有效观测值的模值和相位，容易引入误差(Cloude， 2015； 章皖秋， 2018)，见图6。因此，本研究提出纯体散射优化估计，即从各极化复相干中筛选出纯体散射复相干观测值，并采用模值不变投影方法估计纯体散射。

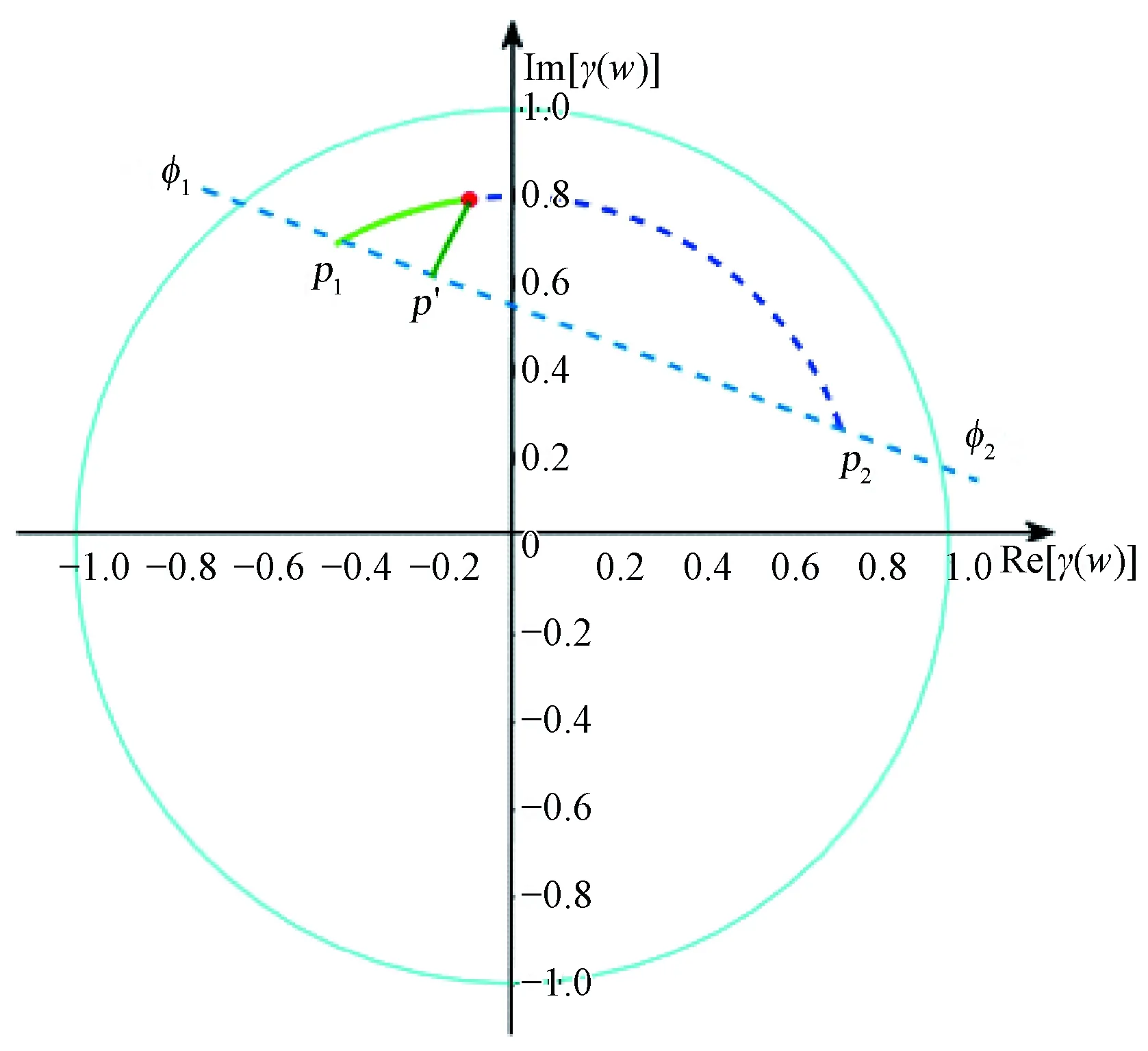
图6 模值不变方式投影Fig. 6 The projection of unchanged module of complex coherence

具体步骤如下：

第二步，采用模值不变投影方法估计纯体散射γ(ωv)。首先，以坐标原点为圆心、以体散射有效观测值γ(ωobserved)的模值为半径作圆； 然后，计算圆与拟合直线(CFL)的交点p1和p2，取离垂直投影点p′距离较小的交点p1作为纯体散射γ(ωv)，如下式：

(7)

若体散射观测值γ(ωobserved)距拟合直线距离很近，则p1与p′相差不是很大； 若圆与拟合直线没有交点，则用垂直投影点p′替代，如图6所示。

在方法3中，估测的森林冠层高度称为Improved_H2。

2.2.4 方法4——低估补偿改进的三阶段反演算法 该方法旨在检验低估补偿改进的三阶段反演算法对森林冠层高度估测的影响，算法其余部分与方法3相同。

X波段波长短，在森林区域易出现穿透不深的情况，尤其在局部入射角较大的背向雷达波波面上或林冠茂密的区域，经典三阶段算法估测的地面相位可能高于实际地表，造成森林冠层高度低估(Parksetal., 2013； 解清华等， 2015)。因此，本研究基于γPDlow相位更接近地表的假设条件，提出一种三阶段低估补偿算法，以改善X波段SAR数据估测时森林冠层高度被低估的现象。

具体步骤如下：

第二步，判断地面相位位置。如果 Δφv,g≥Δφv,PDlow，地面相位处于γPDlow复相干相位下方，森林冠层估测高度不需要补偿； 如果Δφv,g<Δφv,PDlow，地面相位估计值高于γPDlow相位，森林冠层估测高度需要补偿，进入下一步。

第三步，高度补偿。计算地面相位与γPDlow的相位差，并转换为高度差，将高度差加Improved_H2上，如下式：

(8)

图7 研究区的地面相位Fig. 7 Estimated ground phase of study areaa. 参考γHV的地面相位Ground phase estimated referring to γHV； b. 参考γPDlow的地面相位Ground phase estimated referring to γPDlow.

在方法4中，估测的森林冠层高度称为Compensated_H。

采用皮尔逊相关系数(r)、均方根误差(RMSE)和偏离率(bias)对所有算法进行检验：

(9)

(10)

(11)

3 结果与分析

3.1 地面相位优化

根据RVoG模型，地面相位是由林下地表高程引起的相位。林下地表高程属于连续表面，地面相位形成的条纹应清晰光滑、有规律性。与经典三阶段算法估测的地面相位(图7a)相比，优化三阶段算法估测的地面相位(图7b)条纹清晰、斑点少，表明以γPDlow相位为参考的地面相位优化估计有利于改善森林冠层高度估测。

3.2 森林冠层高度估测

经典三阶段反演算法和TanDEM-X SAR数据反演森林冠层高度出现低估现象，90块思茅松样地偏离率为-26.20 m，Classic_H与样地实测高度的相关性低，精度不高(r=0.11，RMSE=7.16 m)。图8a1、b1显示，大部分散点分布在y=x线以下。

与Classic_H相比，地面相位优化可改善森林冠层高度低估现象，偏离率从-26.20 m提高至-9.19 m，Improved_H1与样地实测高度的相关性和精度均有所提高(r=0.46，RMSE=4.00 m)。图8a2、b2显示，大部分散点分布在y=x线两侧，说明地面相位优化方法有效。

与Improved_H1相比，纯体散射复相干优化的三阶段反演算法在森林冠层高度低估和模型反演精度方面改善效果不明显(bias从-9.19 m提高至-7.31 m，RMSE从4.00 m提高至3.57 m)； 但筛选体散射复相干观测值和模值不变投影方法使估测高度与实测高度的相关性优化(r从0.46提高至0.62)，说明个别样地的估测精度有所提高(图8a3、b3)。

与Improved_H2相比，低估补偿改进的三阶段反演算法可进一步改善森林冠层高度低估现象，偏离率从-7.31 m提高至-1.69 m，Compensated_H与样地实测高度的相关性和精度有所提高(r=0.79，RMSE=2.56 m)(图8a4、b4)。

从4次试验的反演结果看，与思茅松混交林相比，三阶段优化算法对思茅松纯林的适应性更好。在方法1、2、3中，增加思茅松混交林样地后，总体样本森林冠层高度与实测高度的皮尔逊相关系数降低，均方根误差精度降低； 在方法4中，增加思茅松混交林样地后，总体样本森林冠层高度与实测高度的皮尔逊相关系数没有太大变化，而均方根误差精度降低(表3)。

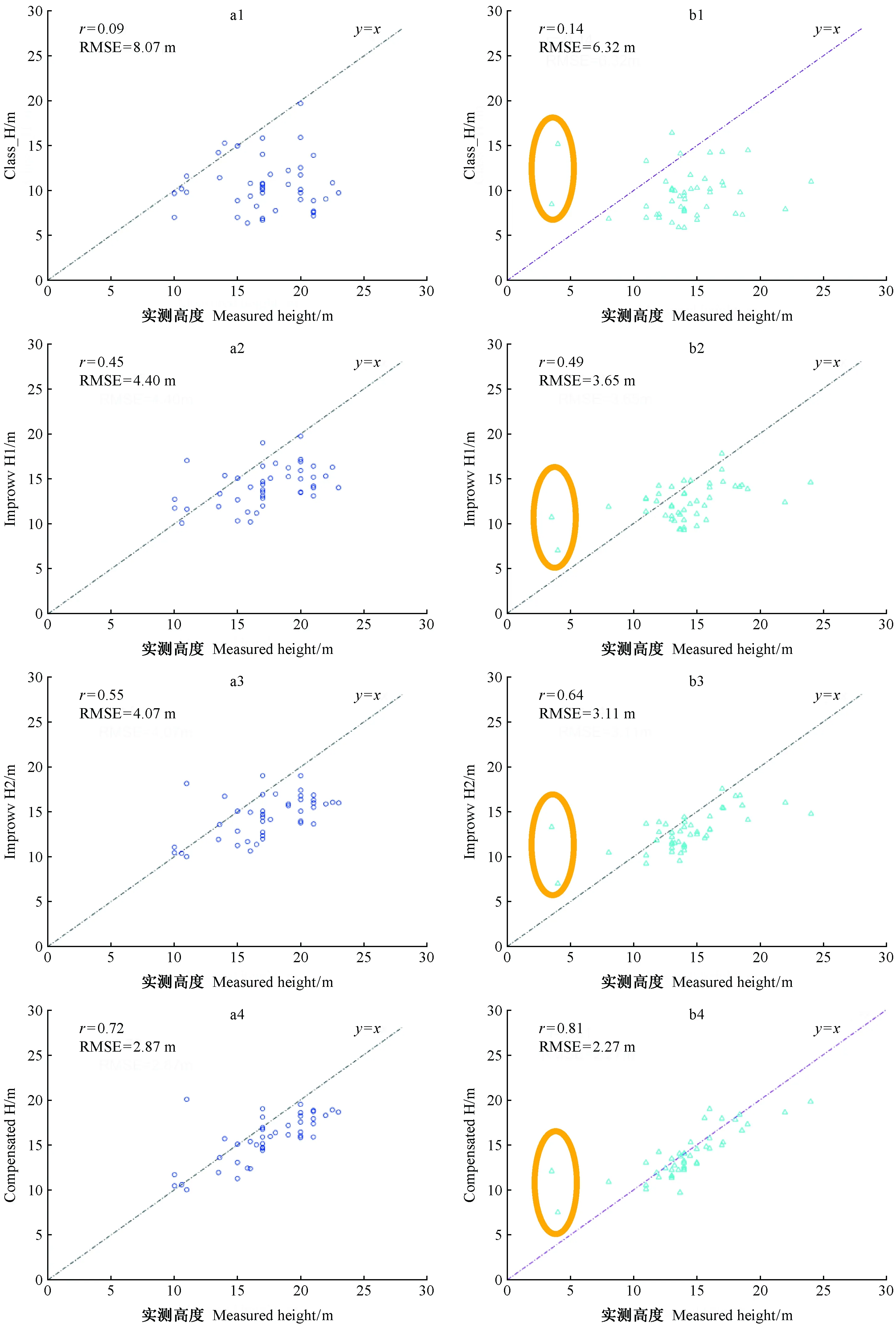
图8 估测高度和样地实测高度的散点图Fig. 8 The scatter plots between estimation heights and measured heightsa1、a2、a3和a4为思茅松混交林样地； b1、b2、b3和b4为思茅松纯林样地； 橙色圈内的样地为思茅松幼龄林。a1,a2,a3 and a4： plots in P. kesiya var. langbianensis mixed forests； b1,b2,b3 and b4： plots in P. kesiya var. langbianensis pure forest； the plots in orange circle is young P. kesiya var. langbianensis forest.

总体结果表明，在4种森林冠层高度估测方法中，本研究提出的优化方法能够逐步提高估测精度。图9为森林冠层估测高度Compensated_H分布。从反演结果来看，研究区森林冠层高度主要分布在16～22 m之间(图9b)，与研究区2016年森林二调数据样地林分平均高度(16～20 m)具有一致性(云南省林业调查规划院， 2016)。

4 讨论

方法1经典三阶段反演算法估测森林冠层高度存在低估现象，可能是X波段穿透性差引起地面相位和纯体散射复相干估计不准确导致的(解清华等， 2015； Denbinaetal., 2016； 章皖秋， 2018； Parksetal., 2013)。针对地面相位估计不准确的问题，本研究提出参考γPDlow估计地面相位，结果发现优化后的地面相位比经典三阶段算法条纹更清晰。针对纯体散射复相干估计不准确的问题，本研究提出纯体散射复相干优化估计，从各极化复相干中筛选出纯体散射观测值，采用模值不变投影方法估计纯体散射。方法2和3均可改善三阶段反演算法的森林冠层高度估测精度。

森林结构是森林冠层高度估测精度的主要影响因素之一。在幼龄林或稀疏林分中，郁闭度较小，雷达波大部分穿透地面，森林冠层体散射在回波信号中占比较小，纯体散射复相干的一部分是由地面复相干引起的，导致森林冠层高度异常估计(解清华等， 2015； Denbinaetal., 2016； 章皖秋， 2018； Parksetal., 2013； Sadeghietal., 2016)，如研究区2块幼龄林样地(林分平均高度为4 m和3.6 m)的高度估测出现异常(图8b中已标注)。在冠层密度中等、垂直结构单一的针叶纯林林分中，冠层结构相似，外形近似随机散射粒子层，回波信号主要来自整个冠层，采用优化三阶段反演算法和TanDEM-X SAR数据估测的森林冠层高度接近实测高度。在垂直结构复杂林分中，如针阔混交林，呈现2层或多层树冠结构，郁密度较大，雷达散射回波信号由多林层回波的相干叠加，散射相中心位置随林层结构不同而变化，森林冠层高度估测值与实测值的关系复杂多变。因此，当稀疏林分中郁闭度较小或垂直结构复杂林分中郁密度较大时，三阶段算法反演森林冠层高度可能会出现异常，估测精度不高(章皖秋， 2018)。从本研究反演结果看，与思茅松混交林相比，三阶段优化算法对思茅松纯林的适应性更好。在方法4中，思茅松纯林冠层估测高度与实测高度的反演精度(r=0.81，RMSE=2.27 m)优于思茅松混交林(r=0.72，RMSE=2.87 m)。后续研究中，针对稀疏林地或裸地，可通过对地物的准确分类，剔除非林地区域和近“裸”林分，提高估测精度； 针对垂直结构复杂林分，可利用多频多时相SAR数据联合探索复杂冠层结构与微波散射机制的关系； 针对估测值异常现象，可研究不同地面单元的自适应估测方法，如通过空间滤波和重采样等降低空间分辨率技术，用区域平均值、中值等统计值代替异常估测的地面分辨率单元，减小局部估测偏差，为大面积中、低比例尺度的森林冠层高度提供基础数据。

表3 4种三阶段反演算法的验证结果Tab.3 Validation results of the three-stage inversion algorithm from all approaches

图9 研究区域(部分)估测森林冠层高度分布(a)和直方图(b)Fig. 9 Predicted maps(parts) of Compensated_H in the study area

Khati等(2015)采用经典三阶段反演算法和TanDEM-X数据反演印度热带林区森林冠层高度，17块样地森林冠层估测高度出现低估现象(-7～-10 m)，RMSE为7.60 m，与本研究中方法1结果相当。冯琦等(2016)利用机载X波段HH干涉数据和SINC模型估测地形平缓的内蒙古白桦(Betulaplatyphylla)林冠层高度，估测高度与LiDAR测量高度的相关系数为0.86，RMSE为2.74 m，高于本研究方法4估测结果，原因可能源于本文研究区地形起伏较大。Kugler等(2015)提出一种地形校正的三阶段反演算法，用2种不同入射角的TanDEM-X SAR数据解决透视收缩问题，用外部DEM优化地面相位估计和降低坡度对估测高度的影响，估测高度和LiDAR测量高度的相关系数为0.94，RMSE为1.32 m； 但地形校正的三阶段反演算法需要数据较多，不利于实际应用。Kumar等(2017)采用TanDEM-X数据和三阶段反演算法估测印度北方坎德邦的Barkot和Thano森林，估测高度与实测高度的相关系数为0.74，RMSE为3.19 m，相比本研究方法4估测结果稍差。

综上所述，优化三阶段反演算法估测森林冠层高度仅以单基线全极化SAR数据为数据源，在大多数地区均可以获得较高估测精度。

5 结论

采用经典三阶段反演算法和TanDEM-X SAR数据估测森林冠层高度时，由于X波段波长短，穿透力差，存在地面相位和纯体散射复相干估计不准确的问题，导致无法估测出合理的森林冠层高度。本研究从X波段的极化散射机制出发，对RVoG模型经典三阶段反演算法进行优化和改进，提出适合X波段SAR数据的优化三阶段反演算法，包括地面相位、纯体散射复相干优化和低估补偿算法，以普洱市思茅松林为研究对象，获得较好估测精度，冠层估测高度和实测高度的相关系数在0.72～0.81之间，均方根误差在2.00～3.00 m范围内。优化三阶段算法反演精度较经典三阶段算法有了较大提高，利用该方法和TanDEM-X SAR数据可实现大范围森林高度的估测。