Dtw算法在无参考图像序列像素重构中的应用

朱兴宇，时庆涛

(1. 长春工业大学应用技术学院，吉林 长春 130012；2. 长春工业大学人文信息学院，吉林 长春 130012)

1 引言

近年来随着科技的不断发展，图像与视频的分辨率也越来越高。老旧的图像及视频由于分辨率太低而无法提取有效的信息，因此需使用必要的手段重构图像或视频的像素。DTW算法作为经典的动态时间规整算法，可以通过对像素之间最优路径的计算，完成人们对原始图像或视频中的无参考图像序列像素的重构。从而满足人们对图像的高分辨率需求。

针对此问题，相关领域专家已经得到了一些研究成果。刘迪等人提出基于核密度估计的无参考图像序列像素重构方法。该方法首先基于像素的系统原理分析像素距离，再通过直方图与邻域核密度算评价分析结果。最后利用GM-APD激光雷达对无参考图像序列像素之间的距离进行测量，从而实现无参考图像序列像素的重构。该方法未能提取无参考图像序列像素进行特征属性，因此该方法无法有效检测出像素的路径衰减曲线。吴磊等人提出基于多尺度递归网络的无参考图像序列像素重构方法。该方法首先计算获取像素的多尺度特征映射单元；再基于获取的像素映射单元构建多尺度递归网络的图像像素分辨模型；最后通过亚像素卷积重构方法重构无参考图像序列像素。但是，该方法由于未能利用基尼指数划分无参考图像序列像素数据集的节点数据，因此该方法的像素覆盖性能差。杨春玲等人提出基于多维度参考帧的无参考图像序列像素重构方法。该方法首先构建一个双稀疏像素重构模型，采用互频信号与拉普拉斯加权法来刻画像素帧的稀疏特性；引入多维度参考帧，对时间与缩放维度的像素帧进行匹配；最后利用搜索算法实现对无参考图像序列像素的重构。该方法由于未能训练采集的数据，因此该方法的重构误差高。

为解决上述传统方法存在的问题，提出基于DTW算法的无参考图像序列像素重构方法。

2 像素去噪

2.1 噪声模型

设定无参考图像序列像素中的脉冲噪声为

Y

，表达方式如下式所示

Y

=

X

+

v

(1)

式中，

X

为无参考图像序列像素，

v

为像素中的噪声。假定原始图像为一个8×8的无参考图像序列像素块，将其进行扩展使其成为一个1×64的一维信号。

2.2 稀疏滤波

利用K-SVD字典训练算法，通过像素奇异值的分解对无参考图像进行稀疏滤波表示。

设定

X

为原始图像的序列像素，图像中的加性高斯噪声为

Y

，无参考图像的噪声标准差用

σ

表示，通过计算获取的加性高斯噪声的概率如下式所示

(2)

式中，

P

表示获取的加性高斯噪声的概率，依据图像的局部相关性获取无参考图像的像素噪声分布，过程如下式所示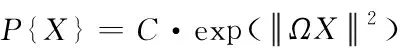

(3)

式中，

Ω

为无参考图像中噪声的变换处理过程，

C

为变换过程中的常数。此时若

D

为

Ω

的逆矩阵，且

D

=

Ω

，那么

D

为完备字典。若

D

为

Ω

的广义逆矩阵，那么

D

=

Ω

，

D

为过完备字典。由此可知，

DΩX

=

X

，且

ΩX

=

α

，

Dα

=

X

，

α

为系数。设定逆矩阵

D

中有

n

个原子，表示为

D

={

d

，

d

，…，

d

}。

X

则为

n

个原子的线性组合。这时若

D

为固定值时，通过追踪算法可获取

α

。

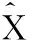
(4)

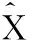
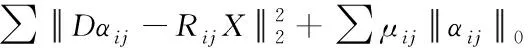
(5)

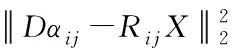
(6)

式中，

C

为转化常数。通过上式完成对图像的稀疏性目标优化。

2.3 去噪

由于无参考图像中含有未知的脉冲噪声，因此图像中的部分像素点会被噪声取代，导致无参考图像中的像素点无法正常提取信息。因此脉冲噪声在进行滤波检测时主要分为噪声检测、图像滤波两个部分，经过噪声检测的图像，获取的噪声标识矩阵如下式所示

(7)

式中，

x

为图像的噪声标识矩阵。

基于MK-SVD法对图像进行噪声检测，并将检测结果应用于脉冲噪声滤波，将式(5)改为下式

(8)

3 像素重构

基于随机森林原理对去噪后的无参考图像序列像素进行特征属性的提取，最后依据动态时间规整(DTW)算法对无参考图像序列像素进行重构。

3.1 提取像素特征属性

首先采集去噪后的无参考图像序列像素中的数据信息，运用bootstrapping方法有放回地抽取采集数据，构建数据集

D

，过程如下式所示

(9)

式中，

m

表示数据的采样次数，通过决策树原理对采集的数据进行训练，获取不剪枝的CART树。这时设定无参考图像序列像素中有

n

个特征，在每棵树的节点抽取

n

′(

n

′≤

n

)个特征，引入随机属性，利用基尼指数对数据集的每一个节点数据进行划分。过程如下式所示

(10)

式中，

p

为样本数据集

D

中的第

k

类样本数据所占比例，且

p

(

k

=1，2，…，|

K

|)。无参考图像序列像素的特征属性

a

的基尼指数表现形式如下式所示

(11)

式中，

a

为无参考图像序列像素的特征属性，且属性中具有

V

个可能的取值为{

a

，

a

， …，

a

}，像素特征属性

a

所划分的数据子集为

D

。获取的最优划分属性如下式所示

a

=arg min

Gini

-

index

(

D

，

a

)

(12)

通过上述的计算结果完成对无参考图像序列像素特征属性的提取。

3.2 基于DTW算法完成像素重构

基于动态时间规整(DTW)算法对提取的无参考图像序列像素特征属性进行规整，获取无参考图像序列像素的最佳路径，以此完成无参考图像序列像素的重构。

DTW算法作为最常用的非线性规整技术，是计算无参考序列间相似度的常用计算方法之一。该算法是运用动态规划思想，依据即时弯折函数在无参考图像的序列像素范围内自动寻找一条最佳的路径。无参考图像序列像素的重构分为计算像素对应帧之间的距离与寻找最佳路径两个部分，具体过程如下：

1)假定无参考图像序列像素的测量序列为

T

={

T

(1)，

T

(2)，…，

T

(

N

)}，像素的参考序列为

R

={

R

(1)，

R

(2)，…，

R

(

M

)}，

m

，

n

分别为

R

，

T

中的任意帧号，

R

(

n

)，

T

(

m

)分别为像素对应序列中第

n

，

m

帧特征矢量，且

n

的取值范围在1至

N

之间，

m

的取值范围在1至

M

之间。设

d

[

T

(

n

)，

R

(

m

)]为像素时间序列中两个数据点之间的距离，并将其看作

n

与

m

之间的异性量化表示。当像素的特征矢量越相似，获取的值就越接近于0，

n

，

m

之间的差距越大，获取的值就越大。无参考图像序列像素的距离函数要依据实际采集的距离度量来设定，在计算无参考图像序列像素中不同数据之间的差异时，要利用常用的二阶距离函数(欧氏距离)对其进行计算，首先设定需要计算的两组数据分别为

x

(

n

)与

y

(

n

)，且

n

=1，2，…，

N

，具体计算过程如下式所示

(13)

式中，

d

(

x

，

y

)为两组数据之间的距离。由于无参考图像序列像素中不同时间序列之间的欧式距离并不相同，因此要依据上述计算结果构建欧氏距离的

N

×

M

距离矩阵，过程如下式所示

(14)

由此可计算出无参考图像序列像素中各数据点之间的距离。

2)构建一个二维直角坐标系，将测试模板中像素的各个帧号放入坐标的中，并对像素帧号的位置进行相互连接获取坐标的横纵向网格。将寻找最佳路径时所经过的网格点设定为像素计算距离所需要的帧号，当

T

的第

n

个样本数据与

R

的第

m

个样本数据一致时，获取的斜率

k

是一条为1的直线，但当二者不一致时，二者之间的对应点不存在一条直线上，而是在一条规整的曲线上。在搜索无参考图像序列像素的最佳路径时，为了使获取的路径不过分倾斜，因此要将

k

的取值设定在0

.

5到2的范围内。假定计算每条路径达到的总累计距离为(

n

，

m

)，其中的最小累计距离为该无参考图像序列像素的最佳路径。若限定范围内的任意网格点(

n

，

m

)有且仅有一条路径可通过该数据点，但该网格点的前一格点可能为(

n

-1，

m

)、(

n

-1，

m

-1)或(

n

-1，

m

-2)中的任意一个，这时获取的路径累积距离如下式所示

D

(

n

，

m

)=

d

[

T

(

n

)，

R

(

m

)]+min[

D

(

n

-1，

m

)，

D

(

n

-1，

m

-1)，

D

(

n

-1，

m

-2)]

(15)

式中，获取的路径累积距离为

D

(

n

，

m

)。由此可知，从(

n

，

m

)出发搜索(

n

，

m

)，…，(

n

，

m

)，将搜索的结果储存到相应的像素帧匹配距离

d

[

T

(

n

)，

R

(

m

)]中，最后将网格点中数据搜索到(

n

，

m

)时，将其进行保留并作为该无参考图像序列像素的最佳路径，完成对无参考图像序列像素的重构。最佳路径的约束示意图如图1所示。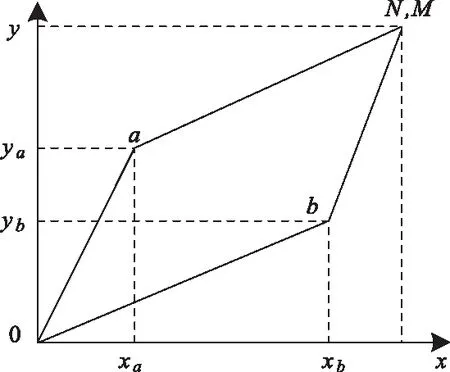

图1 无参考图像序列像素最佳路径约束示意图

4 实验

为了验证上述方法的整体有效性，需要对此方法进行测试。

4.1 实验结果及分析

分别采用DTW算法在无参考图像序列像素重构中的应用(方法1)、基于像素邻域核密度估计的无参考图像序列像素重构方法(方法2)、基于多尺度递归网络的无参考图像序列像素重构方法(方法3)进行测试；

1)在无参考图像序列像素中添加一组杂乱数据，对方法1、方法2以及方法3的重构图像的像素路径衰减曲线进行检测，检测结果如图2所示。

图2 不同方法重构图像的像素路径衰减曲线检测结果

依据图2可知，方法1能够有效检测出重构图像像素的路径衰减曲线，并且能够将检测出的曲线与标准的路径衰减曲线相接近，这主要是因为方法1利用了随机森林原理对无参考图像序列像素进行了特征属性的提取，因此该方法在像素中有杂乱数据的情况下，依然能够精确地检测出重构图像像素的路径衰减曲线。

2)依据计算机仿真技术模拟一个无参考图像序列像素，利用方法1、方法2以及方法3对无参考图像序列像素进行重构，测试三种方法在不同网络峰值下的像素覆盖性能，测试结果如表1所示。

表1 不同像素重构方法的像素覆盖性能测试结果

依据表1可知，方法1的像素覆盖性能要高于方法2以及方法3，虽然方法2在网络峰值低于120bit/s时的像素覆盖率能够与方法1持平，但随着网络峰值的增加方法2的像素覆盖率呈急速下降趋势。这主要是因为方法1利用基尼指数对无参考图像序列像素数据集中的节点数据进行划分，因此该方法在网络峰值较高的情况下依然能够准确地对无参考图像序列像素进行全面覆盖。

3)依据上述测试结果，对三种像素重构方法的平均峰值信噪比与结构相似度进行测试，以此检测三种方法的平均重构误差，检测结果如表2所示。

表2 不同方法的平均重构误差测试结果

依据表2可知，方法1的平均峰值信噪比和结构相似度要优于方法2和方法3，这主要是因为方法1运用了bootstrapping方法对无参考图像序列像素进行了有放回地的数据采集，并基于决策树原理对采集的数据进行训练，获取不剪枝的CART树。因此方法1检测出的平均峰值信噪比与结构相似度都要高于其它方法，从而降低该方法的平均重构误差。

5 结束语

针对传统像素重构方法中出现的问题，提出DTW算法在无参考图像序列像素重构中的应用。该方法首先利用MK-SVD法对像素中的噪声进行去噪处理；再利用随机森林原理提取像素的特征属性；最后基于动态时间规整(DTW)算法获取像素的最佳路径，从而完成无参考图像序列像素的重构。该方法由于在像素去噪时还存在一定问题，因此今后会针对这一缺陷继续完善该方法。