组合式建筑几何轮廓定标误差识别建模仿真
2022-07-20赵继平
赵继平,林 伟
(电子科技大学成都学院,四川 成都 611731)
1 引言
建筑物的三维建模属于计算机图形学、视觉领域、虚拟现实研究领域的核心问题。建筑物建模在智慧城市建设、城市规划工作中是不可缺少的环节。组合式建筑物结构主要通过2个或者多于2个的规则几何结构构成,目前针对建筑物的建模研究不在少数,但针对组合式建筑建模方面的研究资料较少。组合式建筑是近几年各个国家建筑工程领域重点研究的建筑类型,其能够使用2个或多个几何结构设计成一个独具特色的建筑物,对城市建筑美化起到积极影响。在实际的建筑施工之前,组合式建筑设计过程中,离不开组合式建筑的三维建模程序,而建模的效果与建筑物最终建筑效果之间存在直接联系。
组合式建筑每个部件之间存在很多的遮挡问题,针对此类建筑,建筑物建模方法在建模过程中,需要操作人员多次交互参与,操作流程复杂,导致组合式建筑几何轮廓数据拿捏不准,存在误差,为此,为了优化组合式建筑建模精度,协助设计人员准确地按照设计方案,实现组合式建筑最优设计,需要实现组合式建筑几何轮廓的定标误差识别,组合式建筑几何轮廓定标误差识别是优化组合式建筑物三维模型建模精度的基础和前提。本文设计一种组合式建筑几何轮廓定标误差识别模型,可高精度、快速识别组合式建筑几何轮廓定标误差。
2 组合式建筑几何轮廓定标误差识别模型
2.1 基于几何基元定标的组合式建筑模型轮廓数据提取方法
以常见的由长方体、圆柱体建立的组合式建筑为例,使用基于几何基元定标的组合式建筑模型轮廓数据提取方法,提取组合式建筑模型轮廓数据。
针对组合式建筑物而言,充分使用组合式建筑物每个部件的规则几何体具备的三维信息,将每个部件实施参数计算与建模,能够优化此类建筑物的建模速度与质量。针对差异的建筑物部件,使用差异的定标方法实现各个部件的轮廓参数计算和建模,能够全面提取差异几何体自身的轮廓特征。定标误差能够体现组合式建筑结构三维模型与实际建筑轮廓之间的建模误差,本文在识别组合式建筑几何轮廓定标误差之前,先以几何轮廓数据提取为研究核心,建立长方体几何基元定标模型、圆柱体几何基元定标模型,以此提取组合式建筑几何轮廓数据。
2.1.1 长方体几何基元定标模型
组合式建筑的三维建模过程中,长方体几何基元是组合式建筑建模的核心因素之一,所以构建一种长方体几何基元定标模型,提取组合式建筑的长方体结构几何轮廓数据。
在相机标定中,角点相应的三维坐标示意图见图1。

图1 角点相应的三维坐标示意图
为了实现相机标定,需要构建相机成像模型。相机成像模型能够描述组合式建筑结构三维模型中,某长方体几何轮廓坐标数据和实际轮廓坐标数据之间的映射关系。
相机标定时,需要运算相机内外参数与长方体结构轮廓的尺寸大小h
、h
,建模主要是为了使组合式建筑结构三维模型结构中长方体部件轮廓和组合式建筑的二维图像轮廓之间的匹配度满足应用需求。所以,使用常用的相机投影矩阵相机模型,构建相机成像模型N
=T
[S
|k
](1)
其中,相机内部矩阵是T
;旋转矩阵与平移向量依次是S
、k
,S
、k
属于相机外部矩阵。引入齐次坐标,投影矩阵将组合式建筑结构三维模型中各个长方体部件轮廓坐标数据Q
映射至相机所拍摄的组合式建筑物图像中二维点q
,便可计算获取相机内部参数、外部参数和尺寸大小。q
=NQ
(2)
通过映射关系q
↔Q
,采取动态线性规划的形式,获取相机标定的参数T
、S
、k
、h
、h
。相机标定完毕,便可使用式(2)运算获取世界坐标系中轮廓数点的坐标Q
。2.
1.
2 圆柱体几何基元定标模型在组合式建筑结构三维模型圆柱体几何结构中,为了实现相机标定,计算相机的内外参数,提取几何轮廓数据,需要引入透视投影的灭点理论的几何性质运算方法。
圆柱体灭点求解示意图见图2。

图2 圆柱体灭点求解示意图
图2中,u
、u
、u
是圆柱体灭点。设置灭点坐标为(v
,u
,1),v
、u
、1是灭点在x
轴、y
轴、z
轴上的轮廓数据。右上标T
代表转置。其对应的空间齐次坐标依次是(1,0,0,0),(0,1,0,0),(0,0,1,0)。此时相机内部参数和非已知、不等于0的因子λ
约束关系TS
是
(3)
因旋转矩阵属于正交矩阵,式(3)能够变换成

(4)
获取相机内部参数和不等于0的常数因子λ
之后,把参数导入式(4),便能获取旋转矩阵的值。求解相机标定参数后,根据灭点坐标便可判断组合式建筑中圆柱体部件的几何轮廓坐标参数(此参数主要是圆柱体部件的半径s
)。在世界坐标系中,操作人员标识的点坐标依次是(±s
,0,0)、(±s
,0,1),s
能够通过二维图像点至三维空间映射关系获取。综上所述,在提取组合式建筑几何轮廓数据之后,为了识别几何轮廓定标误差,本文将长方体部件、圆柱体部件的几何轮廓数据整理为组合式建筑不同部件的轮廓数据样本集合O
,作为基于支持向量回归机的几何轮廓定标误差识别方法的识别样本。2.2 基于支持向量回归机的几何轮廓定标误差识别方法
支持向量回归机能够使用敏感度为0的损失函数与核函数,具有显著的预测性能。所以,本文使用支持向量回归机对组合式建筑几何轮廓定标误差进行建模分析。
组合式建筑几何轮廓定标数据样本存在高维非线性属性,设置样本数据集为O
={(a
,b
),…,(a
,b
)},a
、b
是2.
1小节提取的组合式建筑不同部件的轮廓数据样本。为了把低维空间非线性回归问题变成高维空间的线性回归问题g
(a
),引入一个非线性映射系数φ
g
(a
)=ϖ·φ
+c
(5)
其中,c
、ϖ依次是阈值与权值。为了保证样本数据自低维空间非线性回归问题变成高维空间的线性回归结果g
(a
)与真实值存在极小的差异,需要将损失的实际风险值S
[g
]控制在最小值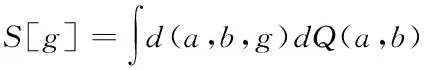
(6)
其中,d
代表求导处理。Q
(a
,b
)、d
(a
,b
,g
)分别是联合概率分布函数、损失函数。因为Q
(a
,b
)是未知的联合概率分布函数,不可以直接把S
[g
]实施最小化处理,所以,将其等价成最小化表达模式
(7)
其中,D
(ϖ)、D
依次是S
[g
]的最小化模式、惩罚参数。b
、g
(a
)依次是第j
个组合式建筑部件的轮廓数据样本数据、第j
个组合式建筑部件的轮廓数据样本数据自低维空间非线性回归问题变成高维空间的线性回归结果。求解式(5)时,可将式(6)等价成式(7)的最小化问题,则:

(8)
s.t.
((ϖ·φ
)+c
)-b
≤δ
+ε
(9)

(10)
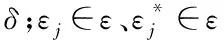
式(10)的对偶问题是


(11)
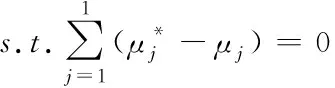
(12)

S
2的凸二次规划问题
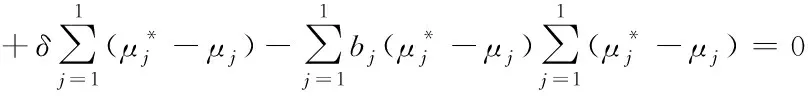
(13)


(14)


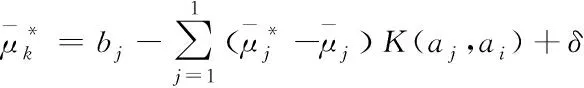
(15)
在支持向量回归机模型中,精度β
、惩罚参数D
、核函数参数的设置十分关键。因高斯径向基核函数的建模效率显著,建模误差极小,所以使用它设成几何轮廓定标误差识别的核函数。高斯径向基核函数是
(16)
其中,核函数的宽度向量是ψ
;a
∈a
、a
∈a
。基于支持向量回归的几何轮廓定标误差识别模型是
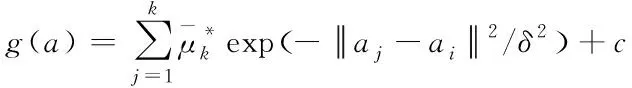
(17)
使用式(17)便可实现组合式建筑几何轮廓定标误差识别。
3 仿真结果与分析
实验在MATLAB仿真平台中,使用Emgucv和OpenGL库实现图3中2种组合式建筑物建模,实验中所研究的组合式建筑详情如图3所示。在建模过程中,将本文模型使用C#程序编写到应用程序中,主要使用本文模型提取2种组合式建筑物三维建模中的几何轮廓数据、识别定标误差,判断本文模型对组合式建筑物几何轮廓数据提取效果、定标误差识别效果以及操作效率。

图3 组合式建筑物
3.1 几何轮廓数据提取效果测试
为了判断本文模型对图3中两种组合式建筑物在三维建模过程中的几何轮廓数据提取效果,使用提取率W
、准确率W
2个指标进行评价。提取率能够描述本文模型提取的组合式建筑物三维建模中的轮廓数据量在实际建筑物轮廓数据量的比值,体现本文模型的提取全面性。准确率能够描述准确提取组合式建筑物三维建模中的轮廓数据量在所提取的轮廓数量的比值,体现本文模型提取的精度。
(18)
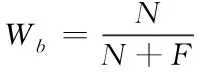
(19)
其中,N
是几何轮廓数据提取结果中实际建筑物轮廓数量;L
是没有被提取到的建筑物轮廓数量;F
是被错误提取成建筑物轮廓的数量。本文模型对A类组合式建筑物、B类组合式建筑物的几何轮廓数据提取效果如表1所示。

表1 几何轮廓数据提取效果
分析表1可知,本文模型对图3中两种组合式建筑物在三维建模过程中的几何轮廓数据提取效果较好,提取率都大于0.9800,提取准确率大于0.9900,可以全面、高精度地提取组合式建筑物三维模型中的几何轮廓数据。
3.2 几何轮廓定标误差识别效果测试
测试本文模型在识别图3中两种组合式建筑物三维建模时的几何轮廓定标误差时,识别结果的坐标平均误差值ρ,运算方法为
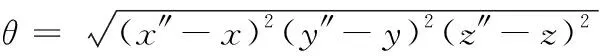
(20)
其中,x
、y
、z
表示组合式建筑物实际轮廓坐标。x
″、y
″、z
″是本文模型识别的轮廓坐标,坐标平均误差值较小,表示识别精度较高。测试结果如图4所示。
图4 几何轮廓定标误差识别效果
分析图4可知,本文模型在识别图3中两种组合式建筑物三维建模时的几何轮廓定标误差时,对两种组合式建筑物几何轮廓的定标误差识别精度较高,轮廓数据坐标平均误差值小于0.02,识别误差极小。
3.3 操作效率测试
测试本文模型提取2种组合式建筑物三维建模中的几何轮廓数据、识别定标误差时,所用的操作时长,以此判断本文模型的操作效率。测试结果如表2所示。
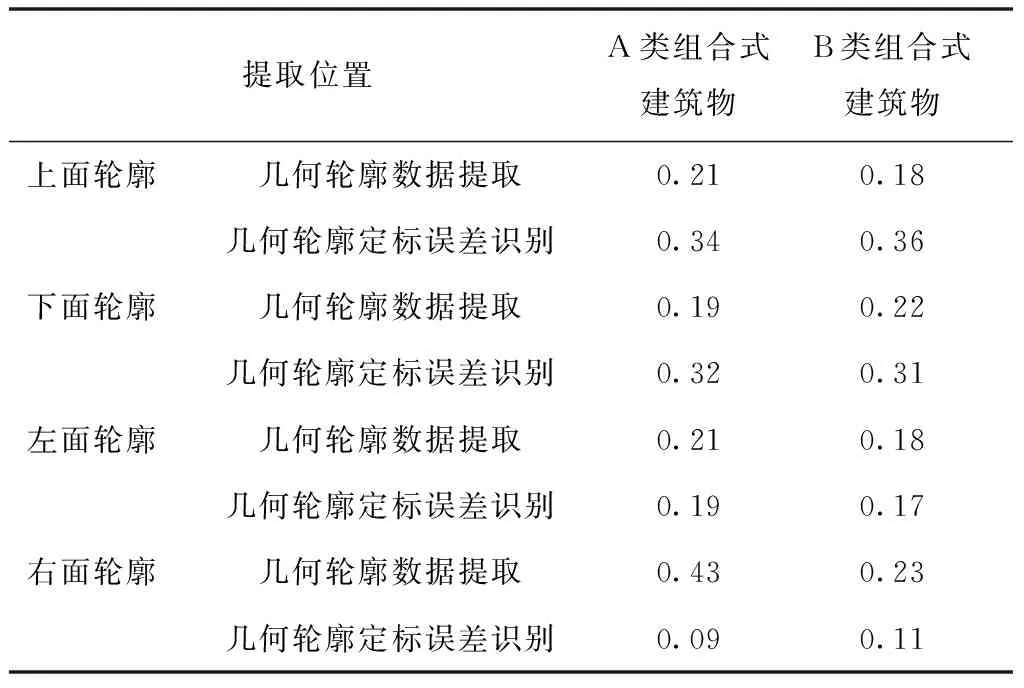
表2 操作效率测试结果
分析表2可知,本文模型提取2种组合式建筑物三维建模中的几何轮廓数据、识别定标误差时,操作时长较短,操作效率较高。
4 结论
建筑物的三维建模是虚拟现实与城市模拟仿真的核心构成部分,文章以优化组合式建筑三维建模精度为研究核心,设计了组合式建筑几何轮廓定标误差识别模型,该模型能够准确、全面提取组合式建筑模型轮廓数据;并实现几何轮廓定标误差高精度识别。但因篇幅有限,在提取组合式建筑几何轮廓数据时,仅以长方形、圆柱形建筑为例进行研究,在日后的研究中,将以其它形状的建筑轮廓为研究目标,提升本文模型的使用效果。
