建筑框架结构稳定性测试模型仿真分析
2022-07-20何悠,陈倩
何 悠,陈 倩
(1. 西南交通大学希望学院,四川 成都 610000;2. 西南财经大学天府学院,四川 成都 610000)
1 引言
建筑框架承受房屋所有荷载的结构,由许多的柱以及梁共同组成,然而,在高层民用建筑和多层工业建筑中,砖墙在大荷载条件下的承载力不能满足安全要求。因此,通常采用框架作为承重结构,房屋的荷载包括人的重量、货物的重量、房屋的重量、墙壁的重量、机器的重量以及地板和房屋本身的重量等。框架结构中的墙体仅起隔墙和围护作用,除自身重量外,不需要承受其它任何重量。因此,为了减轻框架的荷载,应采用轻质墙体,如浮石、膨胀珍珠岩、加气陶粒、空心砖或泡沫混凝土。
文献[1]根据现行规范抗震等级,引入三维退化虚层合单元,对两跨六层钢筋混凝土空间框架模型进行非线性有限元仿真分析。分析表明,板顶配筋对钢筋混凝土框架结构的侧向屈服机理影响最大,板底钢筋次之,板厚次之。分析了楼板参数对钢筋混凝土框架结构抗侧刚度和抗侧承载力的影响,结果表明,楼板参数对框架结构的抗侧刚度和抗侧承载力有明显的影响。文献[2]分析强震冲击下保持稳定的结构状态,通过圆柱分析法设计圆柱形支撑大跨度建筑结构强震下冲击分析仿真模型,完成模型的仿真分析与监测,提取稳定性较差建筑结构单元,明确圆柱形支撑大跨度建筑薄弱点,应用圆柱形支撑大跨度建筑结构,基于此对大跨度建筑结构强震冲击进行静力分析,达到提升圆柱形支撑大跨度建筑在强震冲击下稳定性的目的。文献[3]针对卫星用高稳定复合材料框架结构,采用Hyperworks有限元软件分析卫星本体和有效载荷过渡的框架结构在空间环境下的热变形状态,并对其构型进行了拓扑优化,分析复合材料框架重量,刚度和热稳定性的影响。
建筑物所承载的物体的性质和大小,土地和岩石的类型,甚至其在空间的分布、地下水的分布以及可能发生的地质灾害都是影响建筑物稳定性的因素,若是在施工设计过程中综合考虑上述因素,总结以往研究经验,做好预防对策或手段,那么建筑物稳定性将会得到有效提升。所以本文提出建筑框架结构稳定性测试模型,引入灵敏度分析法,创新性地对建筑框架稳定性全面考量,为建筑工程施工打下夯实基础。
2 建筑框架结构稳定性模型构建
2.1 整体稳定性分析
建筑框架层数结构和高宽比的增大、重力荷载的增大以及侧向刚度的缩小会在水平风向荷载与水平地震的作用下,具有P
-Δ
效应。而随着结构的水平位移增大,框架建筑竖向构件,会生成弹塑性的形变,使结构产生失稳,所以,建筑框架的结构稳定性受限,进行设计时,需要控制P
-Δ效应。
EJ
代表结构主轴方向弹性等效侧向的刚度,依据实际结构和等截面的悬臂杆,在倒三角的水平分布荷载作用下,顶部的位移相等进行求取。H
代表建筑的高度,G
代表第i
层重力荷载的设计值,n
代表结构总层数的计算。其中,EJ
能够间接反映出整体框架结构的稳定性。等截面的悬臂杆模型,在顶部加竖向力时的临界荷载,具体公式为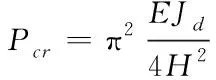
(1)

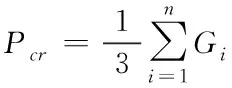
(2)
把式(1)代进式(2),可得出公式为

(3)
在考虑到P
-Δ效应的结构框架侧向位移Δ与不考虑P
-Δ效应结构框架的侧向位移Δ二者间的公式为
(4)
通过式(3)与式(4),能够推导得出侧向位移的增幅与刚重比二者之间的关系公式为
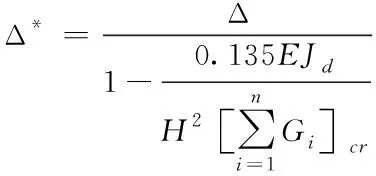
(5)
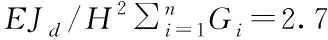
P
相关,同时和P
-Δ效应所引起的内力的限值l
与附加位移s
也相关,所以,建筑框架超规结构,一方面,要研究临界荷载,另一方面,还要考虑P
-Δ对于结构所附加的内力以及位移影响。2.2 临界荷载分析
高层建筑框架模型简化建筑结构如图1所示、计算坐标系如图2所示。

图1 模型简化示意图

图2 坐标系
将图1的模型简化,失稳过程挠曲线的函数公式为
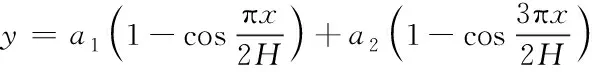
(6)
式中:a
,a
代表待定系数。则外力的势能公式为

(7)
式中,y
′表示势能一阶导数,x
表示失稳点坐标,d
表示调节系数,阶段外力势能的公式为
(8)

(9)

(10)
在互留加强的应变能力,即体系应变能公式为
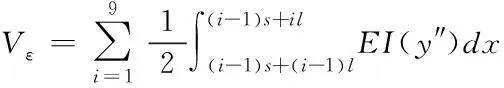
(11)
即总势能公式为

(12)
引入势能驻值原理,公式为
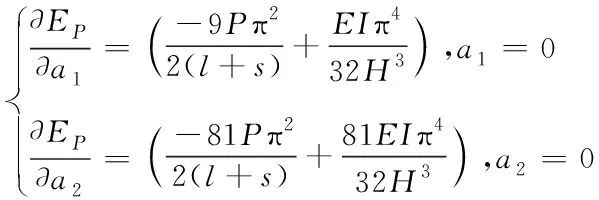
(13)
式中,由于待定系数a
,a
不全为零,因此公式求解为
(14)
在式(14)、(15)中,较小的识别参数P
值就是临界荷载,那么此模型临界荷载的公式为
(15)
2.3 二阶效应
增大系数法是一种简单的可行考虑P
-Δ效应方法。此类方法不需要进行P
-Δ效应复杂的分析,将不考虑P
-Δ效应结构的侧向位移与增大系数相乘,得出近似P
-Δ效应的影响值。考虑到P
-Δ效应结构侧向位移Δ与不考虑P
-Δ效应结构侧向位移Δ二者之间关系,因此,将(Δ-Δ)/
Δ值作为P
-Δ效应评判的标准。3 简化模型参数识别
为了使修正具有针对性,在模型修正过程中,采用灵敏度分析方法,选择的修正参数是质量密度、截面几何特性以及弹性膜量等物流参数。利用有限元法代表无阻尼的自由振动特征方程,公式为
(K
-λ
M
)φ
=0 (i
=1,2,…,m
)(16)
式中:M
表示结构框架的特征值,λ
表示第一特征向量,M
为框架结构的质量矩阵,K
表示和刚度矩阵,代表质量矩阵以及框架结构刚度矩阵,结构框架的第i
阶特征向量以及特征值,通过p
的Taylor
计数形式展开,具体公式为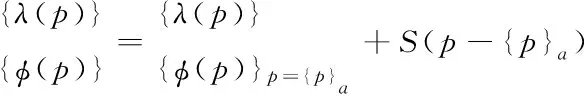
(17)
式中:{p
}代表识别参数p
在没有修正时起始值,S
代表灵敏的矩阵。可以将其改写成
(18)
使s
≠n
代表已知的测试特征,对于构成灵敏度的矩阵行数,就是式(18)内的方程数目。在给定m
阶特征的测点频率以及n
测点的k
阶振型后,由于阶数的频率信息和不同的振型,则n
=m
+n
×k
,且k
与m
之相同。为方便叙述,认为特征值与特征向量的阶数相同,而在未知参数的数目s
≠n
时,式(18)有唯一的解。具体如下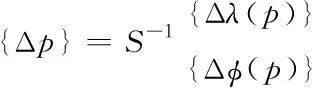
(19)
在s
≠n
时,按照最小的二乘准则,上式内的S
应该是S
广义逆S
(SS
)。通过解析计算,可以利用灵敏度矩阵特征导数来识别结构的弹性模量,即在得到灵敏度矩阵后,根据其数值计算得到建筑结构的弹性模量。
频率或振型数据可按上述方法计算,但是,如果在计算中,同时识别这两类数据,由于两类数据的级别不匹配,某类数据在识别过程中有可能占据优势,因此,为了得到相应的频率和模式变化值,避免灵敏度矩阵病态化,利用下式所构建的灵敏度矩阵第j
列,公式为φ
(E
)=∂φ
/φ
(20)
将式(21)替换成

(21)
即可完成建筑模型的稳定性参数识别。
4 实验分析
选取某公司生产的风冷系列电动振动试验系统,其正弦激振力范围为1kN~70kN,随机与正弦激振力比为1:1,存在两倍的正弦冲击力,位移峰峰值40 mm,设其中心室的空气弹簧承载可调,在振动台上输入相同的地震波激励,分别对无阻尼器和有阻尼器的振动台进行试验研究,与此同时,在相同地震波激励下,观察两种模型的不同地震响应。由于振动台的局限性,这两种模型不可能同时进行试验。因此,测试是按顺序进行的,但是输入振动台的加速度是相同的。
4.1 模型的动力特性
试验的主要目的是观察模型的动态变化,而白噪声输入结构响应是一种特殊的状态响应,所以以微幅振动响应为验证指标,测试每个实验的相频。理论上白噪声输入结构进入弹塑性状态后,没有固定的频率,但仍可以微幅振动响应推导出结构的等效刚度退化程度如图3所示,其中的虚线和实线分别为阻尼器的模型和无阻尼器的模型自振频率退化测试结果。
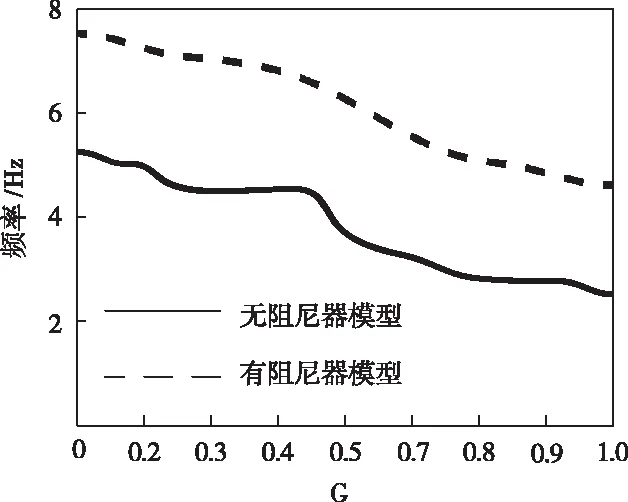
图3 模型自振的频率退化图像
由图3可知,在频率退化验证结果中,无阻尼器结构的刚度退化率高于有阻尼器的结构,而有粘滞阻尼器的结构刚度退化速度较慢。当结构进入弹塑性阶段时,结构的地震反应会降低。从图3的结果可以看出,无阻尼器结构的刚度退化率高于有阻尼器的结构。无阻尼器结构,8度设防后,一阶振型频率降低20%;有阻尼器结构,8度设防后,一阶振型频率仅降低15%;在罕遇地震和8级罕遇地震后,阻尼结构的一阶振型频率降低了32.4%,而无阻尼器结构的一阶振型频率降低58.9%。
4.2 分析位移反映
测试两种结构模型模型层间位移随着加速度的变化情况以及绝对的位移反映结果,如图4、图5所示。

图4 模型水平最大的位移

图5 模型层间的位移输入变化图像
从图3和图4可以看出,设置粘滞阻尼器的模型位移响应降低了37%,8度设防组的位移响应降低了66%,罕遇地震组的位移响应降低了66%。
由图5中可知,当两个模型的薄弱层相对位移相同时,位移比较结果在有阻尼器模型的输入加速度的情况下约为无阻尼器模型的1.5倍。在0.4g时,两种模型产生的第一条裂纹的产生时间非常接近。最终试验后,无阻尼结构产生不可恢复的变形。
4.3 应变分析
测试内模型框的柱端、架梁部位埋设钢筋应变片,对比模型的构件在每个工况之间应变绝对值,如表1、2所示:
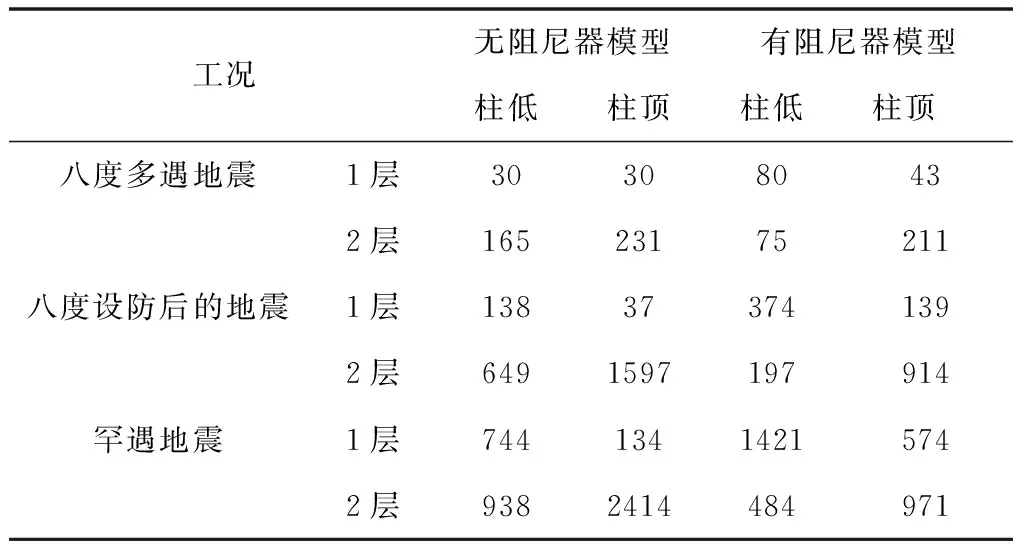
表1 模型框架柱的应变绝对值对比
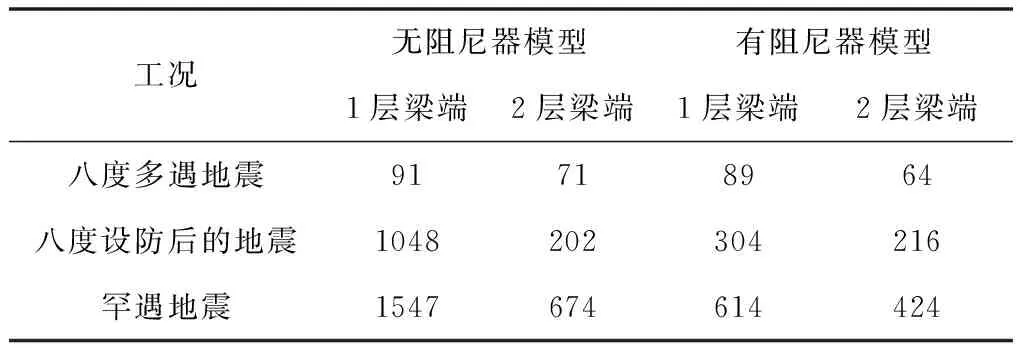
表2 模型框架梁应变的绝对值对比
通过表1、2能够看出,在罕见地震作用下,2层框架和1层框架的弯矩明显减小,而采用减振器模型的构件的钢筋应变减小,只有1层框架柱的应变增大。
5 结束语
1)通过分析建筑物框架稳定性可知,在八度设防后,第一振型频率仅降低15%,8级罕遇地震后,无阻尼器结构的第一阶振型频率降低了58.9%,而在8级罕遇地震中,阻尼结构的第一阶振型频率降低了32.4%,即阻尼器结构可在地震测试下降低结构破损情况。
2)通过分析框架节点的弯矩平衡可知,第一层框架柱因轴力变化而降低弯矩,增加了钢筋的应变。
3)该方法虽然能够很好模拟建筑物的结构稳定性情况,但是由于模拟的过程仍较为繁琐,所以未来研究要向着更精确、更快速识别的方向优化。
