车辆状态与参数联合估计研究

姬 晓，李 刚，2，樊东升

(1. 辽宁工业大学汽车与交通工程学院，辽宁 锦州 121001；2. 吉林大学汽车仿真与控制国家重点实验室，吉林 长春 130025)

1 引言

在当今社会所倡导的低碳与零排放发展趋势下，推广电动汽车取代传统燃油车已经成为近几年汽车行业转型的有效手段之一。而分布式驱动电动汽车又作为电动汽车重要发展方向之一，为汽车在主动安全控制及稳定性控制等方面带来了显著的优势。汽车关键状态与参数变量的准确获取是进行车辆主动安全控制以及稳定性控制的前提。但针对这些重要参数变量的估计研究普遍采用算法模型估计器，算法模型中车辆自身的一些参数(如质量、转动惯量和质心位置等)以及路面附着系数通常直接采用固定值，在对车辆行驶状态估计的过程中大多忽略这些参数变化的影响。此外在汽车行驶的过程中，由于工况的不断变化，导致这些参数变量也随之不断发生改变，从而影响汽车行驶状态估计的准确性。因此，在车辆行驶状态估计的过程中同时考虑车辆自身参数以及路面附着系数的变化就显得尤为重要。文献[4]采用单一扩展卡尔曼滤波理论的状态与参数估计框架，实现了对车辆运动状态的实时估计，但未实现对其它参数的估计。文献[5]将单轮胎滑移控制模型与扩展卡尔曼滤波器结合估计车辆的运动状态、路面附着系数、车轮滑移率和质量参数，但无法使用足够的信息来计算协方差矩阵，有待调整和改善。文献[6]基于改进的Sage-Husa自适应扩展卡尔曼滤波理论对车辆的行驶状态进行估计，提高了算法的鲁棒性。文献[7]考虑路面附着系数的影响，将平方根容积卡尔曼滤波算法与多模型交互算法进行融合，提高了车辆状态参数估计的跟踪精度。文献[8]针对多轴分布式电驱动车辆，通过建立双重无迹卡尔曼滤波器(DUKF)对车辆状态和车辆参数进行联合估计。文献[9]基于三容积卡尔曼滤波理论设计了车辆状态与参数联合估计算法，通过三个估计器间信息的相互校正，进一步提高了算法的准确性。

针对普通算法的估计精度不高及实时性不好，容积卡尔曼滤波因系统模型不准确可能出现结果发散等问题。本文提出一种联邦-容积卡尔曼滤波方法，联邦卡尔曼滤波是从分散化滤波的基础上逐渐发展而来的，具有设计灵活、容错性好的特点，这种相结合的方式充分利用了各自的优点，可以使过程噪声在估计过程中自适应变化，具有较高的估计精度和良好的容错性以及稳定性。论文选取融合重置结构对两个子滤波器和一个主滤波器进行设计，并对每一个子滤波器中的时间更新和测量更新采用容积卡尔曼滤波算法，最后通过实验对该法进行了验证。

2 车辆估计模型

2.1 分布式驱动电动汽车车辆动力学模型

车辆动力学模型表征着汽车在运动过程中不同参数变量之间的数学关系，是设计车辆状态与参数估计算法的基础。针对分布式驱动电动汽车，考虑到整个估计算法的时效性以及纵向、侧向和横摆三个方面的运动，依据传统二自由度模型建模方法，并在此基础上进行相应假设建立三自由度车辆估计模型。模型进行假设如下：

1)坐标原点与质心重合。

2)假设车辆由一个刚性车体和四个相互独立控制的车轮构成。

3)假设各轮胎机械特性相同。

4)忽略悬架系统作用。

车辆模型如图1所示。

图1 车辆动力学估计模型

图1中：

a

和

b

分别为质心至前、后轴的距离，

t

和

t

分别为前、后轮轮距，

v

为车轮中心速度，

δ

为通过转向电机直接获取的四轮转角，

F

＿为轮胎纵向力，

F

＿为轮胎侧向力，

α

为轮胎侧偏角。其中，

i

代表前轮或者后轮，

j

代表左轮或右轮。

车辆动力学模型方程如(1)、(2)、(3)所示

(1)

(2)

(3)

式中：

v

和

u

分别为纵

/

侧向车速，

a

和

a

分别为纵

/

侧向加速度，

r

为横摆角速度，

I

为汽车绕

z

轴的转动惯量，Г为横摆力矩。由动力学模型计算

a

、

a

和Г公式如式(4)、(5)、(6)所示

+

F

＿cos

δ

+

F

＿sin

δ

+

F

＿cos

δ

+

F

＿sin

δ

)

(4)

-

F

＿cos

δ

+

F

＿sin

δ

-

F

＿cos

δ

+

F

＿sin

δ

) (5)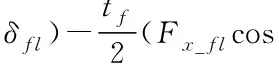

(6)

式中，四轮的侧偏角、线速度和法向反作用力计算公式如式(7)、(8)、(9)所示

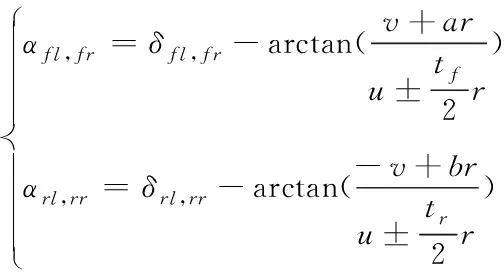
(7)

{

v

，=(

u

±

t

2

r

)+(

v

+

ar

)

v

，=(

u

±

t

2

r

)+(

v

-

br

)

(8)

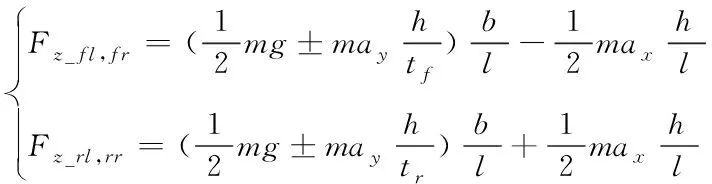
(9)

式中：

F

＿为地面对车轮的法向反力，

m

为整车质量，

l

为轴距，

h

为质心高度。

四轮纵向力可通过式(10)进行计算

(10)

2.2 侧向力计算

采用Dugoff 轮胎模型计算四轮的侧向力，公式如式(11)所示

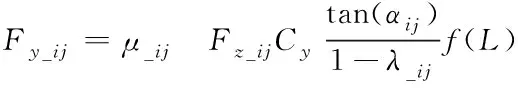
(11)

式中：

μ

＿为路面附着系数，

C

为轮胎侧偏刚度，

λ

＿为纵向滑移率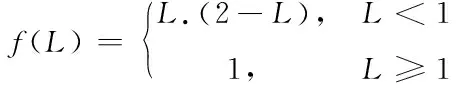

(12)

(13)

式中：

C

为轮胎纵向刚度，

ε

为速度影响因子。

制动和驱动对应的滑移率公式如式(14)所示

(14)

3 车辆状态与参数联合估计算法设计

3.1 联合估计原理

分布式驱动电动汽车状态与参数联合估计原理示意图如图2所示。首先通过整车通讯网络采集车载传感器信号，主要包括车辆的纵向加速度、侧向加速度、横摆角速度、四轮转角、四轮转速和四轮驱动力矩。将这些传感器信号同时传输给行驶状态估计器、附着系数估计器和车辆参数估计器中各主

/

子滤波器以及Dugoff轮胎模型作为算法模型的信号输入。经过轮胎模型解算出轮胎侧向力，通过轮胎纵向力计算模块将采集到的四轮驱动力矩直接换算成四轮所受的纵向力，以减小轮胎模型本身对计算轮胎力所产生的误差。将所得到的轮胎力又作为各个估计器中各主/子滤波器的另一个输入。与上一章的联合估计算法所不同的是算法模型中的车辆自身参数不再设定为固定值，而是接收来自算法估计器实时估计得到的修正值。三个联合估计器中的主滤波器在接收到这些信号后进行初始化，信息分配系数默认值为零，将车辆参数变量、行驶状态变量、附着系数变量、协方差矩阵和过程噪声矩阵相应分配给各子滤波器，每一个子滤波器对所接收到的传感器信号和分配后的信号进行整合，首先完成时间更新得到先验状态估计值，再根据各自的测量值完成测量更新得到后验局部估计值，再将这些数据一同传递给主滤波器进行整合完成全局最优估计。最优估计值作为输出的同时又按照特定的分配原则再次对各子滤波器进行信息分配，从而完成一次迭代，随着时间不断迭代在三个估计器中各自形成闭环。同时全局最优车辆参数估计值又反馈给行驶状态估计器、路面附着系数估计器与轮胎模型，全局最优行驶状态估计值又反馈给路面附着系数估计器、车辆参数估计器与轮胎模型，全局最优路面附着系数估计值又反馈给行驶状态估计器、车辆参数估计器与轮胎模型。车辆状态与参数进行实时修正并及时反馈，不仅在每个估计器内部形成闭环系统，整个系统在三个估计器外也形成闭环，由此完成对车辆状态与参数的准确估计。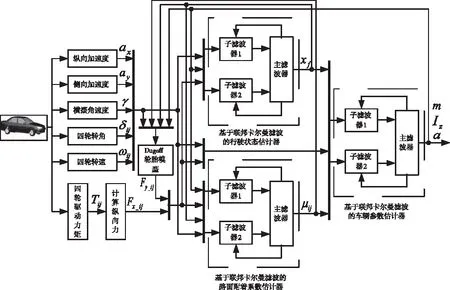

图2 联合估计原理图

3.2 联合估计算法

联合估计算法具体设计过程如式(15)～(71)所示。

1)车辆自身参数的信息分配过程

首先通过主滤波器将车辆自身参数变量、误差协方差矩阵与系统过程噪声协方差矩阵，按照信息分配的原则分配给每一个子滤波器。

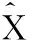
(15)

(16)

(17)

式中：

β

为车辆自身参数信息分配系数，其中

i

=1，2(即两个子滤波器)，根据信息守恒有

β

+

β

2=1。

2)车辆行驶状态的信息分配过程

首先通过主滤波器将行驶状态变量、误差协方差矩阵与系统过程噪声协方差矩阵，按照信息分配的原则分配给每一个子滤波器。

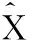
(18)

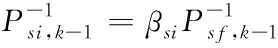
(19)

(20)

式中：

β

为行驶状态信息分配系数，其中

i

=1，2(即两个子滤波器)，根据信息守恒原则有

β

+

β

2=1。

3)路面附着系数的信息分配过程

通过主滤波器将路面附着系数参数变量、误差协方差矩阵与系统过程噪声协方差矩阵，按照信息分配的原则分配给每一个子滤波器。

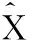
(21)

(22)

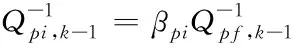
(23)

式中：

β

为路面附着系数信息分配系数，其中

i

=1，2(即两个子滤波器)，并根据信息守恒原则有

β

+

β

2=1。

4)车辆自身参数的时间更新过程

在每一个车辆自身参数子滤波器中单独进行时间更新。

①采用SVD法将协方差矩阵

P

，-1进行分解

(24)

②计算前一时刻的容积点

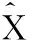
(25)

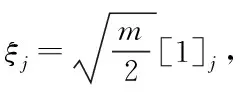
③计算系统方程迭代后的容积点

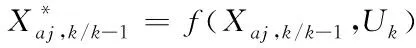
(26)

④估计经过时间更新后的状态预测值

(27)

⑤估计误差协方差矩阵的预测值

(28)

式中：

Q

为车辆参数过程噪声协方差矩阵。

5)车辆行驶状态的时间更新

在每一个行驶状态子滤波器中独立进行时间更新。

①采用SVD法对协方差矩阵

P

，-1进行分解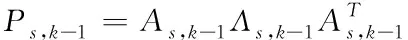

(29)

式中：

A

，-1为行驶状态协方差矩阵

P

，-1所对应的特征矩阵。

②计算前一时刻的容积点：

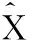
(30)

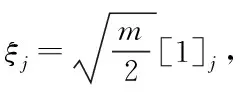
③计算系统方程迭代后的容积点

(31)

④估计经过时间更新后的状态预测值

(32)

⑤估计误差协方差矩阵的预测值

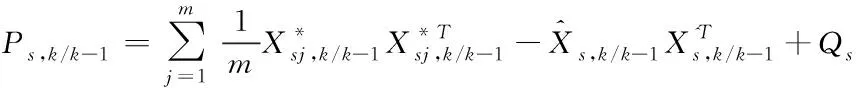
(33)

式中：

Q

为行驶状态过程噪声协方差矩阵。

6)路面附着系数的时间更新

在每一个路面附着系数子滤波器中独立进行时间更新。

①采用

SVD

法对协方差矩阵

P

，-1进行分解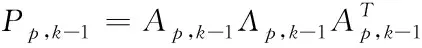

(34)

式中：

A

，-1为路面附着系数协方差矩阵

P

，-1所对应的特征矩阵。

②计算前一时刻的容积点：

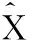
(35)

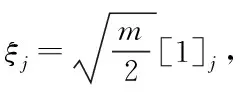
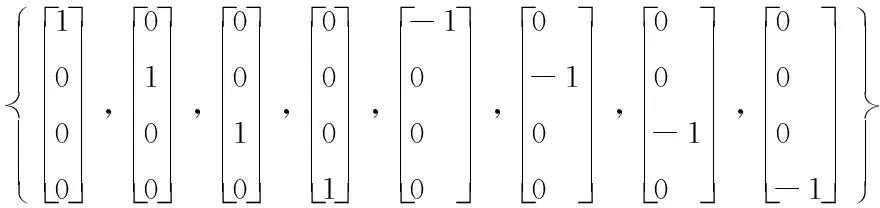
③计算经过转移方程迭代后的容积点

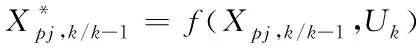
(36)

④估计经过时间更新后的预测值：

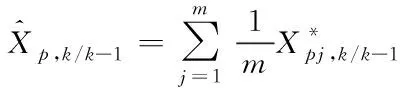
(37)

⑤估计误差协方差矩阵的预测值

(38)

式中：

Q

为路面附着系数过程噪声协方差矩阵。

7)车辆自身参数的测量更新过程

在每一个车辆自身参数子滤波器中单独进行测量更新。

①采用

SVD

法将预测的协方差矩阵

P

，-1进行分解：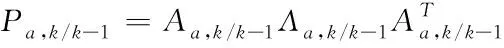

(39)

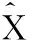
(40)

③根据测量变量计算新的容积点：

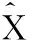
(41)

④对容积点求均值

(42)

⑤计算新息方差

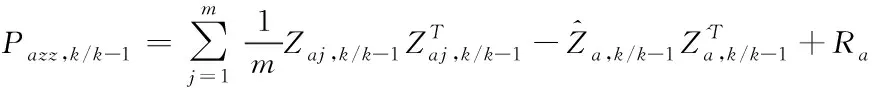
(43)

式中：

R

为车辆自身参数测量噪声协方差矩阵。

⑥计算互协方差

(44)

⑦计算滤波增益

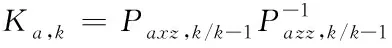
(45)

⑧经过测量变量校正后的状态估计：

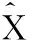
(46)

⑨校正误差协方差矩阵：

(47)

8)车辆行驶状态的测量更新过程

在每一个行驶状态子滤波器中单独进行测量更新。

①采用SVD法将预测的协方差矩阵

P

，-1进行分解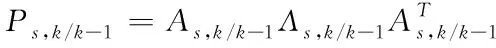

(48)

②计算容积点

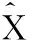
(49)

③根据测量变量计算新的容积点

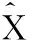
(50)

④对容积点求均值

(51)

⑤计算新息方差

(52)

式中：

R

为行驶状态测量噪声协方差矩阵。

⑥计算互协方差

(53)

⑦计算滤波增益

(54)

⑧经过测量变量校正后的状态估计

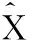
(55)

⑨校正误差协方差矩阵：

(56)

9)路面附着系数的测量更新过程

在每一个路面附着系数子滤波器中单独进行测量更新。

①采用SVD法将预测的协方差矩阵

P

，-1进行分解

(57)

②计算容积点

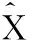
(58)

③根据测量变量计算新的容积点

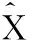
(59)

④对容积点求均值

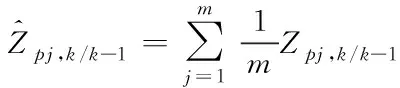
(60)

⑤计算新息方差

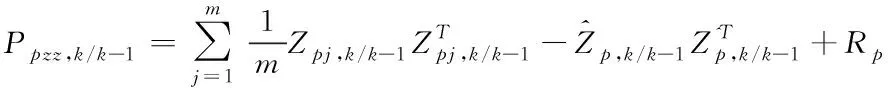
(61)

式中：

R

为路面附着系数测量噪声协方差矩阵。

⑥计算互协方差

(62)

⑦计算滤波增益

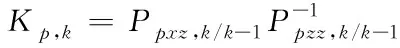
(63)

⑧经过测量变量校正后的状态估计

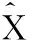
(64)

⑨校正误差协方差矩阵

(65)

10)车辆自身参数的信息融合过程

对车辆自身参数中各子滤波器的局部估计值通过主滤波器进行融合得到全局最优估计。

(66)

(67)

11)车辆行驶状态的信息融合过程

对车辆行驶状态中各子滤波器的局部估计值通过主滤波器进行融合得到全局

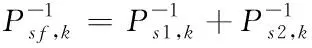
(68)

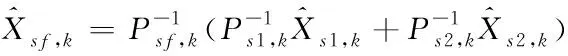
(69)

12)路面附着系数的信息融合过程

对路面附着系数中各子滤波器的局部估计值通过主滤波器进行融合得到全局最优估计

(70)

(71)

建立非线性系统的状态与量测方程并给出各变量所含参数，公式如式(72)所示：

X

，=

f

(

X

，-1，

U

，-1，

W

，-1)

Z

，=

h

(

X

，，

v

，)

(72)

车辆自身参数估计器中两个子滤波器的状态变量为：

X

，=[

m

，

I

，

a

]。行驶状态估计器和附着系数估计器中两个子滤波器的状态变量分别为：

X

，=[

u

，

v

，

a

，

a

，

γ

，

Γ

]，

X

=[

μ

，

μ

，

μ

，

μ

]。

行驶状态估计器中子滤波器1，2的测量变量分别为：

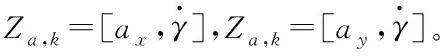
Z

，=[

a

，

a

，

γ

]，

Z

，=[

a

，

γ

]。

控制输入量为：

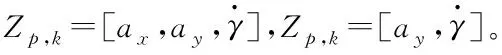
U

，=[

δ

，

δ

，

δ

，

δ

，

ω

，

ω

，

ω

，

ω

]。其中：

δ

为四轮转角，是通过传感器采集方向盘转角信号按照一定规则计算所得到的。

信息分配系数的确定是联邦滤波器设计中的关键问题，合理的选取主滤波器和子滤波器之间的信息分配系数可有效改善子滤波器的算法估计精度和故障检测灵敏度，从而保证全局估计的最优性。鉴于协方差矩阵能够极大程度上反映各子滤波器的估计精度，因此将其作为衡量的指标计算信息分配系数。本论文采用式(73)的方式进行分配。

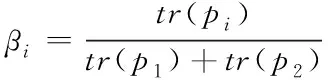
(73)

式中：

tr

(

p

)为误差协方差矩阵的迹，并设定信息分配系数的初值

β

=

β

=0。

4 仿真验证

为验证所提出的估计算法的可行性和可靠性，在Matlab/Simulink环境下搭建相应的算法模型，同时与CarSim进行联合仿真，评估估计算法对车辆非线性行驶状态的估计效果。设置相应试验工况，选择低附着蛇形实验工况。车辆模型部分参数如表1所示。

表1 车辆模型的部分参数

此工况的参数设置如下：车速为恒定值20km/h，附着系数设为0.2，采样步长为0.02s。行驶状态估计器中两个子滤波器初值选取

X

1,0=[20

/

3

.

6,0,0,0,0,0]

P

1,0=

eye

(6)

Q

1,0=

eye

(6)

R

10=

diag

([0

.

0,1,15])*0

.

1

X

2,0=[20

/

3

.

6,0,0,0,0,0]

P

2,0=

eye

(6)

Q

2,0=

eye

(6)

R

20=

diag

([0

.

0,1])*0

.

01

路面附着系数估计器中两个子滤波初值选取

X

1,0=[1,1,1,1]

P

1,0=

eye

(4)*2

Q

1,0=

eye

(4)

R

10=

eye

(3)*1000

X

2,0=[1,1,1,1]

P

2,0=

eye

(4)*2

Q

2,0=

eye

(4)

R

20=

eye

(2)*100

车辆参数估计器中两个子滤波器初值选取

X

1,0=[700,1400,1]

P

1,0=

eye

(3)*100

Q

1,0=

eye

(3)*0

.

001

R

10=

eye

(2)*1000

X

2,0=[700,1400,1]

P

2,0=

eye

(3)*10

Q

2,0=

eye

(3)*0

.

1

R

20=

eye

(2)*10

仿真结果如图3和图4所示，其中图3是CarSim仿真结果输出的传感器信号，即通过整车网络采集的车载传感器信号。图4中的(a)、(b)、(c)、(d)、(e)、(f)和(g)为联邦-容积卡尔曼滤波理论估计得到的车辆状态与参数估计值与相应状态参数实际值之间的对比结果。图4(a)为纵向车速估计值与整车仿真模型输出的实际值之间的对比曲线，从图中曲线可以看出在仿真开始后，估计值与实际值保持良好的一致性，即使速度处于峰值时，两者之间的误差也非常小。图4(b)为侧向车速的估计值与实际值之间的对比曲线，图4(c)为质心侧偏角的估计值与实际值之间的对比曲线，估计值与实际值基本相吻合，在估计准确性、稳定性和实时性方面表现良好。图4(d)为附着系数估计值与实验工况所设定的实际值之间的对比曲线，在仿真初始时刻估计值就开始立即收敛到真实值处，待达到真实值附近开始处于稳定，在精度和稳定性方面表现良好。图4(e)为质量的估计值与整车模型参数的设定值之间的对比曲线，图4(f)为转动惯量估计值与整车模型参数的设定值之间的对比曲线，图4(g)为质心位置的估计值与整车模型参数的设定值之间的对比曲线，在仿真开始后估计值产生一些波动后都能迅速收敛到真实值处并保持稳定。综上所述，估计算法在精度、实时性与稳定性方面都表现出良好的效果。

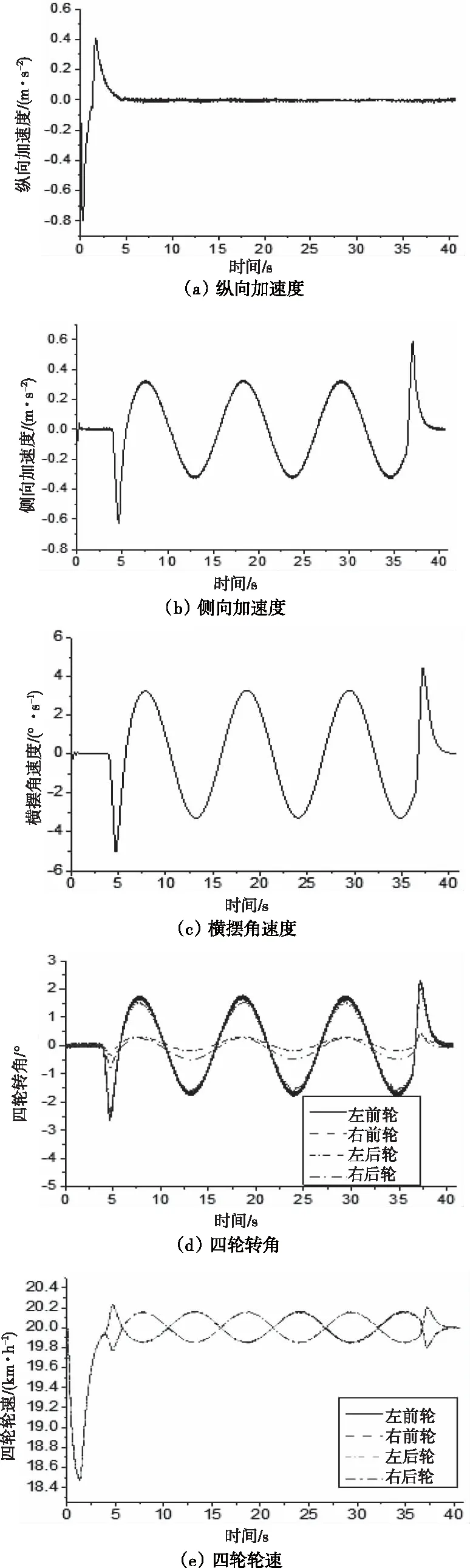
图3 传感器信号

图4 车辆行驶状态与路面附着系数仿真输出

5 结论

1)研究了一种联邦-容积卡尔曼滤波方法对分布式驱动电动汽车的状态与参数进行联合估计，并采用两个子滤波器和一个主滤波器的设计方式，其中子滤波器基于容积卡尔曼滤波理论进行设计，使过程噪声在估计过程中自适应变化，提高了整个算法的估计精度。

2)运用Matlab/Simulink模块化编程软件对联合估计算法模型进行搭建，并结合CarSim仿真平台对算法进行实验验证，结果表明：该算法显著提高了估计精度和稳定性、鲁棒性好。