基于单步预测LSTM的短期负荷预测模型

李 鑫，李海明，马 健

(上海电力大学计算机科学与技术学院，上海 200000)

1 引言

负荷预测是智能电网发展过程中的一项重要任务。负荷预测值过高，会造成电力系统能源的浪费；相反，预测值过低，将给电力系统带来诸多问题，比如降低系统可靠性，使电能质量下降等。准确的负荷预测对于电力系统调度和安全、可靠、经济的系统运行至关重要。现如今随着可再生能源并入电网、电动汽车的日益普及和配电网负荷需求的时变性，不可避免地增加了系统的复杂性、不确定性和负荷序列的非平稳性，使负荷的准确预测变得更为困难。

在负荷数据预处理阶段，文献[2][3]对缺失值采用取均值，插值法等，表面上是填充了缺失值，但实际上相当于间接引入了误差；对异常值直接舍去，可能会忽略某些重要因素，存在一定缺陷。如今智能电表基础设施(SMI)在国内的不断发展和广泛普及，为推动传统电力系统向智能电网发展奠定了基础。这种大规模部署所获取的负荷相关数据较为完善，存在较少的缺失异常值。在此基础上，文中未对缺失异常值直接进行处理，而是在数据归一化阶段解决了这方面的问题。在特征提取方面，文献[2][4]采用person相关系数分析对电力负荷进行特征选择。但由于电力系统相关数据是多维非线性的。采用线性相关的Pearson系数分析并不合适。

电力负荷预测模型主要有传统模型和人工智能模型。近些年来，人工智能模型由于对非线性序列具有良好的预测能力，从而广泛应用于电力系统负荷预测中。人工智能预测算法主要有支持向量回归(SVR)、多层感知机(MLP)、深度学习以及集成预测。文献[5]考虑了负荷及气象因素多种特征，并采用PSO-SVM预测模型。 结果表明，PSO-SVM具有较好的泛化能力，但随着输入特征维度增加，SVM预测模型训练时间变长，精度有所下降。文献[6]采用灰色系统与神经网络组合搭建预测模型，有效的提高了预测精度。但神经网络易于陷入局部最优解，存在收敛速度慢的缺点。文献[7]提出了一种基于深度信念网络(DBN)的短期负荷方法，结果表明此方法能够较好处理高维、复杂非线性数据，但DBN在计算过程中存在着训练时间较长、容易过拟合的缺点。基于小波神经网络(WNN)的预测模型将天气预报变量以及历史负荷数据作为输入特征。在文献[9]中提出了使用温度预测数据作为预测因子。由于电气负荷与天气部分相关，因此合理准确的天气预报可以显着提高预测准确性。基于天气预报的模型需要可靠的互联网连接，这在大容量电力系统中通常非常可靠。

极限学习机(ELM)是一个前向传播的神经网络，相对于 传统神经网络，其最大的特点在于再保证一定学习精度的前提下，能够较少一半的运算量，使学习速度更快。广义回归神经网络(GRNN)是径向基神经网络(RBF)的一种。GRNN是利用密度函数来预测输出，具有很强的非线性映射能力，而且收敛速度快。但是，由于GRNN中每个测试数据需要与全部训练数据进行计算，因此计算复杂度高。而且因为没有模型参数，需要存储全部的训练数据，这就导致空间复杂度增加。

因此，为提高负荷预测精度，本文提出提出一种单步负荷预测的双层LSTM模型。首先，采用最大信息系数(MIC)对多源异构特征进行选择。随机森林和递归特征消除(RFE)进行特征选择。在预处理过程中采用对含异常值敏感的Robust标准化方法进行处理。最后预测模型采用单步预测的双层LSTM层训练深度学习网络，并得出最终预测结果。与其它基准预测模型做对比，结果表明本文方法具有更高预测精度。在可预测的能源管理应用中，尤其是在负荷分布更加不稳定的小型微电网中，可以采用3步和24步范围。最后，在ELM，GRNN和LSTM算法中建立实验模型，以评估LSTM模型的性能。

2 特征准备与选择

2.1 数据准备

本文以美国德州西部地区的总荷载为基准。来自同一地区不同本地数据中心的每小时天气数据是从国家可再生能源实验室(NREL)网站收集的2012-2015年期间的数据。

2.2 数据提取

最大信息系数MIC是2011年由David N. Reshef发表在《Science》上的一篇文章中提出的。它是在互信息(MI)的基础上发展而来，互信息用来衡量变量之间的非线性依赖程度。设

X

，

Y

为随机变量，则互信息定义为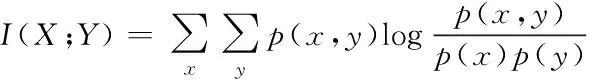

(1)

其中，

p

(

x

，

y

)为联合概率密度函数，

p

(

x

)和

p

(

y

)为边缘密度函数。两个变量之间互信息越大，则相关性越强。而

MIC

克服了互信息对连续变量计算不便的缺点，当拥有足够的统计样本时可以捕获广泛的关系，更能体现属性之间的关联程度。

MIC

计算主要分为三步：

2)对最大互信息值进行归一化处理，将互信息值转化到(0，1)区间；

3)选择不同网格尺度下互信息的最大值作为最终

MIC

值。

MIC

的整体求值公式为

(2)

式中：|

X

|*|

Y

|<

B

表示网格划分总数约束条件， 一般小于

B

(

B

为数据总量的0

.

6次方)。 不同网格尺度即为给定多种(

m

，

n

)值来进行网格划分。

MIC

是一种归一化的最大互信息，具有比互信息更高的准确度。两个变量之间

MIC

值越大，则其相关性越强；相反，则相关性越弱。文中依据最大信息系数(

MIC

)选出相关性强的特征作为预测模型输入。输入的总体特征

F

为

F

=[

A

，

Q

1，

Q

2，…，

D

1，

D

2，…]

(3)

其中，

A

为待预测负荷所属日类型，定义

A

=1为工作日，

A

=0为周末或假日；

Q

1，

Q

2，… 表示经

MIC

特征选择后的气象特征变量，

D

1，

D

2，… 表示日期类型特征变量，下标

i

为对应负荷时刻的气象和日期类型变量，

i

=1，2，3…

.n

，

n

为输入负荷值个数。数据提取结果如图1。

图1 MIC特征(属性)提取

2.3 数据选择

随机森林是机器学习中的算法之一。它根据特征的重要性来选择特征。使用每个决策树中的节点杂质来计算特征的重要性。随机森林中，最终的特征重要性是所有决策树特征重要性的平均值。而递归特征消除(Recursive Feature Elimination)，简称RFE。针对哪些特征含有权重的预测模型，RFE通过递归的方式，不断减少特征集的规模来选择需要的特征。通过选择性能最差或最好的功能来反复构建任何模型。RFE计算等级和维度，并仅基于等级和维度保留最重要的功能。特征重要性如图2。

图2 随机森林特征重要性

选择前6个与负荷相关性强的属性，并依据对应的权重值作为预测模型的输入。

2.4 数据预处理

负荷数据预处理主要包括缺失异常值处理和归一化。如将缺失异常值舍去或取均值填充，可能会忽略某些重要信息或掺入噪声，对预测结果造成不良影响。一般归一化方法是采用去除均值和缩放到单位方差来完成。但异常值通常会以负面方式影响样本均值/方差。而RobustScaler标准化算法的鲁棒性好，可根据四分位数、中位数对每个特征进行独立的居中和缩放，能更好的的处理离群点，降低异常值对样本的影响，产生更好的预测结果。

3 短期负荷预测模型

3.1 传统LSTM算法

LSTM网络是通过一种被称为存储块的结构对数据进行丢弃或者添加信息。典型的LSTM 神经网络包括多个层，包括序列输入层，LSTM层和回归输出层。 LSTM层的基本单位称为存储块，存储块的内部架构如图3。

图3 LSTM神经网络体系结构

f

(

τ

)=

σ

(

W

x

(

τ

)+

U

h

(

τ

-1)+

b

)

(9)

i

(

τ

)=

σ

(

W

x

(

τ

)+

U

h

(

τ

-1)+

b

)

(10)

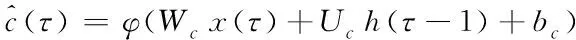
(11)

o

(

τ

)=

σ

(

W

x

(

τ

)+

U

h

(

τ

-1)+

b

)

(12)

(13)

h

(

τ

)=

o

(

τ

)⊗

φ

(

c

(

τ

))

(14)

使用sigmoid函数(

σ

)和双曲正切函数(

φ

)作为激活函数。 特殊符号“⊗”用于表示按元素的乘法。元素函数

σ

和

φ

定义如下

(15)

(16)

3.2 基于LSTM神经网络的单步预测算法

LSTM NN的输入数组包含多个矩阵单元。如下准备时间步长(

τ

-1)的输入矩阵单元：选择回溯时间点的数量，即输入序列长度

M

。

输入特征序列的方式如下：

过去

M

个时间步的每小时电负荷为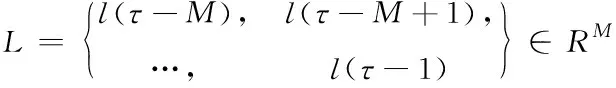

(17)

将过去

M

个时间步长的每小时温度设置为

(18)

将过去

M

个时间步的每小时相对湿度设置为

(19)

将星期特征设置为

P

∈

R

， 其中

P

∈

N

，1≤

P

≤7。

当今智能电表基础设施(SMI)采集的历史负荷缺失异常值较少，文中在含有少量异常值基础上，保持负荷及相关数据的原始性，不直接对数据做缺失异常值处理，而是在数据归一化阶段采用Robust标准化方法来针对离群点做出处理。

最后，归一化的输入特征以(10×

M

)输入矩阵阵列的形式为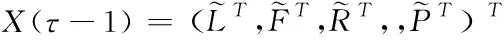

(20)

此后，通过堆叠两个LSTM层来获得深度学习网络。 第一个LSTM层按顺序接受输入矩阵阵列，并为每个完整的输入序列样本更新M次存储块。 第二层LSTM层存储块与第一层同步更新。第二层中与序列中最后一个时间步相对应的最后更新输出被发送到输出层以生成标量输出。此输出是预测的下一步负荷为

Y

(

τ

-1)={

l

(

τ

)}∈

R

。

3.3 检测流程

设计的预测方法总体流程如图4。

图4 改进LSTM流程图

1)特征选择与预处理：对原始数据集利用MIC特征选择技术选出与历史负荷相关性较大的因素，然后进一步利用随机森林与递归特征消除(RFE)选取强相关性特征，处理过程中采用对含有少量异常值，鲁棒性好的Robust标准化方法对数据归一化；

2)将数据转化为输入准备数据形式，训练单步预测的LSTM模型；

3)结果与评价：最后经单步预测模型输出最终预测结果。根据负荷需求输出预测值和真实值评价指标MAE，RMSE和MAPE对预测结果做出评估，并在GRNN和ELM中实现相同的单步预测算法来对LSTM的预测模型进行比较。

4 结果分析

误差评估指标采用平均绝对误差(MAE)，平均绝对百分比误差(MAPE)和归一化均方根误差(RMSE)，公式如下：

(21)

(22)

(23)

其中，

n

为预测点个数。

训练模型使用2012年至2014年期间的数据集进行训练，而2015年的数据集用于测试算法。第一和第二个LSTM层分别包含55个神经元和50个神经元。

预测模型的性能对输入序列的长度很敏感。因此，探索了具有不同输入序列长度，即回溯时间窗口中不同时间步长的算法的性能，以确定最有效的序列长度。18步序列实现了最低的误差，见表1。因此，使用18步预测算法来训练和测试所提出的模型。

表1 LSTM单步算法预测性能

由于每日负荷曲线随季节变化，因此，通过不同季节对模型的预测准确性进行了研究，结果见表2。

表2 单步预测模型对季节变化的预测

为了研究季节性影响，使用移动平均法对每个季节每个月的实际负荷曲线进行平滑处理，以创建基本负荷曲线(Pb)。从实际负荷轮廓减去基本负荷轮廓，以将波动量化为波动。最后，通过将Pb视为信号，将Pf视为噪声，来计算信噪比作为挥发性度量。根据表2，在夏季出现的最低预测误差具有最小的波动性度量如图5。单步预测模型的性能如图6。

图5 季节波动对负荷的影响

图6 单步负荷预测模型性能

通过在GRNN和ELM中实现相同的算法来对基于LSTM的预测模型进行基准测试。单步负荷预测模型通过18步回溯窗口实现。冬季三天的预测比较如图7。

图7 单步负荷预测模型的比较

下面对不同算法在单步负荷预测算法上的性能进行了比较见表3。

表3 预测性能比较

从表3中可知，LSTM网络相比其它两种算法具有优越性。

5 结论

针对智能电网下影响负荷因素众多、负荷数据存在少量缺失异常值和序列非平稳性的特点，提出了一种基于最大信息系数(MIC)与小波分解的双模型集成的短期负荷预测模型，并通过真实电网数据进行了验证。得出以下结论：

1)影响负荷的因素众多，利用适用于非性数据的最大信息系数MIC选出相关性大的影响因素，再使用随机森林并结合递归特征消除(RFE)选取强相关特征，可提高预测精度。

2)预处理过程中，未直接对少量缺失异常值处理，这样保证了数据的原始性。在归一化时通过对异常值敏感的Robust标准化方法间接对异常值作出处理，解决异常值的问题。

3)选取高维数据预测良好模型LSTM进行改进，改进后的单步预测LSTM模型，可有效避免了过拟合和梯度消失问题。并且在与其它两种算法相比，LSTM网络生成的模型拥有更强的泛化能力，进一步提升负荷预测精度，而且在实际应用中更具有价值。