基于扰动观察的双馈风电场有功功率自动控制

陈丽敏，齐红伟

(1. 青岛科技大学自动化与电子工程学院，山东 青岛 266000；2. 江苏师范大学电气工程及自动化学院，江苏 徐州 221116)

1 引言

由于电力技术水平提升，风力发电机经过多次更新换代，双馈型感应发电机具有运行稳定、体积小等优点被广泛应用，该发电机的控制器对数学模型依赖性较强，且数学模型建立过程中的假设条件存在一定偏差，使风电场的有功功率与实际需求存在一定的偏差，为此需要对双馈风电场有功功率进行有效控制。在众多风电场有功功率控制方法中，何秀强等人设计的孤岛启动与并网控制方法利用空载运行方式实现有功功率控制，但受输送端母线交流电压和频率变化的影响，使其控制耗时较长，因此控制效果不理想。荣飞等人设计的损耗最小化有功功率控制方法以降低风电机损耗方式实现有功功率控制，虽然较好地实现了风电场有功功率控制，但降低变流器设备功率方式仅适用于小型风电场。

扰动观察方法以扰动方式对风电场输出电压进行干预，依据其输出功率数值实现最佳功率跟踪。为此本文设计基于扰动观察的双馈风电场有功功率自动控制方法，为风力发电行业发展提供相应技术支持。

2 基于扰动观察的双馈风电场有功功率自动控制

2.1 双馈感应发电机运行原理

风力发电系统使用双馈感应发电机通过风作用到其桨叶上使其转动，且可在风力不同，桨叶转速不同的情况下输送电恒频与电恒幅，其发电结构如图1所示。

图1 双馈感应发电机发电结构示意图

双馈感应发电机可按照电网需求合理配置励磁电流幅值、频率等，其运转模式为异步运行，假设该电机的转子速度、受励磁电流影响形成的与旋转磁场相对的转子转速和同步转子转速分别为

c

、

c

、

c

，则三种转速关系表达式如下

c

=

c

+

c

(1)

假设该电机的转子频率、励磁频率和电网频率分别为

f

、

f

、

f

，则三种频率关系表达式如下

f

=

f

+

f

(2)

通过式(2)可知，对发电机励磁电流频率的合理配置可使定子侧的工频电能保持稳定状态。

2.2 双馈感应发电机数学模型

在建立双馈感应发电机数学模型时，利用

dq

坐标轴分量表示发电机相变量，令坐标轴内两个轴方向的参数为一一对称关系，依据发电机惯例，建立双馈感应发电机电压方程如下

(3)

上述公式中，坐标轴内

d

轴的定子与转子电压分量为

u

、

u

，

q

轴的定子与转子电压分量为

u

、

u

，

d

轴的定子与转子电流分量为

i

、

i

，

q

轴的定子与转子电流分量为

i

、

i

，

d

轴的定子与转子磁链为

δ

、

δ

，

q

轴的定子与转子磁链为

δ

、

δ

，定子绕组电阻由

R

表示，转子绕组电阻由

R

表示，

ω

则表示角速度，微分算子与滑差分别由

p

、

s

表示，

ω

为风频。

双馈感应发电机磁链数学模型为

(4)

上述公式中，定子与转子的绕组等效自感由

L

和

L

表示，定子与转子之间的等效互感由

L

表示。

双馈感应发电机转矩数学模型为

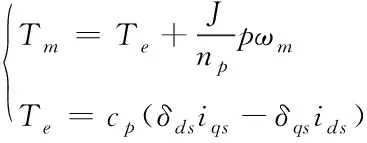
(5)

上述公式中，

ω

表示转子机械旋转角速度，电机对数由

c

表示。

双馈感应发电机功率数学模型为

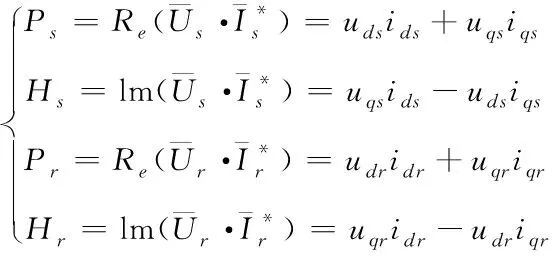
(6)

2.3 双馈感应发电机动力学模型

在双馈感应发电机发电结构内，风为风力机提供的机械功率表达公式如下

(7)

(8)

上述公式中，

ω

表示风力机机械角速度。

风能利用系数表达公式如下：

(9)

其中，

λ

的表达公式如下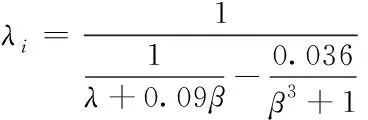

(10)

分析风能利用系数公式函数特点得出，当扇尖速比为固定数值时，风能系数与桨距角呈反比例关系，当桨距角为固定数值时，扇尖速比和风能系数的最高数值互相对应，当风速条件相同时，可通过变更风力机旋转速度时风能利用系数达到最高数值。

令

Z

(

ω

)表示风力机的等效阻抗，其计算公式如下

(11)

上述公式中，风力机等效电阻和等效电抗分别由

F

、

X

表示，风力机质量、附加质量和阻尼系数分别由

m

、

m

、

F

表示，

j

为可变常数。

通过式(11)可知，风力机的等效阻抗、等效电抗与电流和电压性质相同。

当大气运动较稳定的情况下，风速在某时间段内，风速变化情况不明显，此时视为风力机具有稳定频率，因此，风力机的附加质量与阻尼系数表达式如下

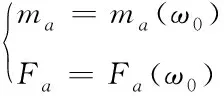
(12)

上述公式中，

ω

表示风力机稳定频率。

将风力机处于稳定频率时的附加质量和阻尼系数数值代入到式(11)内可知，稳定风速情况时风力机的等效阻尼和风频率具有固定物理特性，此时风电场有功功率表达式如下

P

(

ω

)=

(13)

上述公式中，弹性系数由

K

表示，

O

表示风作用在扇叶上的力，利用上述步骤可获取双馈风电场动力参数。

2.4 基于扰动观察风电场有功功率控制方法

依据双馈风电场动力学模型和数学模型获取风电场相关参数，其有功功率自动控制可利用变更风力机浆距和发电机励磁电流的方式实现，在功率控制方面分为有功功率控制和无功功率控制，前者可通过获取最高风能数值表达，即利用改变发电机转速使风力机在切入风速与最高转速过程中，其风能利用系数数值达到最高，而无功功率控制可利用恒功率因数与恒电压实现控制，恒功率因数与恒电压以变更无功功率参考数值，通过控制器励磁电流与电压使风电场输出的无功功率发生变化，为使风能发挥其最大效应，在恒功率控制无功功率时，功率因数设置为常数1，当利用恒电压方式控制无功功率时，以风电场与电网交接位置电压作为控制电压，因此无功功率变化数值为风电场与电网交接位置电压上下浮动之差。

利用式(13)可知，当风频率保持恒定的情况时，有功功率受阻尼系数和弹性系数影响表现为单峰值特点，此特性即为风力双馈风电场有功功率输出特性，其表现为在某特定风频率下，利用阻尼系数与弹性系数构成的二维变量组使风电场输出的有功功率数值最大。由于二维变量组的存在，无法利用单维度扰动观察方式获取最佳风电场输出有功功率，因此，需要在两个维度上增加阻尼系数与弹性系数交替扰动情况的第三维度，通过两两比较的方式获取阻尼系数变化情况，从而获取最大有功功率数值。本文利用分区域式变步长扰动观察方法实现风电场有功功率控制，该方法通过斜率计算区域变更速度，经过对固定步长与斜率变步长添加扰动后，以寻找最佳数值方式降低功率点上下变化情况。当时间为

k

时，计算风电场的输出功率数值，依据该功率数值曲线斜率角划分为三个有功功率控制区域，区域的斜率角度数分别为0～30度、30～150度和150～180度，通过判断角度分区，对有功功率以变步长的方式进行扰动并判断扰动方向，依据扰动情况，更新风电场有功功率、阻尼系数以及弹性系数数值，从而实现风电场有功功率控制。分区域式变步长扰动观察控制流程如图2所示。

图2 分区域式变步长扰动观察控制方法

3 实验分析

以某省大型双馈风电场为实验对象，该风电场配置为：装机容量202MW，联络线电阻0.309Ω，功率约束限值41.3MW，风电场升压站电压等级110kV，为更加精准呈现本文方法控制效果，依据实际双馈风电场运作数据，利用MATLAB仿真软件模拟双馈风电场运行，并利用本文方法、文献[3]方法和文献[4]方法对该风电场有功功率展开控制，其中，文献[3]方法和文献[4]方法分别表示孤岛启动与并网控制方法和损耗最小化的有功无功协调优化控制方法。

设置仿真时间为400s，风频率分别为0～180s时保持时间为4s，风频率为180～360s时，其时间周期呈现不断变化趋势，风频率为360～520s时，风频周期为6s，分别使用三种方法对该双馈风电场有功功率进行控制，利用仿真软装输出其风能捕获曲线，结果如图3所示。

图3 三种方法风能捕捉能力测试结果

分析图3可知，三种方法的风能捕捉率均随着时间的增加先呈现直线式上涨而后保持相对稳定状态，其中，文献[3]方法和文献[4]方法的风能捕捉率分别在时间为140s和50s时达到相对稳定数值，但二者的风能捕捉率均出现不同程度的波动情况，表明两种控制方法控制状态不佳，而本文方法的风能捕捉率在时间为25s左右已开始保持稳定状态，且风能捕捉率数值始终保持在0.98左右，当时间为400s左右，其风能捕捉率数值接近1.0，远高于对比方法，由此可知，本文方法控制双馈风电场的风能捕捉效果较好。

在仿真软件内设置电压急速下降工况，绘制三种方法控制下的直流电容电压变化曲线，结果如图4所示。

图4 三种方法控制的双馈风电场直流电容电压曲线

分析图4可知，文献[3]方法和文献[4]方法控制的风电场电容电压曲线波动幅度较大，曲线振荡时间较长，表明两种方法控制的电容电压不稳定，控制效果较差，而本文方法在时间为0.22s之前控制的电容电压曲线虽存在一定波动幅度，但波动数值较低，当时间超过0.22s后，本文方法控制的电容电压曲线较为平缓，波动起伏不大，表明本文方法控制的风电场有功功率回路与无功功率回路之间的解耦关系较好，有功功率的变化对风电场直流电容电压影响较小。

绘制三种方法控制下的风电场无功功率曲线，对比三种方法控制无功功率补偿有功功率效果，结果如图5所示。

图5 三种方法控制无功功率补偿有功功率效果

分析图5可知，文献[3]方法和文献[4]方法控制的无功功率曲线波动较为相似，由于电压急速下降，下降后的风电场瞬态峰值相对较高，远高于风电场撬棒保护触发数值，从上图三种方法无功功率波形上看，无功功率曲线经过短暂的波动后返回到稳定状态，表明此时风电场有功功率得到有效控制，由此可见，本文方法可使风电场有功功率迅速恢复到其所需数值。

为更直观体现其有功功率控制效果，在仿真软件内设置额定有功功率数值，在不同风速情况下，测试三种方法有功功率控制情况，结果如表1所示。

表1 三种方法有功功率控制情况/kW

分析表1可知，随着风速的增加，三种方法控制的有功功率数值均出现不同程度偏差，其中，文献[3]方法和文献[4]方法控制的有功功率数值均出现两次偏差，二者偏差最大数值分别为39kW和22kW，而本文方法控制的有功功率数值在风速为90m/s之前均和额定有功功率数值相同，仅在风速为100m/s时出现轻微偏差，偏差数值仅为1kW，由此可见，本文方法控制双馈风电场有功功率效果较好。

4 结论

本文利用扰动观察方法对基于扰动观察的双馈风电场有功功率自动控制展开研究，依据有功功率受阻尼系数和弹性系数影响表现为单峰值特点，设计分区域式变步长扰动观察控制方法实现双馈风电场有功功率控制。实验结果表明：本文方法控制的双馈风电场风能捕捉率始终保持在0.98左右，控制双馈风电场的风能捕捉效果较好；控制电压曲线波动幅度较小，控制的风电场有功功率回路与无功功率回路之间的解耦关系较好；在不同风速条件下，控制有功功率与额定有功功率仅出现一次偏差，且偏差数值仅为1kW，控制双馈风电场有功功率效果较好。