基于蒙特卡洛法的涡扇发动机稳态试验性能分析方法研究

2022-07-19胡冰茜

燃气涡轮试验与研究 2022年6期

樊巍，胡冰茜，黄鹏，薛萱，陈文

(中国航发四川燃气涡轮研究院，成都 610500)

1 引言

涡扇发动机稳态试验性能结果是评定发动机能否达到设计要求的重要依据[1]。试验过程中，通过测试系统采集发动机不同截面的温度、压力以及推力、燃油流量等参数，依据试验性能计算模型，求解包括耗油率、燃烧室出口温度、压比、效率等参数，并根据测量和计算结果，对发动机稳态性能是否满足要求进行评定[2]。在发动机实际工程研制过程中，尤其是在发动机科研阶段，直接应用原始测量数据对性能进行分析，经常会出现发动机推力、耗油率或其他参数不满足设计要求，但具体数值与设计要求相差量值很小的情况。这种情况下，如果简单认为发动机性能不达标，就有可能导致大量不必要的试验或设计修改等方面的工作，影响试验结果评定的准确性。造成以上问题的原因主要是，发动机试验过程中，台架实际工作环境条件、测试系统的测量精度、测试探针安装偏差等系统误差的累积叠加，使得直接基于原始测量数据对发动机性能进行评定的方式，有可能偏离真实的工作状态。为此，有必要在发动机稳态试验性能评定过程中将这些影响因素考虑进去，并开展相关的研究工作。

国内外针对以上问题开展了大量的研究工作，且主要集中在以下两个方面：一是通过建立基于概率设计方法的分析模型，量化发动机各部件性能不确定性对发动机性能的影响，对发动机设计解域求解、性能退化、性能裕度容限等进行分析[3-6]；二是建立试验数据校核过的发动机稳态计算模型，依据发动机共同工作原理，利用敏感性等分析手段，判断可能造成发动机性能偏差的主要部件，进而对相关部件参数进行修正，获取发动机实际性能[7-9]。在实际的工程应用中，对于涡扇发动机稳态试验性能分析而言，设计人员希望能够考虑试验过程中的不确定性变化，并尽可能快地对结果进行判断。基于以上考虑，本文在稳态试验性能计算模型和概率论方法的基础上，利用蒙特卡洛法[10]在应用过程中可以忽略各种干扰因素之间的影响，建立了基于蒙特卡洛法的试验分析方法。通过考量各测量参数不确定性变化对最终结果的影响，获得满足性能结果评定的达标区间，提高了性能结果评定的准确性和科学性。

2 稳态试验性能计算模型

以双轴混排涡扇发动机为研究对象，基于部件法[11-13]建立了针对稳态试验分析的性能计算模型，并开发了相应的计算程序。发动机各截面定义如图1 所示。测试方案见表1，表中还根据具体采用的测量探针的说明书，给出了每个测量参数的测量误差。利用试验过程中测取的截面温度、截面压力、燃油流量、推力、转速等参数，根据流量平衡、功率平衡、动量平衡等约束方程，采用变比热计算方法[12]，计算并获取发动机推力、耗油率、进口流量、部件压比、部件效率等性能参数。

表1 发动机测试方案Table 1 Engine test plan

图1 发动机结构示意图及测试截面定义Fig.1 Engine layout and test section definition

针对稳态试验性能计算模型，需说明两点：①受限于测试技术手段，无法有效、长时间地测量高压涡轮进出口的温度和压力[14]，导致无法直接通过测量数据对高、低压涡轮性能参数进行计算；②受测试技术手段和发动机本身结构限制，核心机进口流量或涵道比无法通过直接测量获得。针对以上问题，经相关研究人员大量研究[8，14-17]，一般采用核心机特性插值法[15]、涡轮换算流量法[8，14，16]、热平衡计算法[8，17]获得满足工程精度要求的试验结果。应用过程中，也可根据实际情况择优选择相关方法，具体方法本文不再赘述。为方便讨论，下文分析中采用涡轮换算流量法，利用试验前高、低压涡轮喉道面积吹风测量结果，在模型中通过给定高、低压涡轮喉道换算流量的方式进行稳态试验性能计算。

3 基于蒙特卡洛法的分析方法

基于蒙特卡洛法的试验性能分析方法的主要步骤为：①对获取的原始测量数据进行处理后，采用蒙特卡洛法生成随机数并确定样本容量，确定并计算获取性能评定参数结果；②求解性能评定参数的不确定度，获取性能评定参数的达标区间。

3.1 原始测量参数的处理

对于试验性能分析模型，需要对每个截面中原始测量的温度和压力分别平均后才能进行计算。对测量参数进行平均的方法有多种，通过对不同类型发动机在实际工程应用中的试验数据总结，经过对发动机测试位置精细化处理和验证，一般都可以通过数值平均的方式获取截面的测量平均值[1，17]。根据中心极限定理，当独立随机变量影响叠加时，即使各变量本身不服从正态分布，但其和趋向于服从正态分布，且多个正态分布的任意线性组合仍服从正态分布，通过平均方式获取的截面参数服从分布[18]。

3.2 性能评定参数的确定

3.3 达标区间的确定

采用蒙特卡洛法对平均后的测量参数进行抽样，在保证足够抽样数量的基础上，获取服从正态分布的不确定性变化参数，通过求解不确定度来确定性能评定参数的达标区间。对于抽样数量而言，样本容量越大，相关参数的均值和标准差越小，计算时间越长。为了能在试验过程中快速分析性能达标情况，样本容量的选择还应考虑实际情况。具体计算步骤为：

(1) 根据3.1 节确定原始测量参数平均后的概率密度函数，并在不同样本容量条件下，依据概率密度函数进行随机抽样；将每组抽样参数带入稳态性能计算模型，获取性能判定结果参数样本yi；按照式(1)计算判定结果参数均值，采用式(2)获得判定结果参数标准差S；判断不同样本容量条件下计算结果的均值和方差是否随着样本容量的变化趋于平稳，并将满足要求的样本容量m作为程序中的设定值。需要特别说明的是，蒙特卡洛法中产生随机数的方法很多，为方便工程应用，本文采用文献[10]提出的产生伪随机数的方法。

4 算例与分析

以某型双轴混排涡扇发动机地面最大状态性能调试试验的稳态性能数据为例，对本文提出的方法进行验证。需要说明的是，下文算例中的主要性能参数，均已按照蒙特卡洛法模拟后的试验值除以设计值的方式进行了归一化处理。

按照上文提出的方法，首先对试验中采集的原始数据进行平均处理，然后对不同样本容量下的发动机性能进行计算，依据推力和耗油率蒙特卡洛法仿真结果确定仿真迭代次数。其平均值和标准差随样本容量的变化关系分别如图2、图3 所示。可以看出，当样本容量大于10 000 后，均值和标准差基本保持不变，故文中样本容量设置为10 000。

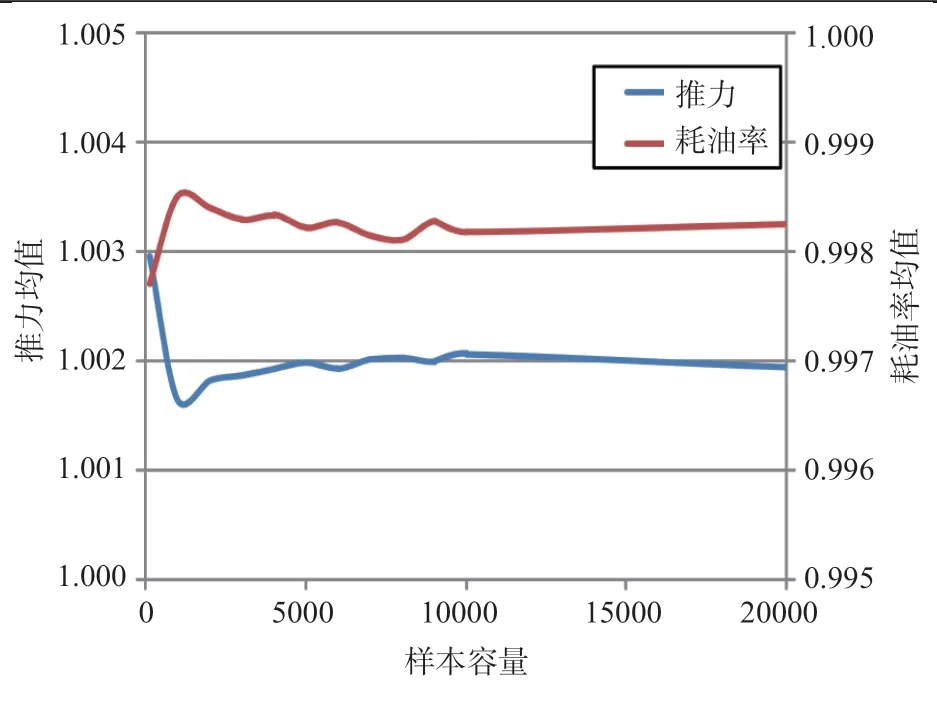
图2 均值随样本容量的变化关系Fig.2 Relationship between mean value and sample size

图3 标准差随样本容量的变化关系Fig.3 Fig.3 Relationship between standard deviation and sample size

采用相同的稳态性能计算方法，将本文提出的方法与不考虑测量不确定性变化直接计算得到的结果进行对比，结果见表2。可以看出，在本次试验中，采用直接计算获取的sfc偏高，T4偏高，偏低，偏低，但距离设计值的相对误差均在1%以内。从采用本文提出的方法获得的达标区间可以看出，sfc、T4、均在达标区间范围内，发动机真实性能已经达标。造成直接计算结果存在偏差的主要原因，为测量参数的不确定性分布所致。