基于伴随法的空气系统引气管减阻优化设计

梁津华，赵维维，邹 咪，马建栋

(中国航发四川燃气涡轮研究院，成都 610500)

1 引言

在航空发动机空气系统中，引气管的作用是将压气机温度较低的空气，引到涡轮等高温部件，用以叶片冷却、级间封严、轴承封严等。引气管设计应在满足引气要求的条件下，尽量实现尺寸小，质量轻。由于引气管结构简单，在空气系统设计时常不受重视，且当引气量不满足要求时，往往直接通过增大管径的方法来解决，缺乏对引气管的精细设计，导致引气管的流动损失较大。为此，对引气管进行优化设计，减小流动损失，减轻引气管质量，对提升发动机效率具有重要意义。

多位学者对空气系统引气管开展了研究工作，针对管路的应力、布局等进行了优化，但对管路流动损失的优化研究不足。如陈艳秋等[1]采用遗传算法对航空发动机管路进行了优化，快速高效地获得了满足工程要求的应力分布最优解。陈志英等[2]对航空发动机空气管路应力进行了优化设计，获得了三通结构尺寸的优化结果，降低了总应力和附加载荷应力。赵柏萱等[3]提出了一种基于工程规则的管路自动布局与综合优化技术，采用运动规则算法对管路进行布局，通过模拟退火法对布局方案进行优化，并通过实际应用验证了技术的有效性。本文针对发动机引气管，采用伴随法，利用CFD 计算结果自动指出如何修改管路形状、降低流动损失，可为空气系统引气管减阻优化设计提供参考。

2 研究对象

研究对象为发动机引气管，其模型如图1 所示。引气管左边为进口，右边为出口，中间存在拐弯。进口给定总压313 kPa，总温900 K；出口给定静压260 kPa。用多面体网格对模型进行网格划分(图2)，并设置边界层。对网格进行无关性验证，结果如表1 所示。可见，当网格数大于36 万时，流量不再变化。为此，选择网格数36 万进行计算。

表1 网格无关性验证结果Table 1 Mesh independence verification results

图1 引气管模型Fig.1 The model of air bleed pipe

图2 网格划分Fig.2 Mesh

3 数值方法

3.1 计算方法

数值计算采用求解黏性N-S 方程的方法，控制方程的离散为有限体积法。采用二阶迎风格式对方程的对流项进行离散，采用中心差分格式对扩散项进行离散，离散方程的求解为隐式耦合求解，即连续方程和动量方程同时求解。湍流模型为SST模型，采用多重网格法加速收敛。

3.2 优化方法

优化方法采用伴随法[4-6]，求解微分方程得到目标函数对设计变量的敏感性。在流体力学中，优化问题的目标函数(如流量、压比等)均可表示为守恒流动变量和设计变量的积分函数：

3.3 网格变形方法

网格变形方法是通过改变网格节点坐标使网格形状发生变化[7-8]。相比于网格重构，变形前后相同的网格类型和拓扑结构，避免了网格离散误差对计算结果产生的干扰。网格变形采用基于径向基函数的方法，通过控制点实现。每个控制点都有1 个位移向量，利用这些点的位移向量建立插值场用以计算所有网格节点的位移，插值方法为径向基函数法[9]。

控制点的位移计算公式为：

3.4 参数定义

(1) 总压损失系数

4 优化

4.1 优化目标及变量

引气管优化的目的是降低流动损失，因此优化目标选择总压损失系数，即目标函数；优化变量为控制引气管网格变形的控制点。

4.2 敏感性分析

获得引气管流场后，求解伴随方程，得到总压损失对引气管壁面的敏感性，如图3 所示。图中，色卡图代表压力对壁面形状的微分。可看出，引气管头部和尾部拐弯处的敏感性最强，说明改变此处引气管形状对总压损失系数影响最大。

图3 引气管的敏感性Fig.3 The sensitivity of the air bleed pipe

4.3 网格变形

在引气管外面设置控制点(图4)，用以驱动引气管网格变形。控制点的位移量通过敏感性计算得出。由于引气管设置在机匣外，为避免与其他零件干涉，引气管中部做成了拐弯的形状。在网格变形过程中，为保持引气管的这种拐弯，需给定约束，图5 为引气管的约束段。约束段在网格变形过程中保持不动。

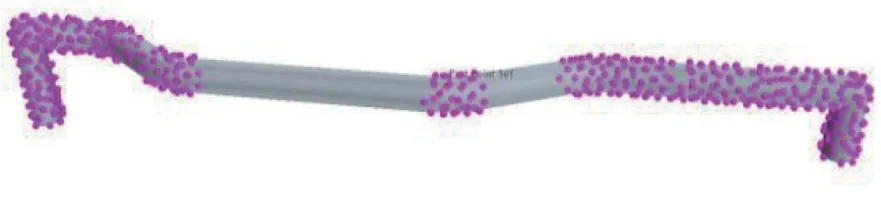
图4 控制点Fig.4 Control points

图5 约束段Fig.5 Constraint section

4.4 优化流程

针对引气管优化，首先进行三维流动计算，获得三维流场；接着采用伴随法，求解伴随方程，获取优化目标对引气管壁面的敏感性；根据敏感性，采用自定义函数移动控制点，改变引气管形状；最后对新的引气管进行三维流动计算，获得流场。根据优化目标能否满足要求决定是否继续优化，优化流程如图6 所示。

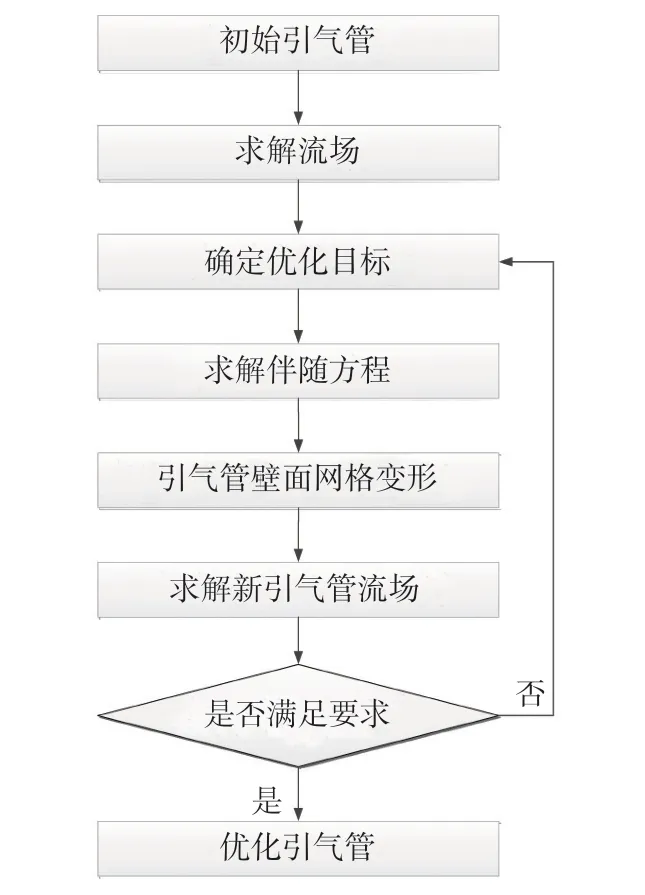
图6 引气管优化流程图Fig.6 Flow chart of the optimization for the air bleed pipe

5 结果分析

5.1 性能分析

引气管优化前后形状如图7 所示。引气管优化后的主要变化为，引气管头部和尾部拐弯处形成1个圆弧，在出口处形成1 个倒勾形状。引气管优化前的总压损失系数为0.115，优化后的总压损失系数为0.060，降低了47.83%；引气管优化后质量流量增加45.10%。

图7 引气管形状Fig.7 The shape of the air bleed pipe

5.2 流场分析

图8、图9 分别示出了引气管优化前后中截面头部速度和尾部速度。可看出，引气管优化前，其头部和尾部气流分离产生旋涡，造成引气管实际流通面积减小，气流被迫先加速后减速；引气管优化后，旋涡基本消失，气流实际流动面积增大，气流流动速度更加均匀。

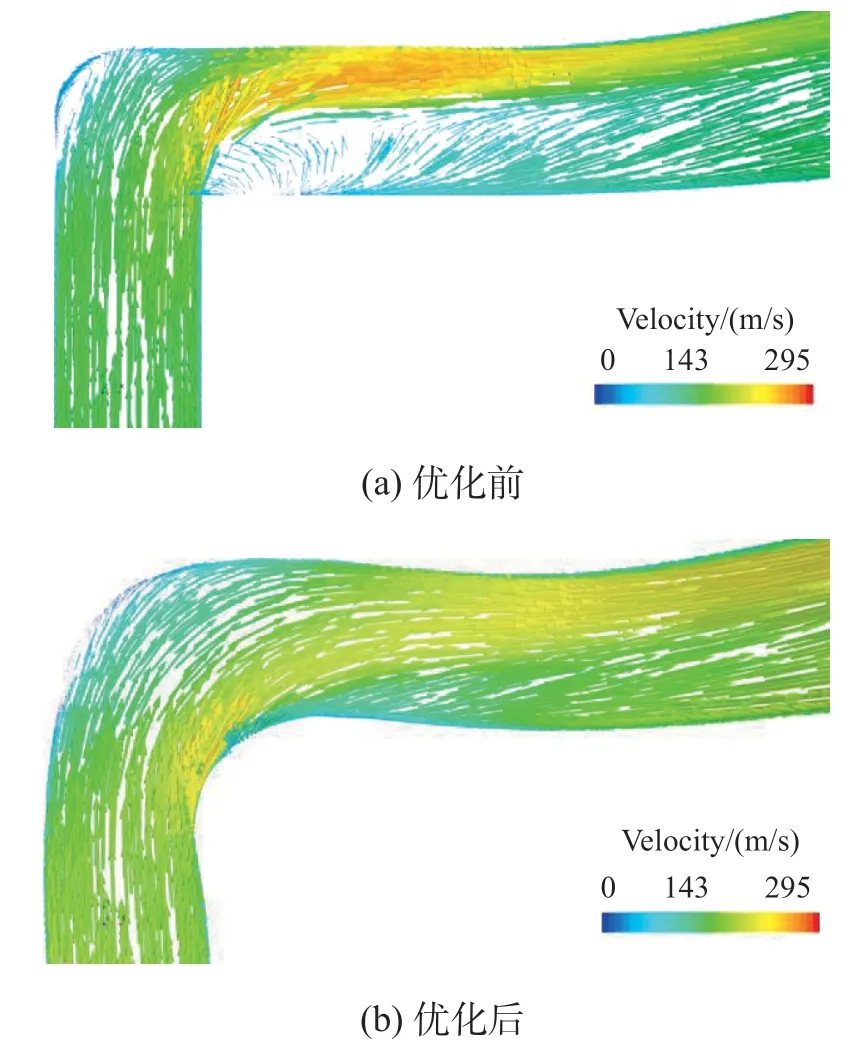
图8 引气管头部速度Fig.8 The head section velocity of the air bleed pipe

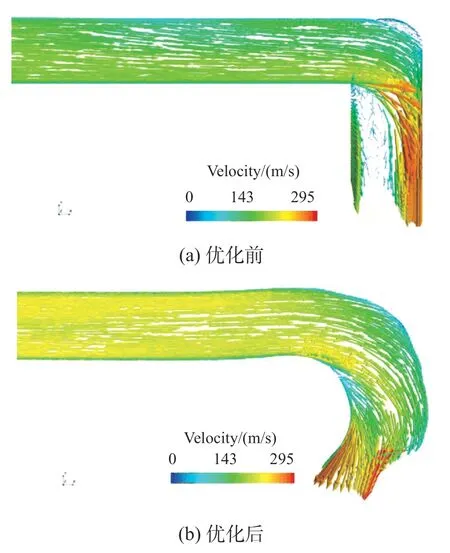
图9 引气管尾部速度Fig.9 The tail section velocity of the air bleed pipe

为分析引气管中的压力损失，根据引气管的形状特征，从引气管进口到出口截取了12 个截面，具体位置如图10 所示。图11、图12 分别示出了引气管优化前后中截面的总压云图和各截面的平均总压。可以看出，引气管优化前头部和尾部拐弯处有较大的总压损失，引气管优化后头部和尾部拐弯处的总压损失大幅降低，总压变化更平缓。

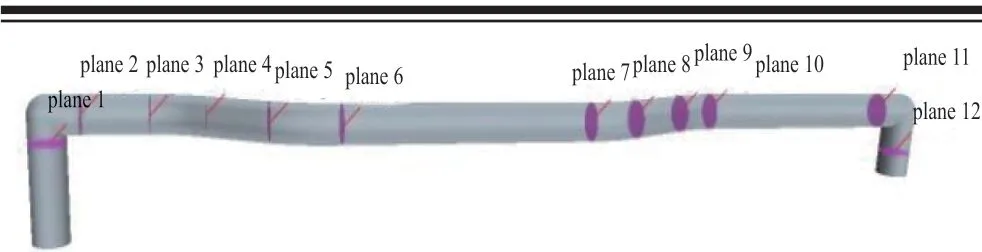
图10 引气管截面位置Fig.10 The plane positions of the air bleed pipes

图11 引气管中截面总压云图Fig.11 Total pressure of middle plane

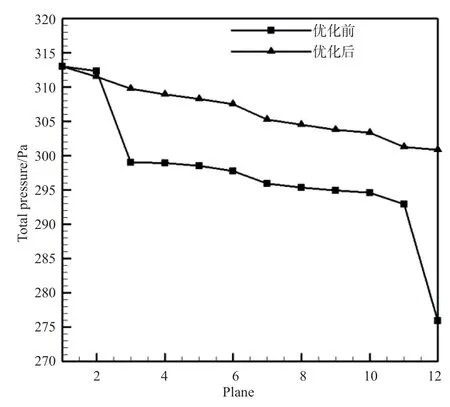
图12 引气管各截面总压对比Fig.12 The comparison of total pressure of planes

图13 示出了引气管优化前后中截面熵产。可以看出，引气管优化前头部和尾部拐弯处熵产较大，引气管优化后头部和尾部拐弯处的熵产明显减少。这是因为在初始引气管头部和尾部拐弯处，尖锐的拐弯内径使得气流流动方向急剧变化，并且旋涡的存在造成气流流动速度变化，而根据等熵流动理论，气流速度和方向变化越缓慢，流动过程越接近等熵流动，引气管优化后，拐弯半径变大，气流流动速

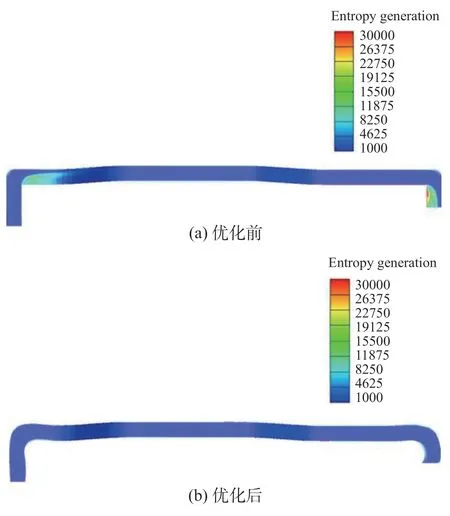
图13 引气管中截面熵产Fig.13 Entropy generation of the middle plane before and after optimization度和方向变化更平缓，熵产降低。

图14 示出了引气管优化前后中截面熵增。熵增为熵产从进口到目标位置的积分，可体现总损失大小。引气管优化前，头部和尾部气流分离产生流动损失，出口熵增为35.1 J/(kg·K)；引气管优化后，头部和尾部的分离损失明显减小，出口熵增为13.2 J/(kg·K)，降低62.4%，总损失大幅减少。

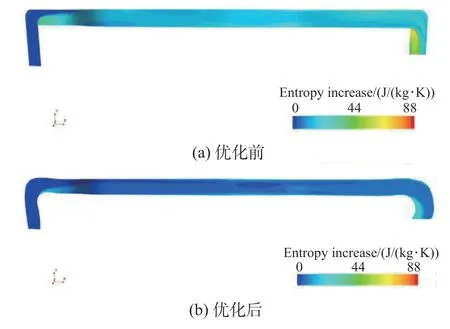
图14 引气管中截面熵增Fig.14 Entropy increase of the middle plane

6 结论

采用伴随法对空气系统引气管的总压损失系数进行了优化，通过对比分析优化前后数据表明了优化的有效性。研究得到如下结论：

(1) 引气管优化后总压损失降低47.83%，质量流量增加45.10%。

(2) 引气管优化后总压和速度变化更平缓，熵增大幅降低。

(3) 引气管的主要损失是因气流速度和方向急剧变化而产生，尖锐的拐弯会产生流动分离形成旋涡阻碍流动，平缓的拐弯更接近等熵流动，能够降低流动损失。