翼身融合水下滑翔机运动仿真分析

刘传奇，朱仲本，刘 杰

( 1.哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001；2.中国船舶科学研究中心 深海技术科学太湖实验室，江苏 无锡 214082)

0 引 言

传统回转体形状的水下滑翔机大部分是针对开阔的深海水域作业研发的[1-2]，而我国四大海区除南海平均水深在千米级外其他三大海区平均水深均为百米以内的数量级[3]。与深海水域相比，浅海水域水动力环境较为复杂，具有地形高度限制，加上浅海水域人类生产活动比较频繁，深海水下滑翔机无法适用作业，因此，研究如何增强水下滑翔机在浅海水域的滑翔能力已成为一种迫切的需求。

以翼身融合水下滑翔机为研究对象(见图1)，利用其升阻比大的水动力特性[4-5]增强水下滑翔机浅海水域滑翔能力，对其进行垂直面的运动仿真分析，从而得到有利于提高水下滑翔机对浅海水域复杂环境适用能力的设计方案和措施。

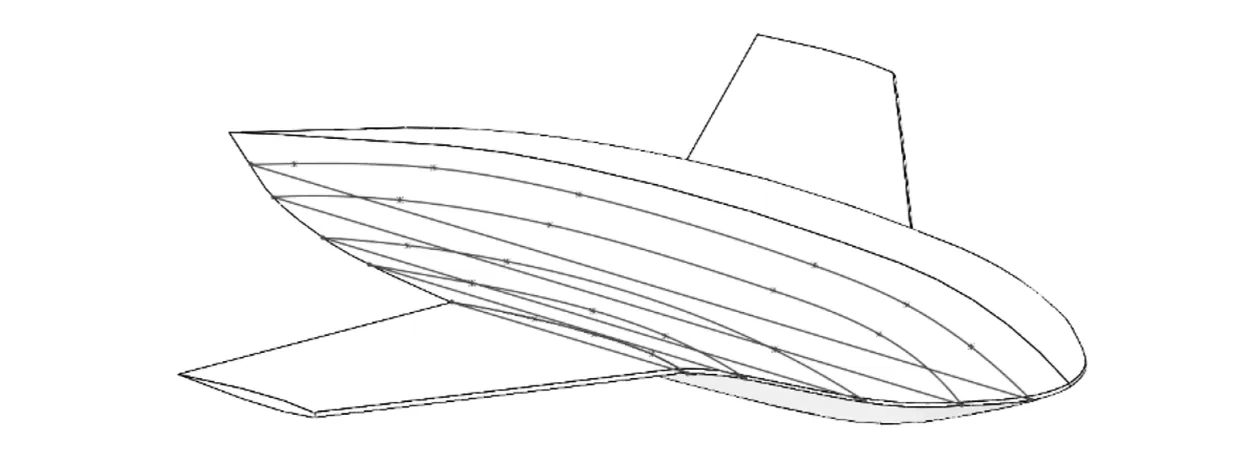
图1 翼身融合水下滑翔机概念图

1 动力学建模

将研究的水下滑翔机系统视为刚体，推导其运动学方程和垂直面内的动力学方程[6]，为后续的仿真系统搭建、开环响应分析和操纵性预报奠定理论基础。

1.1 坐标系定义

惯性坐标系和机体坐标系如图2所示。速度坐标系如图3所示。

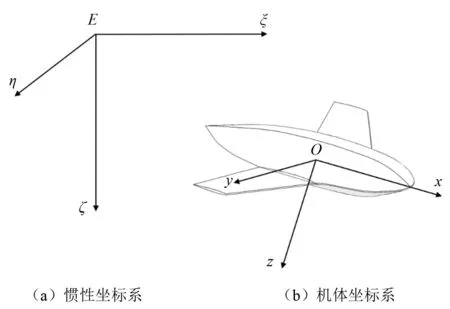
图2 惯性坐标系和机体坐标系示例

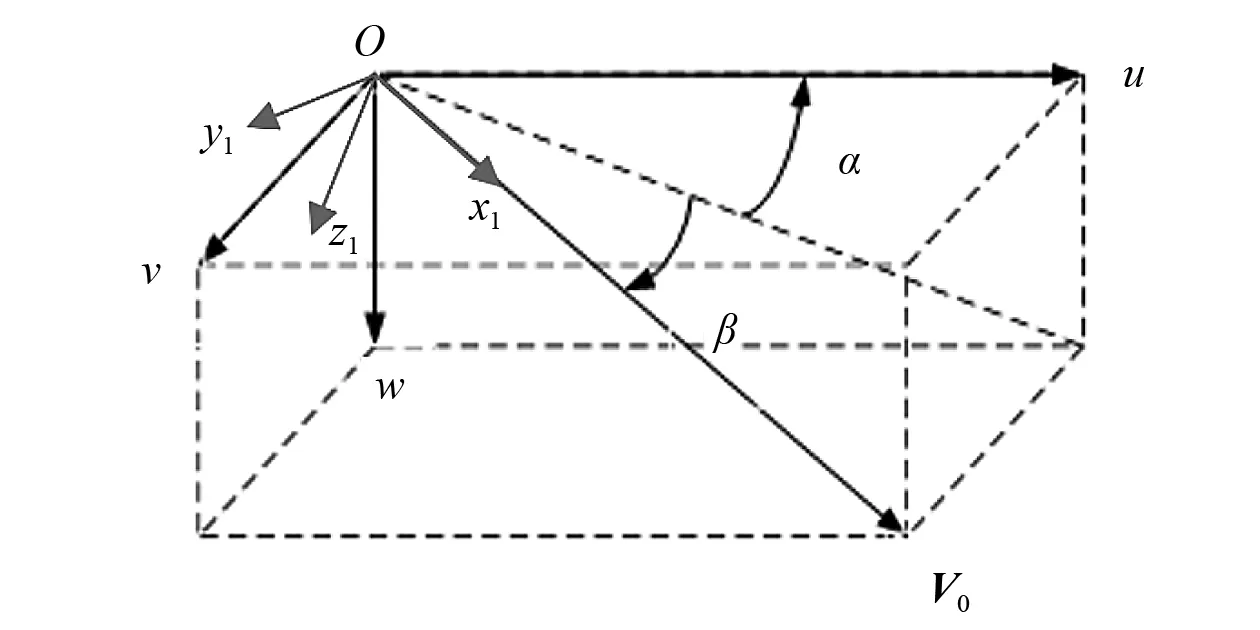
图3 速度坐标系示例

(1)惯性坐标系E-ξηζ

坐标原点E选择水下滑翔机试验水域的投放点；E-ξ位于水平面，指向北为正；E-η位于E-ξ轴所在平面，按右手法则顺时针旋转90°，指向东为正；E-ζ垂直于E-ξ和E-η所在平面，指向地心为正。

(2)机体坐标系O-xyz

坐标原点O选择在水下滑翔机的质心处；O-x轴经过坐标原点的水线面，指向机首为正；O-y轴经过坐标原点的横剖面，指向机身右舷为正；O-z轴经过坐标原点的纵中剖面，指向机身底部为正。该坐标系三轴速度分量分别为u、v和w。

(3)速度坐标系O-x1y1z1

水下滑翔机在机体坐标系中的航速及三轴分量为V0=(u,v,w)，以航速矢量为主轴建立速度坐标系；与机体坐标系具有攻角α和漂角β；坐标原点与机体坐标系原点重合；O-x1轴沿速度矢量指向前方；O-z1轴在滑翔机纵中剖面上垂直于O-x1轴指向机身下方；O-y1垂直于O-x1z1平面指向机身右方。

1.2 运动参数定义

角度参数和速度参数定义分别如表1和表2所示。

表1 角度参数

表2 速度参数

1.3 坐标转换

根据坐标转换理论得到运动学方程：

(1)

式中：Rbi为机体坐标系至惯性坐标系的线速度旋转矩阵，

Ω=TbiV0

(2)

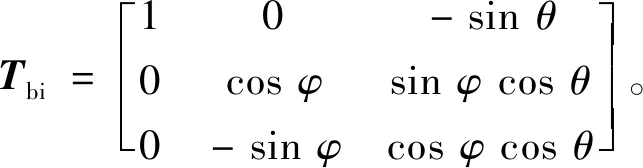
1.4 垂直面受力分析

水下滑翔机在机体坐标系垂直面上总的受力可分解为沿x轴的力、沿z轴的力及绕y轴的力矩，具体对应的力和力矩如下：

(1)惯性类水动力(矩)机体坐标系投影

(3)

式中：Xλ和Zλ分别为滑翔机在x轴和z轴上所受的惯性水动力分量；Mλ为绕y轴的惯性水动力矩分量；λ11、λ35及同形式的量为水下滑翔机在水下非定常运动时受到惯性力作用的附加质量。

(2)黏性类水动力(矩)机体坐标系投影

(4)

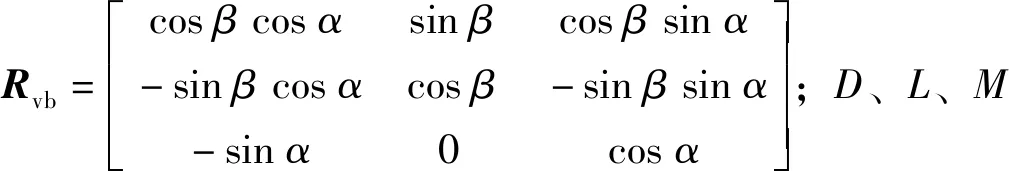
D、L和M的拟合公式为

(5)

式中：KD0、KL0和KM0分别为零攻角的阻力、升力和力矩系数；KD、KL和KM分别为攻角的阻力、升力和力矩系数；KΩ2为绕y轴旋转的力矩系数。

(3)静水力(矩)机体坐标系投影

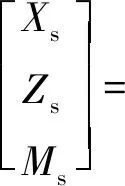
(6)

式中：Xs和Zs分别为滑翔机在x轴和z轴上所受的静水力分量；Ms为绕y轴的静水力矩分量；Fmx、Fmz和Mm分别为净浮力(矩)在机体坐标系下的投影；MB为调节浮力产生的恢复力矩；MP为调节滑块纵向位置产生的俯仰力矩；ΔV为从内油囊排至外油囊的油液体积；ρw为水的密度；g为重力加速度；rb1和rb3分别为调节净浮力产生的新的浮心在机体坐标系中的纵向和垂向坐标；ρo为液压油的密度；m为水下滑翔机的质量；mp、rp1和rp3分别为滑块的质量、纵向坐标和垂向坐标。

(4)控制力(矩)机体坐标系投影

根据点的速度合成定理和矢量变化率求导法得：

(7)

式中：Vp为滑块在机体坐标系下的线速度；Vo为质心在机体坐标系下的线速度；rp为滑块与质心之间的位移矢量；Pp为相应动量。

滑块对水下滑翔机的控制力Fp和力矩Mp在机体坐标系下投影为

(8)

垂直面展开的具体矩阵表达式为

(9)

式中：Xp、Zp和Mp分别为滑块对滑翔机的力和力矩在x轴、z轴和y轴上的分量；Pp1和Pp3分别为滑块动量在x轴和z轴上的分量。

综上所述，翼身融合水下滑翔机垂直面在机体坐标系受到的合力(矩)为上述所推导的全部力(矩)之和，因此其表达式为

(10)

式中：Xtotal和Ztotal分别为滑翔机在x轴和z轴上所受的合力；Mtotal为绕y轴的合力矩。

1.5 动力学方程

由文献[7]给出的水下航行器动力学方程可简化得到水下滑翔机在垂直面的动力学方程表达式为

(11)

式中：Iy为水下滑翔机绕机体坐标系y轴的惯性矩。

将式(10)代入式(11)展开化简,可得水下滑翔机垂直面运动模型为

(12)

式中：γ为水下滑翔机在惯性坐标系下的滑翔角。

2 开环运动响应仿真分析

在翼身融合水下滑翔机的运动模型建立后，通过仿真验证其可否正确描述水下滑翔机运动行为。在油囊体积调节量和滑块的纵向位置作为系统的输入量时，分析水下滑翔机相关运动性能指标的响应情况和范围，分析执行机构不同调节速度和布局对运动性能的影响。

2.1 执行机构调节速度对运动性能影响仿真

水下滑翔机模型的静力学参数和水动力参数采用文献[8]给出的同类型水下滑翔机数据，主要研究执行机构的不同参数设置对水下滑翔机运动的影响。仿真参数如表3所示。

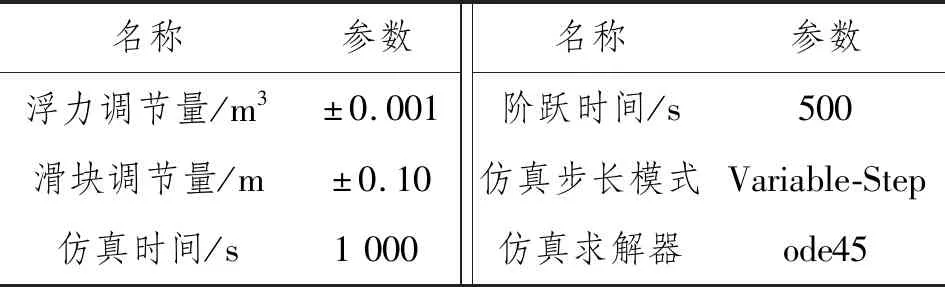
表3 Simulink仿真参数

浮力和滑块调节量为定值，通过设置不同的调节时间模拟执行机构不同的调节速度，阶跃调节和斜坡调节对应快速调节和缓慢调节，其仿真响应曲线如图4～图7所示。

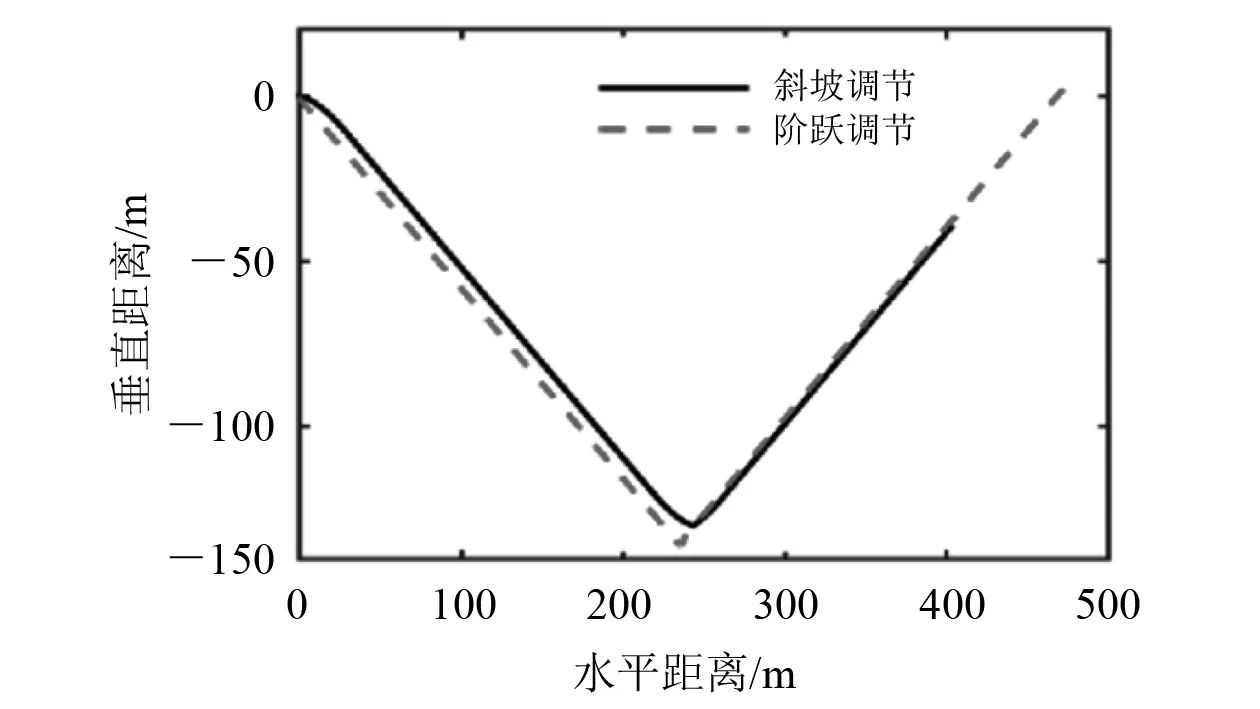
图4 轨迹对比

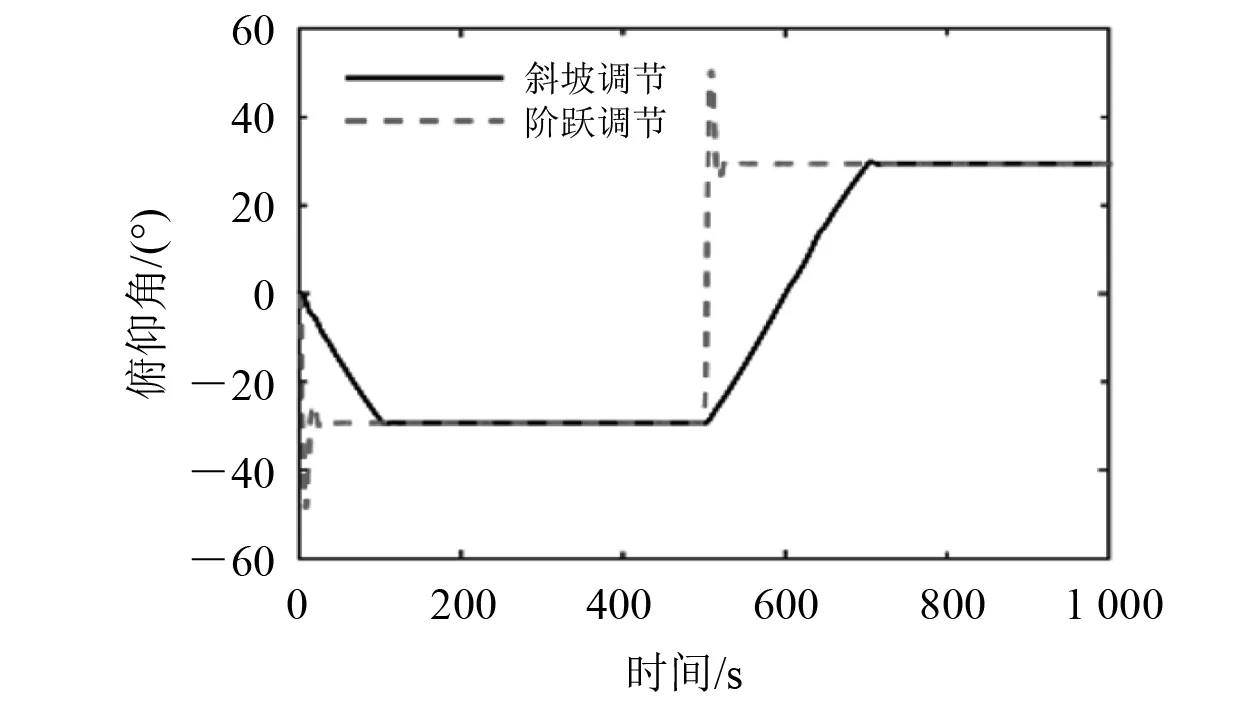
图5 俯仰角对比

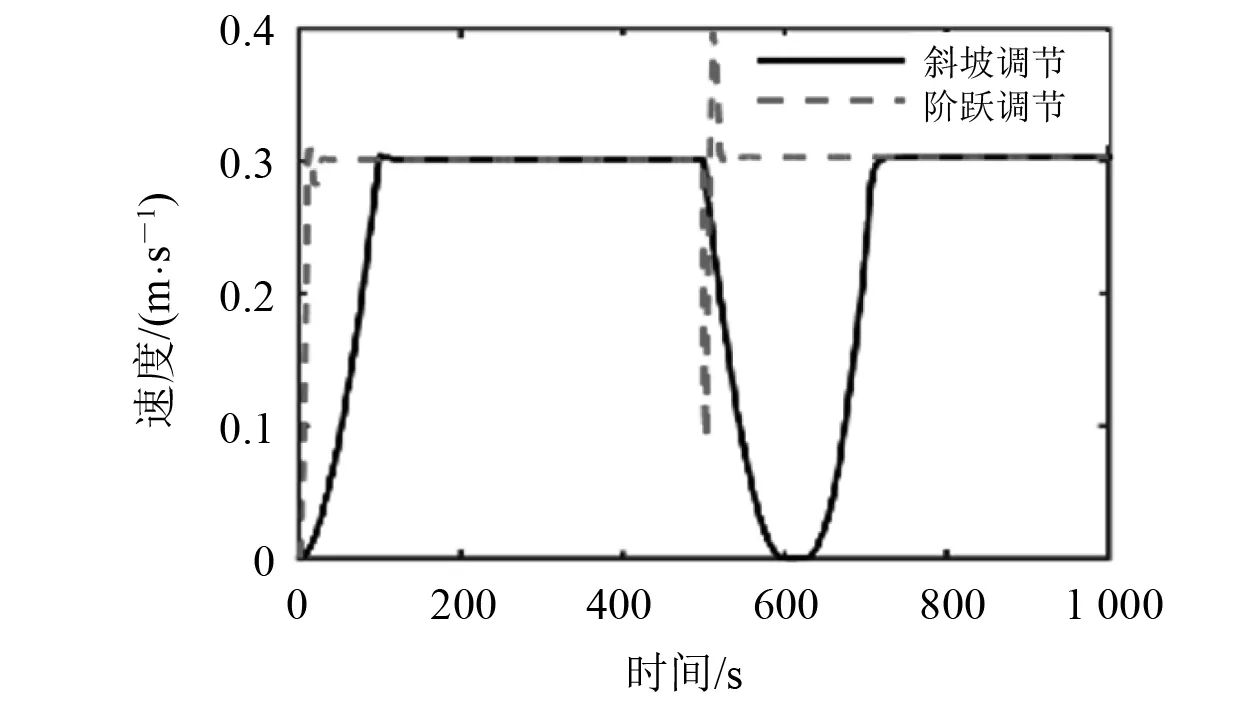
图6 航线速度对比

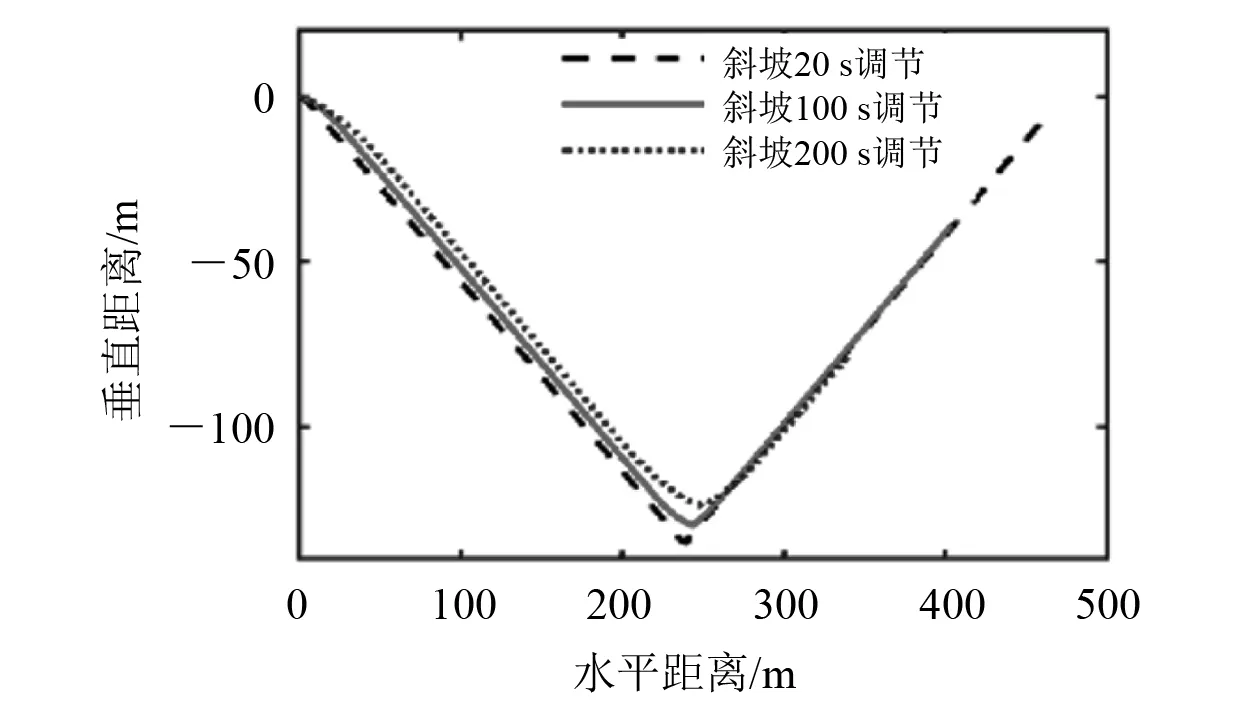
图7 不同斜坡轨迹对比

由图5和图6可知：斜坡调节和阶跃调节在各运动指标达到稳态后均相同，差别主要体现在调节的暂态过程，阶跃调节响应速度快，可短时间达到稳态；斜坡调节的俯仰角和速度的超调值均比阶跃调节小很多，各运动参数变化逐渐过渡，有利于水下滑翔机的稳定性。

由图4斜坡调节和阶跃调节垂直面运动轨迹对比可见：在相同时间内斜坡调节无论是垂直距离还是水平距离均比阶跃调节小，结合图6速度曲线与时间轴围成的面积，斜坡调节比阶跃调节的面积小，原因是斜坡调节过程耗时长，导致水下滑翔机稳态运动的时间变短。

图7对比调节时间为20 s、100 s和200 s的斜坡调节轨迹，可见：执行机构调节时间越长，水下滑翔机下潜的最大深度则越小，但整个运动周期滑翔的水平距离更远。

2.2 浮力调节机构布置对运动性能影响仿真

浮力调节机构布置在水下滑翔机的不同部位是否会产生显著影响，若有影响则布置在何处更有利于水下滑翔机的滑翔运动，这些问题均有待于通过仿真进一步分析。在Simulink仿真中设置的浮力调节机构布置参数如表4所示。

表4 浮力机构布置参数 m

设置浮力调节量和滑块纵向位置调节量不变，浮力机构纵向布局和垂向布局的仿真轨迹和角度曲线如图8～图11所示。

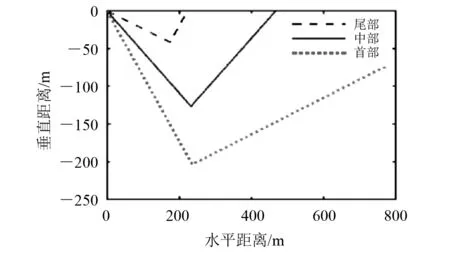
图8 纵向布局轨迹对比

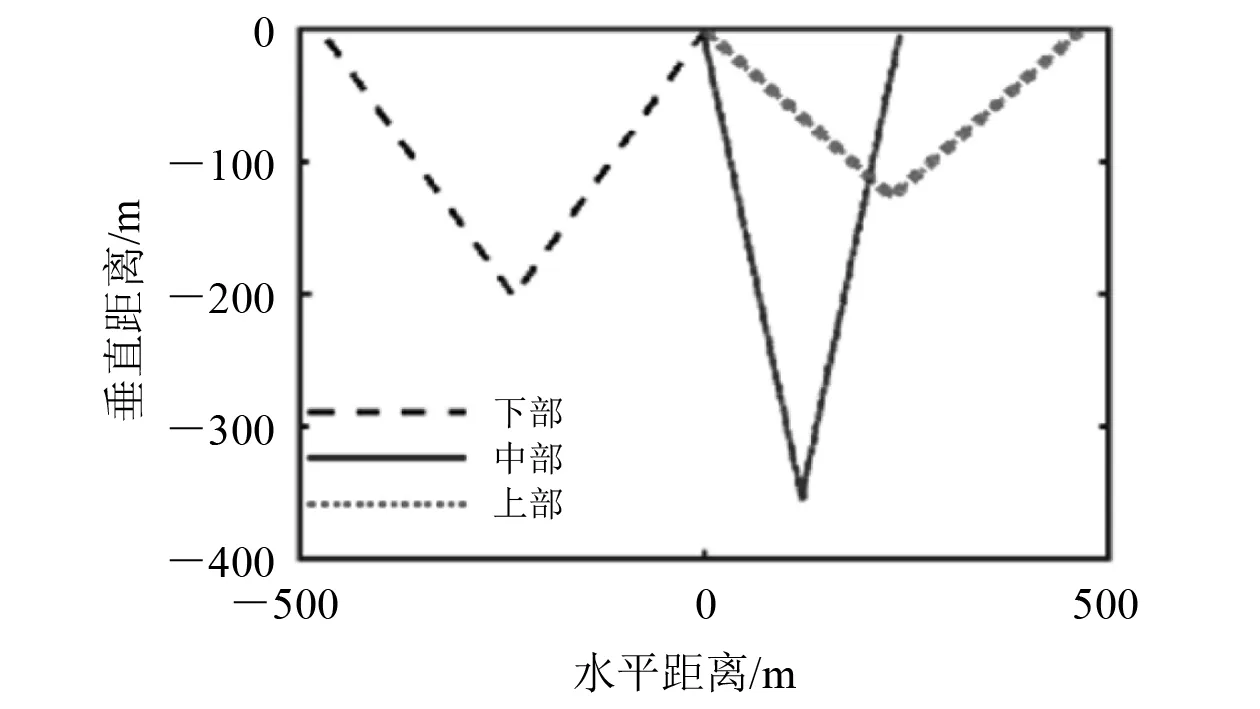
图9 垂向布局轨迹对比

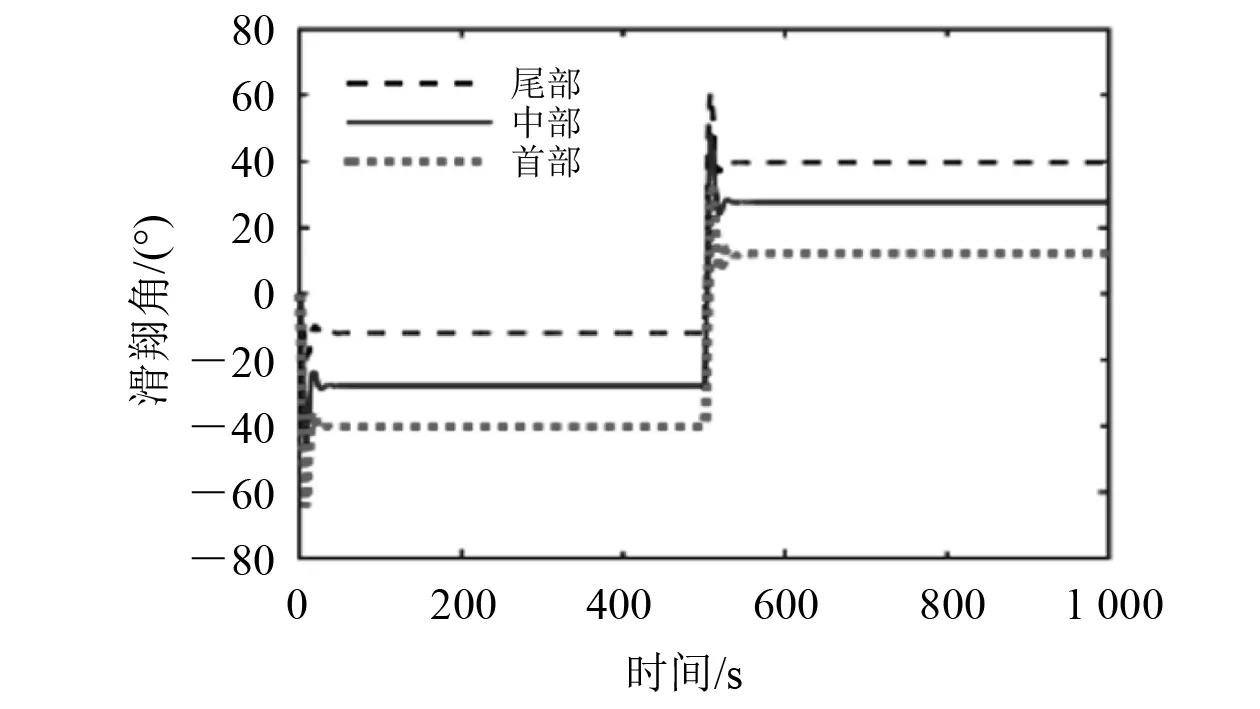
图10 纵向布局角度对比

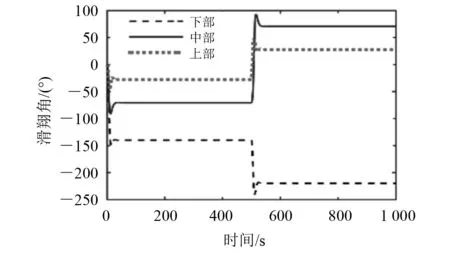
图11 垂向布局角度对比

图8表明：在执行机构调节相同量的条件下，纵向布局越靠近首部，水下滑翔机在一个运动周期内下潜的深度和滑翔的水平距离越大。这是由于浮力机构布置在首部会使水下滑翔机重心和浮心相对位置不在同一条直线上，进而会产生俯仰角力矩。如图10所示：俯仰角力矩在水下滑翔机下潜时起促进作用，使下潜滑翔角和下潜深度变大；俯仰角在上浮时起阻碍作用，使上浮滑翔角变小，从而滑翔更远的距离。

图9和图11表明：在执行机构调节相同量的条件下，浮力机构布置在下部，水下滑翔机会反向滑翔，事实上难以实现。由图10可得到浮力调节机构垂向位置rb3直接影响滑翔角的大小和方向：下方布局方式导致下潜和上浮时的俯仰角均为钝角；中部布局方式导致下潜和上浮时的滑翔角较大，下潜深度大但滑翔的水平距离小；上方布局方式导致下潜和上浮时的滑翔角较小，下潜深度小但滑翔的水平距离大。

综上所述，水下滑翔机在执行机构调节相同量时，浮力调节机构首部布置和上方布置方式在一个运动周期内，下潜相同深度可滑翔更远的距离，更有利于水下滑翔机在浅海水域的滑翔作业。

2.3 运动性能分析

(1)运动响应参数与系统输入关系

通过上述仿真，可得到水下滑翔机对油囊体积调节量和滑块纵向位置响应的定性关系，但是运动响应的角度和速度受何系统输入影响程度大、各自可达到的范围如何还需要进一步研究和分析。在Simulink仿真中设置的油囊体积调节量ΔV的调节范围为-0.001～0.001 m3,滑块纵向位置rp1的调节范围为-0.10～0.10 m。油囊体积调节量和滑块纵向位置的关系如图12～图15所示。

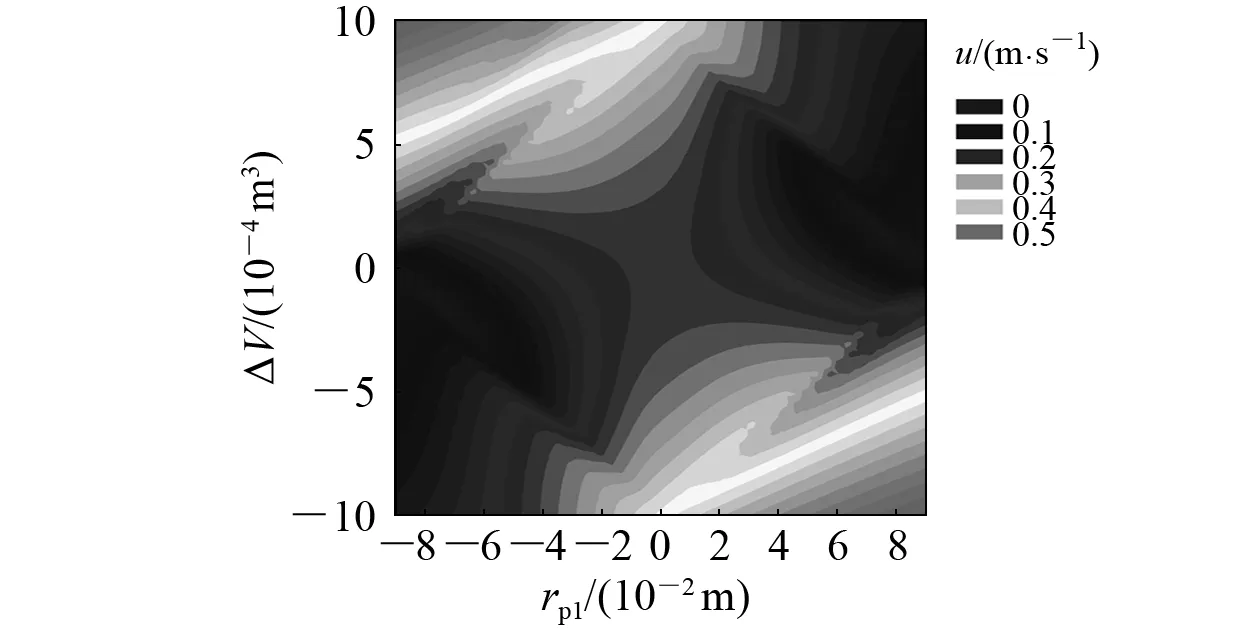
图12 水平速度变化

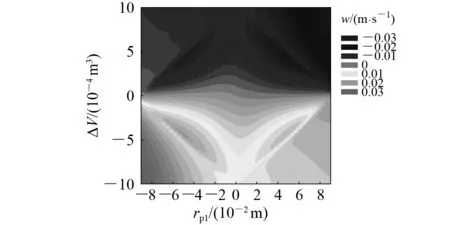
图13 垂直速度变化

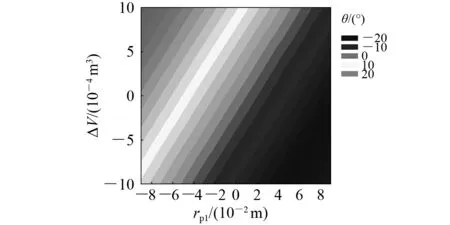
图14 俯仰角变化

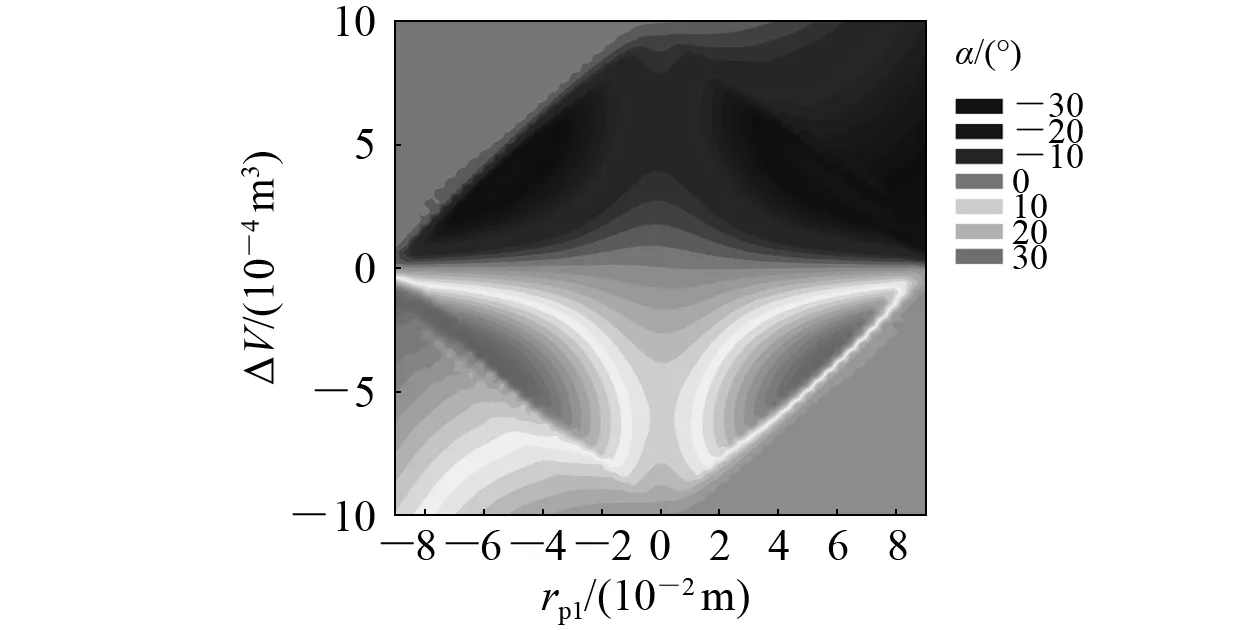
图15 攻角变化

由图12可知：在滑块纵向位置rp1=0时，水平速度u随着ΔV绝对值的增大而增大；在油囊体积调节量ΔV=0时，水平速度u随着rp1绝对值的增大而增大，但从水平速度的变化范围来看，ΔV对水平速度u的影响显著；但在ΔV绝对值靠近最大值时，rp1对水平速度影响显著。

由图13可知：在滑块纵向位置rp1=0时，垂直速度w随着ΔV绝对值的增大而增大；在油囊体积调节量ΔV=0时，垂直速度w随着rp1绝对值的增大而几乎不变，因此ΔV对垂直速度w的影响显著；但在ΔV绝对值靠近最大值时，rp1对水平速度影响显著，而且水平速度和垂直速度绝对值的最大值出现位置刚好相反。

由图14可知：在滑块纵向位置rp1=0时，俯仰角θ随着ΔV绝对值的增大而增大；在油囊体积调节量ΔV=0时，俯仰角θ随着rp1绝对值的增大而增大，但从θ的变化范围来看，rp1对俯仰角θ的影响更显著。

由图15可知：攻角α达到极值不是在滑块达到最大位移时，而是在滑块位移和油囊体积调节量ΔV均处于中间值时；从攻角α的变化范围来看，ΔV对攻角α的影响显著。

(2)滑翔比与角度之间关系

分析翼身融合水下滑翔机的滑翔比范围和相关物理量。通过仿真得到滑翔比与角度之间的关系，如图16和图17所示。

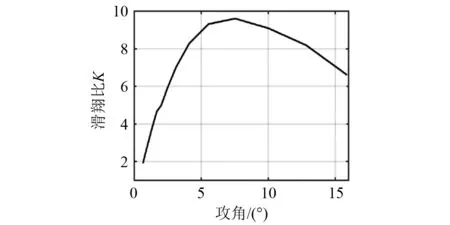
图16 滑翔比与攻角关系

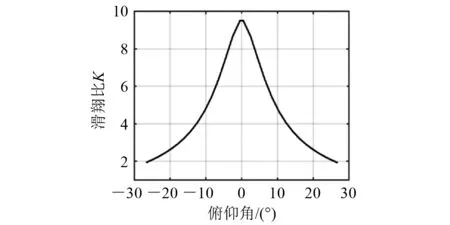
图17 滑翔比与俯仰角关系

结合图16和图17可知：翼身融合水下滑翔机的最大滑翔比可达9.6，滑行效率大幅高于传统的鱼雷型水下滑翔机，验证翼身融合水下滑翔机优异的水动力特性。

由图16可知：滑翔比随着攻角的增大先增大再减小，定义最大升阻比对应的攻角为有利攻角，从0°攻角到有利攻角，由于升力增加较快而阻力增加缓慢，因此升阻比增大；在攻角大于有利攻角时，升力增加缓慢，阻力急剧增大，因此升阻比减小。

由图17可知：滑翔比随着俯仰角绝对值越接近0°越大，由此可解释执行机构调节速度越慢水平滑翔距离越远的现象，这是因为调节速度越慢，水下滑翔机在俯仰角小角度区域过渡时间越长，可充分利用大滑翔比。

综合上述仿真分析，得到在油囊体积调节量ΔV取极值±0.001 m3、滑块纵向位置rp1调节范围为±0.10 m 时的翼身融合水下滑翔机运动参数范围，如表5所示。

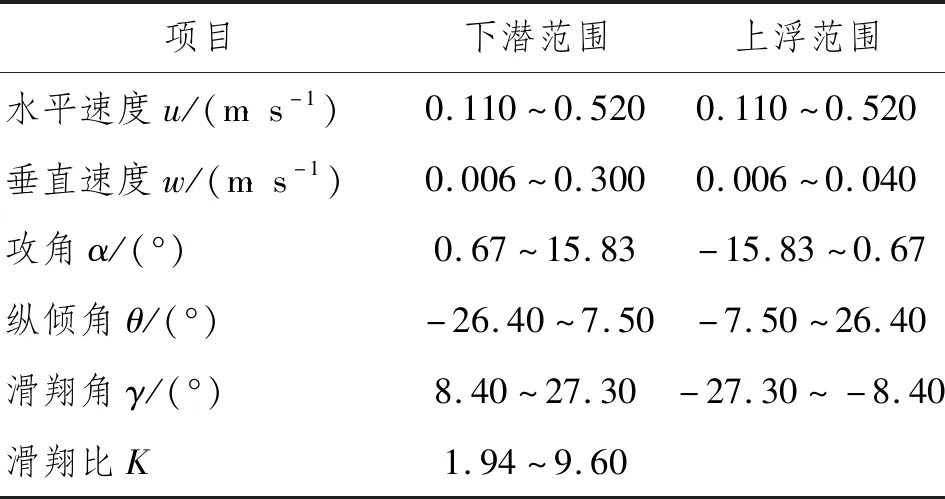
表5 翼身融合水下滑翔机运动参数范围

3 结 论

对翼身融合水下滑翔机三维模型进行动力学建模和开环运动响应仿真分析，同时对执行机构调节速度和浮力机构布置方式对运动性能的影响进行研究，分析水下滑翔机系统响应与输入之间的定量关系，归纳得到各运动参数的变化范围，得到如下结论：

(1) 执行机构阶跃调节和斜坡调节对翼身融合水下滑翔机角度和速度运动参数的平衡状态值大小无影响，只对其调节的暂态过程具有影响，调节速度快有利于快速性，调节速度慢有利于稳定性。

(2) 斜坡调节速度对轨迹的影响不明显，但随着调节速度的减小，水下滑翔机在一个完整运动周期内下潜深度减小，同时水平滑翔距离增大，有利于浅海水域滑翔作业。在执行机构调节量相同的条件下，浮力调节机构纵向布局在首部时，下潜和上浮的运动参数虽不再对称，但在下潜相同竖直距离时的水平滑翔距离更远；浮力调节机构垂向布局在上部时，在一个完整运动周期内，下潜深度小但滑翔的水平距离大：因此，首部和上部布局对于浅海水域滑翔作业具有实际指导意义。

(3) 滑块纵向位置rp1和油囊体积调节量ΔV对翼身融合水下滑翔机的角度和速度运动参数均具有影响，但综合来看油囊体积调节量ΔV对速度和攻角影响更显著，滑块纵向位置rp1对俯仰角贡献度更大。

(4) 滑翔比随着攻角的增大先增大后减小，随着俯仰角越接近0°越大，因此翼身融合水下滑翔机以较小的滑翔角度滑翔作业可充分利用小角度范围内大滑翔比的优势，增强浅海水域滑翔能力。