某些C*-代数的K-理论*
2022-07-19张惠莉刘树冬
曲阜师范大学学报(自然科学版) 2022年3期
张惠莉, 刘树冬
(①山东省创新发展研究院(山东信息通信技术研究院管理中心),250101,济南市;②曲阜师范大学数学科学学院,273165,山东省曲阜市)
0 引言及预备知识
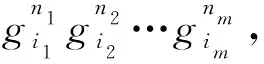


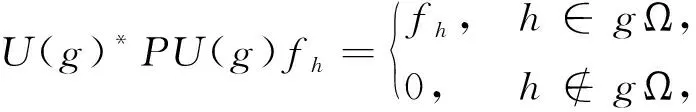
则U(g)*PU(g) 为l2(Γ) 到l2(gΩ) 上的投影,U(g)PU(g)*为l2(Γ) 到l2(g-1Ω) 上的投影.
令Tg=PU(g)P,称Tg是Toeplitz 算子,则




设A为 C*-代数. 若A≅A⊗K,则称A为稳定C*-代数,其中 K 为可分 Hilbert 空间上紧算子全体所成的 C*-代数.
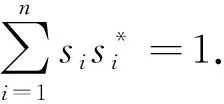

张爽证明了以下结论.
定理1[1](1) T+′=AP+′.
(2) 以下序列是正合的:0→K→T+′→On→0.
(3)RR(AP+′)=RR(IP+′)=0.

(2) IP+′是稳定的,且 IP+′/K≅On⊗K.
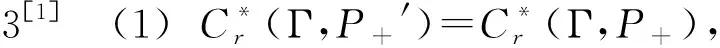
(2) T+=AP+且 AP+/K≅On.
本文主要计算这些C*-代数的K-群,所需的有关K-理论及 C*-代数扩张的知识可参考文献[2-10].
1 主要结果

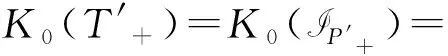

(2) 由于K0(En)=和K1(En)=0,由(1)知结论成立.


δ1↑↓δ0
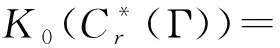
δ1↑↓δ0

0→→0和n→0,

由定理3,有以下结果.

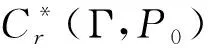

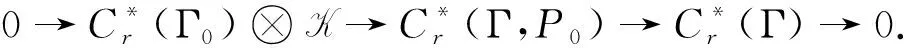
δ1↑↓δ0
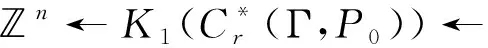
类似于定理4, 可以证明δ0=0和δ1=0,因此有以下两个正合列,
0→→0和n→0,

