全群 C*-代数的Haagerup 性质*
2022-07-19高昌源
高昌源, 孟 庆
(曲阜师范大学数学科学学院,273165,山东省曲阜市)
0 引 言
在群论和算子代数理论中,群的逼近性质与相对应的群 von Neumann 代数和群 C*-代数的逼近性质紧密相连. 这些逼近性质在几何、代数、遍历理论等领域有很多重要的应用,并被用于研究一些重要的数学猜想[1-4]. 群的 Haagerup 性质最早是 Haagerup[5]在研究非交换自由群时引入的,它是弱于顺从性的一种逼近性质.
定义1令G是一个离散群,如果存在G上正定函数组成的一个网{φi}i∈I满足φi(e)=1,且
(1) 对每个i∈I,φi在无穷远消失;
则称G有 Haagerup 性质.
在此之后,许多数学家都对这种性质做了研究,发现许多群都具有 Haagerup 性质[6-8]. 对于有限的 von Neumann 代数,同样可以定义 Haagerup 性质,Choda[9]证明了一个可数群有Haagerup 性质当且仅当它的群 von Neumann 代数有 Haagerup 性质. 与此类似,在文献[10]中董浙教授将 Haagerup 性质推广到有忠实迹态的单位 C*-代数的情形,并且证明了一个可数离散群有 Haagerup 性质当且仅当它的约化群 C*-代数有 Haagerup 性质. 最近,孟庆和王利广在文献[11] 中又定义了非单位 C*-代数关于权重的 Haagerup 性质,并进行了相应的研究.
本文在文献[11] 的基础上,研究离散群与其全群C*-代数的 Haagerup 性质之间的关系,证明了离散群有 Haagerup 性质当且仅当它的全群 C*-代数关于其上的经典迹态有 Haagerup 性质.
1 主要结果
在本文中,G是一个有单位元e的离散群,A是一个 C*-代数,τ是它的一个态,A+表示A的正元锥. 令Nτ={a∈A|τ(a*a)=0},Λτ(A)=A/Nτ,对任意的a,b∈A,定义内积
〈Λτ(a),Λτ(b)〉=τ(b*a),
则‖Λτ(a)‖2,τ=τ(a*a)1/2是相应的范数. 通过 GNS 构造,知道Λτ(A)关于‖·‖2,τ完备化得到一个 Hilbert 空间,记为L2(A,τ). 为了简化叙述,用 “c.p.” 表示完全正映射,“c.c.p.” 表示收缩的完全正映射和 “u.c.p.” 表示单位完全正映射.
若Φ:A→A是一个 c.c.p. 映射且满足τ∘Φ≤τ,那么由文献[11] 知,映射Λτ(a)|→Λτ(Φ(a)),a∈A可以延拓为L2(A,τ)上一个收缩映射,记为TΦ. 如果TΦ是L2(A,τ)上一个紧算子,则Φ是L2-紧的. 因此,通过 Hilbert 空间上紧算子与有限秩算子的关系,可以得到下面的引理.
引理1映射Φ是L2-紧的当且仅当对任意的ε>0,存在有限秩算子Q:Λτ(A)→Λτ(A)使得对任意的a∈A,
‖Λτ(Φ(a))-Q(Λτ(a))‖2,τ≤ε‖Λτ(a)‖2,τ.
证明首先注意这样一个事实:如果F是L2(A,τ)上一个有限秩算子,则存在xi,yi∈L2(A,τ),1≤i≤N使得
其中N是一个正整数.

所以存在xi,yi∈L2(A,τ),1≤i≤N使得
由于Λτ(A)在L2(A,τ)中稠密,故存在ai∈A使得
‖Λτ(ai)-xi‖2,τ≤ε/(2NM),
其中M=max{‖yi‖2,τ:i=1,…,N}. 令
那么Q是Λτ(A)上的有限秩算子. 对任意的a∈A,有
充分性. 由于Λτ(A)在L2(A,τ)中稠密,结论显然成立.
若B是A的一个稠密的*-子代数,那么Λτ(B)在Λτ(A)中稠密,从而在L2(A,τ)中稠密,因此通过与引理1同样的证明方法,我们可得下面的推论.
推论1若B是A的一个稠密*-子代数,那么Φ是L2-紧的当且仅当对任意的ε>0,存在有限秩算子Q:Λτ(B)→Λτ(B)使得对任意的b∈B,
‖Λτ(Φ(b))-Q(Λτ(b))‖2,τ≤ε‖Λτ(b)‖2,τ.
文献[11]给出了A关于权重(weight)的 Haagerup 性质的定义,由于A上的态显然是权重,因此有下面的定义.
定义2[11,定义3.2]令τ是A上的一个态. 如果存在A上的 c.c.p. 映射组成的网{Φi}i∈I满足
(1) 对任意的i∈I,τ∘Φi≤τ且每个Φi是L2-紧的;
(2) 在强算子拓扑下,{TΦi}i∈I收敛到恒等映射;
则称(A,τ)有 Haagerup 性质.
注1(1) 由文献[11] 可知,如果A是单位C*- 代数,上述 c.c.p. 映射可以被替换为 u.c.p. 映射.
(2) 定义2中的条件(2)等价于
‖Λτ(Φi(a))-Λτ(a)‖2,τ→0,a∈A.
下面介绍约化群C*-代数和全群C*-代数,详细内容参见文献[12]. 用[G]表示G的群环,它是由所有形如的元素组成的集合,其中只有有限多个ag∈不为 0. 在[G]中定义乘法和*运算如下:
‖x‖r=‖λ(x)‖B(2(G)),x∈[G]
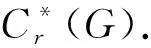
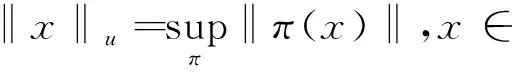
完备化后得到的C*- 代数为G的全群C*-代数,记为C*(G).显然对任意的x∈[G],‖x‖r≤‖x‖u,所以恒等映射I:[G]→[G]可以延拓为的经典*-同态ρ.从现在开始,令τ表示上的经典忠实迹态,即τ(x)=〈xδe,δe〉,其中{δg:g∈G}表示2(G)的经典标准正交基,那么τ′=τ∘ρ是C*(G)上的一个迹态.
下面给出群的 Haagerup 性质与它的群C*-代数的 Haagerup性质之间的关系. 为了方便,将G看成C*(G)的子集.
定理1若G是一个离散群,那么下列说法等价:
(1)G有Haagerup性质;
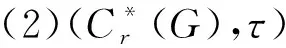
(3)(C*(G),τ′)有Haagerup性质.
证明(1)与(2)的等价性,在文献[10]中已证明,下面证明(1)与(3)等价.
(1)⟹(3). 假定G上的正定函数组成的网{φi}i∈I(φi(e)=1) 满足G有 Haagerup 性质的条件,定义相应的乘子mφi:[G]→[G]为
那么通过文献[12,定理2.5.11]知,mφi可延拓为C*(G)上一个u.c.p.映射,仍记为mφi. 接下来证明{mφi}i∈I满足(C*(G),τ′)有 Haagerup 性质的条件.

因此,对任意的x∈C*(G)+有τ′∘mφi(x)=τ′(x). 又
因为Λτ′([G])在L2(C*(G),τ′)中稠密,所以对任意的x∈C*(G),有
‖Λτ′(mφi(x)-x)‖2,τ′→0,(i→∞).
最后,证明每个mφi是L2-紧的. 对任意的ε>0,因为φi在无穷远消失,故存在一个有限子集Fi⊆G,使得当s∉Fi时,有|φi(s)|<ε. 定义Qi:Λτ′([G])→Λτ′([G])为
那么Qi是Λτ′([G])上良定义的有限秩算子. 另外
因此,由推论1知,对每个i∈I,mφi是L2-紧的.
(3)⟹(1). 若C*(G)上的 u.c.p. 映射组成的网{Φi}i∈I满足(C*(G),τ′)有 Haagerup 性质的条件,定义φi:G→为
φi(g)=τ′(g-1Φi(g)),g∈G,
那么
φi(e)=τ′(eΦi(e))=τ′(e)=τ(λe)=1.
因为TΦi是L2(C*(G),τ′)上的紧算子,当t→∞时,有
|φi(t)|=|τ′(t-1Φi(t))|=|〈Λτ′(Φi(t)),Λτ′(t)〉|≤
‖Λτ′(Φi(t))‖2,τ′=‖TΦi(Λτ′(t))‖2,τ′→0,
即φi在无穷远点消失. 另外,当i→∞时,
|φi(t)-1|=|〈Λτ′(Φi(t)),Λτ′(t)〉-1|=
|〈Λτ′(Φi(t)),Λτ′(t)〉-〈Λτ′(t),Λτ′(t)〉|=
|〈Λτ′(Φi(t)-t),Λτ′(t)〉|≤
‖Λτ′(Φi(t)-t)‖2,τ′→0.
最后,证明每个φi是正定的. 定义映射V:2(G)→2(G)⊗2(G)为V(δg)=δg⊗δg,则V是一个等距且对任意的b∈2(G)有V*(δg⊗b)=〈b,δg〉δg. 由 Fell 吸收原则[12]可知,存在一个*-同态使得σ(λg)=λg⊗g. 因为ρ∘Φi是的 c.p. 映射,所以通过文献[12] 知,是的 c.p. 映射,且满足
对任意的g,s∈G,有
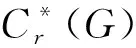
由文献[12,定理2.5.11] 知,φi是正定的.
最后,给出一个例子.
例1令2是由 2 个生成元生成的自由群,那么2有 Haagerup 性质[5]. 因此由定理1知,(C*(2),τ′)有 Haagerup 性质.
