多分辨分析的相似性*

李忠艳

(华北电力大学数理学院,102206,北京市)

0 引 言

设H=L2(). 令T和D是定义在H上的平移(酉)算子和扩张(酉)算子,即对任意f(t)∈L2(),

显然,TD=DT2.函数ψ∈L2()称作(单)正交小波如果}构成H的标准正交基.

设S⊂B(H),S的换位,记为S′,是指B(H)中所有与S中算子乘积运算满足交换律的算子集合,也即S′={A∈B(H)|AB=BA,∀B∈S}. {T}′是指平移算子T的换位.

定义1H的一个正交多分辨分析(MRA)M是指一列闭子空间{Vn:n∈}满足如下条件:

(1)Vn⊂Vn+1,∀n∈;

(3)DnV0=Vn,DVn=Vn+1,n∈;

(4)TV0=V0;

(5) 存在函数φ∈V0使得{Tφ=φ(x-l),∈,x∈}是V0的标准正交基.

条件(5)中的函数φ称作多分辨分析的(单)生成元或尺度函数. 多分辨分析(MRA)提供了一个构造新小波的自然的框架[1,2]. 文献[1]中一个著名的结果是由多分辨分析M构造正交小波ψ∈V1⊖V0.

设M={Vn,n∈}是一正交多分辨分析. 令φ是对应于M的尺度函数,ψ是由该多分辨分析构造的正交小波. 则由文献[2]知,小波子空间

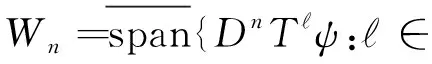
其中小波ψ∈W0.

关于子空间具有如下形式的分解

Wn⊕Vn=Vn+1,n∈和

因此集合{Tφ,DnT=ψ:n≥0,∈} 是H的标准正交基. 称 〈M,φ,ψ〉是一个MSW-三联组. 令MSW是所有MSW-三联组的集合. 记Pφ表示从空间H到空间V0上的正交投影,则有Pφψ=0和

套N是H中包含{0}和H的完备的闭(嵌套)子空间链. 套代数T(N)是包含所有将N中元素作为不变子空间的算子代数,也即套代数是包含了所有上三角形算子的集合. 令PN表示从H到N上的投影. 则

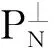
如果存在一个从套M到套N的双射θ,则称套M和N是序同构的. 如果该双射θ还满足

dimθ(M2)/θ(M1)=dimM2/M1, ∀M1⊂M2∈M,

则称θ是保持维数的序同构.

如果存在可逆算子S使得SM=N,则称套M和套N是相似的.

由定义1,将H的一个正交多分辨分析M扩充到M∪H,则这是一个完备的套,仍然记为M.以下无特殊说明,所有的多分辨分析都是这样扩充后得到的套. 我们称两个多分辨分析M={Mn,n∈}∪H和N={Vn,n∈}∪H是相似的是指如果存在可逆算子S使得SM=N.两个三联组〈M,φ0,ψ0〉和〈N,φ,ψ〉称作相似的,如果存在可逆算子S使得SM=N,Sφ0=φ,Sψ0=ψ.

关于正交多分辨分析小波集合W整体性质的研究,特别是拓扑性质——道路连通性的研究,在文献[3-5]中,作者证明了所有正交多分辨分析小波集合是道路连通的结果. 同时在文献[4,5]中,作者给出了所有正交多分辨分析的尺度函数集合也是道路连通的结论. 即在三联组集合MSW中,尚未作为整体集合性质讨论的只有多分辨分析集合 M. 关于它有趣的问题是:H的所有正交多分辨分析集合{Mj,j∈Λ}中任意两个是否是相似的? 任意两个三联组是否是相似的? 本文我们将回答这两个问题，同时还考察了多分辨分析M所生成的套代数T(M)的双模结构.

1 正交多分辨分析的局部换位与相似

设ψ是一正交小波,令

Cψ(D,T):={A∈B(H):ADnTψ=DnTAψ, ∀n,∈},

Uψ(D,T):={U:U是Cψ(D,T)中的酉算子}.

集合Cψ(D,T)称作算子对{D,T}在ψ的局部换位[6]. 令W(D,T)是H中所有正交小波集合. 设ψ0是W(D,T)中任意确定的正交小波,在文献[6]中证明了正交小波局部换位算子参数化的结果,即W(D,T)=Uψ0(D,T)ψ0的结论,且在Uψ0(D,T) 和 W(D,T)存在双射θ使得θ(U)=Uψ0.

称酉算子U将一个MSW-三联组〈M0,φ0,ψ0〉映射到MSW-三联组〈M,φ,ψ〉,如果

φ=Uφ0，ψ=Uψ0，V0′=UV0，Vn′=DnV0′,n∈，M={Vn′:n∈}.

记作〈M,φ,ψ〉:=U〈M0,φ0,ψ0〉.

对于一个MSW-三联组〈M0,φ0,ψ0〉, 定义

U(M0,φ0,ψ0):={U:U是C(M0,φ0,ψ0)中的酉算子}.

对于每一个MSW-三联〈M,φ,ψ〉,显然{D,T}′中的酉算子集合是U(M,φ,ψ)的子集.

利用正交小波的局部换位算子参数化的结果,在文献[7]给出了MSW-三联组集合MSW的如下算子参数化结果.

引理1[7]设〈M0,φ0,ψ0〉是一确定的MSW-三联组. 则由Γ(U)=U〈M0,φ0,ψ0〉定义的映射

Γ:U(M0,φ0,ψ0)→MSW

是双射.

定理1H中任意两个正交多分辨分析M和N是相似的.

证明假设由M={Vj,j∈}确定的MSW-三联是引理1中的〈M0,φ0,ψ0〉,N={Vj′,j∈}确定的MSW-三联是〈N,φ,ψ〉,它们对映的小波子空间分别记为Wj和Wj′. 由引理1知,存在酉算子U使得

〈N,φ,ψ〉=U〈M0,φ0,ψ0〉.

由于U∈C(M0,φ0,ψ0),UT=TU.又由于{Tnφ0:n∈}是V0的标准正交基, 所以

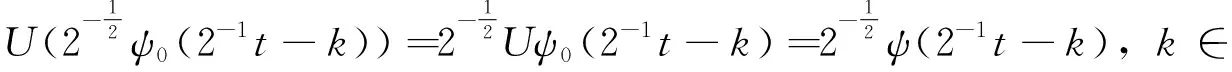
推论1三联组集合MSW中的任意两个MSW-三联组是相似的.

证明见定理1的证明.

注1由定理1的证明知,对于由多分辨分析M和多分辨分析N生成的套代数T(M)和套代数T(N),显然成立关系

UT(M)U*=T(UM)=T(N).

2 多生成元正交多分辨分析的局部换位与相似

H的r重多正交多分辨分析(r-MRA)M[8]是指一列闭子空间{Vn:n∈}满足定义1中条件(1)～(4),还满足如下条件:

(5′)存在函数向量

Φ(x)=(φ1(x),φ2(x),…,φr(x)),φi(x)∈L2(),i=1,2,…,r,

使得{Tnφj(x),j=1,2…,r,n∈}是V0的标准正交基, 其中Φ(x)称为r-重生成元,或r-重尺度函数.

由r-重多生成元正交多分辨分析可以构造r-重多正交小波Ψ(x)=(ψ1(x),ψ2(x),…,ψr(x)), 其中ψi(x)∈W0=V1⊖V0,i=1,2,…,r,使得{DnTψi,n,∈,i=1,2,…r}是L2()的标准正交基. 其中小波子空间,i=1,2,…,r},n∈.同样地有子空间分解关系

Wn⊕Vn=Vn+1,n∈;

因此,集合{Tφi,DnTψi:n≥0,∈,i=1,…,r}是H的标准正交基. 仍然用PΦ表示到子空间V0上的正交投影,则

设M是r-重多分辨分析，Φ=(φ1,…,φr)是对应的r-重尺度函数,Ψ=(ψ1,…,ψr)是由该多分辨分析生成的r-重多正交小波,称〈M,Φ,Ψ〉是一个r-MSW-三联组. 所有这样的r-MSW-三联组的集合记做r-MSW.

设Ψ是r-重多正交小波,算子{D,T}在Ψ的局部换位定义为

CΨ(D,T)={A∈B(H):ADnTΨ=DnTAΨ, ∀n,∈}=

{A∈B(H):ADnTψi=DnTAψi,i=1,…,r,∀n,∈}.

称酉算子U将一个r-MSW三联组〈M0,Φ0,Ψ0〉映射到r-MSW三联组〈M,Φ,Ψ〉,如果

Φ=UΦ0,i.e.φi=Uφ0i,i=1,2,…,r;

Ψ=UΨ0,i.e.ψi=Uψ0i,i=1,2,…,r;

V0′=UV0，Vn′=DnV0′,n∈，M={Vn′:n∈}.

记作〈M,φ,ψ〉:=U〈M0,Φ0,Ψ0〉.

设〈M0,Φ0,Ψ0〉是一个r-MSW三联组,定义

U(M0,Φ0,Ψ0):={U:U是C(M0,Φ0,Ψ0)中的酉算子},

其中UΨ0(D,T)是CΨ(D,T)中酉算子集合.

令Wr(D,T)是H中所有r-重多正交小波集合. 设Ψ0=(ψ01,…,ψ0r)是Wr(D,T)中任意确定的正交小波,在文献[9]中给出了r-重多正交小波局部换位算子参数化的结果,即Wr(D,T)=UΨ0(D,T)ψ0的结果,且在UΨ0(D,T) 和 Wr(D,T)存在双射θ使得θ(U)=UΨ0.利用该结果,在文献[10]中给出了r-MSW三联组集合r-MSW的算子参数化结果.

引理2[10]设〈M0,Φ0,Ψ0〉是一确定的r-MSW-三联组. 则由I(U)=U〈M0,Φ0,Ψ0〉定义的映射

I:U(M0,Φ0,Ψ0)→r-MSW

是双射.

由引理2,类似于定理1的证明,可得如下结果.

定理2H中任意两个r-重多生成元正交多分辨分析M和N是相似的.

推论2三联组集合r-MSW中的任意两个r-MSW-三联组是相似的.

3 正交多分辨分析生成套代数的双模

文献[11]详细刻画了抽象的所有类型的套生成套代数的双模结构,我们借助该文的讨论方法说明正交多分辨分析N作为Hilbert空间H=L2()特殊的套,算子代数B(H) 是关于套代数T(N)主范数双模的结论,该结果是文献[11]的特例.

设B1,B2⊂B(H)是子代数,且设A⊆B(H)是范数闭的线性子空间. 如果B2·A·B1⊆A,称A是一个B2(左)-B1(右)双模. 如果B1=B2=B,称A是一个B-双模. 如果存在一个元素G∈B(H)使得A=[B2·G·B1], 称A为主范数双模. 其中[·]表示线性范数闭包.

对于多分辨分析N={Nj,j∈}∪H,由所有从H到N上的投影算子生成的Von-Neumann 代数IN是B(H)的交换 Von-Neumann子代数.

令x是H中IN的可分标准(单位)向量. 定义映射Φ:N→[0,1]使得Φ(N)=〈PNx,x〉=‖PNx‖2.映射Φ是1-1的保持N中(包含)序的映射,其像集Φ(N)是[0,1]的紧子集,且包含点{0,1}. 这样的映射Φ不唯一,但是所有不同的这样映射的像集都是彼此序同构且同胚的. 称N中一个网{Nα}强算子拓扑收敛到N0∈N 当且仅当在[0,1]中Φ(Nα)→Φ(N0).也即此时将套N和正交投影套{PN}等同起来. 我们可以将N中的元素N用Φ(N)指标索引. 下面的记号形如N={Nλ:λ∈Λ⊂[0,1]}的套均指集合Λ是由这样一个指标映射的像集合. 如果Λ是一个无限集合,用α和β分别表示Λ的极小和极大极限点. 设λ1≤λ2,λ1,λ2∈Λ.记投影算子P=N[λ1,λ2]=PNλ2-PNλ1且K=PH.则N [λ1,λ2]={P(N):N∈N}是K的一个套. N[λ1,λ2] 称为N的区间套. 算子N[λ1,λ2]称作N-区间[11].

引理3 设N是Hilbert空间H=L2()的正交多分辨分析所构成的套,假设其包含一个无限子套N0={Nn,n∈}使得对所有的n∈,

dim(Nn+1-Nn)=dim(N1-N0),

且∩{Nn:n∈}={0}, ∪{Nn:n∈}=H.

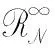
证明由于N={Nn,n∈}∪H是H的正交多分辨分析,令ψ是其对应的小波函数. 由于…⊂Nn-1⊂Nn⊂Nn+1⊂…, 则

且∩{Nn:n∈}={0}, ∪{Nn:n∈}=H.

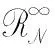
定理3 设N是H的任意正交多分辨分析,则B(H)是由其生成的套代数T(N)的主范数双模.

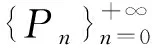
…⊂N-3⊂N-2⊂N-1⊂N0⊂N1⊂N2⊂N3⊂…,

…⊂P3⊂P2⊂P1⊂P0=Q0⊂Q1⊂Q2⊂Q3⊂….

由N的子空间的结构,则依照算子强拓扑，

limPn=0且dim(Pn-Pn+1)=+∞;

limQn=I且dim(Qn+1-Qn)=+∞,n∈∪{0}.

记En=Qn-Qn-1,n∈,且E-n=Pn-1-Pn,n∈.对于n∈{0}, 记Mn=∪{Ei:i≤n,i≠0}.令

M={Mn:n∈{0}}∪{0,IH}.

套M是PN的一个子套. 对于n∈{0}, 令Un是从支集子空间EnH(小波子空间)到像子空间E-nH(小波子空间)的部分等距算子. 定义

则U是酉算子. 现说明U就是双模生成元(见文献[11]命题3的证明). 对任意T∈B(H), 存在正的可逆算子{Ti}和复数{αi}使得

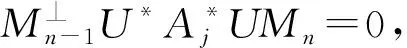
即B(H)=[T(N)·U·T(N)].