非线性不变性及相关矩阵方法在密码分析中的应用*

张文英, 孙晓萌, 雷 虹

(①山东师范大学信息科学与工程学院,250014,济南市;②东营职业学院,257091,山东省东营市)

0 引 言

密码学意义上的布尔函数相关矩阵[1]的概念由Joan Daemen在1993年召开的信息安全和密码会上提出，它从全局的角度揭示了布尔函数的内在性质，相关矩阵是刻画和理解线性密码分析的最天然的表示方法. 在2018年之前该方法主要用于做线性密码分析.

在2018年的亚密会上,比利时鲁汶大学的Tim Beyne把相关矩阵方法成功的用在对分组密码Midori和MANTIS-4的弱密钥攻击上，找到了 Midori的296个弱密钥,对MANTIS-4进行了密钥恢复攻击[2]. 其办法是找到轮函数中各个子函数—S盒，线性层和轮密钥加运算的相关矩阵， 寻找所有相关矩阵共同的特征向量,这里S盒和线性层的相关矩阵都是固定的，与密钥无关，而轮密钥加运算所对应的相关矩阵依赖于密钥， 其特征矩阵也依赖于密钥. 先求出S盒相关矩阵与线性层相关矩阵与特征值±1对应的共同的特征向量，再寻找让这些特征向量也是加密钥函数相关矩阵特征向量的条件，这个条件就是密钥应该满足的条件，即满足这些条件的密钥就是弱密钥. 各个子函数共同的特征向量在傅里叶变换的逆变换(反演公式)下对应的布尔函数就是密码不变函数g. 也就是明文和密文在该函数的作用下函数值之和是常数,即,对于不同的明密文对p1,c1和p2,c2,都有g(p1)+g(c1)=g(p2)+g(c2).如果把一轮加密函数的相关矩阵记作A,则A的特征向量一定是A2的特征向量,但是反之A2的特征向量不一定是A的特征向量. 于是可以寻找多轮加密的特征,例如,寻找向量u,v使得Au=v,Av=u,于是A2u=Av=u,如果这样的u对应的密钥空间大,则攻击效果更好. 如此便把密码分析问题转换成求密码函数所对应的相关矩阵的与特征值±1所对应的特征向量问题.

本文对相关矩阵方法在线性密码分析和弱密钥攻击中的应用进行综述，揭示问题的实质和所用方法数学依据，包括一轮密码变换下的密码不变性和连续多轮密码变换下的不变性. 本文的目的是让读者更深刻的理解密码不变性的数学实质，普及密码分析学知识.

1 预备知识

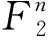
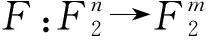
(1)

特别地，若m=1，则F(x)退化为布尔函数f(x)，此处若取v=1,通常记

称Sf(u)为布尔函数f(x)在点u的Walsh谱.

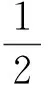
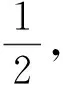
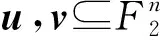
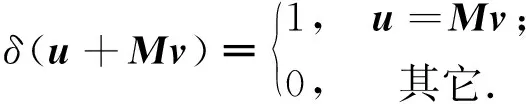
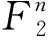
uh(x)T=(u1,…,un)(x1+k1,x2+k2,…,xn+kn)T=uxT+ukT，

则Ch(u,v)=(-1)ukTδ(u+v).

也就是说密钥加函数的相关矩阵是一个对角阵,对角元是Cu,u=(-1)ukT

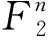
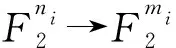
映射b=h(a)由各分映射bi=h(ai),0≤i≤l-1 确定. 每个S盒的相关矩阵Ci是2ni×2mi阶矩阵. 因为各hi的变量相互独立，各函数的输入变量之间无交集.h的相关矩阵可以如下计算,

(2)

本引理表明，对于多个小S盒并置得到的大型S盒，其相关矩阵就是各小型S盒相关矩阵的直积.

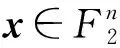
(3)

公式(3)和公式(1)的关系类似于傅里叶变换及其逆变换的关系,知道其中一方，可以求另一方.

如引言中所述，我们要求一个加密算法轮函数相关矩阵的特征向量，它对应着在加密变换下的一个不变量.首先介绍Midori分组密码算法.

2 Midori算法介绍及相关工作

2.1 Midori算法介绍

Midori是2015年亚洲密码会上提出的轻量密码,曾是当时加解密运算每比特能耗最少的算法. 为了达到低能耗的目的，算法使用了二元线性层，而非像以往使用MDS矩阵. Midori算法族含64比特分组和128比特分组两个版本,运行轮数分别是16和20. 两个版本分别记作:Midori64和Midori128. 明文和中间状态表示成4×4矩阵形式

对于Midori64和Midori128每单元分别为4比特和8比特. 因本文只分析Midori64，所以下面只介绍Midori64里的运算. 轮函数包含S盒、单元换位、列混合和加密钥.

1. 进S-盒:每个4比特单元分别进 4比特S-盒S4,其真值表请见表1.

表1 S4的真值表

2.单元换位(Shuffle Cell):像洗牌那样按照下列公式变换16个单元的位置

(S0,S1,…,S15)←(S0,S10,S5,S15,S14,S4,S11,S1,S9,S3,S12,S6,S7,S13,S2,S8).

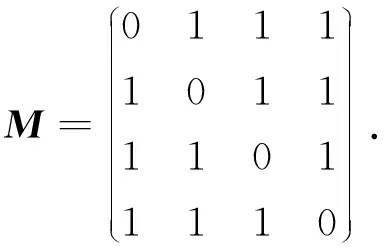
4. AddKey(AK)：模加轮密钥. 密钥K的长度为128比特，K的左半部分记为K0，右半部分记为K1,K=K0‖K1.K0⊕K1作为白化密钥，第i轮的轮密钥是Ki mod 2+αi,注意这里的轮常数αi是16维2元向量，例如α0=(0,0,1,0,0,1,0,0,0,0,1,1,1,1,1,1)，在与K0,K1模2加时，αi中的0或1以4比特2进制表示0000和0001呈现，所以K0,K1模加轮常数之后，其任何一个4比特单元的左侧3比特都保持不变，只有最低位比特可能改变. 16轮Midori 加密流程见图1.

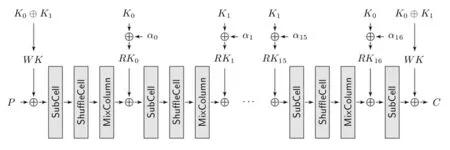
图1 16轮Midori 加密流程

2.2 Midori的 (非)线性不变性

对Midori算法的不变子空间攻击和非线性不变性攻击是弱密钥攻击的典型范例. 本小节介绍文献[3,6]中的工作. 如表1所示，郭建等发现8,9是Midori S盒的不动点，且在线性变换M下集合{8,9}映射到其自身，集合{8,9}中元素与轮常数0,1模加也还属于集合{8,9}，也就是每个单元只取8，9的明文在每个单元都只取0，或1的密钥加密下具有不变性，即：这样的密钥是是弱密钥.当明文的每个单元都只取8和9，用每个单元只取0和1的密钥加密时，密文的单元也只取8 或9. 表2 是用Midori64的弱密钥加密的例子.

表2 Midori特殊明文用弱密钥加密的结果

因为K0,K1各有16个单元，每个单元有0,1两种取法，这种形式的密钥共有232个[3].称这种方法为不变子空间攻击.

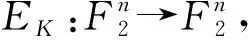
g(x)+g(EK(x))=ConstantK

(4)

的密钥K的个数尽量多，这里ConstantK表示只和密钥有关的函数，故可视为与明文无关的常数. 这种K称为弱密钥，称g为加密变换EK的非线性不变函数. 而对于一个随机函数，对于任意的明文，g(x)+g(EK(x))都等于同一常数的概率为2-n+1,利用公式(4),攻击者可以把弱密钥和普通密钥区分开来[6].令g(x)=x3x2+x2+x1+x0,Todo 等发现Midori 的S盒和线性层满足

g(x)=g(S(x)),

g(x)=g(Mx).

对于加轮密钥运算，由于

g(xk+k)=(x3+k3)(x2+k2)+x2+k2+x1+k1+x0+k0,

当k2=k3=0时，即密钥的每个单元的高2比特固定为0 时,

g(x)+g(x+k)=k1+k0,

g(x)在加密钥运算下具有不变性，于是若密钥的每个单元都只在集合{0,1,2,3}中取值时，g(P)+g(C)是只依赖密钥的常数. 因为K0有16个单元，每个单元有22种取法，共232种取法,K1也是如此，故这种弱密钥有264个[6]. 文献[6]用了非线性不变函数，得到了比文献[3] 更好的结果.

3 用相关矩阵方法寻找Midori的弱密钥

在文献[2]中，Tim提出了用加密运算相关矩阵的特征向量来描述非线性不变性，把对Midori 的弱密钥攻击推进了一步，可以找到296个弱密钥.

根据引理5，先求S盒，线性层和加密钥这三种变换的特征矩阵共同的特征向量. 为简单之计，仅仅计算4比特单元上各运算特征矩阵的特征向量，整个加密运算E是16 个单元上运算的并置，E的相关矩阵是16个矩阵的直积，特征向量也类似.

3.1 计算轮函数所有子函数的相关矩阵公共的特征向量

例1 对于Midori的S盒，根据公式(1)求出其相关矩阵如下

经计算，1对应的特征向量是 (1,0,0,…,0)T和(0,0,1,0,1,0,1,0,-1,0,-1,0,-1,0,-1,0)T以及二者的线性组合，-1对应的特征向量是 (0,1,0,0,0,1,0,0,0,-1,0,0,0,-1,0,-2)T和(0,0,0,1,0,0,0,1,0,0,0,-1,0,0,0,1)T以及二者的线性组合.

例2对于线性变换

(y3,y2,y1,y0)=(x1+x2+x3,x0+x2+x3,x0+x1+x3,x0+x1+x2),

其特征矩阵为

可以验证向量v=(0,0,0,1,0,0,0,1,0,0,0,-1,0,0,0,1)T是CM的属于特征值1的特征向量.

例3密钥加运算

(x3,x2,x1,x0)→(x3+k3,x2+k2,x1+k1,x0+k0),xi,ki∈F2

的相关矩阵CK为

CKv=(-1)k0+k1(0,0,0,1,0,0,0,(-1)k2,0,0,0,(-1)1+k3,0,0,0,(-1)k2+k3)T.

(5)

所以v是CK的特征向量当且仅当k2=k3=0. 对于加轮常数运算，由于Midori轮常数的每个单元都形如(0000),(0001),高位两比特都是0，所以满足了c2=c3=0 的要求.因为相关矩阵与函数一一对应，函数的复合运算对应着相关矩阵的乘积，v是矩阵CK,CM,CS共同的特征向量，那么也是它们乘积的特征向量，即若CSv=λ1v,CMv=λ2v,CKv=λ3v,则CKCMCSv=λ1λ2λ3v.所以，向量v是以上所有运算的复合运算的特征向量，即v是加密变换的特征矩阵的特征向量，相关矩阵为v的布尔函数是密码不变函数.v对应着那些每个单元高位两比特都是0的弱密钥，也就是文献[6]中那264个弱密钥.

例1中CS的和-1对应的特征向量

u=(0,1,0,0,0,1,0,0,0,-1,0,0,0,-1,0,-2)T+(0,0,0,1,0,0,0,1,0,0,0,-1,0,0,0,1)T=

(0,1,0,1,0,1,0,1,0,-1,0,-1,0,-1,0,-1)T

也是CM和CK的特征向量，且对应着k1=k2=k3=0 情形,也就是文献[3]里的那232个弱密钥.

3.2 相关矩阵的特征向量方法与文献中[3,6]方法的联系

把向量v单位化得到

如果把v1的第w个分量看成是某个布尔函数f在w的Sf(w)，那么根据反演公式(3)可以求出f在点x=0,1,2…,15 处的函数值(-1)f(0)=1,(-1)f(1)=-1,(-1)f(2)=-1,…,(-1)f(15)=1，用表格列举如下.

表3 f(x)的真值表

该函数的代数标准型ANF为f(x3,x2,x1,x0)=x3x2+x2+x1+x0,就是文献[6]函数中的非线性不变函数g.

3.3 方法的改进

求非线性不变函数的数学实质就是先找加密变换函数的相关矩阵的与±1对应的长度为1的特征向量e,再根据公式(3)求得的与e对应的布尔函数f，则此f必然满足f(P)+f(E(P))=c. 也就是明文和密文在加密函数的作用下，函数值的和是仅依赖于密钥的常数. 在3.2节中分别求出轮函数的各个子函数的相关矩阵的与特征值±1对应的共同的特征向量u，u对应的布尔函数便为密码不变函数，但是这样少统计了满足f(P)+f(E(P))=c的函数f的个数，因为根据公式(4)，u只需是加密变换相关矩阵的特征向量即可，不必是每个子函数相关矩阵的特征向量. 正如矩阵A和B的公共特征向量一定是AB的特征向量，但反过来，AB的特征向量不一定是A和B的公共的特征向量那样.也就是AB特征向量集合比A和B的公共的特征向量集合一般要大. 由于整个加密变换一般包含十几轮，多轮运算的复合运算也比较复杂，不易考察. 但是，我们可以考虑两轮变换的特征向量，而非只考虑一轮变换各个子函数共同的特征向量. 对于Midori64,若令y=(0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0)T,则当K0或K1的每个单元都有k2=k0=0时，就有

CKCMCSCKCMCSy=CKCMCSz=y.

也就是说虽然y不是一轮加密函数的相关矩阵的特征向量，但它是两轮加密函数的相关矩阵的特征向量， 自然是任意偶数轮加密变换的特征向量. 因为只对K0或K1有条件限制k2=k0=0，所以满足条件的密钥数量为264·232=296.y对应的线性函数是h(x3,x2,x1,x0)=x2+x0,在使用弱密钥加密时，任意的明密文对都满足

即明文和密文所有偶数下标的比特之和是只和所用密钥有关，与明文无关的常数.

4 结束语和说明

本文具体介绍了用来恢复分组密码加密算法弱密钥的不变子空间攻击和非线性不变攻击方法，及相关数学原理. 为使论文内容直观易懂，我们只以4比特单元上的S盒和线性运算为例对基本理论进行了阐述，实际上Midori64加密运算是在64维2元向量上进行的，轮函数的相关矩阵是264阶矩阵，特征向量是264维向量，本文把它分解为16个16阶矩阵的直积，只在每个16阶矩阵上讨论问题. 一些具体的轮函数相关矩阵的特征向量求解算法请参考文献[2]. 关于非线性不变攻击的最新成果请参见文献[7].