基于正交试验的楔形橡胶减振器三向刚度研究

孙 翌，李嘉炜，姜晓妍，黄 靖*，曾宪奎，鉴冉冉，胡旭风

（1.青岛科技大学 机电工程学院，山东 青岛 266061；2.青岛澳泰交通设备有限公司，山东 青岛 266109；3.青岛绿金源安全技术有限公司，山东 青岛 266021）

伴随科技的不断发展，橡胶减振器的发展得到人们越来越多的关注。现代工业复杂的工艺操作及多变的工作环境对橡胶减振器的适应性要求越来越高。楔形橡胶减振器通常应用在对横向、纵向、轴向3个方向刚度都有要求的场所。受橡胶材料三重非线性特点以及减振器受力情况复杂和多变等因素的影响[1]，目前对楔形橡胶减振器的三向刚度影响因素研究较少。本工作以一款动车组吊挂装置的楔形橡胶减振器为例，通过有限元分析软件对减振器进行建模和分析，研究减振器的不同参数对其三向刚度的影响，并根据实际工程中减振器的三向刚度确定各个参数的取值范围，为减振器的设计、生产和制造提供理论依据[2-4]。用轴向、纵向和横向刚度分别为1 100，500和50 kN·mm-1[5]，根据楔形橡胶减振器的安装方式和安装空间可以确定其外形尺寸。在符合力学性能要求的前提下，采用Solidwork软件对楔形橡胶减振器外形进行简化，得到其三维几何图形，如图1所示。

橡胶材料性能较为复杂，具有三重非线性的特点，对其压缩过程进行精确的研究存在困难。

1 模型的建立

1.1 楔形橡胶减振器的有限元模型

动车组吊挂装置的楔形橡胶减振器的许因此在许可范围内，本工作对楔形橡胶减振器的压缩行为进行适当简化：橡胶层在承受压力时总体体积不会发生变化，减振器中的钢板不会随着压缩的进行发生形变，钢板与橡胶层看成一个 整体[6]。

在Abaqus软件中建立楔形橡胶减振器的有限元模型，橡胶层采用Hyper58单元、钢板采用Solid45单元划分网格，不同材料边界通过粘合处理。楔形橡胶减振器的三维有限元网格划分模型如图2所示。

1.2 橡胶材料的本构模型

1.2.1 单轴压缩试验

鉴于楔形橡胶减振器构造复杂，橡胶材料采用天然橡胶作主体材料。选取橡胶材料邵尔A型硬度为其本构模型的试验变量，确定45，60和75度3个水平，通过单轴压缩试验结果构建橡胶材料的本构模型，橡胶材料的压缩应力-应变曲线如图3所示。

1.2.2 本构模型确立

采用Mooney-Rivlin本构模型，对于橡胶材料等不可压缩材料，它能够较好地拟合压缩应力-应变关系[7-8]。不可压缩橡胶材料的Mooney-Rivlin本构模型关系式为

式中，W为应变能密度，C1和C2为与交联结构等有关的材料参数，I1和I2为应变不变量。

对于橡胶材料单轴压缩试验，以λ1，λ2和λ3分别表示3个坐标轴方向的主伸长比，λ表示总伸长比，则λ1＝λ，λ2＝λ3＝1/λ1/2。橡胶材料主应力（σ1）与其λ1的关系为

式中，P为静压力。

单轴压缩试验确定C1和C2的基本公式为

将单轴压缩试验的橡胶材料的应力-应变数据进行线性回归计算，得出橡胶材料的Mooney-Rivlin本构模型参数C1和C2，结果如表1所示。

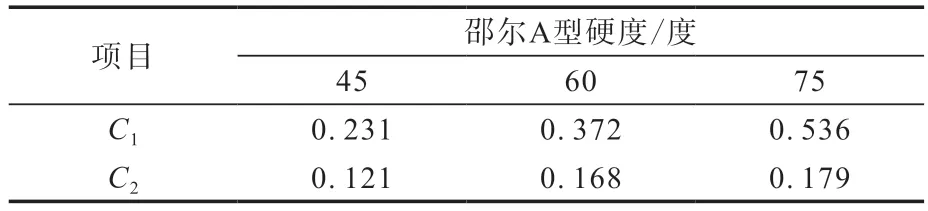
表1 3种邵尔A型硬度橡胶材料的本构模型参数值Tab.1 Constitutive model parameter values of three kinds of Shore A hardness rubber materials

对3种邵尔A型硬度橡胶材料进行有限元分析，将得到的压缩应力-应变曲线与试验曲线进行对比，如图4所示。

通过仿真与试验的压缩应力-应变曲线对比可以发现，Mooney-Rivlin本构模型满足本研究橡胶材料的有限元仿真要求。

2 正交试验及有限元分析

2.1 正交试验

采用L9（34）正交试验设计，选择橡胶材料邵尔A型硬度、橡胶层厚度、橡胶层倾斜角度和钢板数量作为变量因子，保证除变量因子外其他因素恒定进行正交试验[9-10]，正交试验因子与水平如表2所示，正交试验方案如表3所示。

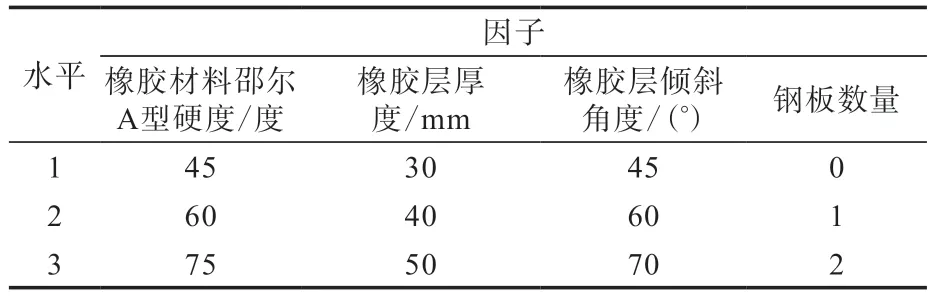
表2 正交试验因子与水平Tab.2 Factors and levels of orthogonal experiment

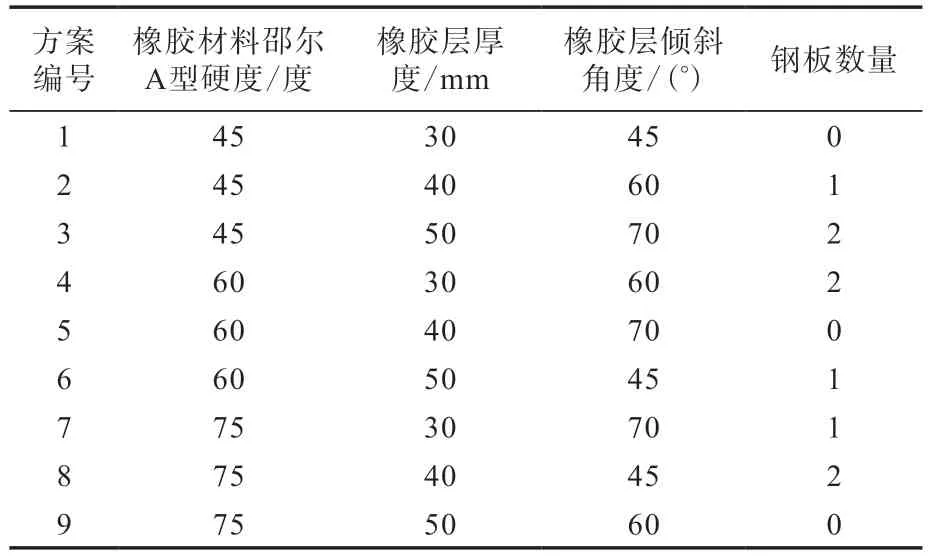
表3 正交试验方案Tab.3 Schemes of orthogonal experiment

2.2 有限元分析

楔形橡胶减振器钢板的弹性模量为206 000 MPa，而橡胶材料的弹性模量为7.8 MPa，其相比于钢板的弹性模量非常小[11]。因此，橡胶材料性质决定楔形橡胶减振器的静刚度大小。经过有限元分析，得到楔形橡胶减振器的三向刚度，见表4。

由表4可知，不同方案仿真结果之间存在明显差异，这说明变量因子对楔形橡胶减振器三向刚度的影响较为明显[12-15]。

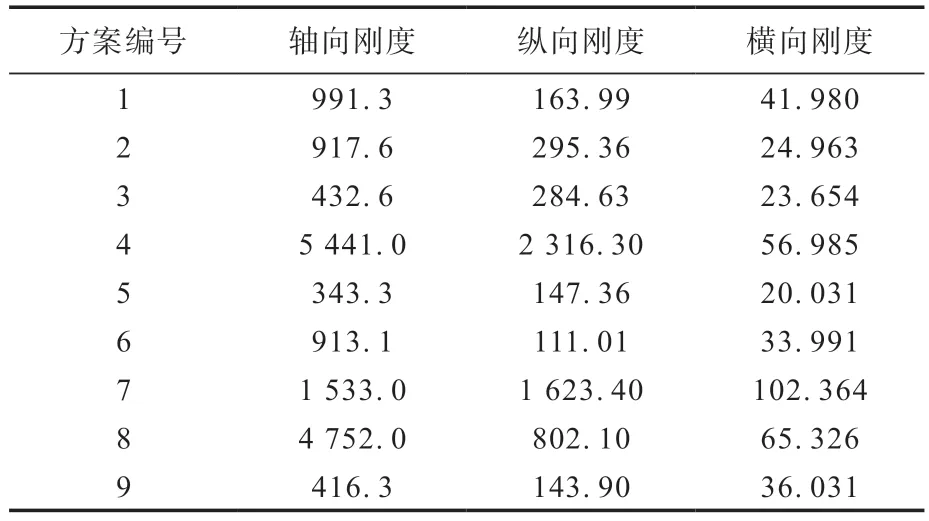
表4 楔形橡胶减振器的三向刚度有限元分析结果Tab.4 Finite element analysis results of three-dimensional stiffnesses of wedge-shaped rubber shock absorbers kN·mm-1

3 结果与讨论

3.1 橡胶材料邵尔A型硬度

橡胶材料邵尔A型硬度对楔形橡胶减振器三向刚度的影响如图5所示，轴向、纵向和横向刚度的拟合方程分别为式（4）—（6），相关因数均为1。

从图5可以看出，楔形橡胶减振器的轴向和纵向刚度随橡胶材料硬度的增大而逐渐增大，增大到一定程度后变化速度减缓甚至有减小的趋势，这是因为橡胶材料的弹性模量相对于金属材料非常小，橡胶材料性质决定减振器的刚度，通过增大橡胶材料硬度，可以快速增大减振器的刚度，但是当橡胶材料硬度达到一定水平后，其对减振器轴向和纵向刚度的影响作用减小。

从图5还可以看出，楔形橡胶减振器的横向刚度不同于轴向刚度和纵向刚度，在试验范围内变化不大，其随橡胶材料硬度的增大而略微增大。分析原因可能是减振器受轴向和纵向载荷时，橡胶材料均受到压缩与剪切双重作用，橡胶材料硬度对减振器轴向和纵向刚度的影响较为明显，但当其受横向载荷时，橡胶材料只受到剪切作用，而橡胶材料的抗压性能远强于抗剪切性能，因此橡胶材料硬度对减振器横向刚度的影响较小。

从图5还可以看出，同时满足楔形橡胶减振器三向许用刚度的橡胶材料邵尔A型硬度在66度 以上。

3.2 橡胶层厚度

橡胶层厚度对楔形橡胶减振器三向刚度的影响如图6所示。轴向、纵向和横向刚度的拟合方程分别为式（7）—（9），相关因数均为1。

从图6可以看出，随着橡胶层厚度的增大，楔形橡胶减振器的轴向和纵向刚度呈减小趋势，且减小幅度较大，横向刚度则略微减小。因为减振器的形变发生在橡胶层，随着橡胶层厚度的增大，减振器在受到载荷作用时形变增大，因此其三向刚度减小。但橡胶层厚度不能过小，否则将导致应力增大，造成减振器损坏；橡胶层厚度也不宜过大，橡胶材料的热导率小，过厚的橡胶层在振动生热时热量难以散失，会导致橡胶层过热损坏。

从图6还可以看出，同时满足楔形橡胶减振器三向许用刚度的橡胶层厚度为30～35 mm。

3.3 橡胶层倾斜角度

橡胶层倾斜角度对减振器三向刚度的影响如图7所示，轴向、纵向和横向刚度的拟合方程分别为式（10）—（12），相关因数均为1。

从图7可以看出，楔形橡胶减振器的轴向刚度受橡胶层倾斜角度的影响十分明显，当橡胶层倾斜角度大于55°时，减振器的轴向刚度随橡胶层倾斜角度的增大而急剧减小，这是因为随着橡胶层倾斜角度的增大，减振器受到的压缩作用减小、剪切作用增大，而橡胶材料的压缩模量远大于剪切模量，从而导致减振器的轴向刚度减小。同样，橡胶层倾斜角度对减振器横向刚度的影响很小，这是因为当减振器受横向载荷时，无论橡胶层倾斜角度多大，减振器只受到剪切作用。

从图7还可以看出，同时满足楔形橡胶减振器三向许用刚度的橡胶层倾斜角度为64°～67°。

3.4 钢板数量

钢板数量对楔形橡胶减振器三向刚度的影响如图8所示，轴向、纵向和横向刚度的拟合方程分别为式（13）—（15），相关因数均为1。

从图8可以看出，在试验范围内钢板数量多，楔形橡胶减振器的轴向和纵向刚度大。这是因为在橡胶层中增加钢板相当于间接减小了橡胶层厚度，使减振器承载后变形区的位移减小，减振器的静刚度增大。但如果钢板数量过多、橡胶层厚度过小，就无法满足减振器许用应力的要求。同时，钢板与橡胶层连接处最易发生疲劳断裂，钢板数量增多对减振器的使用寿命有较大影响。同样，钢板数量对减振器横向刚度的影响较小。

从图8还可以看出，同时满足楔形橡胶减振器三向许用刚度的钢板数量为1—2。

4 结论

采用有限元分析方法研究楔形橡胶减振器不同参数对其三向刚度的影响，得到如下结论。

（1）针对楔形橡胶减振器构造的复杂性，橡胶材料采用天然橡胶胶料，并以Mooney-Rivlin模型作为有限元分析的本构模型，单轴压缩仿真结果与试验结果吻合，证明所建本构模型满足有限元仿真要求。

（2）以橡胶材料邵尔A型硬度、橡胶层厚度、橡胶层倾斜角度和钢板数量为变量因子进行正交试验，对试验进行有限元分析，结果显示不同试验方案楔形橡胶减振器的三向刚度存在差异，说明变量因子对减振器性能的影响是明显的。

（3）橡胶材料邵尔A型硬度和橡胶层倾斜角度增大，楔形橡胶减振器的轴向和纵向刚度先增大后减小；橡胶层厚度增大，减振器的轴向和纵向刚度减小；钢板数量增多，减振器的轴向和纵向刚度增大；这4个变量因子对减振器的横向刚度影响 不大。

（4）同时满足楔形橡胶减振器三向许用刚度的橡胶材料邵尔A型硬度、橡胶层厚度、橡胶层倾斜角度和钢板数量分别为66度以上、30～35 mm、64°～67°、1—2。