基于反射系数估算的半空间边界阻抗和声源直接辐射重构*

周达仁 卢奂采 程相乐 McFarland D.Michael

(浙江工业大学机械工程学院,杭州 310023)

半空间中声源直接辐射声场重构的实施需要构造以边界声阻抗为参量的半空间基函数,边界声阻抗的获取则通常需要借助原位测量方法.基于半空间球面波基函数叠加的声场重构方法,通过在声源近场布置全息测量面和一支参考传声器采集声压,并以参考传声器声压重构误差取得最小值为准则,估算各全息测点的声压反射系数,就能在边界阻抗未知条件下实现声源直接辐射声压的重构,从而摆脱了常规方法对声阻抗原位测量技术的依赖.本文的目的是对这一方法进行详细的参数讨论,并在估算声压反射系数的基础上,进一步对边界声阻抗加以重构,提出一种基于近场声全息的声阻抗测量方法.以球形声源为例,对声阻抗和声源直接辐射声压的重构进行了仿真,定量地分析参考传声器坐标、边界有效流阻率和边界孔隙度随深度的降低率等参数对重构精度的影响.

1 引言

近场声全息[1]利用布置在振动结构近场的全息测量面采集声场信息,结合声场重构算法,可实现结构表面和三维空间中的声压、流体介质质点振速和声强等声学量分布的可视化,为结构声源的识别和定位提供技术支撑.近四十年来,傅里叶声学法[2]、逆边界元法[3]、球面波函数叠加法[4]和等效源法[5]等系列近场声全息方法的相继提出,标志着近场声全息在自由声场中的数学建模和工程实施已经形成较为成熟的理论体系.这些方法利用Helmholtz 方程的基本解,即自由空间格林函数建立结构表面声学量与空间场点声学量之间的关联,通过求解逆问题,将全息测量面上的声学量映射到重构面.然而,现实的测量环境通常不易满足理想的自由空间的要求.例如,对于潜艇等大型装备而言,其声辐射指标的测试通常只能在存在反射边界的船坞中进行,这使得测量值不可避免地受边界反射的影响,而不能真实反映声源的直接辐射量,更不能结合建立在自由空间中的近场声全息方法来实施声源直接辐射声场的重构.因此,研究含有反射边界的半空间中声源直接辐射声场重构的理论和方法,对于近场声全息进一步走向复杂环境下的工程应用具有重要意义.

半空间边界的声学特性可由声阻抗率表征.在工程环境中,边界声阻抗率的幅值一般为有限数值,这一类边界称作有限声阻抗边界或阻抗边界.参照近场声全息在自由空间的声场重构理论,在含阻抗边界的半空间中,若要实施声源直接辐射声场的重构,先要构造以边界阻抗为参量的、满足Helmholtz 方程和边界条件的半空间格林函数,建立半空间中场点声学量与声源表面声学量之间的关联.Zea 和Arteaga[6,7]参照傅里叶声学法,将半空间声压场表述为一组平面波基函数及其在边界处激发的反射波函数的叠加,提出了专门针对平面形状声源直接辐射声场的重构方法.Zhao 和Wu[8]将球面坐标系中的自由空间格林函数替换为半空间格林函数,参照逆边界元法,对半空间中振动结构表面的声学量进行了重构.Bi 等[9−11]参照等效源法,使用一组半空间格林函数的线性叠加来表述全息测量声压,通过求解半空间格林函数系数,实现半空间声学量的重构.Pan 等[12,13]将时域的半空间格林函数引入到等效源法中,对半空间瞬态声场进行了重构.

上述方法将边界阻抗作为参量分别引入傅里叶声学法、逆边界元法和等效源法的数学模型,建立半空间声场的数学模型和相应的声场重构算法.由此可知,声场重构的实施一般需要预先原位测得边界阻抗作为已知量.材料的声阻抗、声压反射系数和吸声系数等声学特性的原位测量技术[14],经过六十多年的发展,随着声场建模方案的不断优化和传感器技术的革新,而趋于多元化和精确化.其中,以近场声全息的数学模型为基础、结合传声器阵列作为前端的原位测量技术,因其相比于传统的双传声器法具有更强的抗测量噪声干扰的能力,而受到研究者的关注.Tamura[15]在声源和材料之间布置双层平面传声器阵列,基于傅里叶声学法,在波数域内分离出各波数分量的入射声压角谱和反射声压角谱,计算出材料的声压反射系数.Hald等[16]基于统计最优近场声全息法,使用双层平面传声器阵列采集声压信息,计算出材料的声阻抗、声压反射系数和吸声系数.Richard 和Fernandez-Grande[17]使用等效源法,结合球面传声器阵列作为测量前端,重构出材料表面的声压和质点振速分布,进而计算出声阻抗和吸声系数.Dupont 等[18]基于球面近场声全息的数学模型,使用球面传声器阵列作为测量前端,同样是通过重构材料表面的声压和质点振速分布,而得到声阻抗和吸声系数.总之,由于近场声全息具有对声学量重构的强大能力,将其应用于材料声学特性的建模与原位测量,是一条高效的解决途径.

近期,Zhou 等[19,20]参照球面波函数叠加法,将半空间声压场表述为一组半空间球面波基函数的线性叠加,通过求解基函数的系数,获取声源在自由空间中辐射声压场的基函数系数,进而实现含阻抗边界半空间中声源直接辐射声场的重构.Zhou 等[20]进一步提出,在全息测量面的一侧设置一支参考传声器,并定义全息测量面的声压反射系数均值,以参考传声器所在位置的声压重构误差为最小为原则估算出反射系数均值,就可以近似计算半空间球面波函数.从而,在边界阻抗未知的情况下,也可以实现声源直接辐射声场的重构.

适用于边界阻抗为未知量的声场重构方法,不再需要在现场布置标准声源和特定分布的传感器来预先测量边界阻抗,摆脱了常规方法对声阻抗原位测量技术的依赖,从而在很大程度上提高了工程实施效率.然而,现有的研究仅对该方法在一种阻抗参数条件下的声压重构进行了初步的仿真和实验验证,参考传声器坐标和边界阻抗等参数的变化对声压反射系数均值计算和声压重构误差的影响机理尚未得到研究.因此,本文将系统地考察该方法在不同参考传声器坐标和边界参数条件下,对声源直接辐射声压的重构精度;同时在估算声压反射系数均值的基础上,重构边界的声阻抗率,为声阻抗的原位测量提供一种基于近场声全息的解决方案.

2 数学模型

2.1 基于半空间球面波基函数叠加的声场重构理论基础

在含阻抗边界的半空间中,如图1 所示,声源几何中心O1到边界距离记为hs,以O1在边界的投影O为原点建立全局坐标系,其中,O1的全局坐标为xO1(0,0,hs).那么,声源在半空间中任一场点x的稳态声压响应phalf(x;ω) 为声源直接辐射与边界反射贡献的总声压,可以用不同阶次的半空间球面波基函数的线性叠加来表述[20]:

图1 半空间声场示意图 (a)声源、传声器阵列和阻抗边界的布置;(b)声源几何中心及其关于边界的镜像点与场点、阻抗边界之间的几何关系Fig.1.Schematic of the half-space sound field:(a) Setup of the source,the microphone array and the impedance boundary;(b) geometric relationship between the geometric center of the source,the mirror point,the field point and the impedance boundary.

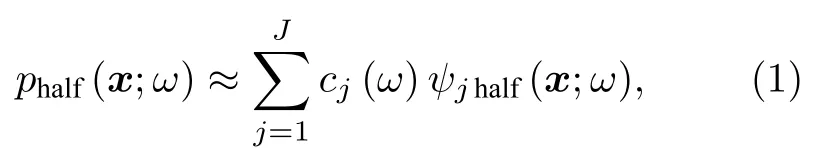
其中,ψjhalf(x;ω) 为满足Helmholtz 方程和阻抗边界条件的半空间球面波基函数[19,20],ω为声波角频率,j为基函数展开项序数,J为基函数展开项项数;cj(ω)为待求解的基函数展开项系数.

分别以O1及其关于边界的镜像点O2为坐标原点建立局部坐标系,场点x在两局部坐标系中的坐标分别记为x1≡(r1,θ1,ϕ1) 和x2≡(r2,θ2,ϕ2),它们与全局坐标x之间的关系为

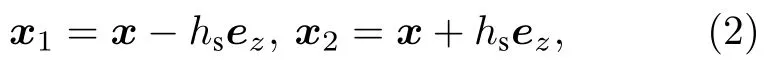
其中,ez为z向单位向量.利用两组局部坐标,ψjhalf(x;ω)可以表示为[20]

其中,ψj(x|x−hsez;ω) 为表述声源直接辐射的第j项球面波函数,ψj(x|x+hsez;ω) 为表述镜像虚源辐射的第j项球面波函数;Rp(θ2;ω) 为声压反射系数.

球面波函数在球面坐标系中的表达式为[4]

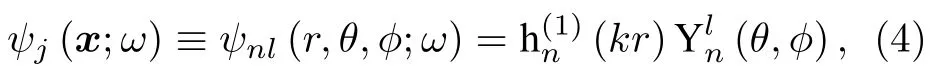
声压反射系数Rp(θ2;ω) 的表达式为[21]

式中,β为归一化的边界声导纳,

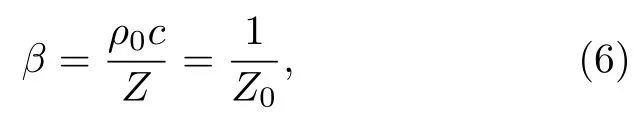
其中,Z为边界声阻抗率,ρ0为半空间流体介质密度,c为声速,Z0为归一化的边界声阻抗率.注意到,(5)式与平面入射波在边界的声压反射系数形式相同,所以(3)式右边的第2 项对反射声场的表述是近似解.随着场点与边界之间距离的增大,且大于半个声波波长时,场点接收到的反射波趋近于平面波,(3)式趋于精确解[21].另外,当边界声阻抗率逐渐增大,阻抗边界向完全刚性边界转变时,半空间任意场点的反射系数均逐渐趋近于1,此时,(3)式也趋于精确解.

如图1(a)所示,布置传声器阵列作为全息测量面,根据(1)式,可以得到如下线性方程组:

其中,上标†表示对矩阵求伪逆:

其中,上标H 表示矩阵的共轭转置.

当(7)式的系数向量{C(ω)}J×1确定之后,在半空间或者声源表面的任意场点处,半空间总声压和声源直接辐射声压可由如下两式重构:

2.2 边界阻抗和声源直接辐射声压的重构

由(3)式、(5)式和(6)式可知,半空间球面波函数以边界阻抗和场点坐标作为参量,因此,当边界阻抗未知时,为了计算各全息测点的半空间球面波函数,首先需要对各测点的声压反射系数进行估算.

对于具有有限声阻抗的物理边界而言,测点的声压反射系数为有界函数,满足如下关系:

2)建立如图2 所示的直角坐标系,其中,横轴和纵轴分别为Rp的实部Re[Rp] 和虚部Im[Rp].以坐标原点为中心画单位圆,对圆内区域划分网格,设置横轴和纵轴方向的网格步长各为∆x和∆y.由第τ个网格节点的坐标可确定反射系数Rpτ,作为的备选值,其中,τ1,2,···,T,T为节点总数.

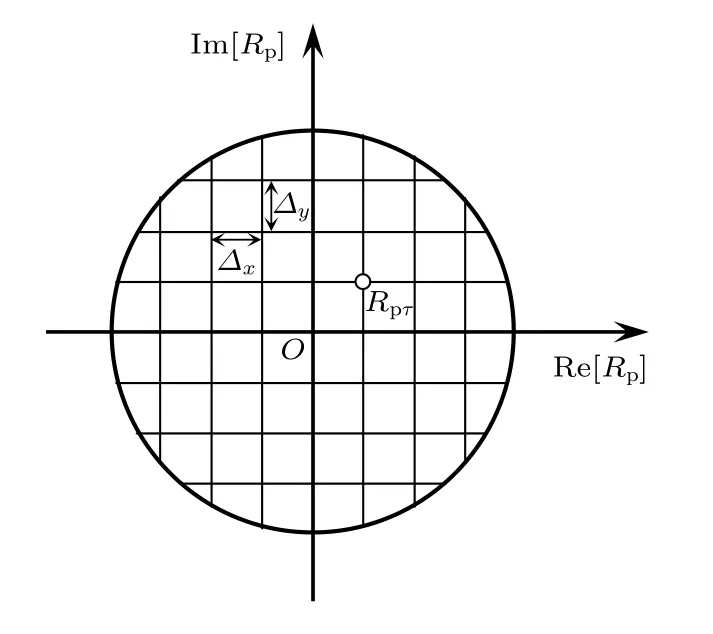
图2 单位圆内部区域的网格划分Fig.2.Mesh of the region inside the unit circle.

3)设定基函数展开项数J的取值上限为Jmax.将基函数展开项数和反射系数均值的一组备选值(J,Rpτ)赋给(7)—(10)式,再以全息声压值作为输入,重构参考测点处的半空间总声压并计算重构值与测量值的相对误差E:

如此遍历 (J,Rpτ)的所有备选值,将E取得最小值Emin时所对应的反射系数确定为反射系数均值.

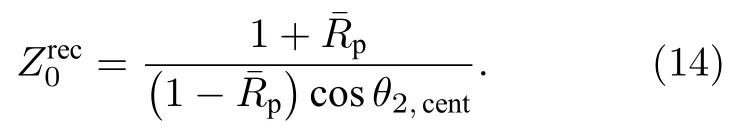
3 数值仿真验证

对脉动球声源和阻抗边界构成的半空间声场进行仿真.脉动球、传声器阵列、参考传声器和阻抗边界的布置如图3(a)所示.脉动球半径a0.05 m,表面振动速度V00.01 m/s ,球心O1距离阻抗边界hs0.30 m.传声器阵列为平面阵列,孔径为0.15 m×0.15 m,其上均布 6×6 个声压测点,相邻测点间距为0.03 m.阵列面与阻抗边界平行,两者距离ha0.20 m.声源和阵列面的几何中心均位于z轴.阵列测点的编号如图3(b)所示,其中,第1 号测点坐标为 (−0.075 m,0.075 m,0.200 m),第36 号测点坐标为 (0.075 m,−0.075 m,0.200 m).参考传声器坐标设为xref(0,0,0.05 m).假定阻抗边界坐标为z0,其表面声阻抗率满足声阻抗模型[22]:

图3 仿真声场示意图 (a)脉动球声源、传声器阵列、参考传声器和阻抗边界的布置;(b)阵列上传声器的编号Fig.3.Schematic of the simulated sound field:(a) Setup of the dilating sphere source,the microphone array,the reference microphone and the impedance boundary;(b) the indices of the microphones mounted on the array.

其中,σe为边界有效流阻率,αe为边界孔隙度随边界深度的降低率,f为声波频率.选取参数σe和αe的值分别为38kPa·s/m2和15m−1.空气介质密度ρ01.20 kg/m3,声速c343m/s.在仿真计算中,根据脉动球声源在自由空间中的辐射声压场和在半空间中激励的声压场的解析表达式[20],得到声源直接辐射声压的理论值和传声器测量的半空间总声压值.考虑传声器测量误差的影响,对传声器阵列和参考传声器测得的半空间总声压值附加信噪比为30 dB 的高斯白噪声.

为了对声阻抗率和声源直接辐射声压重构精度进行定量分析,定义声阻抗率的重构值与理论值Z0之间的相对误差为

定义声源直接辐射声压重构值与理论值之间的相对误差为

首先给出频率f1700 Hz 工况下,声阻抗率和声源直接辐射声压重构的结果.当频率f1700 Hz时,由(15)式给定的边界声阻抗率为Z02.06+2.23i,再根据(5)式和(6)式,可得位于全息测量面的场点声压反射系数Rp(θ2;ω) 的变化范围为0.565 ≤Re[Rp]≤0.573,0.311 ≤Im[Rp]≤0.315.这表明,在本算例所设定的声场参数条件下,全息测量面的场点声压反射系数随着θ2的变化,在很小的范围内波动.

设定网格步长为∆x∆y0.01,基函数展开项数取值上限为Jmax4 ,计算反射系数均值当基函数展开项数J1 时,参考测点的半空间总声压重构的相对误差取得最小值Emin0.75%,求得反射系数均值0.57+0.33i.

图4(a)所示为当J1 时,参考测点的总声压重构的相对误差E随反射系数Rp变化的三维曲面分布.从图4(a)可知,曲面上存在唯一的极小值点0.57+0.33i;并且,随着Rp与之间的距离的增大,E逐渐增大.当展开项数J取2,3 和4 时,也能得到与图4(a)所示相似的图像.这表明,总是存在一个反射系数均值,使得基于半空间球面波函数叠加的数学模型对阵列测点和参考测点的半空间总声压同时具有最高的描述精度.因此,以参考测点的总声压重构的相对误差取得最小值为准则,来求取反射系数均值是可行的.图4(b)所示为阵列测点的声源直接辐射声压重构的相对误差εpres随反射系数均值变化的三维曲面分布,其中,基函数展开项数J1.与图4(a)相似,图4(b)中也存在着唯一的极小值点0.58+0.33i;随着与之间距离的增大,εpres呈增大趋势.图4(b)表明,总是存在一个反射系数均值,使得基于半空间球面波函数叠加的数学模型对阵列测点的半空间总声压和声源直接辐射声压同时具有最高的描述精度.从而,以反射系数均值近似阵列测点的声压反射系数,对半空间总声压场进行建模,能实现对声源直接辐射声压的精确重构.当求得的越逼近其最优值时,声源直接辐射声压重构的精度越高.为了使尽可能地逼近,则需要通过合理地设置参考传声器的坐标来实现.

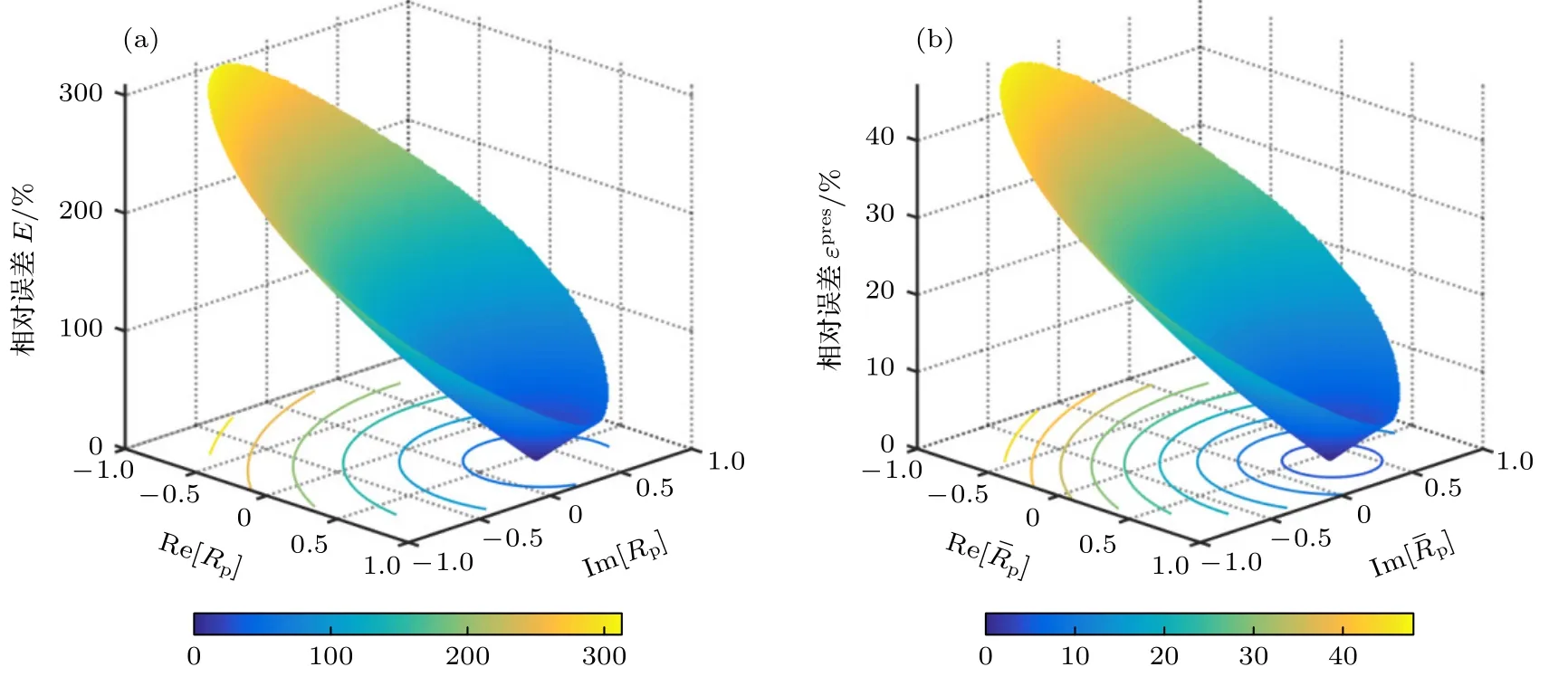
图4 相对误差的曲面图 (a)误差E 随反射系数 Rp变化的分布;(b)误差 εpres随反射系数均值 变化的分布Fig.4.Surface plot of the relative error:(a) The error E versus reflection coefficient Rp;(b) the error εpres versus mean value of the reflection coefficient .

在求得反射系数均值之后,令xcent(0,0,0.20 m),θ2,cent0,利用(14)式和(16)式,得到声阻抗率重构值为1.93+2.25i,重构值与理论值之间的相对误差为εimp4.41 %.

利用(7)—(9)式和(11)式,重构出阵列各测点处声源的直接辐射声压响应.图5 为无量纲声压幅值|p/(ρ0cV0)|在阵列测点的分布曲线,包括半空间总声压值、声源直接辐射声压的重构值和理论值.从图5 可见,半空间总声压值相对于声源直接辐射声压理论值存在明显的偏差,说明传声器阵列测得的总声压被边界反射污染,完全不能反映声源真实的直接辐射量.而在声场重构之后,声源直接辐射声压重构值与理论值的分布曲线能够很好地吻合.在本工况下,声压重构的相对误差为εpres0.29%.结果表明,该方法能以较高的精度抑制阻抗边界反射的影响,重构脉动球声源直接辐射的声压场,也能较为精确地重构边界声阻抗率.

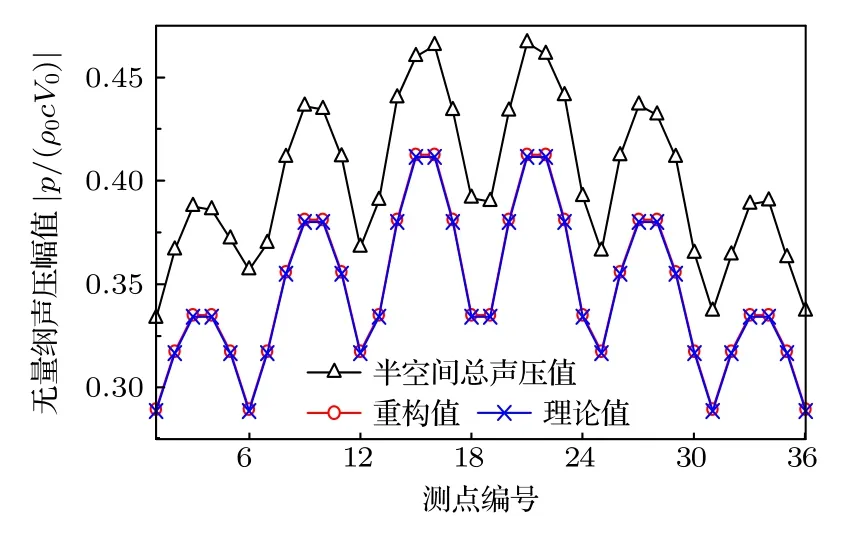
图5 半空间总声压、声源直接辐射声压的重构值和声源直接辐射声压的理论值在阵列测点的分布Fig.5.Sound pressure distributions at the measurement points on the array,including the total values in the halfspace,the reconstructed values and the benchmark values radiated directly from the source.

进一步,对频率f=100—3300 Hz 范围内的其他工况进行考察,得到如图6 所示的相对误差εimp和εpres随频率f的变化曲线.图6 显示,对于多数频率工况,εimp均保持在25%以下,表明本方法具有一定的对声阻抗率的重构精度;仅在f=100 和300 Hz 两个低频工况下,εimp>60%,这是因为在低频条件下,声波波长较长,使得阵列接收到的反射声波偏离假定的平面波模型较远.εpres在整个频率范围内保持在2.5%以下,且在大多数频率工况保持在1.5%以下,表明本方法具有较高且稳定的对声源直接辐射声压的重构精度.图6 所示的两条误差曲线随频率的变化趋势具有一定的相似性,这是因为声阻抗率和声源直接辐射声压重构的精度均依赖于声压反射系数均值与其最优值的逼近程度.需要说明的是,对于多数频率工况,图6 所示结果并非本方法所能取得的最小误差,因为参考传声器坐标的设置会对重构精度产生较大影响.

图6 声阻抗率重构的相对误差 εimp 和声源直接辐射声压重构的相对误差 εpres 随频率f 的变化曲线Fig.6.Relative error of the reconstructed specific acoustic impedance εimp and the relative error of the reconstructed sound pressure εpres radiated directly from the source versus frequency f.

4 参数讨论

本节考察参考传声器坐标以及边界有效流阻率、边界孔隙度随深度的降低率等参数对声阻抗率和声源直接辐射声压重构精度的影响.仿真声场的布置如图3(a)所示,声源、传声器阵列和阻抗边界的相关参数,以及测量信号信噪比和网格划分步长等参数的初始值与第3 节一致.参数讨论遵循单一变量的原则,即当考察某一参数的变化对重构精度的影响时,其他参数保持不变.

4.1 参考传声器坐标

首先考察参考传声器坐标xref的变化对边界声阻抗率和声源直接辐射声压重构精度的影响.注意到,在图3(a)所示的声场布置中,球声源的几何中心正对着全息测量面的几何中心,两者均位于z轴,使得全息测量面接收到的声能量主要集中在入射角为0 的方向.因此,为了充分获取该方向的声场信息,将参考传声器置于z轴,其坐标记为xref(0,0,zref).考察zref的变化所导致的声阻抗率重构的相对误差εimp和声源直接辐射声压重构的相对误差εpres的变化,考察范围为zref=0—0.19 m.当频率f100 Hz,900 Hz,1700 Hz,2500 Hz和3300 Hz时,使用本方法所得到的εimp和εpres曲线分别如图7(a)—(e)所示.

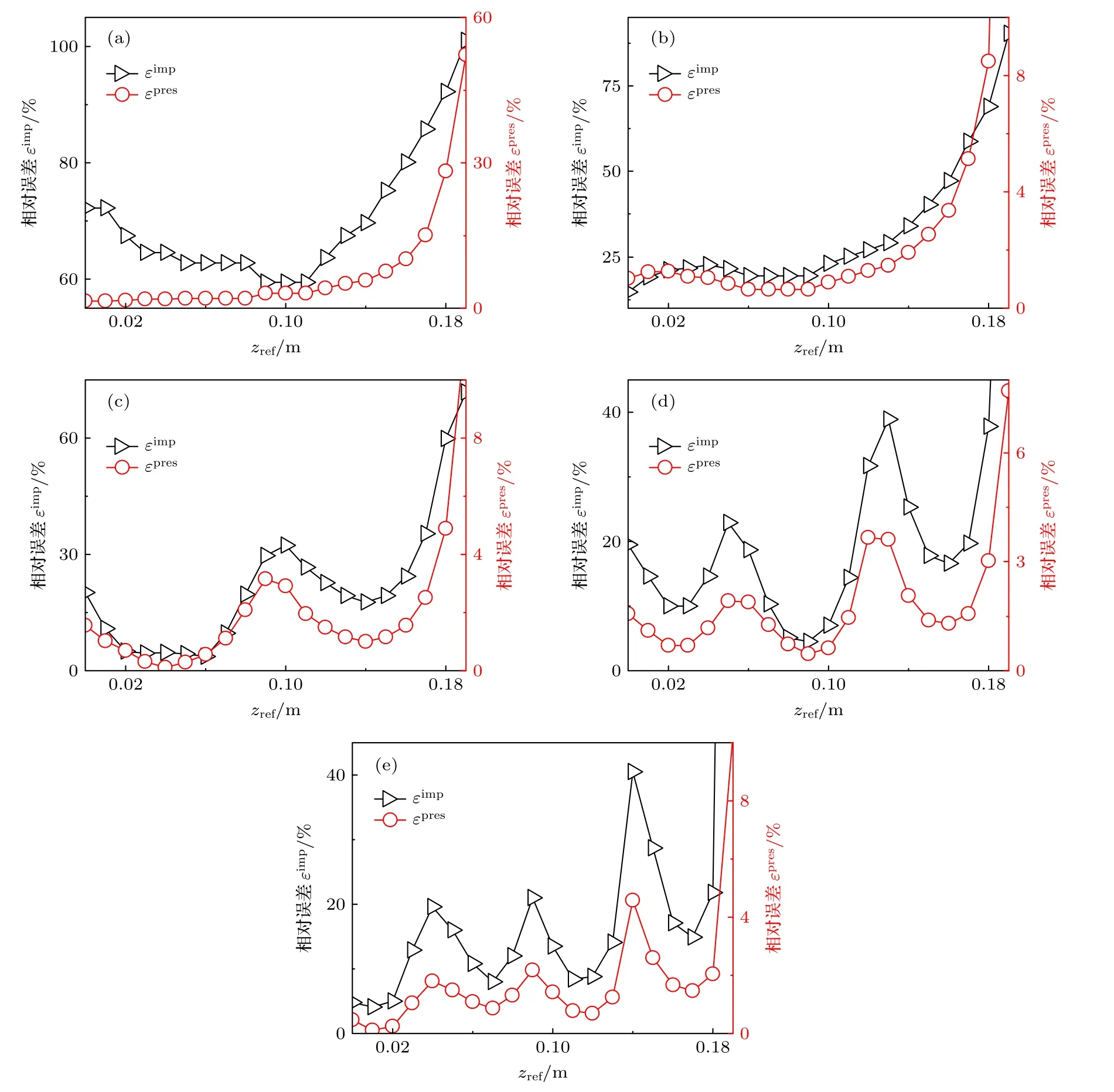
图7 声阻抗率重构的相对误差 εimp和声源直接辐射声压重构的相对误差 εpres随参考传声器坐标 zref的变化曲线 (a)f 100 Hz;(b) f900 Hz;(c) f1700 Hz;(d) f2500 Hz;(e)f 3300 HzFig.7.Relative error of the reconstructed specific acoustic impedance εimp and the relative error of the reconstructed sound pressure εpres radiated directly from the source versus coordinate of the reference microphone zref:(a) f100 Hz;(b) f900 Hz;(c) f1700 Hz;(d) f2500 Hz;(e) f3300 Hz.

先观察声压重构的相对误差εpres随参考传声器坐标zref的变化趋势.首先,在图7 所示的5 幅子图中,随着zref增大,εpres曲线均呈现出一定程度的振荡,在zref0.19 m 处取得最大值;随着声波频率f的增大,曲线振荡的次数增多. 例如,当f900 Hz时,曲线仅有1 个波谷;当f3300 Hz时,波谷的个数增加至4 个;而当f100 Hz 时,εpres单调递增,曲线不存在波谷.其次,对比在不同的f条件下,εpres所取得的最小值,发现在低频时,εpres的最小值相对较大,而在高频时较小.例如,当f100 Hz时,εpres的最小值为 1.44% ,当f2500 Hz和3300 Hz 时,εpres的最小值仅为0.47%和 0.12%.再次,观察不同的f条件下,εpres曲线的波谷所对应的zref值,可以发现,在zref约为 1/4 声波波长时,曲线第1 次出现波谷,而相邻两个波谷之间的间隔约为 1/2声波波长.例如,当f2500 Hz时,对应声波波长为 0.137 m,εpres曲线的第1 波谷在zref0.03 m 处,第1 波谷与第2 波谷的间隔为 0.06 m,第2 波谷与第3 波谷的间隔为0.07 m.

上述现象表明,参考传声器坐标的设置会对声压重构精度产生较大影响,并随着声波频率的不同而呈现差异.当频率较低,声波波长较长时,传声器阵列接收到的边界反射波偏离平面波假设较远,此时,基于半空间球面波函数叠加的半空间数学模型对总声压场的描述精度较低,使得εpres曲线的最小值大于高频工况下的最小值;同时,由于波长较长,参考传声器在较小范围内的移动对其所测得的半空间总声压并无太大影响,导致εpres随zref的增大,呈缓慢地单调递增趋势.因此,在低频工况下,宜将参考传声器设置在紧靠阻抗边界处.

随着频率逐渐增大,声波波长变短,半空间数学模型对总声压场的描述精度提高,使得εpres曲线的最小值降低;同时,当参考传声器坐标zref改变时,测得的总声压随着zref的变化而发生周期性变化,使得εpres曲线出现振荡.此时,宜将参考传声器设置在距离阻抗边界约 1/4 声波波长处.

边界声阻抗率重构的相对误差εimp曲线与εpres曲线的变化趋势具有相似性,仅在频率f100 Hz的工况略有差异.两条曲线具有相似性,是因为声阻抗率和声源直接辐射声压的重构均基于反射系数的估算,其重构精度同时取决于所求得的反射系数均值是否能逼近于其最优值.而差异性则表明,声阻抗率的重构精度对所求得的反射系数均值更为敏感.这是因为声压的重构是以阵列测得的一组总声压值作为输入,反射系数均值近似实际反射系数所引入的误差,会在求解基函数系数时得到补偿.相比而言,声阻抗率是根据反射系数均值直接计算得到,反射系数均值与其最优值的偏离程度直接对声阻抗率的重构结果产生影响.

4.2 边界参数

考察不同边界阻抗条件下,本方法对声阻抗率和声源直接辐射声压的重构精度.为了更符合物理实际,仍然假定边界声阻抗率符合声阻抗模型(15)式,通过考察有效流阻率σe和孔隙度随深度的降低率αe两个边界参数,来间接考察边界阻抗的变化所产生的影响.

首先,考察参数σe的变化对重构精度的影响,考察范围为σe10—1000 kPa·s/m2.设定声波频率f1700 Hz,孔隙度随深度的降低率αe15 m−1,网格步长∆x∆y0.001.由4.1 节可知,参考传声器的坐标会极大地影响重构精度,见图7(c).在此,考察参考传声器坐标在较优配置和较差配置条件下,参数σe的变化对重构精度的影响.在图7(c)所示误差曲线的“波峰”和“波谷”附近选取4 个点,其横坐标依次为0,0.05,0.10 和0.15 m.在这4 个参考传声器坐标条件下,使用本方法重构边界声阻抗率和声源直接辐射声压,所得相对误差εimp和εpres随参数σe的变化曲线分别如图8(a)—(d)所示.

先观察声压重构的相对误差εpres随有效流阻率σe的变化.在图8(a)和图8(c)中,随着σe的增大,εpres呈单调递增趋势.在图8(b)和图8(d)中,εpres随着σe的增大而单调递减.

图8 声阻抗率重构的相对误差 εimp和声源直接辐射声压重构的相对误差 εpres随边界参数 σe的变化曲线 (a) zref 0;(b)zref 0.05 m;(c) zref 0.10 m;(d)zref 0.15 mFig.8.Relative error of the reconstructed specific acoustic impedance εimp and the relative error of the reconstructed sound pressure εpres radiated directly from the source versus boundary parameter σe:(a) zref 0;(b) zref 0.05 m;(c) zref 0.10 m;(d) zref 0.15 m.

注意到,参数σe的增大,导致边界声阻抗率增大,一方面会使得边界反射声在半空间总声压场中所占比重增大.由于基于半空间球面波函数叠加的半空间数学模型对总声压场的描述是近似解,对边界反射声的描述精度较低,所以,随着边界反射声所占比重的增大,半空间数学模型对总声压场的描述精度将会降低.另一方面,随着边界声阻抗率增大,阻抗边界逐渐向完全刚性边界转变,半空间任意场点的反射系数均逐渐趋近于1,数学模型由近似解转变为精确解,导致对总声压场的描述精度提高.这两种效应对声压重构精度的影响完全相反,哪一种效应占主导作用则取决于参考传声器坐标的设置.

在图8(a)和图8(c)中,参考传声器坐标对应图7(c)所示曲线的波峰,所求出的反射系数均值偏离其最优值,以该反射系数均值近似实际反射系数之后,所得半空间数学模型对边界反射声的描述精度较低.随着反射声在总声压场中所占比重的增大,声压重构精度逐渐降低,εpres逐渐增大.在图8(b)和图8(d)中,参考传声器坐标对应曲线的波谷,所求出的反射系数均值接近其最优值,半空间数学模型对总声压场描述精度相对较高.同时,随着σe的增大,半空间数学模型趋近于精确解,使得声压重构精度提高,εpres逐渐减小.

在图8 所示的4 幅子图中,声阻抗率重构的相对误差εimp随有效流阻率σe的增大均呈递增趋势.这表明,边界反射声在半空间总声压场中所占比重是影响声阻抗率重构精度的主要因素.由于声压反射系数均值的求取是以参考测点处总声压重构的相对误差为最小作为准则,当边界反射声所占比重逐渐增大时,为了使得总声压的重构误差最小,算法会自动调整反射系数均值,使其偏离于全息测量面几何中心处的实际反射系数,因此,εimp随着σe的增大而逐渐增大.

接着,考察孔隙度随深度的降低率αe这一边界参数的变化对重构精度的影响,考察范围为αe=10—250 m–1.设定声波频率f1700 Hz,有效流阻率σe=38 kPa·s/m2,网格步长∆x∆y0.001.当zref分别为0,0.05,0.10 和0.15 m 时,使用所提方法重构边界声阻抗率和声源直接辐射声压,所得相对误差εimp和εpres随参数αe的变化曲线分别如图9(a)—(d)所示.

先观察εpres的变化趋势.在图9(a)和图9(c)中,随着αe的增大,εpres单调递增;而在图9(b)和图9(d)中,εpres呈下降趋势.这一变化趋势与图8所示类似,因为与参数σe一样,参数αe的增大同样能使得边界声阻抗率增大,而产生了两种影响声源直接辐射声压重构结果的效应.这两种效应对声压重构精度的影响机理已如前所述.

观察εimp的变化趋势发现,在图9(a)和图9(c)中,εimp随αe的增大而逐渐增大,仅在αe=250 m–1时,图9(c)中的εimp略有减小,这与图8(a)和图8(c)中的变化趋势相似.而在图9(b)和图9(d)中,εimp随着αe的增大,呈现先减小后增大、或先增大后减小的趋势,这与图8(b)和图8(d)所示的单调变化趋势有所不同.这是因为,由声阻抗模型(15)式可知,参数αe的增大所引起的边界阻抗的变化幅度远远不及参数σe.尽管边界反射声所占比重在一定范围内的增大会导致εimp增大,然而,由于参考传声器处于波谷,边界阻抗的增大使得半空间数学模型的描述精度提高,所求得的反射系数均值能够在一定程度上逼近于最优值,这两种因素的共同作用使得图9(b)和图9(d)中的εimp曲线呈现出非单调变化的趋势.

图9 声阻抗率重构的相对误差 εimp和声源直接辐射声压重构的相对误差 εpres随边界参数 αe的变化曲线 (a) zref 0;(b) zref 0.05 m;(c) zref 0.10 m;(d)zref 0.15 mFig.9.Relative error of the reconstructed specific acoustic impedance εimp and the relative error of the reconstructed sound pressure εpres radiated directly from the source versus boundary parameter αe:(a) zref 0;(b) zref 0.05 m;(c) zref 0.10 m;(d) zref 0.15 m.

5 结论

基于半空间球面波基函数叠加的声源直接辐射重构方法,将半空间总声压表述为有限项半空间球面波基函数的叠加,建立半空间各场点总声压之间、以及场点总声压与声源直接辐射声压之间的数学关系,通过在声源近场布置声压全息测量面并设置一支参考传声器,估算各全息测点的声压反射系数,进而重构声源直接辐射的声压场.从而,该方法的提出摆脱了常规方法对于声阻抗原位测量技术的依赖,极大地提高了工程实施的效率.本文对这一方法进行详细的参数讨论,并在估算声压反射系数的基础上,进一步对边界声阻抗加以重构,提出一种基于近场声全息的声阻抗测量方法.

选取脉动球为声源对象,选取以有效流阻率和孔隙度随深度的降低率作为参数的声阻抗模型来模拟实际的物理边界,对边界声阻抗和声源直接辐射声压的重构进行了仿真,定量地分析参考传声器坐标、边界有效流阻率和边界孔隙度随深度的降低率等参数对重构精度的影响.结果表明,本文提出的方法在所考察的频率范围内,能够精确地重构出脉动球声源的直接辐射声压场,并能以一定的精度重构出边界的声阻抗;合理地设置参考传声器坐标对于提高边界声阻抗和声压重构精度至关重要,一般应将参考传声器设置在距离阻抗边界约 1/4 声波波长处,以获取高精度的重构结果;当参考传声器坐标设置不合理时,有效流阻率和孔隙度随深度的降低率两个边界参数的增大,均会导致声阻抗和声压重构精度的降低;而当参考传声器坐标合理设置时,两个边界参数的增大均会促进声压重构精度的提高.

本文的研究内容为半空间中声源直接辐射声场重构方法在实施过程中的参数设置提供了参考,也为边界声阻抗的原位测量开辟了新途径.