石墨烯p-n 结在磁场中的电输运热耗散*

方静云 孙庆丰2)†

1) (北京大学物理学院,量子材料科学中心,北京 100871)

2) (北京量子信息科学研究院,北京 100193)

石墨烯是一种特殊的二维材料,其独特的能带结构允许人们通过电场来调控其载流子的类型和浓度,因此,在构建双极型纳米电子器件方面具有潜在应用前景.本文基于紧束缚格点模型,利用非平衡格林函数方法及Landauer-Büttiker 公式,研究了石墨烯p-n 结在磁场中的电输运热耗散问题.在强磁场作用下,结的两边均处于量子霍尔相,存在拓扑保护的手性边缘态.直觉上,这种拓扑保护的手性边缘态应当是无热耗散的.但本文研究发现,当有耗散源时,尽管手性边缘态受到拓扑保护,热耗散却依然可以发生.对于完美的石墨烯,单极结输运时热耗散发生在体系边缘;偶极结输运时在体系边缘和结的界面处均可以发生热耗散.当无序存在时,无论单极结还是偶极结,无序均能增强热耗散.此外,本文还研究了不同位置处的电子能量分布,发现热耗散是否发生只取决于电子是否处于非平衡分布.这些结果表明拓扑只能保护电子的传播方向,却不能禁止热耗散的发生.

1 引言

量子霍尔效应的发现是20 世纪凝聚态物理学领域中的一项重大成就.1980 年,von Klitzing 等[1]在研究金属-氧化物-半导体场效应晶体管中的二维电子气的输运性质时发现,在低温和强磁场下,霍尔电阻偏离了与磁场的线性关系,呈现出一系列量子化的电阻平台,并且与之对应的纵向电阻是零.这一现象就是著名的量子霍尔效应.自从量子霍尔效应发现以来,一直吸引着人们的广泛关注[2−7].当存在强磁场时,电子在洛伦兹力的作用下做局域回旋运动,能谱演变成一系列分立的朗道能级[5,8].当费米能级位于朗道能级之间时,二维体系内部绝缘而边缘导电,因此对霍尔电阻有贡献的是处于边缘的ν个导电通道(边缘态),从而会导致量子化的霍尔电阻.量子霍尔效应的手性边缘态是受到拓扑保护的,也就是说电子在磁场下只能沿着样品的边缘向一个方向(顺时针或逆时针)传播,因此背散射不会发生,使得量子霍尔效应的纵向电阻为零[9−11].一般情况下,电子输运过程中产生的热耗散与电阻成正比(QI2R),因此人们预期当体系处于量子霍尔相时,其热耗散也应为零.

最近,Halbertal 等[12]利用放置在极细探针上的超导量子干涉仪(SQUID-on-tip,SOT),实现了一种具有微开尔文灵敏度的超灵敏纳米扫描温度计,这为研究纳米尺度的热耗散提供了一种非常有效的技术.采用这种SOT 技术,他们探测了石墨烯中由单个原子缺陷引起的电输运热耗散[13].石墨烯是一种由碳原子紧密排列成单层六角蜂窝状晶格结构的新型二维材料,它具有独特的能带结构,在狄拉克点附近具有线性色散关系.在强磁场下,石墨烯可以展现出独特的量子霍尔效应[14−21].2019 年,Marguerite 等[22]利用SOT 技术研究了石墨烯处于量子霍尔相时的电输运热耗散,发现热耗散沿着手性边缘态的下游流动方向发生(即热耗散从源电极与中间石墨烯耦合的窄口处开始发生,然后发生在沿着手性边缘态流动方向的后端路径上).该实验表明了受拓扑保护的量子霍尔效应中也会发生热耗散.这一反常结果引起了人们的广泛关注,陆续有研究工作围绕此展开[23−26].例如,Zhang 等[23]研究了当石墨烯处于量子霍尔相时,由共振杂质带来的热耗散;Fang 等[24]从理论上阐明了处于量子霍尔相的石墨烯的确可以发生热耗散,且该过程伴随着电子能量分布从非平衡到平衡的演变.

实验上,通过局域地改变栅电压,可以调节石墨烯中载流子的类型和浓度,从而构造石墨烯p-n结[27−29].前人在石墨烯p-n 结的研究中已经发现了很多有趣的物理现象[30−34],如分数化的量子电导[29,30]、Klein 隧穿[31,32]、Veselago 棱镜[33]等.在石墨烯p-n 结中引入强磁场,结的两边将处于量子霍尔相,其中的载流子在拓扑保护下也沿着手性边缘态传播[35−37].既然在处于量子霍尔相的石墨烯中,沿着手性边缘态的下游流动方向可以发生热耗散,那么在强磁场下的石墨烯p-n 结中,沿着手性边缘态是否也会发生热耗散呢? 为了回答该问题,本文基于紧束缚格点模型,利用非平衡格林函数方法及Landauer-Büttiker 公式研究了磁场下完美和无序石墨烯p-n 结中电流诱导的局域热产生和电子能量分布[38−40],即电输运的热耗散问题.在耗散过程中,能量将从有序化电能转化为热能并转移到环境中.为了模拟该过程,本文采用Büttiker 虚拟导线来模拟体系中的耗散源,通过电子在体系和虚拟导线之间的传输,可实现能量交换并发生耗散[24,40].研究表明,在强磁场下的石墨烯p-n 结中,沿着手性边缘态可以发生热耗散,且发生热耗散的具体位置与结两边的填充因子有关.对于完美的单极石墨烯结,如果左右填充因子相等,体系中没有热耗散;如果左右填充因子不等,热耗散主要发生在体系的边缘.对于完美的偶极石墨烯结,如果填充因子较小,热耗散主要发生在结的界面上;如果填充因子较大,热耗散在结的界面和体系边缘均可以发生.当存在无序时,无论单极结还是偶极结,无序均会明显增强热耗散.此外,本文还研究了局域电子能量分布.发现只要某一位置上的电子处于非平衡分布,在该位置就可以发生热耗散,而处于平衡分布时则没有热耗散.这为人们设计低耗散电子器件提供了理论基础.

2 理论模型和方法

考虑一个如图1(a)所示的两端石墨烯p-n 结体系.采用紧束缚格点模型来描述该体系,它的哈密顿量如下[41−44]:

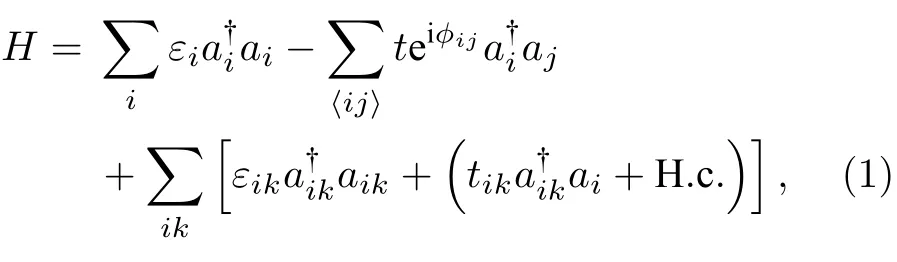
其中前两项是石墨烯p-n 结在磁场下的哈密顿量.i(x,y)表示格点的离散位置坐标,如图1(a)所示.和分别表示格点i上粒子的产生和湮灭算符,εi是格点i处的在位能,即狄拉克点的能量,实验上可以通过调节栅电压来控制在位能[27−29].整个装置可以分成左导线、中心区 CI−III和右导线三个部分.在左(右)导线和中心区 CI(中心区 CIII),在位能εi等于EL(ER);而在中心区 CII,考虑到电势的变化和Anderson 无序的存在,在位能εik(ER−EL)/(2M+2)+EL+ωi,其 中k1,2,...,2M+1(图1(a)).ωi是无序势能,它在[−W/2,W/2]范围内随机取值,W是无序强度.第二项中的t代表最近邻格点之间的跃迁能.考虑该石墨烯p-n 结体系处于一个垂直外磁场下,这会在近邻格点跃迁能上引起一个磁通相位ϕij.选取洛伦兹规范,外磁场B的磁矢势A(−By,0,0) ,引起的磁通相位ϕij是磁通量子.因为在真实体系中,不可避免地存在各种耗散源,如电子-声子相互作用等.因此在本文中,采用Büttiker 虚拟导线来模拟耗散源.为了研究电流沿着边缘态的热耗散情况,除了中心区 CII的格点外,我们给靠近中心区CII的 CI区和 CIII区的一部分格点也加上耗散源,即图1(a)中的每个红色格点都耦合一根Büttiker 虚拟导线.(1)式中第三项描述这些Büttiker 虚拟导线以及它们与相应格点之间的耦合哈密顿量,和aik分别表示格点i处的虚拟导线中粒子的产生和湮灭算符,tik代表虚拟导线和中心区格点之间的耦合强度.

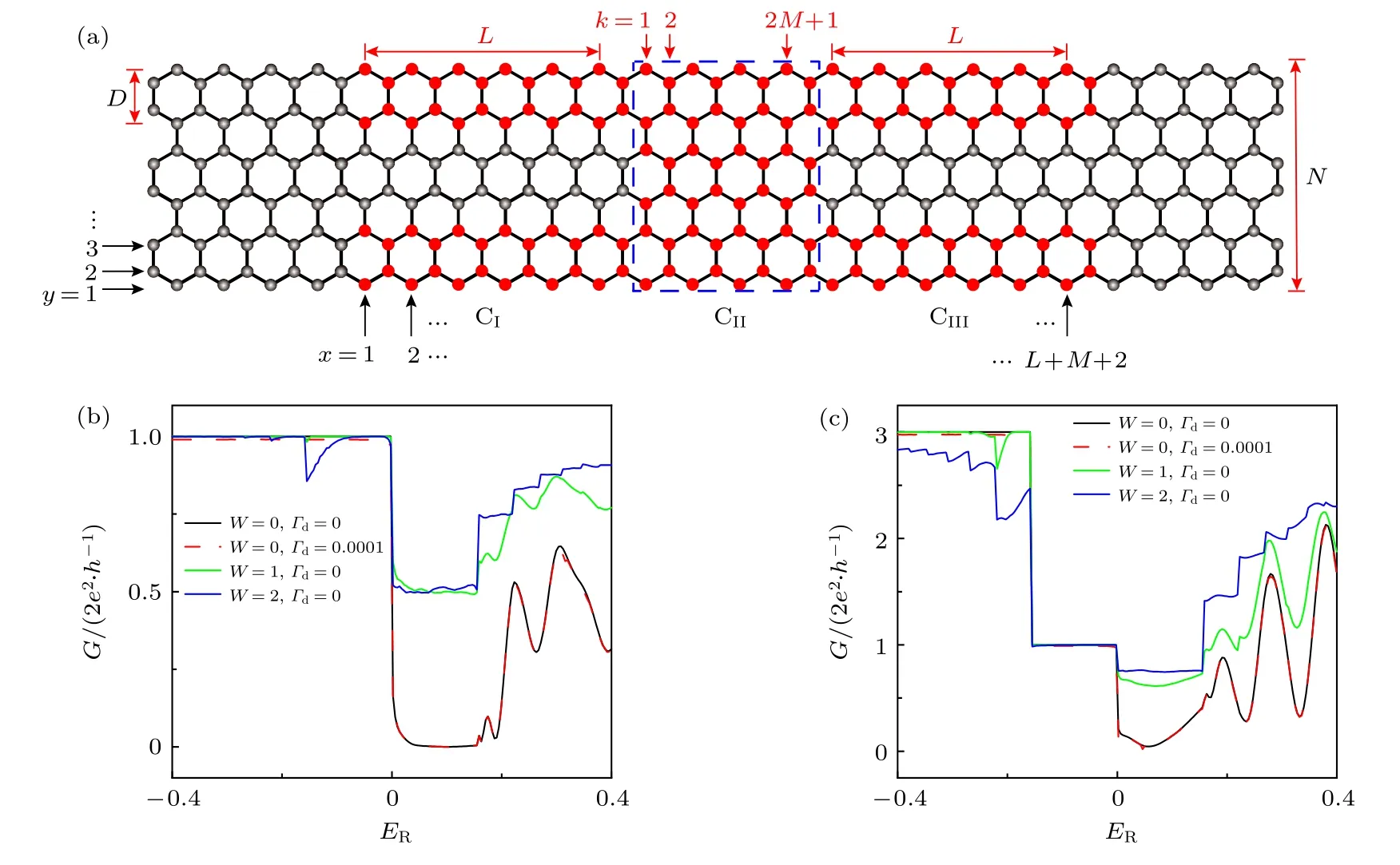
图1 (a) 锯齿型石墨烯p-n 结示意图,红色格点表示在这些格点上耦合了虚拟导线,图中 D4,N 12,L11,M 3;(b),(c) 不同无序强度W 下电导G 随着 ER的变化曲线.当 W0时,无序构型平均取 2000次.图(b)中 EL −0.1 (νL 1),图(c)中 EL −0.2 (νL 3)Fig.1.(a) Schematic diagram for a zigzag graphene p-n junction.The red sites indicate that virtual leads are coupled to these sites,and D4,N 12,L11,M 3 in this diagram.(b),(c) The conductance G vs. ER for different disorder strengths W.Here the conductance is averaged up to 2000 configurations when W0. The parameters EL −0.1 (νL 1) in panel (b),EL −0.2(νL 3) in panel (c).

由零温下的多端口Landauer-Büttiker 公式,从端口p流入体系的电流和热流为[24]

在下面的数值计算中,以跃迁能t ≈2.75 eV作为能量单位,费米能EF0.外磁场B用ϕ表示,其中是一个六角蜂窝状晶格中的磁通,a ≈0.142 nm 是两个最近邻碳原子之间的距离.计算时,取ϕ0.007,对应磁长度体系宽度N200,对应体系的真实宽度为 (3N−1)a21.2 nm.由此可见,磁长度lB远小于体系的宽度,因此上下边缘态在传播过程中不会直接发生混合.体系的其他尺寸参数为L79,M10,D20.此外,为了保证加入耗散源后不影响体系的输运,取耗散源强度Γd0.0001.

3 结果与讨论

首先研究该石墨烯p-n 结体系的电导.图1(b)和图1(c)给出了电导G随着右导线狄拉克点能量ER的变化.从图1(b)和图1(c)可以看出,Γd0.0001(红色曲线)时电导G随ER变化的曲线和Γd0(黑色曲线)时几乎重合,说明弱耗散源的存在并不影响体系的输运.为简化计算,之后取Γd0计算电导.先考虑完美的石墨烯(无序强度W0)的情况,ER<0时(n-n 结,即左右填充因子νL,νR大于0),电导G展现出一系列量子化的平台,平台值由min(|νL|,|νR|)2e2/h决定[29,35].ER>0 时(n-p 结,即νL>0,νR<0),电导G非常小.因为在完美的石墨烯n-p 结中,左右两个区域上电子和空穴的边缘态具有不同的手性且彼此在空间上分离,因此边缘态的混合几乎没有发生,从而导致电导非常小.当体系中存在无序时(W0),在n-n 结中,如果无序强度较小,电导G的量子化平台依旧保持且数值几乎不变(图1(b));如果无序强度较大,手性边缘态会被强无序破坏,电导G的量子化平台消失且数值减小(图1(c)).在n-p 结中,引入无序后电子型和空穴型的边缘态在结的界面附近发生混合,使得电导G明显增大.此外,在合适的无序强度下,电子型和空穴型的边缘态在结的界面附近完全混合,会导致一些分数化的量子电导平台出现[46],平台值为 [|νL||νR|/(|νL|+|νR|)]2e2/h.例如,当(νL,νR)(1,−1)时,出现了 (1/2)2e2/h的电导平台;当(νL,νR)(3,−1)时,出现了 (3/4)2e2/h的电导平台.上述结果均与已有文献的计算结果一致[43,47].下面研究耗散源存在时,完美的石墨烯单极结和双极结体系中的热耗散情况.先考虑单极结输运,即结的两边参与输运的载流子同为电子(n-n结)或同为空穴(p-p 结).图2(a)和图2(b)给出了石墨烯n-n 结中的局域热产生QL随着格点位置坐标 (x,y) 的变化,对于p-p 结,其结果和n-n 结类似.在图2(a)中,左右填充因子 (νL,νR)(1,1),可以看到此时体系中没有热耗散.因为当νLνR时,电子在磁场作用下沿着手性边缘态逆时针传播;特别地,在传播过程中,电子始终处于平衡分布,因此没有热耗散发生.在图2(b)中,左右填充因子(νL,νR)(3,1),可以看到此时热耗散主要发生在体系的左上边缘.因为当νLR时,尽管电子依旧沿着手性边缘态逆时针传播,但由于νL>νR,从左端νL个模式流出的电子在到达n-n 结界面时,有νR个模式会进入右端,而剩余的νL−νR个模式则会沿着n-n 结的界面传播[36].在到达上边缘时,它们会和从右端流入的νR个模式一起沿着上边缘继续逆时针传播,如图2(b)中带箭头的黑色实线所示.因此,在沿着左上边缘传播的电子中,既有来自于左端电子库的电子,又有来自于右端电子库的电子,所以电子在左上边缘处于非平衡分布,从而导致热耗散在左上边缘发生.此外,在n-n 结的界面上,靠近上边缘的位置也会发生热耗散,这是因为沿着n-n 结界面传播的电子在到达上边缘时有一部分会被反弹回来,使得n-n 结界面上靠近上边缘处的电子也处于非平衡分布,从而导致在n-n 结界面上靠近上边缘的位置发生了热耗散.

接下来考虑偶极结输运,即结的两边参与输运的载流子分别是电子和空穴(n-p 或p-n 结).图2(c)和图2(d)给出了n-p 结中的局域热产生QL随着格点位置坐标 (x,y) 的变化;对于p-n 结,结果是类似的.在图2(c)中,左右填充因子 (νL,νR)(1,−1),可以看到,此时热耗散主要发生在n-p 结的界面上.在图2(d)中,左右填充因子 (νL,νR)(3,−3),可以看到,此时热耗散在n-p 结的界面和上边缘均会发生而且明显增强.这是因为,偶极输运时结两边的载流子沿着相反的方向朝结界面汇聚,在结的界面上形成了多模式的边缘态[35],因此n-p 结界面上的电子处于非平衡分布,从而导致热耗散在n-p结界面上发生.当填充因子比较小时,边缘态数目少且彼此在空间上分离,因此上边界的电子能量分布近似为平衡分布,没有热耗散(图2(c)).而对于较大的填充因子,n-p 结的界面上会有更多的边缘态出现,且它们彼此之间在空间上有一定的混合,使得沿着结界面传播到上边缘的电子也处于非平衡分布,从而导致在上边缘也有热耗散发生(图2(d)).此外,在靠近n-p 结界面的上下边缘上,也会发生热耗散.因为结两边的载流子传播到结的界面时,会有一定的可能性被结界面反弹.因此上下边缘上靠近n-p 结界面处的电子也处于非平衡分布,从而导致在这些位置上发生了热耗散.

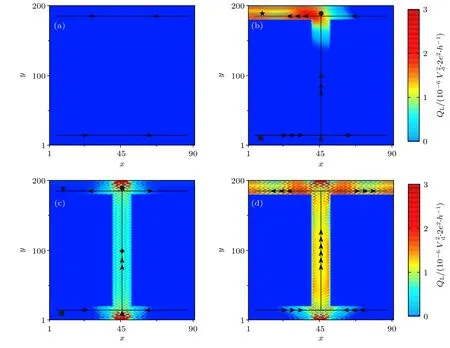
图2 局域热产生 QL随着格点位置坐标 (x,y) 的变化,带箭头的黑色实线代表手性边缘态的数目和传播方向.符号■,▲,◆,●,★标记的位置分别是 (10, 10) ,(46,10) ,(46,100) ,(46,190) ,(10,190),在 图4 中将给出这些位置上的电子能量分布.(EL,ER)=(−0.1,−0.1)(a) ,(−0.2,−0.1)(b),(−0.1,0.1)(c),(−0.2,0.2)(d),分别对应左右填充因子 (νL,νR)(1,1)(a),(3,1)(b),(1,−1)(c),(3,−3) (d)Fig.2.Local heat generation QLvs.lattice position (x,y),the black solid lines with arrows represent the number and propagation direction of the chiral edge states.Positions marked by symbols ■,▲,◆,●,★ are,respectively,(10,10) ,(46,10) ,(46,100),(46,190),(10,190) ,and energy distribution of electrons at these positions will be shown in Fig.4. (EL,ER)(−0.1,−0.1) (a),(−0.2,−0.1)(b),(−0.1,0.1)(c),(−0.2,0.2)(d),which correspond to the left and right filling factors (νL,νR)(1,1)(a),(3,1)(b),(1,−1)(c),and (3,−3) (d),respectively.

上面已经分析了完美的石墨烯体系中的热耗散情况.接下来,研究无序对热耗散的影响.图3(a)和图3(b)给出了无序存在时石墨烯n-n 结中的局域热产生QL随着格点位置坐标 (x,y) 的变化.与完美的石墨烯n-n 结相比(图2(b)),热耗散不仅会发生在体系的左上边缘,还会发生在结的界面上.因为当结界面上存在无序时,电子在结界面上传播会发生散射.因此在结的界面上,电子也处于非平衡分布,从而导致热耗散在结的界面上发生.随着无序强度的增加,电子在结界面上的散射增强,因此结界面上的热耗散也明显增强.图3(c)和图3(d)给出了无序存在时石墨烯n-p 结中的局域热产生QL随着格点位置坐标 (x,y) 的变化.从图3(c)和图3(d)可以看到,无序越强,结界面上热耗散也越强.此外,相比于完美的石墨烯n-p 结(图2(c)),此时热耗散不仅会发生在结的界面上,还会发生在体系的上边缘.这是因为无序导致电子型和空穴型的边缘态在结的界面混合[29,35],从而使得沿着结界面传播的电子在到达上边缘时,有一定的概率进入左端口或右端口.因此上边缘的电子也处于非平衡分布,导致热耗散在上边缘发生.

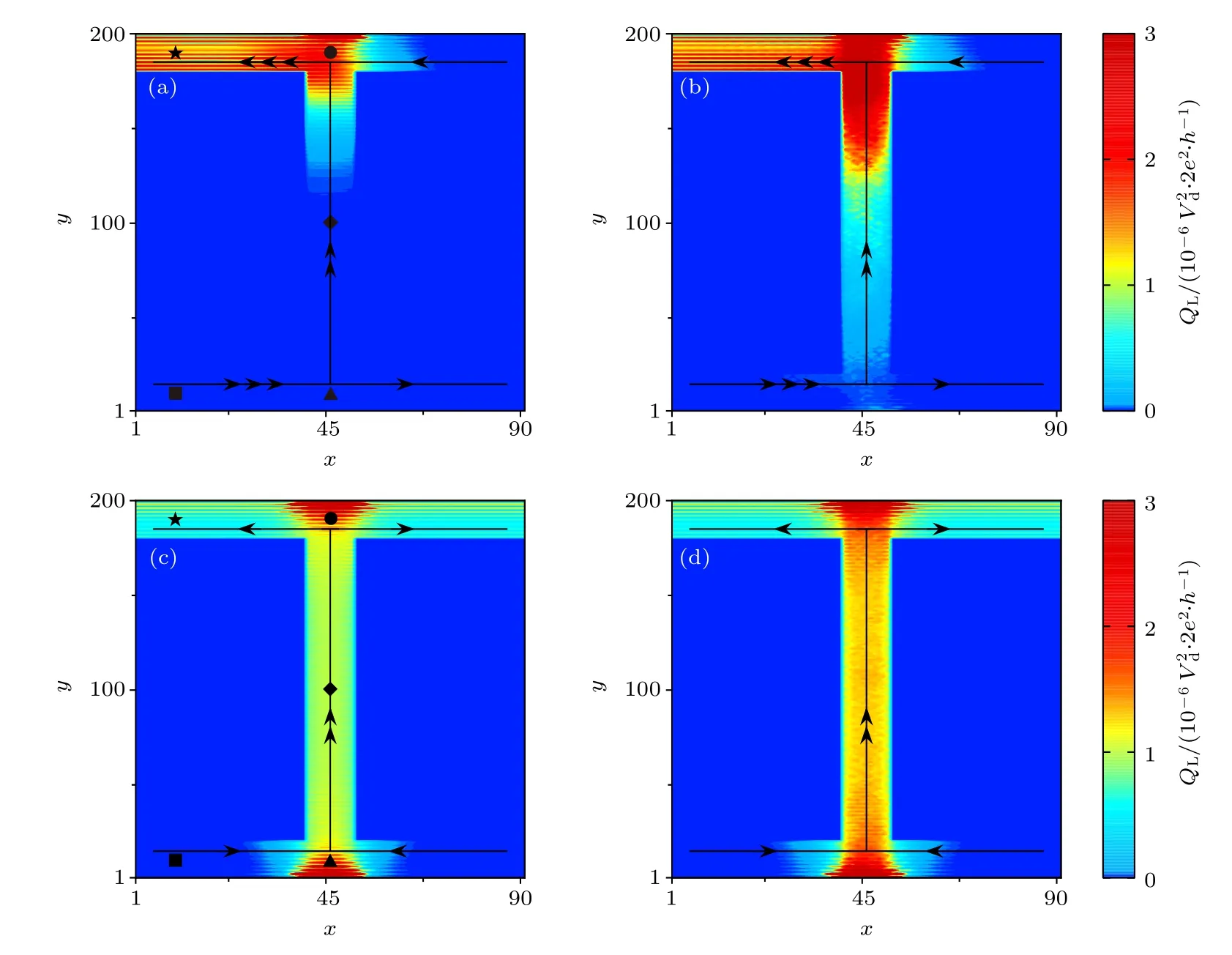
图3 局域热产生 QL随着格点位置坐标 (x,y) 的变化,带箭头的黑色实线代表手性边缘态的数目和传播方向.符号■,▲,◆,●,★标记的位置分别是 (10,10) ,(46,10) ,(46,100) ,(46,190) ,(10,190),在图4 中将给出这些位置上的电子能量分布.(a),(b)(EL,ER)(−0.2,−0.1); (c),(d) (EL,ER) (−0.1,0.1).(a),(c) 无序强度 W1;(b),(d) 无序强度 W 2.无序构型平均取400次Fig.3.Local heat generation QLvs.lattice position (x,y),the black solid lines with arrows represent the number and propagation direction of the chiral edge states.Positions marked by symbols ■,▲,◆,●,★ are (10,10) ,(46,10) ,(46,100) ,(46,190),(10,190),respectively,and energy distribution of electrons at these positions will be shown in Fig.4.(a),(b)(EL,ER)(−0.2,−0.1);(c),(d) (EL,ER)(−0.1,0.1).(a),(c) Disorder strength W1;(b) (d) W 2.Here the local heat generation is averaged up to 400 configurations.

从以上结果可以看出,当电子在某一位置处于非平衡分布时,在该位置上就会发生热耗散,而处于平衡分布时则不会发生热耗散.为了更直观地表明这一结果,下面研究电子在不同位置上的能量分布函数.利用非平衡格林函数方法,某一个格点i上电子的能量分布函数可以表示为

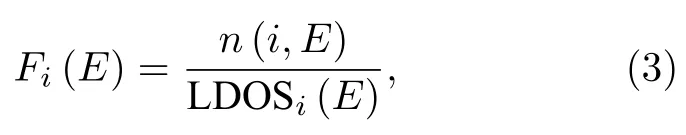
图4(a)和图4(b)分别给出了图2(b)和图3(a)中标记位置处的电子分布函数F随能量E的变化.从图4(a)和图4(b)可以看出,在■,▲,◆三个位置上,电子几乎处于平衡分布;相对应地,在图2(b)和图3(a)中这三个位置上几乎没有热耗散.而在●,★ 两个位置上,电子处于非平衡分布;相对应地,在图2(b)和图3(a)中这两个位置上有热耗散发生.同样地,图4(c)和图4(d)分别给出了图2(c)和图3(c)中标记位置处的电子分布函数F随能量E的变化.图4(c)中,在■和★两个位置上,电子几乎处于平衡分布;对应地,在图2(c)中这两个位置上几乎没有热耗散.而在▲,◆,●三个位置上,电子处于非平衡分布;对应地,在图2(c)中这三个位置上有热耗散发生.图4(d)中,在■标记的位置上,电子几乎处于平衡分布;对应地,在图3(c)中该位置处几乎没有热耗散.而在▲,◆,●,★四个位置上,电子处于非平衡分布;对应地,在图3(c)中这些位置上有热耗散发生.由此可见,只要电子在某一位置上处于非平衡分布,在该位置上就会发生热耗散,而处于平衡分布时则没有热耗散.也就是说,热耗散是否发生只取决于电子是否处于非平衡分布.这说明拓扑只能保护电子的传播方向,却不能禁止热耗散的发生.

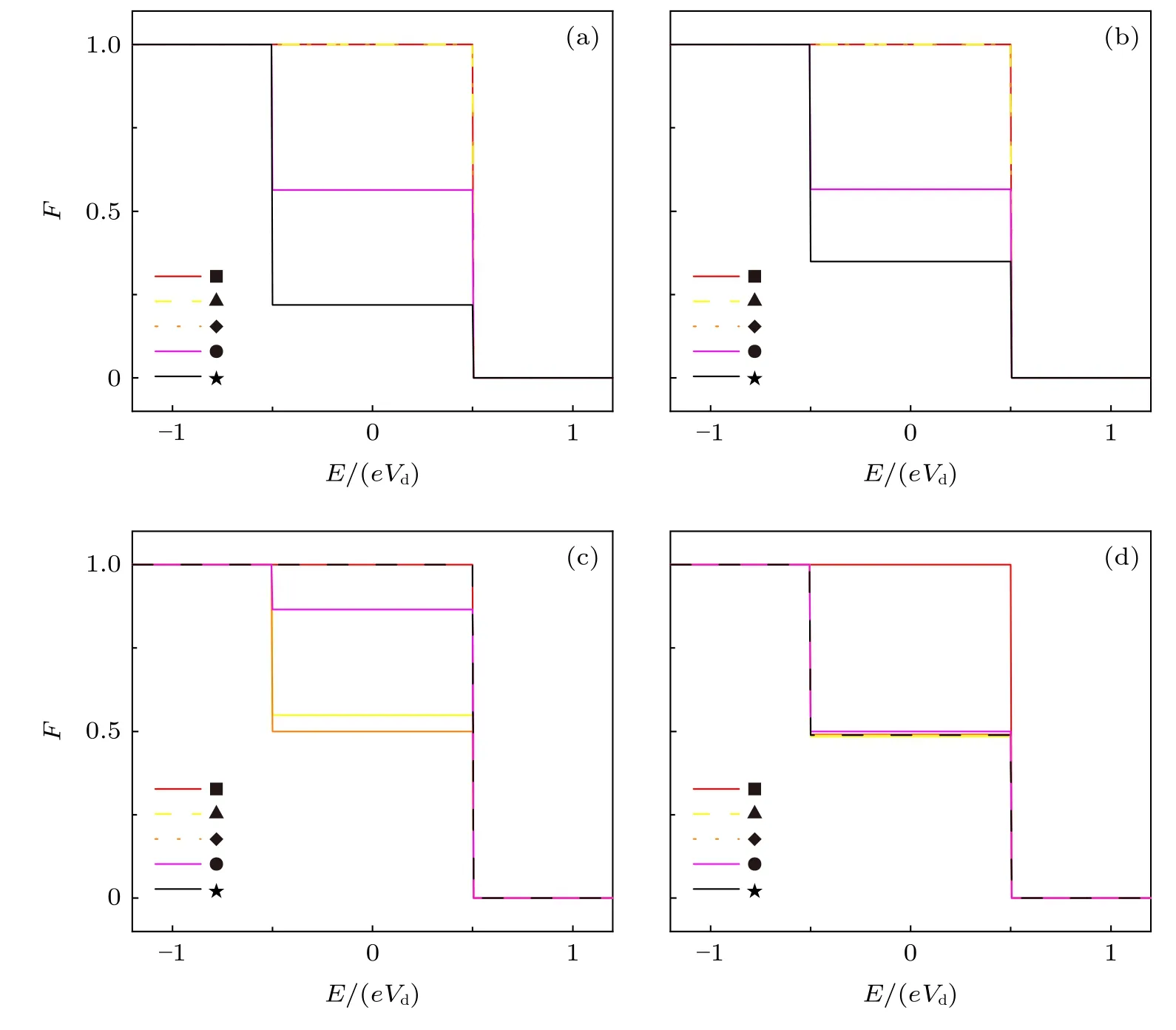
图4 不同位置处的分布函数F 随着能量E的变化,符号■,▲,◆,●,★对应图2 和图3 中标记的位置.(a),(b)(EL,ER)(−0.2,−0.1);(c),(d) (−0.1,0.1).(a),(c) 无序强度 W0;(b),(d) W1.当 W0 时,无序构型平均取 400 次Fig.4.Distribution function F vs.energy E for different positions,the symbols ■,▲,◆,●,★ correspond to positions marked in Fig. 2 and Fig. 3. (a),(b) (EL,ER)(−0.2,−0.1); (c),(d) (EL,ER)(−0.1,0.1). (a),(c) Disorder strength W0;(b),(d) W 1.Here distribution function F is averaged up to 400 configurations when W0.

4 结论

本文研究了石墨烯p-n 结在磁场中的电输运热耗散情况,以及无序对热耗散的影响.研究发现,拓扑只能保护电子的传播方向,却不能禁止热耗散的发生.热耗散是否发生只取决于电子是否处于非平衡分布.在完美的石墨烯中,单极结输运时,如果左右两边填充因子相等,则电子沿着边缘传播时始终处于平衡分布,因此不会发生热耗散;如果左右两边填充因子不等,则某一边缘上会同时存在来自于左右端口的载流子,因此电子在该边缘上处于非平衡分布,从而导致热耗散在该边缘上发生.偶极结输运时,结的界面上会同时存在来自于左右端口的载流子,因此结界面上的电子处于非平衡分布,导致热耗散在结的界面上发生;如果填充因子较大,热耗散还可以在体系的边缘上发生.此外,无序会使得载流子在结界面上发生散射从而增强热耗散.