变工况下钢厂转炉支承螺栓断裂机理分析*

郭 亮,牛 浩,董楚峰,宾光富*

(1.鄂城钢铁炼钢厂,湖北 鄂州 436000;2.湖南科技大学 机械设备健康维护省重点实验室,湖南 湘潭 411201)

0 引 言

在炼钢过程中,支承螺栓承受高温状态下炉体、炉衬及炉液总重约800 t的载荷重量。同时,转炉处于不断绕托圈上耳轴旋转的变工况状态,如吹炼、测温、补吹、出渣、出钢等变角度工况,其支承螺栓承载着传动装置与炉体之间产生的巨大交变应力。

在长期处于转动、启动、制动等变工况条件下,高温重载状态的支承螺栓使用寿命常常小于设计理论寿命,致使支承螺栓根部失效断裂和变形过大等现象经常产生,造成重大的生产、安全事故[1,2]。

支承螺栓断裂可能造成炉体失控下坠、铁水倾覆、托圈漏水、炉液喷爆等安全事故[3,4],不少钢铁企业等都曾发生过类似事例。目前,国内外学者针对转炉支承螺栓装置开展了诸多研究。

郭志强等人[5]采用UG软件对转炉进行了整体建模,并计算出了不同倾角下倾动力矩,用ANSYS软件对转炉进行了整体分析,找出了连接装置处应力变化规律,发现连接装置处存在应力传递不均匀现象;但其对转炉整体进行了有限元建模,计算耗时长,且分析精准度欠缺。梁海琴等人[6]建立了转炉及托圈连接装置的三维整体模型,采用常规接触计算和基于子结构的接触计算方法,得到了托圈及连接装置整体模型和支承螺栓子结构的应力分布;但该研究考虑的工况不全面。YIN Q等人[7]建立了支承螺栓的运动模型,并对其进行了运动学和动力学分析,计算确定了3组螺栓装置上的载荷大小;但该研究未对其做进一步的有限元分析。张培轩[8]采用现场实测与有限元仿真分析相结合的方法,对支承螺栓支承耳板焊缝开裂原因进行了深入分析,结果发现,当支承螺栓倾角变化过大时,其角加速度产生的冲击会诱发焊缝应力集中部位的开裂。

但现有的研究中,忽略了转炉本身复杂的结构及实际运行过程中工况的变化,且其炉体、炉液重量及倾动力矩等物理量多采用简略化的计算获得,未结合转炉实际工况与运行问题,因此,无法精准得到转炉不同工况下螺栓的实际承载情况。

基于此,以某厂130 t转炉为例,笔者建立转炉三维模型,采集转炉实际运行数据,采用MATLAB计算不同角度下转炉的倾动力矩,使用有限元方法对支承螺栓进行力学分析,计算危险截面最大应力应变值,研究支承螺栓断裂机理。

1 转炉支承螺栓受力分析

1.1 转炉基本结构

转炉设备主要包括炉壳、炉衬、炉体和托圈,其三维结构如图1所示。

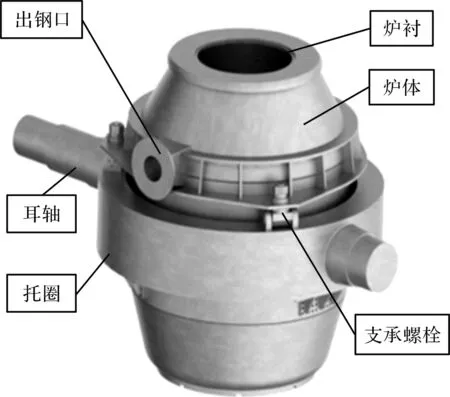
图1 转炉三维结构简图

炉体和托圈联接所用的球面带销轴支承螺栓[9]结构如图2所示。

图2 支承螺栓三维结构简图

转炉支承螺栓互成120°,均匀分布在托圈上,位置为出钢口两侧及对侧。在转炉工作过程中,其所受载荷包括炉体和钢水的静负荷,倾动力矩,启动、制动、碰撞产生的冲击负荷以及环境热应力等。

1.2 支承螺栓倾动力矩计算

当炉体旋转时,作用耳轴上的静力矩被称作转炉的倾动力矩。通过计算倾动力矩值,可以将其作为基本载荷参数,对施加在支承螺栓上的等效应力进行计算[10,11]。

倾动力矩由空炉力矩、炉液力矩和摩擦力矩3部分组成,其计算为:

M=Mk+My+Mm

(1)

式中：Mk—空炉力矩；My—炉液力矩；Mm—摩擦力矩。

空炉力矩Mk是炉壳、炉衬等炉体设备的重量产生的静态阻力矩，其大小与倾动角度α成正弦函数的关系，同时受到空炉重心和自身重量的影响。

不同角度下空炉力矩值计算公式如下：

Mk=Gk·rk·sinα

(2)

式中：Gk—空炉重量；rk—空炉重心到耳轴中心的距离；α—转炉倾动旋转角度值。

空炉力矩及炉液力矩示意图如图3所示。

图3 空炉力矩及炉液力矩示意图

炉液力矩My是由炉内液体包括铁水和炉渣引起的静力矩。在转炉倾动过程中，转炉出钢前，其出钢口闭合，炉液的形状、重心位置随着倾动角度的变化而变化；出钢过程中，炉液重量随倾动角度增大逐渐减小。

考虑极限受力情况，倾动力矩按炉液满载计算，可采用高斯积分法，计算炉液力矩、倾动角度及炉液重量的函数关系，即：

My=Gy[(H-zy)sinα-xycosα]

(3)

式中：Gy—炉液重量；H—转炉耳轴中心Z轴方向坐标值；zy—炉液Z轴方向重心坐标；xy—炉液X轴方向重心坐标。

转炉的摩擦力矩Mm主要在耳轴与倾动装置之间产生，方向始终与转炉倾动方向相反，大小基本不变，在计算中摩擦力矩可近似为常量[12]。

摩擦力矩计算公式如下：

Mm=μ·R·G

(4)

式中：μ—摩擦系数，取0.02；R—耳轴半径；G—转炉装置实际最大重量。

联立式(1～4)，可得倾动力矩表达式：

M=Gk·rk·sinα+Gy[(H-zy)sinα-xycosα]+
μ·R·G

(5)

1.3 支承螺栓受载计算

转炉通过3组支承螺栓装置与托圈相连接,其受力情况[13]示意图如图4所示。

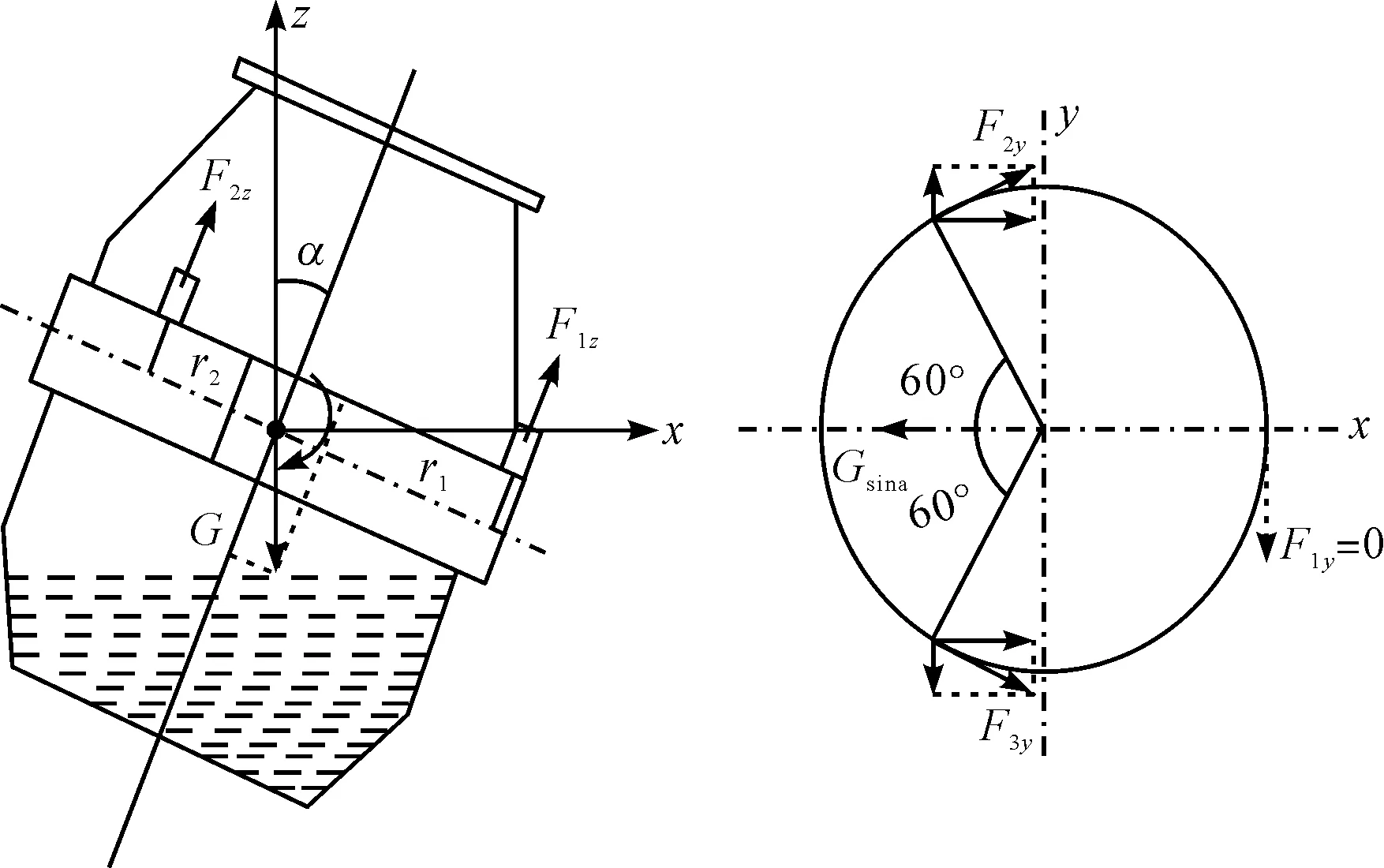
图4 转炉受力示意图

根据其位置，将出钢口对侧螺栓命名为A，出钢口两侧螺栓命名为B。由受力分析可知，转炉在球面副支反力Fiy与Fiz(i=1,2,3)、总重力G以及倾动力矩M共同作用下平衡；其中，作用在转炉本体上的重力G，可分解为平行于托圈的分力Gsinα，以及沿炉体中轴线上的分力Gcosα。

根据力与力矩的平衡方程以及支承螺栓本身的对称条件[14]，可列以下公式：

(6)

根据几何条件可得：

(7)

(8)

式中：α—转炉转动角度；r1—支反力F1z对转炉耳轴中心的力臂；r2—支反力F2z、F3z对转炉耳轴中心的力臂。

由此可见，支承螺栓受载大小主要与倾动角度α有关。

2 支承螺栓建模及应力分析

2.1 支承螺栓有限元建模

以某钢厂130 t转炉为例,根据支承螺栓结构特点,笔者选择螺栓本体及销轴作为主要分析对象;同时,为减少计算时间、增加仿真计算的准确性,对支承螺栓有限元模型进行适当的简化,除去球面垫等具有装配形式模型,通过仿真计算其在各个角度下的应力应变情况[15-19]。

该厂选用的支承螺栓材料为35CrMo,其密度为7.85×103kg/m3,弹性模量为2.06×105MPa,泊松比为0.3。销轴与螺栓之间设置为摩擦接触,摩擦系数为0.15。

支承螺栓受力面划分示意图如图5所示。

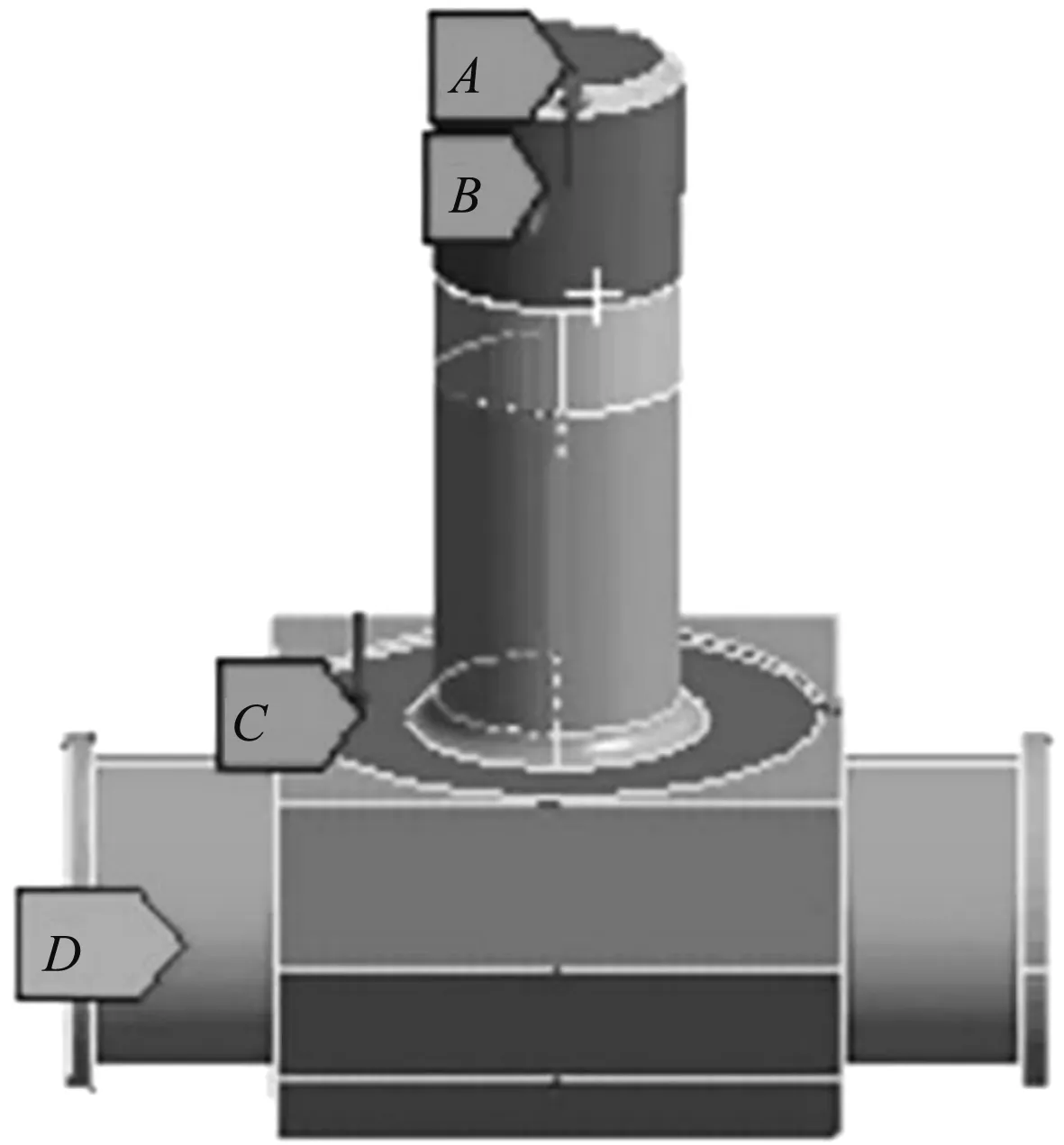
图5 支承螺栓受力面划分示意图

从图5中可知:D为圆柱形约束面,作用在销轴两端;球面垫圈支座平面A、波纹垫圈螺纹副作用面B及支柱螺栓轴向端面C为受力面。

考虑到销轴与销轴座直接受到托圈温度的影响,按照工程经验,笔者将销轴接触温度设置为170 ℃,环境温度为45 ℃,使用四面体网格划分法及单元尺寸调整法划分网格,得到支承螺栓有限元模型;

划分完毕后,共有83 068个节点以及54 542个单元;然后设置有限元求解项,求解支承螺栓最大等效应力及最大等效应变。

2.2 支承螺栓施加载荷计算

该钢厂转炉满载时,炉液重量Gy为160 t,空炉重量Gk为442.6 t,总重G为800 t。

采用该钢厂转炉工程数据,笔者使用MATLAB软件对式(2～5)进行编程计算,得到转炉力矩曲线,如图6所示。

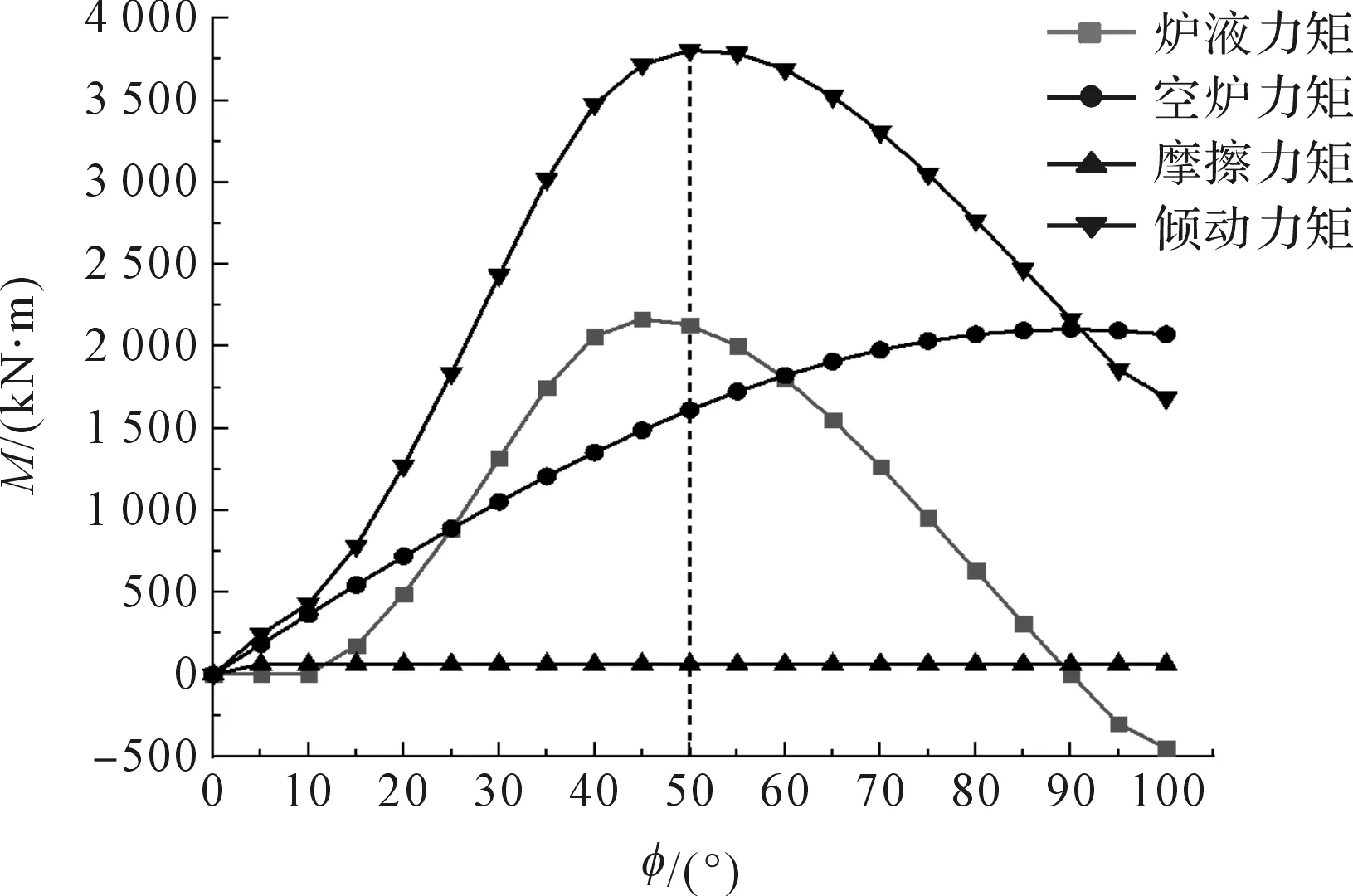
图6 转炉力矩曲线

由图6可看出:其摩擦力矩几乎不变,空炉力矩在90°前呈上升趋势,随后接近平稳;炉液力矩在45°时出现最大值,在90°后出现负值。

综上所述,倾动力矩在50°时出现最大值。

该厂转炉典型工况如表1所示。

表1 转炉典型工况

由表1可知,测温取样、出渣及出钢过程中出现最大倾动力矩,因此,需要对特殊工况下支承螺栓进行受力分析。

将不同角度下转炉总重力及倾动力矩值代入式(8),可得到各个工况下支撑螺栓受载曲线,如图7所示。

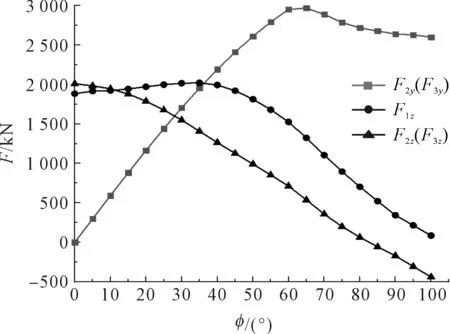
图7 变工况支撑螺栓受载曲线

图7结果表明：支反力F2y与F3y呈先增大后减小的趋势，在65°时出现最大值；支反力F1z先平稳上升后逐渐减小；支反力F2z与F3z则保持逐渐减小的趋势。

根据支承螺栓在不同工况下的受载情况，施加到模型相应的作用表面，由于出钢口对侧与出钢口两侧的支承螺栓受载情况不同，需分别对其进行受力分析。

图5有限元分析模型中3个受力面面积分别为：支承螺栓轴向端面Q1=0.045 24 m2、波纹垫圈螺纹副作用面Q2=0.101 159 m2、球面垫支座平面Q3=0.191 95 m2。

3个受力面载荷计算公式为：

(9)

式中：P1，P2，P3—受力面Q1，Q2，Q3所承受载荷；FP—四波纹垫圈施加额外的预紧力。

四波纹垫圈预紧力[20]作用在球面垫座平面上，其目的是保证支承螺栓装置中的上、下两组球面垫圈正常工作。可通过以下公式计算出预紧力：

(10)

式中：E—材料弹性模量，E=2.1×106kg/cm2；b—垫圈宽度，cm；h—垫圈厚度，cm；δ—波纹垫圈压缩量。

其中，垫圈外径与垫圈宽度的比值N和垫圈平均直径Dm，可通过如下公式计算：

N=D/b

(11)

Dm=(D+d)/2

(12)

式中：D—垫圈外径；d—垫圈内径。

该厂支承螺栓螺母拧紧时，四波纹垫圈的压缩量标准为1.5 mm，叠合总高度为82 mm，由此可得四波纹垫圈预紧力FP=1 031.34 kN；将其代入各项数据，可得螺栓A各个受力面受载的大小，如图8所示。

图8 螺栓A各受力面载荷

螺栓B各个受力面受载的大小如图9所示。

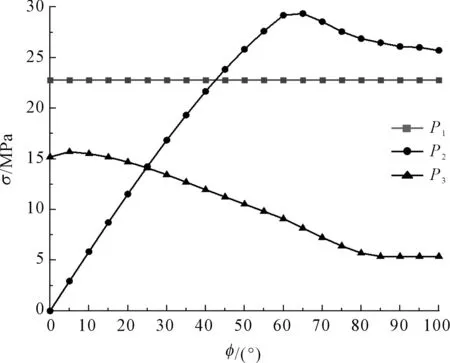
图9 螺栓B各受力面载荷

根据图(8,9)中的各载荷,笔者对不同工况下的支承螺栓进行有限元分析,提取不同工况下其最大等效应力,得出支承螺栓的最大等效应力曲线,如图10所示。

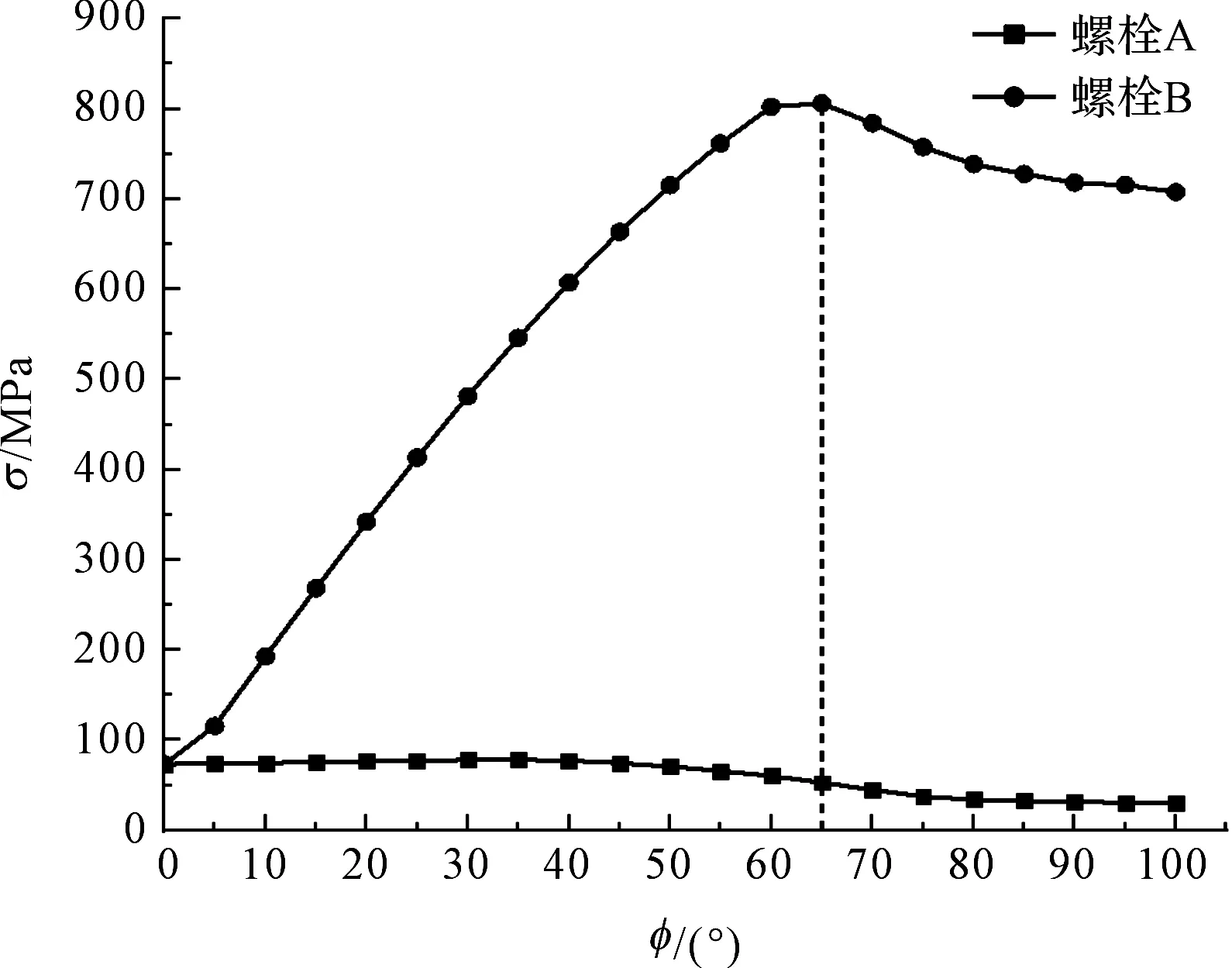
图10 支承螺栓最大等效应力曲线

由图10可知:螺栓B最大等效应力先增大后减小,在65°工况下达到最大;螺栓A最大等效应力逐渐减小,在100°工况下降至最小。

参照转炉典型工况可知,在倾动至测温取样、出渣及出钢过程中,出钢口两侧支承螺栓受力最大。

2.3 倾斜角度65°下支承螺栓应力

上述有限元分析结果显示,不同工况下螺栓应力变化规律相似,但65°工况下最大等效应力高于其他工况,因此,笔者以该工况为例,对出钢口两侧支承螺栓进行有限元分析。

支承螺栓等效应力云图如图11所示。

图11 支承螺栓等效应力云图

由图11可见,该螺栓根部受到较大应力,在其根部的较小区域内出现应力集中现象。

笔者定义最大应力点与支柱螺栓平行方向所在直线为研究对象,分析该直线上等效应力分布情况。

该截面等效应力曲线如图12所示。

图12 支承螺栓垂直截面边缘等效应力曲线

由图12可知,该截面边缘上最大应力值为805.98 MPa,位于支承螺栓根部。

笔者以最大应力点所在圆截面边缘为研究对象,以该点为起点,分析该圆截面边缘上应力分布情况。

该截面边缘等效应力曲线如图13所示。

图13 支承螺栓根部截面边缘等效应力曲线

图13结果显示:该截面应力从89.569 MPa急剧增至805.98 MPa;该支承螺栓所用材料的抗拉强度为985 MPa,屈服强度极限为835 MPa。

从图10、图11中可以看出:最大等效应力值与屈服强度极限非常接近。

通过计算可得,该支承螺栓的安全系数仅为1.036,与安全系数标准1.8存在较大差距[21,22]。

根据实际情况,笔者采用相同方法对销轴进行有限元分析,其等效应力云图如图14所示。

图14 销轴等效应力云图

由图14可知:销轴所受最大应力为484.91 MPa,最大应力出现在销轴孔的边缘处。

笔者以销轴上最大应力点所在水平直线为研究对象,分析该直线上等效应力分布情况。

销轴水平截面边缘等效应力曲线如图15所示。

图15 销轴水平截面边缘等效应力曲线

图15中:销轴两侧边缘处应力极小，几乎为零,在两侧距离边缘点约200 mm左右,出现应力急剧变化现象,且最大应力分布在销轴孔的边缘处。

笔者以销轴孔边缘所在圆截面为研究对象,分析该截面边缘上等效应力分布情况。

该截面边缘等效应力曲线如图16所示。

图16 销轴最大受载截面边缘等效应力曲线

图16分析结果显示:该截面上分布有较大的应力,且保持在约350 MPa～500 MPa之间,其安全系数约为1.722,处于相对安全的状态下。

该厂支承螺栓最大应力已接近其材料35CrMo屈服极限,考虑到倾动加速度及惯性力对支承螺栓冲击力的影响[23],支承螺栓存在较大安全隐患。在长期变工况工作及冲击载荷作用下,易发生螺栓断裂,需对该厂转炉球铰支承装置进行优化设计,以提高其安全系数。

3 改进方案及验证

通过增大螺栓的危险截面尺寸,可大幅度地增加螺栓的强度。该厂原支承螺栓直径为φ280 mm,改进后尺寸为φ290 mm,过度圆弧由R30增至R35,笔者采用相同方法对65°工况进行受力分析。

笔者定义支柱螺栓出现最大应力点为0°点,分析该点所在圆截面上不同角度等效应力大小。

改进后支承螺栓的等效应力对比曲线如图17所示。

图17 支承螺栓改进后等效应力对比曲线

图17分析结果显示:螺栓应力集中现象得到明显改善,应力分布比改进前更加均匀,其最大等效应力值从805.98 MPa降至688.36 MPa,安全系数从1.036提高至1.213,且投入成本降低。

根据上述受力计算分析结果可知:该厂支承螺栓材料35CrMo满足其所需的屈服强度,但在重心偏移,以及长期高温重载工况下,会超出该材质屈服强度的极限值,从而使螺栓根部发生断裂。

支承螺栓常用材料的性能如表2所示。

表2 支承螺栓常用材料性能

根据表2的数据,可选用40CrNiMoV作为支承螺栓材质(该料屈服强度极限值为1 533 MPa,广泛应用于大型机电转子以及大型转炉中),可有效减少极端受力情况下支承螺栓断裂的风险。

4 结束语

针对变工况下转炉支承螺栓的断裂问题,为探明其断裂机理,在不同工况下,笔者对炼钢转炉支承螺栓的断裂机理进行了研究。

笔者首先推导了转炉倾动力矩方程,计算了倾动力矩变化曲线,分析了变工况下转炉支承螺栓的载荷变化规律,探究了倾动角度对支承螺栓受力的影响;以某厂转炉支承螺栓为研究对象,建立了支承螺栓有限元模型。

研究结论如下:

(1)倾动角度为65°时,出钢口对侧支承螺栓过度圆弧处出现危险截面,该截面应力从89.569 MPa急剧增至805.98 MPa,接近所用材料的屈服极限,即在测温、取样、出渣及出钢工况下,可能发生支承螺栓断裂现象;

(2)销轴两侧距离边缘点约200 mm左右位置出现应力急剧变化现象,而最大等效应力未超过500 MPa,处于相对安全状态;

(3)基于转炉承受载荷与角度的关系,笔者提出了转炉支承螺栓有限元模型,模型分析结果表明,最大应力处与实际断裂处一致,说明构建支承螺栓有限元模型的方法是合理的。

在后续的研究工作中,笔者将进一步考虑转炉启动、制动、碰撞过程中产生的冲击负荷,以及环境热应力、惯性力、惯性力矩等对支承螺栓受力的影响,从而为支承螺栓材料的选择及结构的优化设计提供数据参考。