刚性球体三维入水冲击数值仿真

孟 龙， 万美慧， 肖京平

(中国空气动力研究与发展中心， 四川 绵阳 621000)

0 引 言

水上飞机和宇宙飞船的水上降落、太空舱溅落至海洋中等情况均属于结构物入水冲击问题，结构物的入水冲击过程持续时间非常短，瞬时砰击压力大，流体呈现较强的弹性效应，并产生振动[1]，流固耦合作用复杂，有些流动机理尚待研究。

早在1897年WORTHINGTON等[2]就开始入水问题的研究，采用拍摄技术对外形为圆形的结构物进行入水界面处的拍摄，对水气界面处的液滴飞溅和液面闭合情况进行细致的研究。VON KARMAN[3]对入水问题进行系统的理论研究，但是并没有考虑流体的堆积效应。WAGNER[4]基于势流理论提出近似平板理论，该理论适用于小斜升角并且考虑结构物入水时引起的堆积效应，奠定了后续入水问题理论研究和数值模型的基础，然而该理论仍需要引进修正系数进行精确计算[5]。国内众多学者[6-7]也开展大量的结构物入水数值研究，马林[8]主要采用光滑粒子流体动力学(Smoothed Particle Hydrodynamics，SPH)方法开展结构物入水问题的研究，但是其建立的SPH模型对于三维入水问题的使用性较差，对计算资源要求较高，计算时间较长。

随着数值方法(如有限差分法[9-10]、边界元法[11-12]、有限元法[13-14]等)的发展及其在流体流动问题上的应用，对于结构物入水冲击载荷的试验研究[15]也迅速发展起来：张岳青等[16]开展楔形结构物入水问题的研究，主要研究结构物在入水瞬间砰击时的运动响应，对于其他入水砰击问题具有一定的指导作用；ALAOUIA等[17]与张岳青等研究相似，但是两者研究的结构物外形不同，ALAOUIA等主要研究金字塔形状结构物入水瞬时的砰击问题；SHAMS等[18]对入水结构体在外形不对称情况下开展入水砰击研究，并且进行入水参数对载荷影响分析；CHUANG等[19-24]开展平板、楔形体、圆锥体和船模等的入水试验，得出砰击压力的回归经验公式；佘文轩等[25]开展垂直入水砰击试验，主要观察宏观运动响应和细节流场结构；朱贵勋[26]运用多相流模型模拟两相入水砰击问题，但是其研究主要应用于二维，对于三维情况还需要进行改进。

对于结构体入水问题，大部分研究仅进行定性分析，并未给出定量的关系式。本文对不同尺度模型的数值仿真进行系统规划与研究，基于CFD方法开展球体入水冲击载荷特性研究。在不同入水速度、入水角度等参数下进行结构体入水冲击研究，分析模型在不同参数条件下的入水冲击载荷特性问题，进一步揭示流固耦合问题的复杂机理。

1 结构体-流体数值仿真模型计算工况及模型验证

1.1 数值仿真模型

在三维结构物入水冲击数值仿真中，采用笛卡尔坐标系，x轴正方向水平向右，y轴正方向指向图1内部并与x轴形成右手螺旋定则，z轴正方向垂直向上，坐标原点选在平均水线面处，结构体入水冲击示例如图1所示，其中：H为刚性球体距离水平面的高度；h为刚性球体底部距离上方水平面的高度；R为刚性球体半径；r为刚性球体入水某时刻触水半径。刚性球体以一定的初速度和角度入水，入水角度为结构体与水平面之间的锐角夹角，图1中入水角度为90°。

采用商业CFD软件和重叠网格技术开展数值仿真研究，建立多个数值仿真模型，如表1所示，质量为2 370～8 000 g，球体半径为0.06～0.30 m。球体数值仿真模型简化为刚体，具有六自由度运动特性，可在x、y、z等3个方向上进行平动和转动。流体域分为上部空气域和下部水域，在整个计算域中有4种边界条件：速度进口边界、压力出口边界、对称边界和壁面边界。刚性球体在入水砰击过程中会导致自由液面产生较大变化，自由液面的变化同时也会对刚性球体产生重要影响，为了更加精确地得到模型入水时刻的冲击载荷特性，在自由液面附近进行网格加密，同时也对仿真模型进行加密处理。

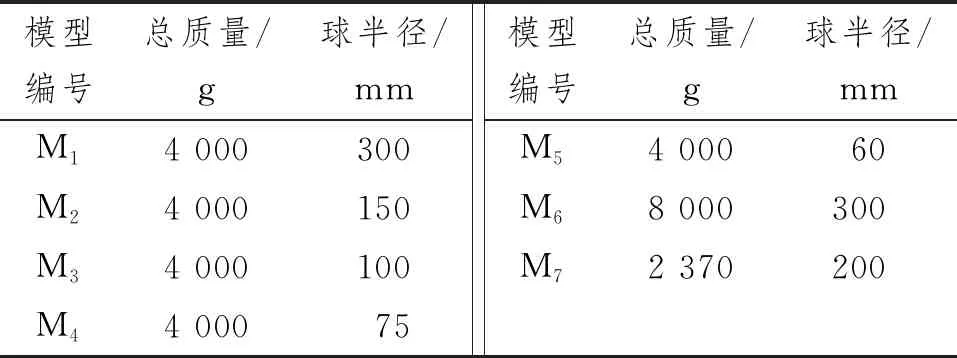
表1 数值仿真模型

为消除网格密度对仿真结果的影响，采用网格密度分别为505万个、755万个和913万个网格开展网格无关性验证。随着网格密度的增大，计算结果呈减小趋势，后两者网格仿真结果的误差为3.78%，但是计算量显著增大。综合考虑，选取网格数量为755万个的网格开展数值仿真，采用重叠网格技术实现刚体在计算域中的运动，仿真网格情况如图2所示。

图2 仿真网格情况

以某工况为例，模型质量选取4 kg，入水速度为15 m/s，入水角度为90°，仿真获得的球体入水时水面处水体积分数变化如图3所示。

图3 球体入水时水面处水体积分数变化

1.2 控制方程和湍流模型

基于雷诺时均的三维黏性不可压Navier-Stokes方程的连续性方程和动量方程分别为

(1)

(2)

采用剪应力传输模型(Shear Stress Transfer，SST)k-ω湍流模型，该模型结合k-ω模型在近壁区域计算的鲁棒性和精确性等优点与k-ε模型适用于远场计算的优点，其输送方程可写为

(3)

(4)

1.3 重叠网格技术

重叠网格是指在计算域中网格相互重叠在一起进行计算的一种网格方案。激活单元、接收单元和失效单元组成重叠网格技术的3种基本单元，激活单元与接收单元之间的插值如图4所示，背景网格与重叠网格共同组成计算域网格[27]。重叠网格与背景网格重叠边界处选取相同大小的网格，采用线性插值方式进行数据传递。在数值仿真过程中，先进行稳态仿真计算，待运行稳定后，在稳态计算结果基础之上开展非稳态数值仿真研究，其中仿真时间步长选取1×10-6s，采用二阶临时离散。

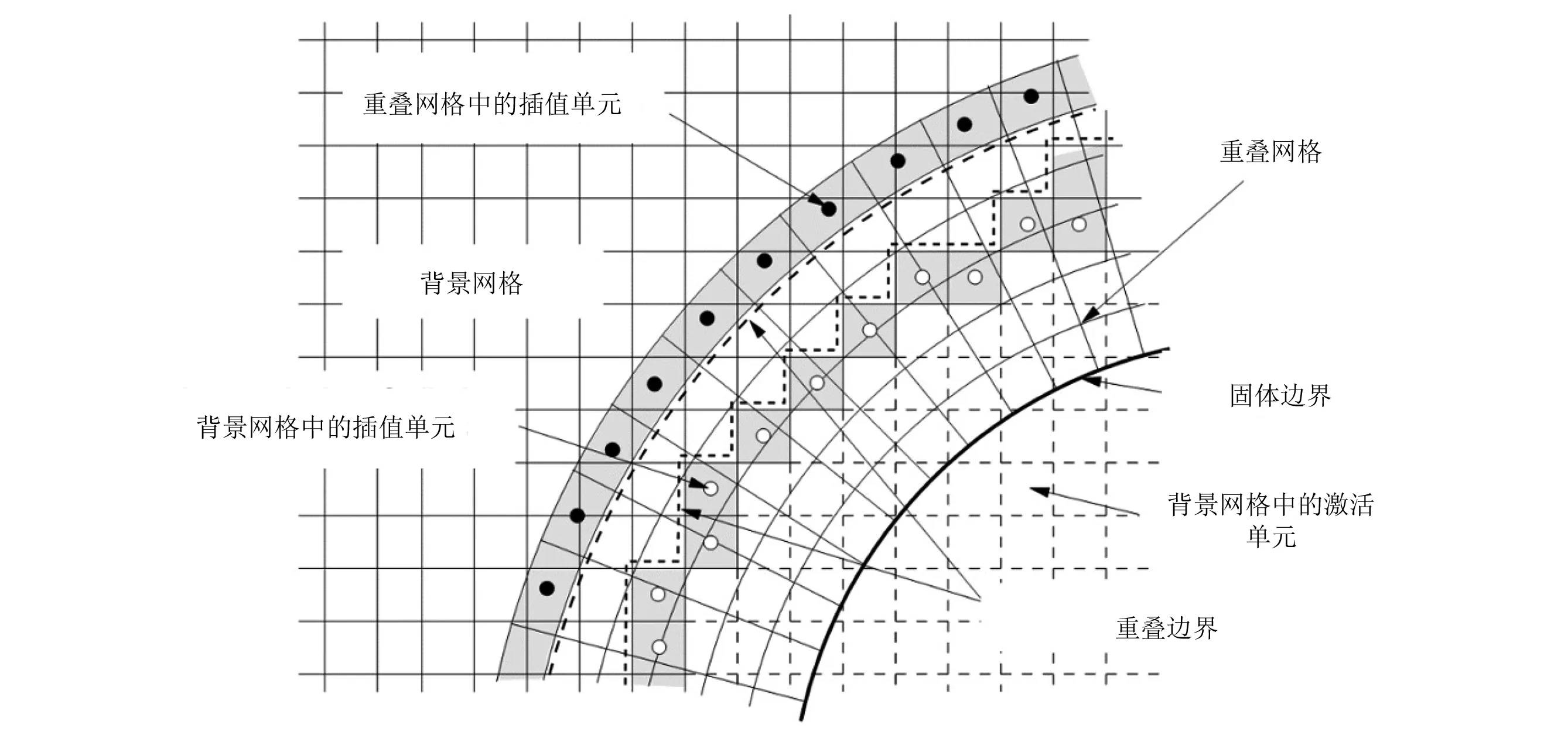
图4 激活单元与接收单元之间的插值

1.4 计算工况和CFD仿真模型验证

采用建立的数值仿真模型，考虑入水速度、入水角度等参数的变化，进行不同工况的数值仿真研究，具体工况如表2所示，其中入水角度为结构体速度方向与平均水线面之间的夹角。根据设计的数值仿真工况，数值仿真主要研究内容如下：

表2 数值仿真工况

(1) 研究结构体入水时不同体积情况下的入水冲击载荷特性。保持结构体质量相同、入水速度相同、入水角度相同，采用5种不同体积的模型，计算工况为LC1～LC5。由于研究球体入水，因此在保证质量相同但是体积不同时，采用空心球模型，通过控制空心球的壁厚来控制球体体积。

(2) 研究结构体入水时不同入水速度情况下的入水冲击载荷特性。采用同一个M1试验模型，保持结构体入水角度相同，改变结构体入水速度，计算工况为LC1、LC6和LC9。

(3) 研究结构体入水时不同入水角度情况下的入水冲击载荷特性。采用同一个M1试验模型，保持结构体入水速度相同，采用多种不同入水角度，计算工况为LC10～LC15。

(4) 研究缩尺模型的缩尺效应对结构体入水冲击载荷的影响。保持结构体入水角度相同，质量、头部直径和入水速度按照缩尺比进行试验，计算工况为LC7和LC8。此时采用的缩尺比为传统海洋工程使用的缩尺法则，具体推导公式可参照文献[28]。

采用CFD方法和文献[29]中的理论计算方法进行球体半径分别为0.10 m、0.15 m和0.30 m的入水过程比较，其中球体质量为4 kg、入水角度为90°。2种方法得出的冲击载荷峰值如表3所示。

表3 数值仿真与理论计算结果比较

随着球体半径的增大，数值仿真结果较理论计算值偏大。在理论计算中，理论模型未考虑结构体入水冲击过程中产生的水堆，水堆的出现使球体周围等效水面抬升，导致入水冲击载荷峰值减小。对于小体积球体，数值仿真与理论计算误差较小，说明所建立的结构体-流体数值仿真模型计算结果具有一定的可信度，可用于后续研究。

2 参数影响分析

采用控制变量法进行参数影响分析，主要分析不同刚性球体体积、不同入水速度、不同入水角度等参数对刚性球体入水冲击载荷特性的影响。对于变体积工况，在保证质量相同的情况下采用空心球模型。

2.1 体积参数影响

在球体质量、入水速度和入水角度相同的情况下，采用中空球体，改变球体壁厚以此改变球体半径，得到冲击载荷随着球体体积变化的规律如图5所示。

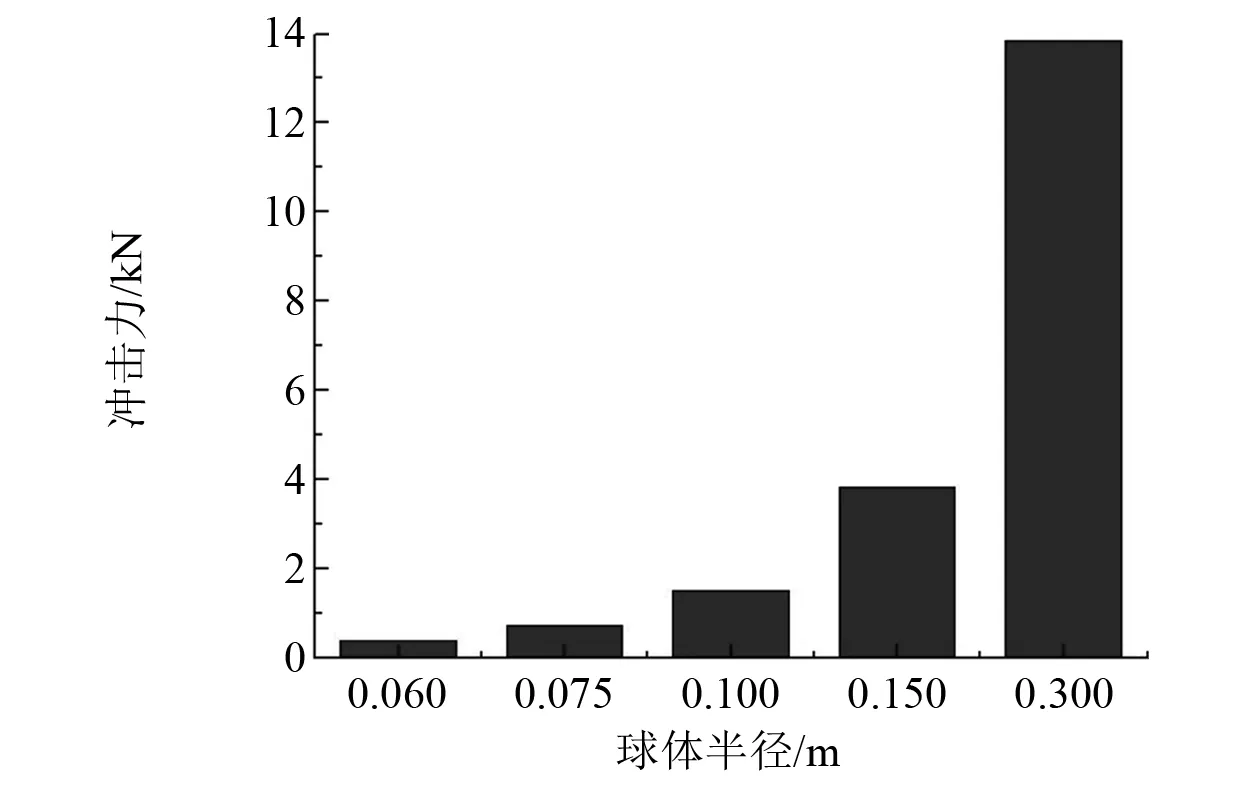
图5 冲击载荷峰值随球体体积变化的规律

球体体积越大，所受到的冲击载荷越大，冲击载荷与球体半径的关系近似为

F=ARα+BRβ+CRγ+D

(5)

式中：F为球体入水冲击载荷峰值；R为球体半径，取值范围为0.06～0.30 m。对模拟数据进行数据拟合，得到如表4所示的参数。

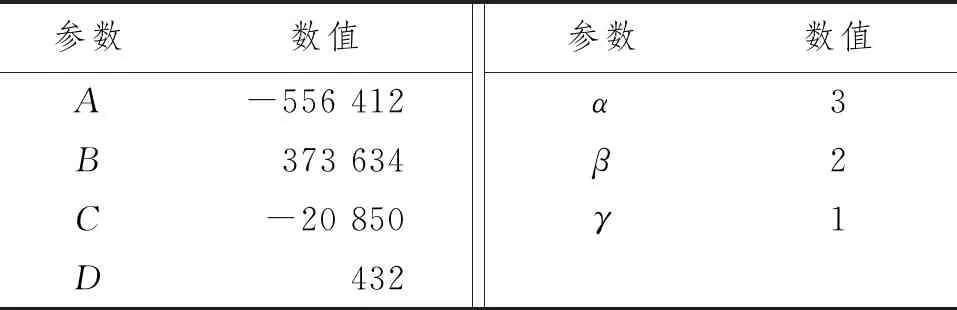
表4 体积参数影响下的数据拟合参数

根据数值仿真结果，当2个体积不同的模型进行入水冲击试验时，若球体半径满足式(6)，则2个模型入水冲击载荷峰值满足式(7)：

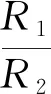
(6)

(7)

式(6)和式(7)中：λR为几何缩尺比。

2.2 入水速度参数影响

在球体质量、球体体积和入水角度相同的情况下，改变入水速度，得到冲击载荷随入水速度变化的规律如图6所示，不同入水速度结构体冲击特性曲线对比如图7所示，入水速度越大，所受到的冲击载荷越大，但是入水冲击载荷的峰值持续时间会缩短。对模拟数据进行拟合，冲击载荷与入水速度的关系近似为

图6 冲击载荷峰值随球体入水速度变化的规律

图7 不同入水速度结构体冲击特性曲线对比

F=11.621v2+27.851v+1 486.5

(8)

式中：v为球体入水速度，取值范围为15～30 m/s。

根据数值仿真结果，当2个入水速度不同的模型进行入水冲击试验时，若入水速度满足式(9)，则2个模型入水冲击载荷峰值满足式(10)：

(9)

(10)

2.3 入水角度参数影响

在球体质量、球体体积和入水速度相同的情况下，改变入水角度，得到冲击载荷随入水角度变化的规律如图8所示，不同入水角度结构体冲击特性曲线对比如图9所示。入水角度越大，所受到的冲击载荷越大。对模拟数据进行拟合，冲击载荷与入水角度的关系近似为

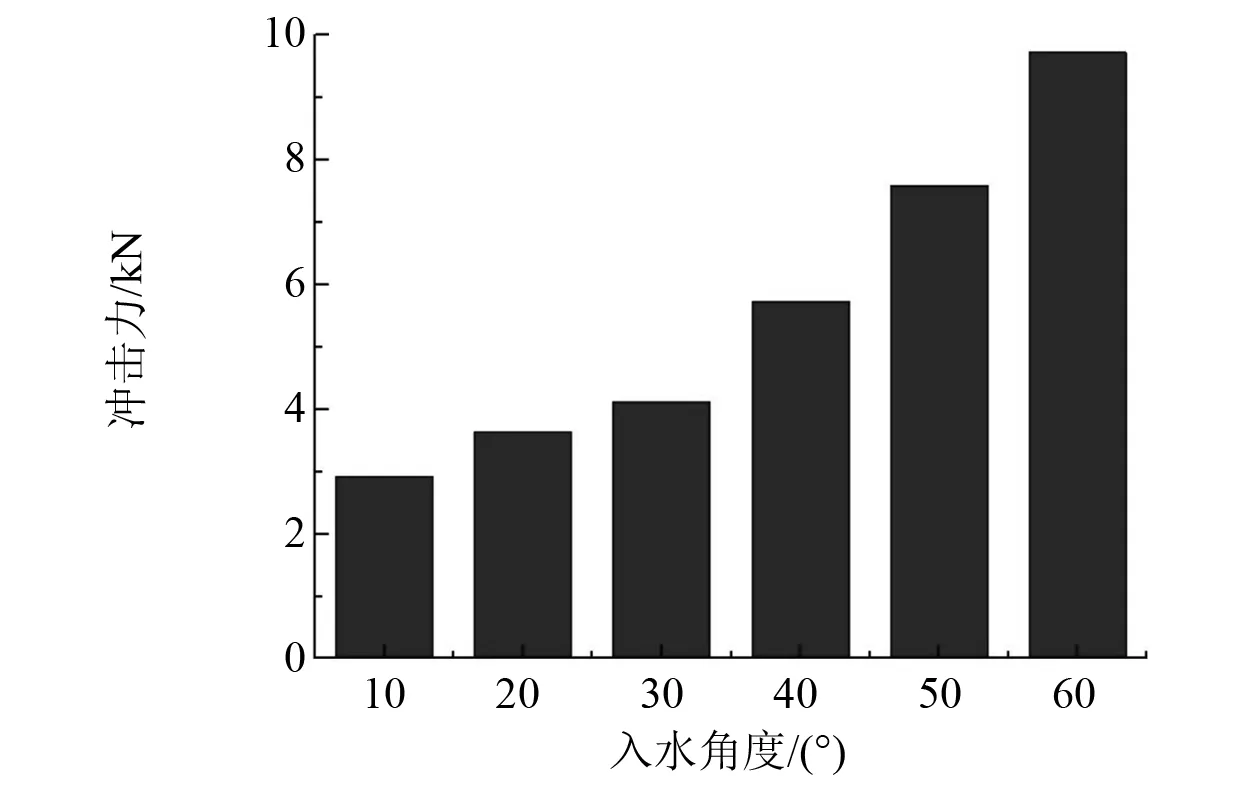
图8 冲击载荷峰值随球体入水角度变化的规律

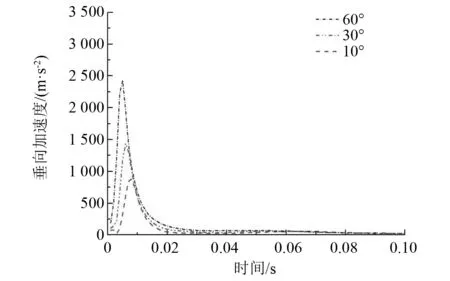
图9 不同入水角度结构体冲击特性曲线对比

F=0.000 3θ5-0.049 1θ4+3.413 6θ3-107.07θ2+1 547.8θ-4 791.3

(11)

式中：θ为球体入水角度，取值范围为10°～60°。

根据数值仿真结果，当2个入水角度不同的模型进行入水冲击试验时，若入水角度满足式(12)，则2个模型入水冲击载荷峰值满足式(13)：

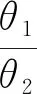
(12)

(13)

2.4 质量速度耦合影响

采用中空的刚性球体，在球体体积不变的情况下，改变球体壁厚以控制球体的质量。在球体体积、入水角度相同但球体的质量和入水速度不相同的情况下，对模拟数据进行拟合，球体所受到的冲击载荷与球体质量和入水速度的关系近似为

(14)

式中：λm和λv分别为质量缩尺比和速度缩尺比。

2.5 缩尺比影响

在保证球体入水角度相同的情况下，球体质量、体积、入水速度按照缩尺法则进行参数设计，几何缩尺比为λL，如式(15)和式(16)所示，根据数值仿真结果，球体所受到的冲击载荷满足式(17)：

(15)

(16)

(17)

3 结 论

基于计算流体力学方法建立结构体高速入水仿真模型，并且与参考文献中理论计算方法进行对比，验证该仿真方法的有效性。在该有效的仿真模型中，比较不同体积、不同入水速度和不同入水角度等参数，得到不同参数对结构物入水冲击载荷特性的影响规律，主要结论如下：

(1) 将所建立的计算流体力学仿真模型与参考文献中理论模型进行比较，入水冲击载荷峰值误差随着球体半径的增大呈现增大的趋势，但是对于小体积结构物两者吻合性较好，建立的仿真模型具有可信度，可用于后续研究。

(2) 入水冲击载荷峰值在结构体入水初期达到最大值，呈现出先增大后减小的趋势。

(3) 采用控制变量法，得到刚性结构体入水冲击载荷峰值在一定范围内与结构体入水速度、入水角度和结构体体积等参数之间的定量关系，得出计算公式并且给出计算公式适用的范围，该计算公式是从模型数据计算出实型数据的计算法则，有利于结构体的初始设计。

建立一种计算结构体高速入水载荷的CFD仿真方法，并为物理试验提供指导，缩短开发周期，具有一定的理论意义和工程应用价值。