基于参考点位移边界条件的千斤顶卸载及顶升模拟方法

焦常科

上海建工集团股份有限公司 上海 200080

千斤顶广泛应用于大跨空间结构或者结构体系转换时的顶升或卸载[1]中。在有限元计算模型中，等效模拟需要实现的特性包括：千斤顶的位移变形特性，千斤顶下的临时支撑结构回弹或进一步压缩，千斤顶与结构支承点脱开或再接触。千斤顶在有限元计算模型中，常见的处理方法包括：将临时支撑及千斤顶简化为支座，对支座分阶段施加强制位移[2]；等效杆端位移法是将临时支撑等效为具有相同轴向线刚度的弹性杆，采用只能受压单元来模拟弹性杆，通过给弹性杆下端支座施加竖向强迫位移来模拟千斤顶的下降[3]；千斤顶单元法，将主体结构与临时支撑同时建在模型中，并在两者之间采用只压单元来模拟真实的千斤顶，将千斤顶单元的轴向刚度设为无穷大，采用施加温度荷载的方法控制千斤顶单元的轴向变形[4]。

蒋金生等[5]基于Ansys平台采用强制位移法对上海新国际博览中心钢桁架结构卸载过程进行分析，计算结果与实测值除局部点最大偏差21%外，其余吻合较好。

常乐等[6]在对跨度120 m的大同美术馆钢结构屋盖施工卸载模拟时，同步与非同步竖向卸载分别采用强制位移和删除支撑胎架实现。

本文从广义约束方程出发，通过引入参考点的边界条件实现千斤顶的顶升或卸载特性。以悬臂梁端部的卸载和顶升为例，将计算结果与理论值进行对比，以说明本文所述方法的正确性。

1 基本原理

有限元模型边界条件处理时，经常会使用耦合方程以在实现若干节点的某些自由度之间形成选定的约束关系，约束方程一般格式如式（1）所示。

在千斤顶上端设置只受压单元模拟千斤顶与结构支承点脱开或再接触特性，千斤顶卸载或顶升的模拟等效示意如图1所示。

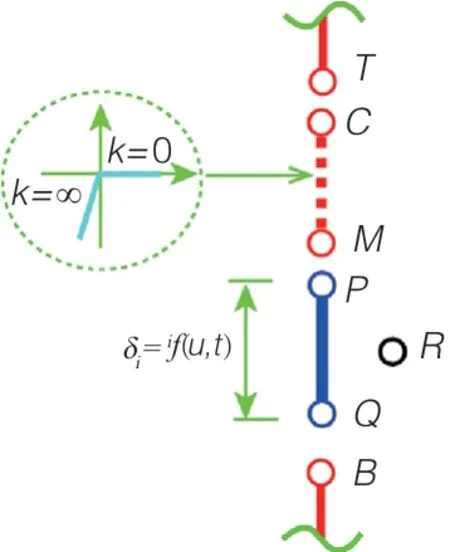
图1 千斤顶等效示意

上述方法可以通过参考点的反力获得千斤顶在进行位移调整过程中的内力变化。基本思路如下：

1）选定千斤顶轴线所在方向，记为z方向，对应的节点自由度为3。

2）假定被支承结构的支承点以及临时支撑点分别为T和B。

3）假定千斤顶的顶、底位置对应的节点分别为P和Q，引入参照节点为R。

4）建立只受压单元，分别连接第1节点C和第2节点M，该单元仅在选定方向z进行力与位移的传递；该单元的抗拉刚度为0，受压刚度为最大值。

5）被支承结构支承点T与只受压单元的第1节点C仅在选定方向z上进行力与位移的传递；千斤顶的顶面对应节点P与只受压单元的第2节点M仅在选定方向z上进行力与位移的传递；千斤顶的底面对应节点Q与临时支撑点B仅在选定方向z上进行力与位移的传递。

6）在节点P、Q和R之间，建立如式（3）所示的约束方程：

7）假定千斤顶的顶、底面对应的节点P和Q，在选定方向z上需产生的相对位移为f(u,t)；对参考节点R在方向z上施加位移边界，对应值为f(u,t)；同时，R节点其他自由度设置固定约束，避免节点R在该自由度上出现刚体位移。

2 单点支撑卸载

以端部设有弹性支承的悬臂梁在均布荷载作用下的力学特性为例，说明温度调节法的基本应用。

悬臂梁为a×b的矩形截面，长L，弹性模量为E；临时支撑长度为l，圆形截面直径为D，弹性模量同悬臂梁，如图2所示。

图2 悬臂梁基本模型

根据力学方法计算得到悬臂梁端部支撑的内力如式（4）所示，相应的端部变形如式（5）所示。

悬臂梁无端部支撑时的竖向位移如式（6）所示，惯性矩的计算如式（7）所示。

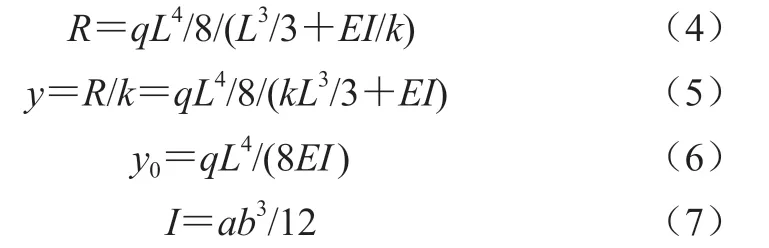
式中：k—悬臂梁端部支撑线刚度，k＝EA/l＝πD2E/(4l)。

选定基本参数值具体如下：E＝2.1×105MPa，a＝50 mm，b＝100 mm，L＝2 m，l＝800 mm，D＝8 mm，q＝20 N/mm。经计算，悬臂梁端部位移及支撑内力分别为y＝－1.109 mm、R＝14.636 kN，相应的固定端竖向反力为25.346 kN；相应无端部支撑时，y0＝45.71 mm。可见：端部支持如完全卸载，临时支撑结构弹性回弹量为1.109 mm；端部卸载量达到45.71 mm时，可达到完全卸载状态。

作为对比，采用温度调节法，将千斤顶等效为弹性模量极大的单个构件，对其施加负温度荷载以达到卸载的目的。将临时支撑上端千斤顶等效为直径6 mm、长100 mm的圆柱，假定其弹性模量E＝2.1×107MPa、线膨胀系数α＝0.01，则对应的温度变化量为ΔT＝－45.71 ℃。

建立平面有限元分析模型，分析步包括：均载q作用；温度调节法中，千斤顶等效单元降温ΔT＝－45.71 ℃，参考点位移法中，对参考点施加竖向位移－45.71 mm；温度调节法中，千斤顶等效单元降温ΔT＝－50.0 ℃，参考点位移法中，对参考点施加竖向位移至－50 mm。

计算结果对比如图3所示。

图3 悬臂梁结构卸载响应

由图3可见，2种模拟方法的结果基本完全一致：在step1中，梁端位移即临时支撑压缩弹性变形为－1.113 mm，与理论值（－1.109 mm）偏差仅0.34%，如图3（a）所示；相应的临时支撑内力计算值为14.54 kN，与理论值（14.636 kN）偏差仅0.66%，如图3（b）所示；在step2中，梁端位移计算值为－45.75 mm，与理论值（－45.71 mm）偏差仅0.09%；相应的临时支撑的压缩变形完全回弹至0，反力全部释放，如图3（c）、图3（d）所示；在step3中，千斤顶继续卸载并与梁端脱开，此时悬臂梁端部位移固定为－45.75 mm，只受压单元进入受拉阶段，相应的临时支撑反力为0，悬臂梁固定端竖向反力维持极值（40 kN）不变，如图3（a）、图3（b）所示。

3 单点支撑顶升

根据悬臂梁端部受集中荷载下的挠度公式，悬臂端部发生位移y时，相应的集中力如式（8）所示。

在上述算例基础上，调整分析步为：均载q作用；对参考点施加竖向位移25 mm；对参考点施加竖向位移至50 mm。计算结果如图4所示。

图4 悬臂梁顶升响应

由图4可见：在step1中，悬臂梁端部挠度及临时支撑反力和固定端反力与理论计算一致；在step2中，千斤顶的上下端面发生25 mm的伸长变形，临时支撑发生0.606 mm（1.719－1.113＝0.606 mm）压缩变形；千斤顶上端及悬臂梁端变形增量为24.293 mm（23.28＋1.113＝24.293 mm），相应临时支撑轴力增量为7.993 kN（22.684－14.691＝7.993 kN），与悬臂梁固定端反力减少量7.933 kN（25.309－17.316＝7.933 kN）吻合，与按式（8）的理论计算结果（8.004 kN）一致；在step3中，千斤顶的上下端面伸长变形继续增大至50 mm，临时支撑总的压缩变形增加至－2.325 mm，悬臂梁端变形增至47.675 mm；相应的悬臂梁固定端反力继续减少，荷载转移至临时支撑上。

由上述分析可见，本文所述模拟方法可准确实现千斤顶的顶升过程模拟。

4 结语

本文从广义约束方程出发，通过引入参考点的边界条件实现千斤顶的顶升或卸载特性。以悬臂梁端部的卸载和顶升为例，将计算结果与理论值对比以说明本文所述方法的正确性。计算结果与理论值对比表明，本方法可真实再现千斤顶的卸载及顶升特性，可在有限元模型建模过程中用于对千斤顶特性进行模拟。