基于NMF和短时能量特征提取的咳嗽识别研究

李 越,徐文龙

(中国计量大学 信息工程学院,浙江 杭州 310018)

咳嗽是一系列呼吸道系统疾病的常见症状,在疾病诊断方面具有重要的临床价值[1]。常见的呼吸道疾病有支气管炎、肺炎、哮喘和百日咳等。咳嗽作为这些疾病的初始症状,通过这一特征表现,在某种程度上能够反映出患者的疾病类型和严重程度,更为客观且方便地辅助医生进行疾病筛查和诊断[2]。

咳嗽声学特性可描述为呼吸道系统的状态。咳嗽声的自动识别和分类,主要借鉴语音识别方面的技术与研究。此外,一些硬件设备比如便携式咳嗽监测仪的出现提高了咳嗽识别的及时性和有效性[3]。

目前,咳嗽声的识别主要通过机器学习的方法,如隐马尔科夫、分类树等模型来实现[4]。此外,深层模型相对于传统模板匹配和浅层神经网络有很大程度的提高。有效的特征提取方法是实现高准确度咳嗽识别的重要因素,研究者一般采取梅尔频率倒谱系数(Mel frequency cepstrum coefficient, MFCC)方法进行咳嗽自动识别和计数。Swarnkarv等[5]选取MFCC、峰度系数、过零率三者结合的特征提取方式,以Logistic作为分类模型,最终完成儿科患者干湿咳声音分类;Matos等[6]通过咳嗽数据训练HMM模型来检测咳嗽音信号,识别准确提升到了82%;Justice等[7]通过训练卷积神经网络(convolutional neural network, CNN)和递归神经网络(recursive neural network, RNN)完成高精度咳嗽信号的检测;MITTAL等[8]则通过评估各类声学特征,使用支持向量机进行咳嗽检测,获得了更好的识别性能。

咳嗽识别方法大多数是在小样本数据集下完成测试的,高准确度的研究方法还在进一步研究当中[9]。采用传统的特征提取方法往往可能会使提取到的特征参数缺乏良好的区分性,从而导致效果并不理想[10]。针对此问题,本文提出一种基于非负矩阵分解(nonnegative matrix factorization, NMF)的特征提取方法,在维数简约的前提下减少了模型训练时间。此外,在设计的咳嗽数据集上,提取咳嗽信号的短时能量特征,将两者的组合参数作为输入特征,通过多种评估指标来反映不同特征提取方式的识别性能。考虑到部分数据的不平衡性,模型方面构建非线性SVM分类器来实现咳嗽信号和非咳嗽信号的自动分类。

1 非负矩阵分解

在语音信号处理中,非负矩阵分解常用于对信号的频谱进行分解。咳嗽信号的频域特征由短时傅里叶变换得到[11],将一个大矩阵分解为几个较小矩阵。分解后的矩阵通常会包含正负元素,但在图像等矩阵中负值元素会使得特征值没有意义。因此,NMF矩阵分解后的非负元素更有利于探索咳嗽的内在特征且具有现实意义。

1.1 非负矩阵分解原理

NMF算法的基本思想可以简单描述为:对于任意给定的一个非负矩阵A,能够找到一个非负矩阵W和一个非负矩阵H,从而将一个非负矩阵分解为左右两个矩阵的乘积,满足条件A=WH,即

Am×n=Wm×rHr×n。

(1)

其中,W为m×r维矩阵,称为基向量矩阵;H为r×n维矩阵,称为系数矩阵;r代表基向量数。

式中,矩阵A表示为咳嗽信号经过短时傅里叶变换后的幅度谱或功率谱组成的信息矩阵,本文选取功率谱矩阵。m和n分别表示信号的频点和时间帧。

非负矩阵分解使分解后的所有分量均为非负值(要求纯加性的描述),同时实现非线性的维数约减。输入特征参数的维数过高,会导致咳嗽识别模型训练过长和内存资源大等问题[12]。该分解算法能够实现特征参数的降维处理,用分解后的系数矩阵H代替原始矩阵,有效提取咳嗽声信号的局部特征,从而改善分类器的各项性能,大大节省计算机的存储空间。

1.2 优化求解

非负矩阵分解算法可以理解为一个优化问题,目的是最小化矩阵W、矩阵H间乘积与原始矩阵A的差异。利用迭代的方法不断优化矩阵A、矩阵W和矩阵H欧氏距离的平方,从而使得乘积矩阵尽可能地接近原始矩阵。目标函数可以表示为

‖A-WH‖2=∑(Aij-(WH)ij)2。

(2)

由目标函数式(2)可知,当A-WH有且为0时,min(A-WH)=0,此时为式子的最优解。

对于NMF目标函数的算法优化问题,采用梯度下降法求解,算法过程如下。

Step1:初始化矩阵W和H。

Step2:设置迭代次数上限和误差阈值。

Step3:依据迭代法则更新迭代W和H,直到全部收敛为止。

Step4:迭代结束后,用系数矩阵H代替原始矩阵,实现降维运算。

算法更新迭代公式如式(3)。

(3)

当矩阵达到收敛,误差值达到稳定[13]。此时说明原始矩阵分解成功,算法结束。

2 支持向量机原理

支持向量机在语音识别尤其是针对小样本数据集中表现出优秀的序列建模能力,同样也适用于咳嗽声识别。具体识别原理与方法如下。

SVM作为一种二分类学习模型,其基本模型是定义在特征空间上的最大间隔线性分类器。学习的基本思想是求解能够正确划分训练数据集和几何间隔最大化的分类超平面[14]。假设给定一个训练数据集T,此样本集是线性可分的,所有在这个超平面上的点x均满足

ω·x+b=0。

(4)

当训练样本集为线性可分时,需要引入非负松弛变量εi[15]。将求解的优化超平面转换为凸二次规划问题,并选取合适的的参数C。C的大小用于表示对错误分类的惩罚程度,转化公式如下:

(5)

将二次规划问题转换为求极大值问题,并构造拉格朗日函数来得到分类决策函数如下:

f(x)=sign(w*·x+b*)。

(6)

其中,sign是符号函数,x代表训练样本,b*是训练样本经过训练后的阈值。

对于线性不可分的情况,把实际问题转化为某个高维空间的线性问题,将二维线性不可分样本映射到高维空间中,使得样本点线性可分。方法是通过非线性变换来实现,即用SVM模型中核函数k(x,y)取代x和y的内积。

核函数的选取对咳嗽声的识别效果起关键性作用,目前常用的核函数及其表达式如表1。

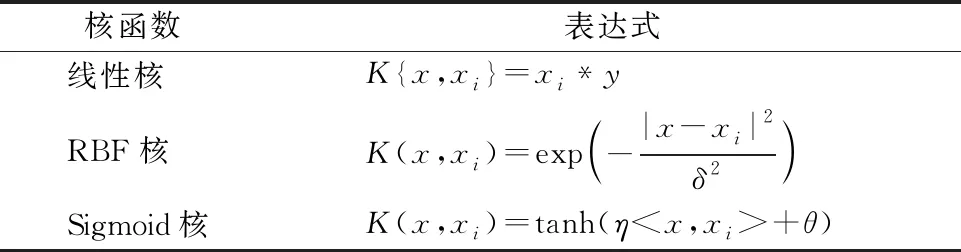
表1 SVM常用核函数

3 实验方法与结果

本文实验数据主要来源于医院门诊和住院部,包含不同呼吸道疾病患者咳嗽录音和各种环境音(哭声、尖叫声)。经过医师和病人同意,使用索尼PCM-D100录音笔对患者咳嗽声进行连续时间的单声道采样,采样频率设为44.1 kHZ。对每个文件的咳嗽类型进行标记,利用Audacity软件截取清晰的咳嗽和非咳嗽片段,将每段音频保存为WAV格式数据,保存在数据库中。最终得到400个咳嗽样本和350个非咳嗽样本。

针对两类数据样本以一定比例划分训练集和测试集,用于后续咳嗽识别实验。随机抽取2/3的数据作为训练样本集,1/3作为测试样本。

本实验大致流程为:首先对咳嗽样本进行预处理操作;再对咳嗽信号和非咳嗽信号进行特征参数提取[16];最后构建SVM分类系统完成咳嗽音自动识别。本文咳嗽识别系统框架如图1。

图1 咳嗽识别系统框架图

3.1 预处理

3.1.1 去噪技术

由于采集的部分咳嗽声包含噪声干扰,需要利用去噪技术消除信号间的一系列噪音,改进语音质量[17]。本研究采用基于小波分解的语音去噪技术,实现多分辨率解析,提高了时域和频域表征局部信息的能力。

信号f(x)的连续小波变换定义如下:

(7)

(8)

其中:参数a为非零实数,称为伸缩因子;b为平移因子。

咳嗽音的小波去噪具体处理过程如下。

首先,将含噪咳嗽声信号在不同尺度下进行小波分解,选择小波分解层次N=6,计算信号每层的分解系数。

其次,从1～N的每一层,设定一个阈值,幅值低于该阈值的小波系数置为0,高于阈值的信号完全保留。

最后,对处理后的小波系数进行重构,根据小波分解的低频系数和修改后的1～N层高频系数,计算咳嗽信号的小波重构。

采用本节小波去噪方法进行实验,去噪后的咳嗽效果如图2。利用此方法有效地去除了咳嗽声以外的噪音干扰,为后续特征提取做准备。

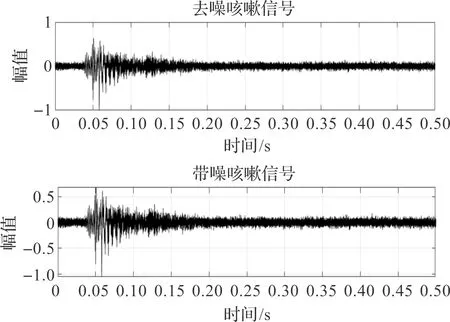
图2 降噪前后效果图Figure 2 Before and after noise reduction renderings

3.1.2 分帧加窗

在短时分析的基础上对咳嗽音进行短时处理。将声音片段分割为帧信号,分割后的每一小段称为一帧,帧长取30 ms。使用交叠分段的方法,使得帧与帧之间平滑连续,前一帧和后一帧的交叠部分为帧移,一般为窗长的1/2[18]。该技术通过窗函数间的平滑移动来实现,本文选取汉明窗,能够避免波形丢失和遗漏现象,反映咳嗽信号间的幅度变化规律。

汉明窗表达式如下:

(9)

3.2 特征提取

3.2.1 NMF特征提取

NMF算法实现了咳嗽信号的频谱分解。通过NMF矩阵分解,一方面将描述咳嗽信号的矩阵维数进行削减,另一方面也可以对大量的数据特征进行压缩和概括,经过预处理后的咳嗽特征具有良好的抗噪性能。从数据样本中划分的训练集和测试集进行实验,测试样本不包含训练样本。

利用所述NMF特征提取方法,对每帧咳嗽信号的特征参数进行提取,特征参数的计算流程如图3。

图3 NMF特征提取流程图

计算过程具体为以下步骤。

步骤1:预处理后的咳嗽信号X(n)通过快速傅里叶变换得到频域数据X(k)。

步骤2:求取谱线能量E(k),计算方法为取模的平方。

步骤3:对能量谱矩阵进行NMF矩阵分解,得到非负基向量矩阵W和系数矩阵H。以系数矩阵H代替原始矩阵,形成所需要的12维特征参数。

3.2.2 短时能量特征提取

短时能量大小可以有效反映信号能量的变化规律且具有代表性。基于咳嗽短暂性、突发性的特点[19],短时能量能够描述音频信号随时间的变化情况。短时能量的计算公式为下式:

(10)

式(10)中,x(m)为输入的咳嗽声信号,ω(n)为所选汉明窗。

图4为咳嗽信号与普通语音信号的短时能量对比图。

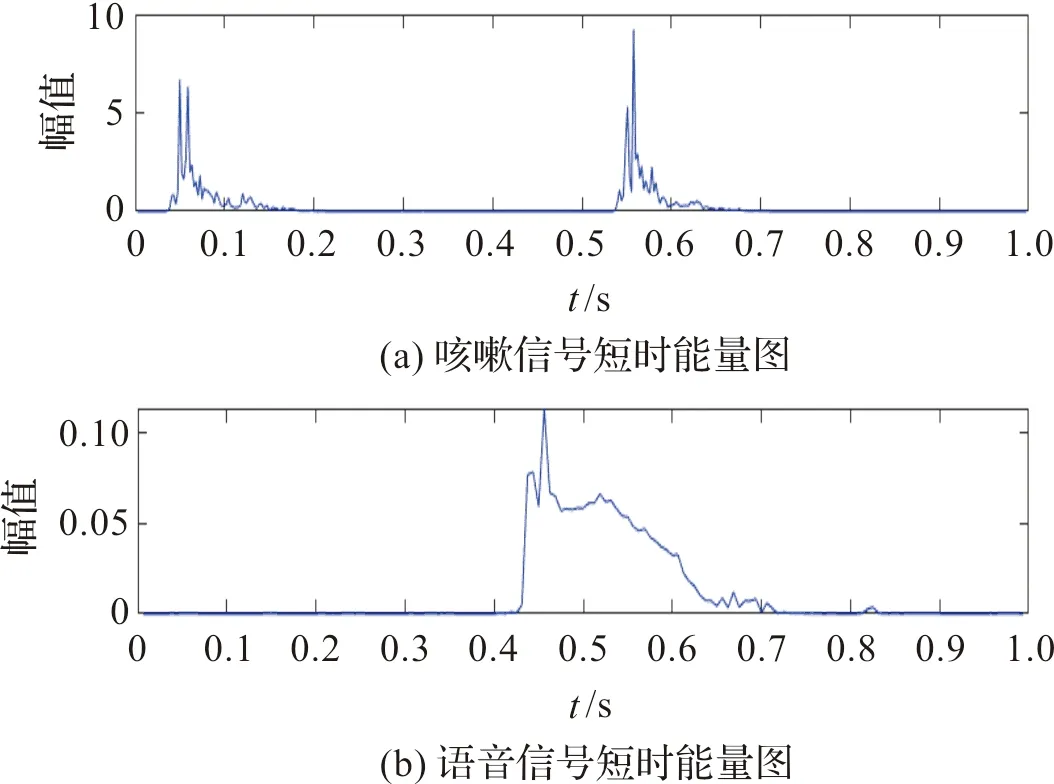
图4 短时能量对比图

3.2.3 特征参数组合

为了构造更有效的咳嗽特征参数,本文提出一种新的特征参数组合方式:将NMF算法分解的咳嗽特征与短时能量进行参数组合作为模型输入。两者组合之后从不同的角度反映了咳嗽音与其他音频信号的特征差异。另外,特征维数方面不会明显增加,运算复杂度大大降低。

实验选取NMF特征参数12维,短时能量特征1维,前后组合连接成13维特征参数。最后将组合的特征参数作为非线性SVM模型的输入进行训练与识别。

3.3 咳嗽分类识别实验

3.3.1 实验环境

实验以pycharm为开发环境,在相同实验条件下,将本文实验结果分别与隐马尔可夫、MLP模型识别结果进行对比。其次,特征提取方面,将本文提出的NMF+E特征组合方式与最新文献方法进行比较实验,以验证本文算法的优越性。

作为对比的隐马尔可夫模型包括3个隐含状态,每个状态包含3个高斯元,通过自左向右的HMM模型实现。采用K均值算法实现高斯混合模型参数初始化,咳嗽训练算法采用Baum-Welch,识别过程则使用Viterbi算法。

多层感知机(MLP)则分别通过输入层、隐藏层和输出层进行咳嗽识别。首先随机初始化所有参数,然后进行迭代训练,计算梯度值并更新参数,直到满足某个条件为止(比如误差足够小、迭代次数足够多)。

3.3.2 实验结果分析

运用本文算法进行咳嗽识别,分类模型采取支持向量机,选用适应性强的径向基核函数,根据实验确定最优参数。训练样本选取150个咳嗽信号和150个非咳嗽信号训练最佳分类模型,测试集选择100个咳嗽信号和130个非咳嗽信号完成测试。实验结果如表2。其中,咳嗽识别准确率=正确识别的咳嗽个数/咳嗽总数×100%,非咳嗽的识别准确率=正确识别的非咳嗽个数/非咳嗽总数×100%。

由表2可知,该分类系统对于咳嗽声的识别率达到93.75%,误识别率仅为7.3%,获得良好的分类效果。本文算法能够准确地将咳嗽音从其它音频信号中分离,反映了算法的可适用性。

表2 识别结果

以咳嗽识别准确率作为指标,得到本文评估曲线如图5。由评估曲线可以看出,采用SVM分类的咳嗽识别准确率和模型可扩展性均表现出较好的效果。因此,SVM分类器在小样本数据集情况下的泛化能力较强[20],能够有效提高系统的性能。

图5 SVM模型性能评估曲线

为验证本文特征提取方法的有效性,将所述NMF+E特征提取算法分别与传统MFCC、MFCC+E进行对比实验。以特异性、灵敏度、准确度作为评估指标,模型均采用非线性SVM,实验结果如图6,其中,特异性=正确识别的非咳嗽声个数/非咳嗽声总数×100%,灵敏度=正确识别的咳嗽声个数/咳嗽声总数×100%。

图6 不同特征参数结果对比

由图6可以看出,四种特征提取方式中,采用本文特征提取算法的实验效果最佳,SVM模型各方面咳嗽识别性能最好,准确度最高达93.75%。相比其他三种特征提取方式,本文咳嗽识别效果更显著,而采用传统MFCC识别效果最低,咳嗽识别准确度仅为83%。由此,采用本文特征组合的方式更能增强特征提取的表达能力。

为了选取咳嗽识别系统的最佳识别算法及其特征组合,我们将采集的咳嗽数据集用于特征选择和模型评估。实验采用五折交叉验证的方法分别使用非线性SVM、隐马尔可夫(HMM)、随机森林(random forest, RF)和多层感知机(multi-Layer perceptron, MLP)四种模型进行咳嗽识别实验。特征参数同样选取不同的方法进行,在测试集上对咳嗽识别性能进行测试,得到如表3所示的评估结果对比。咳嗽识别算法分别选用本文方法、文献[21]、文献[22]和研究者常用的几种参数结合方式,由表3可以看出,非线性SVM模型在特异性、灵敏度、准确度方面都表现出明显的优势。测试集下的咳嗽识别准确度最高达到94.75%,错误率仅为4.9%,相对于HMM、随机森林、MLP等分类模型咳嗽识别性能更为优越,这表明SVM能使数据样本可分性更强。

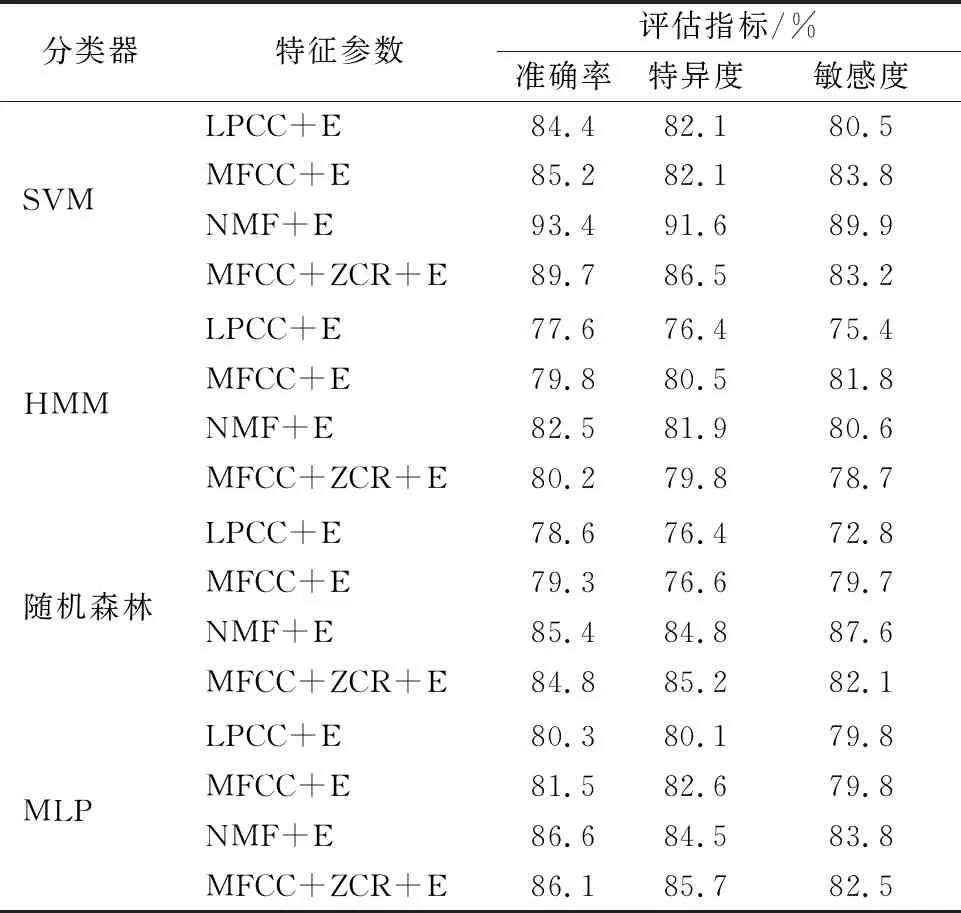
表3 不同算法咳嗽识别结果

将表3不同特征提取算法和模型的咳嗽识别结果进行对比,可以发现,采用本文NMF+E的特征参数组合方法和SVM模型识别效果最突出,准确率达到93.4%。此外,采用MFCC+ZCR+E的特征组合方法识别效果较好,但特征维数较高,而本文识别算法实现了特征向量的降维运算。综上所述,本文咳嗽识别系统能够对咳嗽声进行准确计数和自动识别,从而改善分类器的各项性能。

4 结 语

为了提高咳嗽信号的识别率,本文提出了一种非负矩阵分解(NMF)和短时能量(E)特征参数结合的方法。该识别算法综合考虑了咳嗽音的各方面特性,提取的咳嗽特征更加全面且具有代表性。考虑到咳嗽音识别过程中特征参数维数高的特点,对初始特征矩阵进行降维分解,从而减少系统开销。以特异度、准确度和灵敏度作为衡量指标判别其识别性能,由实验结果可知,采用NMF+E的特征提取算法和传统方法相比效果得到进一步提升,咳嗽识别准确度由89.87%提高到93.75%。下一步的研究重点是进一步扩大咳嗽样本,研究如何更好地消除数据中的噪声干扰,进一步提高特征鲁棒性和模型分类性能。