振动频率对含瓦斯煤渗透特性的影响及模型验证

曹伟伟，温 欣，张晓彬，洪学娣

(唐山工业职业技术学院，河北 唐山 063299)

随着煤炭开采向深部延伸，在煤系地层采掘的过程中将会遇到越来越多的问题和挑战，其中瓦斯气体在煤系地层中的流动运移规律不明确等问题较为突出。为此，专家学者们开展了大量的研究。Somerton等[1]依据三轴压力下的渗流实验结果，推断出地应力是影响煤体渗流的主要因素之一；王汉鹏等[2]依据试验结果总结出煤体内瓦斯的渗流规律与达西定律并不完全相符，并根据试验结论提出更符合实际情况的幂定律；孙培德等[3]建立了适用于均质、非均质煤层内瓦斯气体流动规律的渗流理论；Du等[4]研究发现了煤体骨架与瓦斯渗流之间的作用关系；费玉祥等[5]通过试验总结出渗透率随应力的变化关系，并建立了两者之间的关系动态模型；尹光志等[6]研究了含瓦斯煤渗流特征的变化情况，并探究峰值渗流速度与围压的关系；李培超等[7]引入了有效应力原理，建立了饱和多孔介质流固耦合模型；田卫东等[8]建立了气—水两相双重介质模型；Wu[9]考虑到煤损伤过程中蠕变效应和透气性的改变，建立了考虑损伤的流固耦合模型；杨天鸿[10]、徐涛[11]、刘星光[12]、薛熠[13]等依据损伤力学、断裂力学原理分别建立了考虑损伤效应的应力—损伤—渗流模型。

上述研究主要从定性的角度分析煤与瓦斯突出的相关问题，未能充分考虑低频振动对含瓦斯煤渗透性的影响。笔者通过开展不同振动频率和瓦斯压力下的含瓦斯煤渗透性试验，探究不同振动频率和瓦斯压力下含瓦斯煤的渗透性变化规律，并依据孔隙率公式与对应的应变增量表达式建立孔隙率与渗透率动态演化方程，进而得到考虑振动作用影响的流固耦合模型，再将建立的模型导入有限元软件进行模拟，对比模拟结果与试验结果，以验证模型的可行性。

1 振动频率试验

1.1 试验装置

本次低频机械振动下含瓦斯煤岩渗透试验由自主研发的试验装置完成。试验装置主要由4个部分组成，分别为试验发生装置、压力加载装置、激振装置、监测装置，如图1所示。

1—夹持器；2—激振器；3—发生器；4—高压瓶；5—显示仪；

1.2 试验方案

1.2.1 试样的制作

本次试样取自河北唐山的开滦煤矿，通过切割打磨制成尺寸为ø25 mm×50 mm的原煤试样。部分试样如图2所示。

图2 试样实图

1.2.2 试验步骤

本次试验采用氮气作为气体介质，研究含瓦斯煤在不同围压(2、4、6 MPa)和振动频率(0、10、20、30、40、50 Hz)下的渗透特性，试验中调节瓦斯压力，从0 MPa逐渐增加到2 MPa，每次增幅为0.1 MPa。

具体步骤如下：

1)打开所有进气阀门和压力显示器阀门，向试验腔内充入氦气，检查装置的气密性。

2)将试样放入岩心夹持器内的腔室后，将流量测量装置与高压管线连接好。

3)操作压力水泵缓慢地将轴压与围压加载到2 MPa，待示数稳定后，关闭控制阀门。

4)打开气压加载阀门，将瓦斯压力加载到不同的气压值，分别测量气体流量。瓦斯压力的大小通过控制加载阀门的进气速率来调节，具体数值在压力表中读取。

5)拆卸岩心夹持器一侧的腔室盖，更换试样后重新连接高压管线，启动模态激振器、信号发射器，在5组振动频率下分别振动500 s，每组振动结束后重复步骤4)。

6)在2 MPa的围压试验结束后，更换试件，将围压加载到4、6 MPa，在其他2组压力条件下重复步骤4)、步骤5)，所有压力条件下的试验都操作完毕后试验结束。

1.3 试验结果分析

根据达西定律，瓦斯气体通过煤样试件的渗透率可以表示为[14]：

(1)

式中：K为渗透率,10-3μm2；μ为瓦斯黏度系数；p0为大气压力，MPa；Q1为煤样横截面流速,cm3/s；L为试样长度，m；A为截面面积，m2；p1为煤样进口压力，MPa；p2为煤样出口压力，MPa。

1.3.1 瓦斯压力对渗透率的影响

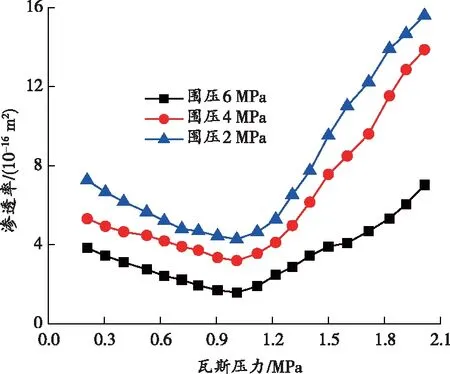
绘制不同振动频率下含瓦斯煤的渗透率随瓦斯压力的变化曲线，如图3所示。

(d)振动频率30 Hz

(e)振动频率40 Hz

(f)振动频率50 Hz

从图3可以看出，在相同振动频率下，渗透率随瓦斯压力的增大呈现出先下降后上升的变化趋势，曲线存在瓦斯压力临界值，并且上升的渗透率增量高于下降的渗透率损失量，瓦斯压力与渗透率的这种“V”形变化关系符合克林伯格效应，本试验的克林伯格瓦斯压力临界点约为1.0 MPa。

1.3.2 振动频率对渗透率的影响

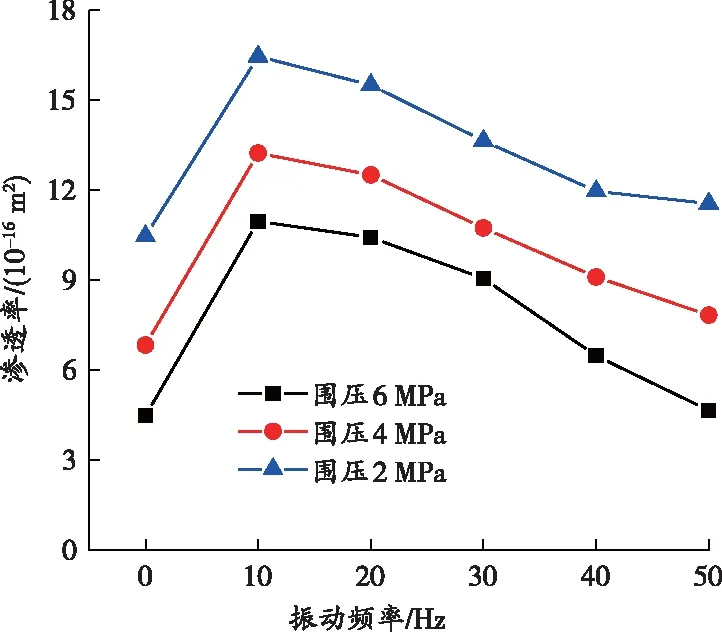
为探究振动频率对含瓦斯煤的渗透性影响规律，绘制不同瓦斯压力下含瓦斯煤的渗透率随振动频率的变化曲线，如图4所示。

(a)瓦斯压力0.5 MPa

(b)瓦斯压力1.0 MPa

(c)瓦斯压力1.5 MPa

(d)瓦斯压力2.0 MPa

从图4可以看出，在振动频率小于10 Hz时，渗透率随振动频率的增大迅速增大，在10 Hz左右达到最大值后，随着振动频率的继续增大，渗透率缓慢减小并最终趋于稳定。原因为含瓦斯煤体内部的结构在振动作用下发生改变，振动使得孔裂隙中原来存在的堵塞物质被清除，孔隙率与渗透率均随之增大，而随着试验的进行，在围压一定的条件下，煤体骨架会受到吸附膨胀作用导致其体积增大，当吸附膨胀应力小于煤体屈服强度时，煤体内部不会产生裂纹，增大的体积反而向内膨胀，导致孔裂隙通道变窄，孔隙率与渗透率随之减小，最终达到稳定。

2 煤系地层孔隙率与渗透率动态演化方程

2.1 孔隙率动态演化方程

从孔隙率的基本定义出发，用孔隙率来表示孔隙与裂隙形成的共同空间，并假设煤体内只有瓦斯一种气体，孔隙率方程可由下式表示[15]：

(2)

式中：φ为煤的孔隙率；VP为孔隙体积，m3；V为煤总体积，m3；ΔVP为孔隙体积变化，m3；ΔV为煤总体积变化，m3；VP0为初始孔隙体积，m3；V0为煤初始总体积，m3；ΔVS为煤骨架体积变化，m3；VS0为煤初始骨架体积，m3；φ0为煤初始孔隙率；εV为煤的体积应变。

煤体骨架体积应变的影响因素[16]：

(3)

式中：ΔVSP为瓦斯压力导致的骨架体积变化，m3；ΔVSF为煤体吸附瓦斯膨胀导致的骨架体积变化，m3；ΔVSQ为挤压作用导致的骨架体积变化，m3。

孔隙压缩应变、吸附膨胀应变表示为[17]：

(4)

式中：ν为泊松比,ν=0.206；E为弹性模量，E=17.62 MPa；Δp为压力增量，MPa；ρs为煤的视密度，kg/m3；R为普式气体常数，R=8.314 J/(mol·K)；a为单位质量煤极限吸附量，m3/kg；b为吸附平衡常数，MPa-1；Vm为气体摩尔体积，Vm=22.4×10-3m3/mol；T为温度，K；p为压力，MPa。

由应力应变关系可得挤压应变如下[18]：

(5)

式中：EV为煤体体积模量，MPa，EV=E/3(1-2ν)；σr为衰减应力，MPa；F0为驱动力，kN；ω为振动频率,Hz；t为时间,s；D0为初始损伤；s为振动源到受振动煤体的距离，m；ms为振动作用s米下的煤体质量，kg；m、n为初始损伤参数，m=0.826 1,n=0.139 3。

煤体骨架应变增量ΔVS/ΔVS0：

(6)

将式(6)代入式(2)可得孔隙率动态演化方程：

(7)

2.2 渗透率动态演化方程

有效应力的作用使煤体骨架产生形变，因此有效体积应力表达式如下[18]：

Θ′=EVεV

(8)

煤体在峰前有效体积应力与渗透率关系[19]：

K=K0exp(-c0Θ′)

(9)

式中：K0为初始渗透率；c0为材料参数。

将式(7)、式(8)代入式(9)可以得到含瓦斯煤渗透率动态演化方程：

(10)

3 数值模型的验证

3.1 几何模型与边界条件

该模型由应力场以及渗流场两场耦合而成，通过Ansys软件中的固体力学模块与PDE模块对耦合方程进行求解[20]。几何模型尺寸为ø25 mm×50 mm的圆柱体，如图5所示。

图5 渗流场和应力场边界

设置温度恒定为28 ℃，模型左右两边进气口和出气口压力分别为2.0 MPa和0.1 MPa，轴压和围压均为4 MPa，振动频率分别设置为10、20、30、40 Hz。

3.2 材料参数与网格划分

所建模型的煤样物性参数如表1所示。

表1 煤样物性参数

将材料参数设置完毕以后，对几何模型进行网格划分，并细化模型左右两侧的网格，如图6(a)所示。在几何模型中选取一个具体的观测点(0，0，25)对其进行分析，具体位置如图6(b)所示。

图6 几何模型网格划分及观测点位置

3.3 试验结果与模拟结果对比分析

将模拟求解得到的结果与试验得到的实测结果进行对比，如图7所示。

图7 试验结果与模拟结果对比

由图7可知，虽然试验结果与模拟结果具有一定的偏差，但是模拟结果能够大致反映试验的发展趋势，而且二者的数据也较为吻合。据此可以说明所建立的数学模型具有合理性。

4 结语

1)在一定振动频率和围压作用下，含瓦斯煤的渗透率随瓦斯压力的增大呈现出先下降后上升的变化规律；在瓦斯压力和围压一定的情况下，含瓦斯煤体的渗透率随振动频率的增加呈现先增大后减小的变化趋势。

2)通过将推导得到的孔隙率与渗透率动态演化方程引入渗流场方程，得到应力场方程，并与渗流场方程及边界条件共同组成了考虑振动作用影响的含瓦斯煤体流固耦合数学模型。

3)将流固耦合模型嵌入Ansys软件中模拟试验过程，与试验数据相对比以后发现，该模拟结果能够反映试验的发展趋势，说明所建立的数学模型具有合理性。